CIELUV

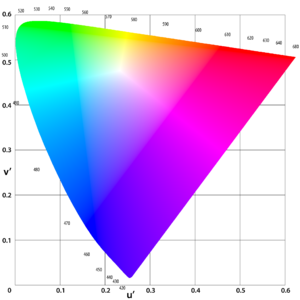
W kolorymetrii przestrzeń barw CIE 1976 L *, u *, v * , powszechnie znana pod skrótem CIELUV , to przestrzeń barw przyjęta przez Międzynarodową Komisję ds. Oświetlenia (CIE) w 1976 r. jako prosta do obliczenia transformacja przestrzeń kolorów CIE XYZ z 1931 roku , ale która próbowała ujednolicić percepcję . Jest szeroko stosowany w aplikacjach takich jak grafika komputerowa, które zajmują się kolorowymi światłami. Chociaż addytywne mieszaniny różnokolorowych świateł będą układać się na linii w jednolitym diagramie chromatyczności CIELUV (zwanym UCS CIE 1976 ), takie addytywne mieszaniny nie będą, wbrew powszechnemu przekonaniu, układać się wzdłuż linii w przestrzeni kolorów CIELUV, chyba że mieszaniny są stałe w lekkości .

Tło historyczne

Gama sRGB ( po lewej ) i widzialna przy oświetleniu D65 ( po prawej ) wykreślona w przestrzeni kolorów CIELUV. u i v to osie poziome; L to oś pionowa.

CIELUV to chromatyczna walencyjna przestrzeń barw Adamsa i jest aktualizacją przestrzeni barw CIE 1964 ( U *, V *, W *) (CIEUVW). Różnice obejmują nieco zmodyfikowaną jasności i zmodyfikowaną jednolitą skalę chromatyczności, w której jedna ze współrzędnych v ′ jest 1,5 razy większa niż v w jej poprzedniku z 1960 r . CIELUV i CIELAB zostały przyjęte przez CIE jednocześnie, kiedy nie można było sformułować jasnego konsensusu za tylko jedną lub drugą z tych dwóch przestrzeni kolorów.

punktu bieli typu Judda (translacyjną) (w przeciwieństwie do CIELAB, który wykorzystuje „niewłaściwą” transformację Kriesa ). Może to dać użyteczne wyniki podczas pracy z pojedynczym źródłem światła, ale może przewidywać wyimaginowane kolory (tj. poza miejscem widmowym ) podczas próby użycia go jako chromatycznej transformacji adaptacyjnej . Wykazano również, że transformacja adaptacji translacyjnej stosowana w CIELUV słabo sprawdza się w przewidywaniu odpowiednich kolorów.

Konwersje XYZ → CIELUV i CIELUV → XYZ

Dla typowych obrazów zakres u * i v * ±100%. Z definicji 0 ≤ L * ≤ 100 % .

Transformacja do przodu

CIELUV opiera się na CIEUVW i jest kolejną próbą zdefiniowania kodowania z jednolitością w postrzeganiu różnic kolorystycznych . Nieliniowe zależności dla L *, u * i v * podano poniżej:

${\ Displaystyle {\ rozpocząć {wyrównane} L ^ {*} & = {\ rozpocząć {przypadki} \ left({\frac {29}{3}}\right)^{3}Y/Y_{n},&Y/Y_{n}\leq \left({\frac {6}{29}}\right) ^{3}\\116\left(Y/Y_{n}\right)^{1/3}-16,&Y/Y_{n}>\left({\frac {6}{29}}\right )^{3}\end{przypadki}}\\u^{*}&=13L^{*}\cdot (u^{\prime}-u_{n}^{\prime})\\v^{ *}&=13L^{*}\cdot (v^{\prime}-v_{n}^{\prime})\end{wyrównane}}}$

Wielkości u ′ _n i v ′ _n to współrzędne chromatyczności ( u ′, v ′) „określonego białego obiektu” - który można nazwać punktem bieli - a Y _n to jego luminancja. W trybie odbicia jest to często (ale nie zawsze) traktowane jako ( u ′, v ′) idealnego dyfuzora odbijającego pod tym źródłem światła. (Na przykład dla obserwatora 2° i standardowego oświetlacza C, u ′ _n = 0,2009 , v ′ _n = 0,4610 .) Równania dla u ′ i v ′ podano poniżej:

${\ Displaystyle { \begin{aligned}u^{\prime }&={\frac {4X}{X+15Y+3Z}}&={\frac {4x}{-2x+12y+3}}\\v^{\ liczba pierwsza }&={\frac {9Y}{X+15Y+3Z}}&={\frac {9y}{-2x+12y+3}}\end{wyrównane}}}$

Odwrotna transformacja

( u ′, v ′) diagram chromatyczności, znany również jako diagram CIE 1976 UCS (jednolita skala chromatyczności).

Transformacja z ( u ′, v ′) do ( x , y ) to:

${\ Displaystyle {\ rozpocząć {wyrównane} x & = {\ Frac {9u ^ {\ pierwsza}} {6u^{\prime}-16v^{\prime}+12}}\\y&={\frac {4v^{\prime}}{6u^{\prime}-16v^{\prime}+12} }\end{wyrównane}}}$

Transformacja z CIELUV do XYZ odbywa się w następujący sposób:

${\ Displaystyle {\ rozpocząć {wyrównane} u ^ {\ pierwsza} &={\frac {u^{*}}{13L^{*}}}+u_{n}^{\prime }\\v^{\prime }&={\frac {v^{*}} {13L^{*}}}+v_{n}^{\prime}\\Y&={\begin{przypadki}Y_{n}\cdot L^{*}\cdot \left({\frac {3} {29}}\right)^{3},&L^{*}\leq 8\\Y_{n}\cdot \left({\frac {L^{*}+16}{116}}\right) ^{3},&L^{*}>8\end{przypadków}}\\X&=Y\cdot {\frac {9u^{\prime}}{4v^{\prime }}}\\Z&=Y \cdot {\frac {12-3u^{\prime}-20v^{\prime}}{4v^{\prime}}}\\\end{wyrównane}}}$

Reprezentacja cylindryczna (CIELCh)

Gama sRGB ( po lewej ) i widzialna gama przy oświetleniu D65 ( po prawej ) wykreślona w przestrzeni kolorów CIELCHuv. L to oś pionowa; C to promień cylindra; h jest kątem wokół obwodu.

Przestrzeń barw CIELCh _uv lub HCL (odcień – chroma – luminancja) jest coraz częściej postrzegana przez społeczność zajmującą się wizualizacją informacji jako pomoc w prezentowaniu danych bez uprzedzeń związanych ze stosowaniem zmiennego nasycenia .

Cylindryczna wersja CIELUV jest znana jako CIELCh _uv lub CIELCchuv, CIELCh(uv) lub CIEHLC uv , gdzie C * _uv to nasycenie , a h _uv to odcień _:

${\ Displaystyle C_ {uv} ^ {*} = \ operatorname {hypot} (u ^ {*} ,v^{*})={\sqrt {(u^{*})^{2}+(v^{*})^{2}}},}$

${\ Displaystyle h_ {uv} = \ nazwa operatora {atan2} (v ^ {*}, u ^ {*}),}$

gdzie funkcja atan2 , „dwuargumentowy arcus tangens”, oblicza kąt biegunowy na podstawie kartezjańskiej pary współrzędnych.

Ponadto korelat nasycenia można zdefiniować jako

${\ Displaystyle s_ {uv} = {\ Frac {C ^ {*}} {L ^ {*}}} = 13 {\ sqrt {(u'-u'_ {n}) ^ {2} + (v '-v'_{n})^{2}}}.}$

Podobne korelaty nasycenia i barwy, ale nie nasycenia, istnieją dla CIELAB. Zobacz Kolorowość , aby uzyskać więcej dyskusji na temat nasycenia.

Różnica koloru i odcienia

Różnicę kolorów można obliczyć za pomocą odległości euklidesowej współrzędnych ( L *, u *, v *) . Wynika z tego, że odległość chromatyczności wynosząca ${\ Displaystyle {\ sqrt {(\ Delta u ') ^ {2} + (\ Delta v') ^ { 2}}}=1/13}$ odpowiada temu samemu Δ E * _uv jak różnica jasności Δ L * = 1 , w bezpośredniej analogii do CIEUVW.

Metrykę euklidesową można również zastosować w CIELCh, przy czym ten składnik Δ E * _uv można przypisać różnicy w odcieniu jako Δ H * = √ C * ₁ C * ₂ 2 sin (Δ h /2) , gdzie Δ h = h ₂ − godz ₁ .

Zobacz też

• YUV
• Przestrzeń barw CIELAB

Linki zewnętrzne

• Diagramy chromatyczności, w tym CIE 1931, CIE 1960, CIE 1976
• Colorlab MATLAB do obliczeń z zakresu nauki o kolorach i dokładnego odtwarzania kolorów (autorzy: Jesus Malo i Maria Jose Luque, Universitat de Valencia). Obejmuje standardową kolorymetrię trójchromatyczną CIE i transformacje do wielu nieliniowych modeli wyglądu kolorów (CIE Lab, CIE CAM itp.).