Przestrzeń barw CIE 1931

Przestrzenie kolorów CIE 1931 są pierwszymi zdefiniowanymi ilościowo powiązaniami między rozkładami długości fal w widzialnym widmie elektromagnetycznym a fizjologicznie postrzeganymi kolorami w widzeniu barwnym przez człowieka . Relacje matematyczne, które definiują te przestrzenie kolorów , są niezbędnymi narzędziami do zarządzania kolorami , ważnymi w przypadku kolorowych atramentów, podświetlanych wyświetlaczy i urządzeń rejestrujących, takich jak aparaty cyfrowe. System został zaprojektowany w 1931 roku przez „Commission Internationale de l'éclairage” , znaną w języku angielskim jako Międzynarodowa Komisja Oświetleniowa .

Przestrzeń kolorów CIE 1931 RGB i przestrzeń kolorów CIE 1931 XYZ zostały stworzone przez Międzynarodową Komisję ds. Oświetlenia (CIE) w 1931 roku. Powstały w wyniku serii eksperymentów przeprowadzonych pod koniec lat dwudziestych XX wieku przez Williama Davida Wrighta przy użyciu dziesięciu obserwatorów i Johna Guilda przy użyciu siedmiu obserwatorzy. Wyniki eksperymentów połączono w specyfikację przestrzeni barw CIE RGB, z której wyprowadzono przestrzeń barw CIE XYZ.

Przestrzenie kolorów CIE 1931 są nadal szeroko stosowane, podobnie jak przestrzeń kolorów CIELUV z 1976 roku .

Wartości trójbodźcowe

Znormalizowana czułość widmowa ludzkich czopków typu krótko-, średnio- i długofalowego.

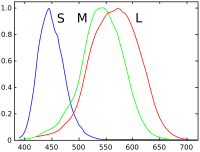
Ludzkie oko z normalnym wzrokiem ma trzy rodzaje komórek czopków , które wyczuwają światło, z pikami czułości widmowej w krótkim („S”, 420 nm – 440 nm ), środkowym („M”, 530 nm – 540 nm ) i długim („L”, 560 nm – 580 nm ) długości fal. Te czopki leżą u podstaw postrzegania kolorów przez człowieka w warunkach średniej i wysokiej jasności; w bardzo słabym świetle widzenie kolorów zmniejsza się, a monochromatyczne receptory „noktowizora” o niskiej jasności, zwane „ pręcikami ”, stają się skuteczne. Zatem trzy parametry odpowiadające poziomom bodźców trzech rodzajów czopków w zasadzie opisują każde ludzkie odczucie koloru. Ważenie całkowitego widma mocy światła przez indywidualne czułości widmowe trzech rodzajów komórek czopków daje trzy efektywne wartości bodźca ; te trzy wartości składają się na trójchromatyczną specyfikację obiektywnej barwy widma światła. Trzy parametry, oznaczone jako „S”, „M” i „L”, są wskazane przy użyciu trójwymiarowej przestrzeni określanej jako „ przestrzeń barw LMS ”, która jest jedną z wielu przestrzeni barw opracowanych do ilościowego określania widzenia barw przez człowieka .

Przestrzeń kolorów odwzorowuje zakres fizycznie wytwarzanych kolorów, od światła mieszanego, pigmentów itp., do obiektywnego opisu wrażeń kolorystycznych rejestrowanych w oku ludzkim, zwykle pod względem wartości trójchromatycznych, ale zwykle nie w przestrzeni kolorów LMS zdefiniowanej przez widmo czułość komórek czopków . Wartości trójchromatyczne związane z przestrzenią kolorów można przedstawić jako ilości trzech kolorów podstawowych w trójchromatycznym, addytywnym modelu kolorów . W niektórych przestrzeniach kolorów, w tym w przestrzeniach LMS i XYZ, używane kolory podstawowe nie są kolorami rzeczywistymi w tym sensie, że nie można ich wygenerować w żadnym widmie światła.

Przestrzeń barw CIE XYZ obejmuje wszystkie doznania kolorystyczne, które są widoczne dla osoby o przeciętnym wzroku. Dlatego CIE XYZ (wartości Tristimulus) jest reprezentacją koloru niezmienną dla urządzenia. Służy jako standardowe odniesienie, na podstawie którego definiuje się wiele innych przestrzeni kolorów. Zestaw funkcji dopasowujących kolory, takich jak krzywe czułości widmowej przestrzeni kolorów LMS , ale nie ograniczając się do nieujemnych czułości, wiąże fizycznie wytwarzane widma światła z określonymi wartościami trójchromatycznymi.

Rozważmy dwa źródła światła złożone z różnych mieszanin różnych długości fal. Takie źródła światła mogą wydawać się mieć ten sam kolor; efekt ten nazywa się „ metameryzmem ”. Takie źródła światła mają ten sam widoczny kolor dla obserwatora, gdy wytwarzają te same wartości trójbodźcowe, niezależnie od widmowego rozkładu mocy źródeł.

Większość długości fal stymuluje dwa lub wszystkie trzy rodzaje czopków, ponieważ krzywe czułości widmowej tych trzech rodzajów zachodzą na siebie. Pewne wartości trójbodźcowe są zatem fizycznie niemożliwe: np. wartości trójbodźcowe LMS, które są niezerowe dla składowej M i zerowe zarówno dla składowych L, jak i S. Co więcej, czyste kolory widmowe w dowolnej normalnej przestrzeni barw trójchromatycznych, np. przestrzeniach barw RGB , implikowałyby wartości ujemne dla co najmniej jednej z trzech barw podstawowych , ponieważ chromatyczność znajdowałaby się poza trójkątem barw określonym przez barwy podstawowe. Aby uniknąć tych ujemnych wartości RGB i mieć jeden składnik opisujący postrzeganą jasność , sformułowano „wyimaginowane” kolory podstawowe i odpowiadające im funkcje dopasowywania kolorów. Przestrzeń barw CIE 1931 definiuje wynikowe wartości trójchromatyczne, w których są one oznaczane przez „X”, „Y” i „Z”. W przestrzeni XYZ wszystkie kombinacje nieujemnych współrzędnych mają znaczenie, ale wiele z nich, na przykład główne lokalizacje [1, 0, 0], [0, 1, 0] i [0, 0, 1], odpowiada wyimaginowanym kolory poza przestrzenią możliwych współrzędnych LMS; wyimaginowane kolory nie odpowiadają żadnemu widmowemu rozkładowi długości fal i dlatego nie mają fizycznej rzeczywistości.

Znaczenie X , Y i Z

Porównanie między typową znormalizowaną czułością widmową stożka M a funkcją jasności CIE 1931 dla standardowego obserwatora w widzeniu fotopowym .

W modelu CIE 1931 Y to luminancja , Z jest prawie równe niebieskiemu (z CIE RGB), a X to mieszanka trzech krzywych CIE RGB wybranych jako nieujemne (patrz § Definicja przestrzeni kolorów CIE XYZ ) . Ustawienie Y jako luminancji ma użyteczny skutek, że dla dowolnej danej wartości Y płaszczyzna XZ będzie zawierała wszystkie możliwe chromatyczności przy tej luminancji.

Jednostka wartości trójchromatycznych X , Y i Z jest często wybierana arbitralnie, tak że Y = 1 lub Y = 100 jest najjaśniejszą bielą obsługiwaną przez kolorowy wyświetlacz. W tym przypadku wartość Y jest znana jako względna luminancja . Odpowiednie wartości punktu bieli dla X i Z można następnie wywnioskować przy użyciu standardowych źródeł światła .

Ponieważ wartości XYZ zostały określone znacznie wcześniej niż charakterystyka komórek czopków w latach pięćdziesiątych XX wieku (przez Ragnara Granita ), fizjologiczne znaczenie tych wartości jest znane dopiero znacznie później. Macierz Hunta-Pointera-Esteveza z lat 80. wiąże XYZ z LMS. Po odwróceniu pokazuje, w jaki sposób odpowiedzi trzech stożków sumują się do funkcji XYZ:

$bmatrix} X \\ Y\\Z\end{bmatrix}}=\left[{\begin{aligned}1&.910\,20\!\!\!&\!\!-1&.112\,12\!\!\! &\!\!0&.201\,91\\0&.370\,95\!\!\!&\!\!0&.629\,05\!\!\!&\!\!0&\\ 0&\!\!\!&\!\!0&\!\!\!&\!\!1&.000\,00\end{wyrównane}}\right]{\begin{bmatrix}L\\M\ \S\end{bmacierz}}_{\rm {HPE}}}$

Innymi słowy, wartość Z składa się wyłącznie z odpowiedzi stożka S, wartość Y jest mieszanką odpowiedzi L i M, a wartość X jest mieszanką wszystkich trzech. Fakt ten sprawia, że ​​wartości XYZ są analogiczne, ale różnią się od odpowiedzi czopków LMS ludzkiego oka.

Standardowy obserwator CIE

pola widzenia obserwatora . Aby wyeliminować tę zmienną, CIE zdefiniowało funkcję mapowania kolorów zwaną standardowym (kolorymetrycznym) obserwatorem , aby reprezentować reakcję chromatyczną przeciętnego człowieka w obrębie 2° łuku wewnątrz dołka . Kąt ten został wybrany ze względu na przekonanie, że czopki wrażliwe na kolor znajdowały się w obrębie 2° łuku od dołka. Tak więc CIE 1931 Standard Observer jest również znana jako CIE 1931 2° Standard Observer . Bardziej nowoczesną, ale rzadziej używaną alternatywą jest CIE 1964 10° Standard Observer , który wywodzi się z prac Stilesa i Burcha oraz Speranskaya.

W przypadku eksperymentów 10° obserwatorzy zostali poinstruowani, aby ignorować centralny punkt 2°. Funkcja dodatkowego obserwatora standardowego 1964 jest zalecana w przypadku pola widzenia większego niż około 4°. Obie standardowe funkcje obserwatora są dyskretyzowane w odstępach długości fali 5 nm od 380 nm do 780 nm i dystrybuowane przez CIE . Wszystkie odpowiednie wartości zostały obliczone na podstawie danych uzyskanych eksperymentalnie przy użyciu interpolacji . Standardowy obserwator charakteryzuje się trzema funkcjami dopasowywania kolorów .

Istnieje również zestaw danych CIE 1931 i CIE 1964 w interwale 1 nm , dostarczony przez Wyszeckiego 1982. Wydaje się, że publikacja CIE z 1986 r. również zawiera zestaw danych 1 nm, prawdopodobnie wykorzystujący te same dane. Podobnie jak zwykły zestaw danych 5 nm , ten zestaw danych również pochodzi z interpolacji.

Wyprowadzenie standardowego obserwatora CIE z eksperymentów z dopasowywaniem kolorów podano poniżej , po opisie przestrzeni CIE RGB.

Funkcje dopasowywania kolorów

Standardowe funkcje dopasowywania kolorów obserwatora CIE XYZ

Funkcje dopasowywania kolorów CIE RGB

$($ kolorów CIE _ $_$ _ $są$ numerycznym opisem odpowiedzi chromatycznej obserwatora powyżej ). Można je traktować jako krzywe czułości widmowej trzech liniowych detektorów światła, dające trójbodźcowe wartości CIE X , Y i Z. Łącznie te trzy funkcje opisują standardowego obserwatora CIE.

Przybliżenie analityczne

Wyszukiwanie w tabeli może stać się niepraktyczne w przypadku niektórych zadań obliczeniowych. Zamiast odwoływać się do opublikowanej tabeli, funkcje dopasowywania kolorów CIE XYZ można przybliżyć za pomocą sumy funkcji Gaussa w następujący sposób:

Niech g ( x ) oznacza fragmentaryczną funkcję Gaussa, zdefiniowaną przez

${\ Displaystyle g (x; \ mu, \ sigma _ {1}, \ sigma _ {2}) = {\ rozpocząć {przypadki} \ exp {\ bigl (}{- {\ tfrac {1} {2}} (x-\mu )^{2}/\sigma _{1}^{2}}{\bigr )},&x<\mu ,\\[2mu]\exp {\bigl (}{-{\tfrac {1}{2}}(x-\mu )^{2}/\sigma _{2}^{2}}{\bigr )},&x\geq \mu .\end{przypadki}}}$

Oznacza to, że g ( x ) przypomina krzywą dzwonową ze szczytem w punkcie x = μ , rozpiętością/odchyleniem standardowym σ ₁ na lewo od średniej i rozpiętością σ ₂ na prawo od średniej. Przy długości fali λ mierzonej w nanometrach przybliżamy następnie funkcje dopasowywania kolorów z 1931 roku:

${\ Displaystyle {\ rozpocząć {wyrównane} {\ overline {x}} (\ lambda) & = 1,056 g (\ lambda; 599,8,37,9,31,0) + 0,362 g (\ lambda; 442,0,16,0,26,7) \\[ 2mu]&\quad -0,065g(\lambda ;501,1,20,4,26,2),\\[5mu]{\overline {y}}(\lambda )&=0,821g(\lambda ;568,8,46,9,40,5)+ 0,286g(\lambda ;530,9,16,3,31,1),\\[5mu]{\overline {z}}(\lambda )&=1,217g(\lambda ;437,0,11,8,36,0)+0,681g(\lambda ; 459.0,26.0,13.8).\end{wyrównane}}}$

Możliwe jest również użycie mniejszej liczby funkcji gaussowskich, z jednym gaussem na każdy „płatek”. CIE 1964 dobrze pasuje do funkcji jednopłatowej.

Funkcje dopasowywania kolorów CIE XYZ są nieujemne i prowadzą do nieujemnych współrzędnych XYZ dla wszystkich rzeczywistych kolorów (to znaczy dla nieujemnych widm światła). Inni obserwatorzy, tacy jak przestrzeń CIE RGB lub inne przestrzenie kolorów RGB , są definiowani przez inne zestawy trzech funkcji dopasowywania kolorów, które nie są generalnie nieujemne, i prowadzą do wartości trójchromatycznych w tych innych przestrzeniach, które mogą obejmować współrzędne ujemne dla niektórych rzeczywistych zabarwienie.

Obliczanie XYZ z danych widmowych

Obudowa emisyjna

Wartości trójchromatyczne dla koloru o luminancji widmowej L _e,Ω,λ są podane w odniesieniu do standardowego obserwatora przez:

${\ Displaystyle {\ rozpocząć {wyrównane} X & = \ int _ {\ lambda} L _ {\ operatorname {e}, \ Omega, \ lambda} (\ lambda) \, {\ overline {x}} (\ lambda) \ ,d\lambda ,\\[6mu]Y&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {y}}(\lambda ) \,d\lambda ,\\[6mu]Z&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {z}}(\lambda )\,d\lambda .\end{wyrównane}}}$

gdzie jest długością $lambda}$ równoważnego światła monochromatycznego (mierzoną w , a całki to $λ$ displaystyle

Wartości X , Y i Z są ograniczone, jeśli widmo promieniowania Le _,Ω,λ jest ograniczone.

Futerały odblaskowe i przepuszczalne

Obudowy odblaskowe i przepuszczalne są bardzo podobne do obudowy emisyjnej, z kilkoma różnicami. Widmowa luminancja L _e,Ω,λ jest zastępowana przez widmowy współczynnik odbicia (lub transmitancję ) S(λ) mierzonego obiektu, pomnożony przez widmowy rozkład mocy źródła światła I(λ) .

${\ Displaystyle {\ rozpocząć {wyrównane} X & = {\ Frac {K} {N}} \ int _ {\ lambda} S (\ lambda) \ ,I(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[8mu]Y&={\frac {K}{N}}\int _{\lambda }S (\lambda)\,I(\lambda)\,{\overline {y}}(\lambda)\,d\lambda,\\[8mu]Z&={\frac {K}{N}}\int _ {\lambda}S(\lambda)\,I(\lambda)\,{\overline {z}}(\lambda)\,d\lambda,\end{wyrównane}}}$

Gdzie

${\ Displaystyle N = \ int _ {\ lambda} ja (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda ,}$

K to współczynnik skalowania (zwykle 1 lub 100), a $to$ światła monochromatycznego mierzona w nanometrach ), a standardowe granice całki to $lambda$ .

Diagram chromatyczności CIE xy i przestrzeń barw CIE xyY

Diagram chromatyczności przestrzeni barw CIE 1931. Zewnętrzna zakrzywiona granica to miejsce widmowe (lub monochromatyczne), z długościami fal pokazanymi w nanometrach. Zwróć uwagę, że kolory wyświetlane na ekranie na tym obrazie są określone przy użyciu sRGB , więc kolory spoza gamy sRGB nie są wyświetlane prawidłowo. W zależności od przestrzeni kolorów i kalibracji urządzenia wyświetlającego kolory sRGB również mogą nie być wyświetlane prawidłowo. Diagram ten przedstawia maksymalne nasycenie jasnych kolorów, jakie może uzyskać monitor komputera lub telewizor .

Wykres chromatyczności przestrzeni kolorów CIE 1931 przedstawiony w kategoriach kolorów o niższym nasyceniu i wartości niż przedstawione na powyższym diagramie, które mogą być wytwarzane przez pigmenty , takie jak te używane w druku . Nazwy kolorów pochodzą z systemu kolorów Munsella . Pełna krzywa z kropkami na środku, to locus Plancka , z kropkami odpowiadającymi kilku wybranym temperaturom ciała doskonale czarnego , które są wskazane tuż nad osią x.

Ponieważ ludzkie oko ma trzy rodzaje czujników kolorów, które reagują na różne zakresy długości fal , pełny wykres wszystkich widocznych kolorów jest figurą trójwymiarową. Jednak pojęcie koloru można podzielić na dwie części: jasność i chromatyczność . Na przykład kolor biały jest jasnym kolorem, podczas gdy kolor szary jest uważany za mniej jasną wersję tej samej bieli. Innymi słowy, chromatyczność bieli i szarości jest taka sama, podczas gdy ich jasność jest różna.

Przestrzeń barw CIE XYZ została celowo zaprojektowana tak, aby parametr Y był również miarą luminancji koloru . Chromatyczność jest następnie określana przez dwa pochodne parametry x i y , przy czym dwie z trzech znormalizowanych wartości są funkcjami wszystkich trzech wartości trójchromatycznych X , Y i Z :

${\ Displaystyle {\ rozpocząć {wyrównane} x & = {\ Frac {X} {X + Y+Z}}\\[5mu]y&={\frac {Y}{X+Y+Z}}\\[5mu]z&={\frac {Z}{X+Y+Z}}=1- xy \ koniec {wyrównane}}}$

Pochodna przestrzeń kolorów określona przez x , y i Y jest znana jako przestrzeń kolorów CIE xyY i jest szeroko stosowana w praktyce do określania kolorów.

Wartości trójchromatyczne X i Z można obliczyć wstecz na podstawie wartości chromatyczności x i y oraz wartości trójchromatycznej Y :

${\ Displaystyle {\ rozpocząć {wyrównane} X & = {\ Frac {Y} {y}} x, \\ [5mu] Z & = {\ Frac {Y} {y}} (1-xy). \ koniec {wyrównane }}}$

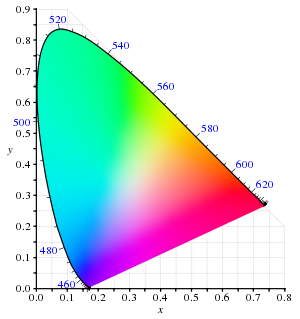
Rysunek po prawej stronie pokazuje powiązany diagram chromatyczności. Zewnętrzna zakrzywiona granica to miejsce widmowe , z długościami fal pokazanymi w nanometrach. Należy zauważyć, że wykres chromatyczności jest narzędziem do określenia, w jaki sposób ludzkie oko będzie doświadczać światła o danym widmie. Nie może określać kolorów obiektów (ani farb drukarskich), ponieważ chromatyczność obserwowana podczas patrzenia na przedmiot zależy również od źródła światła.

Z matematycznego punktu widzenia kolory diagramu chromatyczności zajmują obszar rzeczywistej płaszczyzny rzutowej .

Diagram chromatyczności ilustruje szereg interesujących właściwości przestrzeni barw CIE XYZ:

• Diagram przedstawia wszystkie chromatyczności widoczne dla przeciętnego człowieka. Są one pokazane w kolorze, a obszar ten nazywany jest gamą ludzkiego wzroku. Gama wszystkich widocznych chromatyczności na wykresie CIE to figura w kształcie języka lub podkowy pokazana w kolorze. Zakrzywiona krawędź gamy nazywana jest locus widmowym i odpowiada światłu monochromatycznemu (każdy punkt reprezentuje czysty odcień o pojedynczej długości fali), z długościami fal podanymi w nanometrach. Prosta krawędź w dolnej części gamy nazywana jest linią fioletów . Barwy te, choć znajdują się na granicy gamy, nie mają odpowiednika w świetle monochromatycznym. Mniej nasycone kolory pojawiają się we wnętrzu figury z bielą na środku.
• Widać, że wszystkie widoczne chromatyczności odpowiadają nieujemnym wartościom x , y i z (a zatem nieujemnym wartościom X , Y i Z ).
• Jeśli wybierzemy dowolne dwa punkty koloru na diagramie chromatyczności, wówczas wszystkie kolory leżące w linii prostej między tymi dwoma punktami można utworzyć przez zmieszanie tych dwóch kolorów. Wynika z tego, że gama kolorów musi mieć kształt wypukły . Wszystkie kolory, które można utworzyć przez zmieszanie trzech źródeł, znajdują się wewnątrz trójkąta utworzonego przez punkty źródłowe na diagramie chromatyczności (i tak dalej dla wielu źródeł).
• Równa mieszanina dwóch jednakowo jasnych kolorów na ogół nie będzie leżeć na środku tego odcinka linii . Mówiąc bardziej ogólnie, odległość na wykresie chromatyczności CIE xy nie odpowiada stopniowi różnicy między dwoma kolorami. We wczesnych latach czterdziestych David MacAdam badał naturę wrażliwości wzrokowej na różnice kolorów i podsumował swoje wyniki w koncepcji elipsy MacAdama . Na podstawie prac MacAdama opracowano przestrzenie kolorów CIE 1960 , CIE 1964 i CIE 1976 , których celem było osiągnięcie percepcyjnej jednolitości (jednakowa odległość w przestrzeni kolorów odpowiada równym różnicom w kolorze). Chociaż były one wyraźnym ulepszeniem w stosunku do systemu CIE 1931, nie były całkowicie wolne od zniekształceń.
• Można zauważyć, że biorąc pod uwagę trzy rzeczywiste źródła, źródła te nie mogą obejmować gamy ludzkiego wzroku. Mówiąc geometrycznie, w gamie nie ma trzech punktów, które tworzą trójkąt obejmujący całą gamę; lub prościej, gama ludzkiego wzroku nie jest trójkątem.
• Światło o płaskim widmie mocy pod względem długości fali (jednakowa moc w każdym przedziale 1 nm ) odpowiada punktowi ( x , y ) = (1/3, 1/3) .

Mieszanie kolorów określone za pomocą diagramu chromatyczności CIE xy

Kiedy dwa lub więcej kolorów jest mieszanych addytywnie, współrzędne chromatyczności x i y otrzymanego koloru (x _mix ,y _mix ) można obliczyć z chromatyczności składników mieszaniny (x ₁ , y ₁ ; x ₂ , y ₂ ; … ; x _n , y _n ) i odpowiadające im luminancje (L ₁ , L ₂ , …, L _n ) o następujących wzorach:

${\ Displaystyle x _ {\ operatorname {mix}} = {\ Frac {{\ dfrac {x_ {1}} {y_{1}}}L_{1}+{\dfrac {x_{2}}{y_{2}}}L_{2}+\kropki +{\dfrac {x_{n}}{y_{n} }}L_{n}}{{\dfrac {L_{1}}{y_{1}}}+{\dfrac {L_{2}}{y_{2}}}+\dots +{\dfrac {L_ {n}}{y_{n}}}}}\quad ,\quad y_{\mathrm {mix}}={\frac {L_{1}+L_{2}+\kropki +L_{n}}{ {\dfrac {L_{1}}{y_{1}}}+{\dfrac {L_{2}}{y_{2}}}+\kropki +{\dfrac {L_{n}}{y_{n }}}}}}$

Wzory te można wyprowadzić z przedstawionych wcześniej definicji współrzędnych chromatyczności x i y, wykorzystując fakt, że wartości trójchromatyczne X, Y i Z poszczególnych składników mieszaniny są wprost addytywne. Zamiast wartości luminancji (L ₁ , L ₂ , itd.) można alternatywnie użyć dowolnej innej wielkości fotometrycznej, która jest wprost proporcjonalna do wartości trójchromatycznej Y (co oczywiście oznacza, że ​​samo Y również może być użyte).

Jak już wspomniano, po zmieszaniu dwóch kolorów wynikowy kolor x _mix , y _mix będzie leżeć na odcinku linii prostej, który łączy te kolory na diagramie chromatyczności CIE xy. Aby obliczyć stosunek mieszania składowych kolorów x ₁ ,y ₁ i x ₂ ,y ₂ , który daje określony x _mix ,y _mix na tym odcinku linii, można skorzystać ze wzoru

${\ Displaystyle {\ Frac {L_ {1}} {L_ {2}}} = {\ Frac {y_ {1} \ lewo (x_ {2} -x_ {\ operatorname {mix}} \ prawej)} {y_ {2}\left(x_{\mathrm {mix}}-x_{1}\right)}}={\frac {y_{1}\left(y_{2}-y_{\mathrm {mix} }\ prawo)}{y_{2}\left(y_{\mathrm {mix}}-y_{1}\right)}}}$

gdzie L ₁ to luminancja koloru x ₁ ,y ₁ a L ₂ to luminancja koloru x ₂ ,y ₂ . Zauważ, że ponieważ y _mix jest jednoznacznie określony przez x _mix i vice versa, znajomość tylko jednego lub drugiego z nich wystarczy do obliczenia proporcji mieszania. Należy również zauważyć, że zgodnie z uwagami dotyczącymi wzorów na xmix _i ymix _, stosunek mieszania L1 _/ L2 _można równie dobrze wyrazić za pomocą innych wielkości fotometrycznych niż luminancja.

Definicja przestrzeni barw CIE XYZ

Przestrzeń barw CIE RGB

Gama prawyborów CIE RGB i lokalizacja prawyborów na diagramie chromatyczności xy CIE 1931 .

Funkcje dopasowywania kolorów CIE 1931 RGB. Funkcje dopasowywania kolorów to ilości kolorów podstawowych potrzebnych do dopasowania monochromatycznego koloru testowego przy długości fali pokazanej na skali poziomej.

Kostka kolorów CIE RGB (obraz zakodowany profilem ICC)

Przestrzeń kolorów CIE RGB jest jedną z wielu przestrzeni kolorów RGB , wyróżniających się określonym zestawem monochromatycznych (o jednej długości fali) kolorów podstawowych .

W latach dwudziestych XX wieku W. David Wright z dziesięcioma obserwatorami i John Guild z siedmioma obserwatorami przeprowadzili dwa niezależne eksperymenty dotyczące postrzegania kolorów przez ludzi. Ich wyniki położyły podwaliny pod specyfikację trójchromatycznej przestrzeni barw CIE XYZ.

Eksperymenty przeprowadzono przy użyciu okrągłego podzielonego ekranu (dwuczęściowego pola) o średnicy 2 stopni, co odpowiada rozmiarowi kątowemu dołka ludzkiego . Po jednej stronie testowy , a po drugiej kolor regulowany przez obserwatora. Regulowany kolor był mieszanką trzech podstawowych kolorów, każdy o stałej chromatyczności , ale z regulowaną jasnością .

Obserwator zmieniał jasność każdej z trzech głównych wiązek, aż do zaobserwowania dopasowania do koloru testowego. Ponieważ gama RGB nie obejmuje całego spektrum kolorów, nie wszystkie kolory testowe można było dopasować przy użyciu tej techniki. W takim przypadku do koloru testowego można było dodać zmienną ilość jednego z kolorów podstawowych i przeprowadzono dopasowanie z pozostałymi dwoma kolorami podstawowymi ze zmienną plamą koloru. W tych przypadkach ilość barwnika podstawowego dodanego do koloru testowego uznano za wartość ujemną. W ten sposób można by objąć cały zakres ludzkiej percepcji kolorów. Gdy kolory testowe były monochromatyczne, można było sporządzić wykres ilości każdego zastosowanego koloru podstawowego w funkcji długości fali koloru testowego. Te trzy funkcje są nazywane funkcjami dopasowywania kolorów dla tego konkretnego eksperymentu.

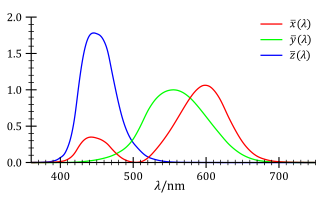
Chociaż eksperymenty Wrighta i Guilda przeprowadzono przy użyciu różnych prawyborów przy różnych intensywnościach i chociaż korzystali z wielu różnych obserwatorów, wszystkie ich wyniki zostały podsumowane za pomocą znormalizowanych funkcji dopasowywania kolorów CIE RGB r ¯ ( λ ) $overline {r}} (\ lambda)}$ sol ${\ Displaystyle {\ overline {g}} (\ lambda)}$ i $}} (\ lambda )}$ , otrzymane przy użyciu trzech monochromatycznych kolorów podstawowych przy znormalizowanych długościach fali 700 nm (czerwony), 546,1 nm (zielony) i 435,8 nm (niebieski). Funkcje dopasowywania kolorów to ilości kolorów podstawowych potrzebnych do dopasowania podstawowego testu monochromatycznego. Funkcje te są pokazane na wykresie po prawej stronie (CIE 1931). Zauważ, że $overline {g}} (\ lambda)}$ Ż $Displaystyle {$ \ przy 435,8 nm ${\ Displaystyle {\ overline {r}} (\ lambda)}$ i ${\ Displaystyle {\ overline {b}} (\ lambda)}$ wynoszą zero przy 546,1 nm i ${\ Displaystyle {\ overline {g}} (\ lambda)}$ i ${\ Displaystyle {\ overline {b}} (\ lambda)}$ wynoszą zero przy 700 nm , ponieważ w tych przypadkach kolor testowy jest jednym z pierwszorzędnych. Wybrano prążki o długościach fali 546,1 nm i 435,8 nm , ponieważ są to łatwo powtarzalne monochromatyczne linie wyładowania par rtęci. Wybrano długość 700 nm , którą w 1931 roku trudno było odtworzyć jako wiązkę monochromatyczną, ponieważ postrzeganie koloru przez oko jest raczej niezmienne przy tej długości fali, a zatem małe błędy w długości fali tej podstawowej miałyby niewielki wpływ na wyniki.

Funkcje dopasowywania kolorów i prawybory zostały ustalone przez specjalną komisję CIE po długich obradach. Odcięcia po stronie krótkiej i długiej fali diagramu są wybierane nieco arbitralnie; oko ludzkie faktycznie widzi światło o długości fali do około 810 nm , ale z czułością, która jest wiele tysięcy razy mniejsza niż w przypadku światła zielonego. Te funkcje dopasowywania kolorów definiują to, co jest znane jako „standardowy obserwator CIE z 1931 r.”. Należy zauważyć, że zamiast określać jasność każdego elementu podstawowego, krzywe są znormalizowane, aby miały pod nimi stałą powierzchnię. Ten obszar jest ustalany na określoną wartość poprzez jej określenie

${\ Displaystyle \ int _ {0} ^ {\ infty} {\ overline {r}} (\ lambda) \, d \ lambda = \ int _ {0} ^ {\ infty} {\ overline {g}} ( \lambda )\,d\lambda =\int _{0}^{\infty}{\overline {b}}(\lambda)\,d\lambda.}$

Otrzymane znormalizowane funkcje dopasowywania kolorów są następnie skalowane w stosunku r:g:b wynoszącym 1:4,5907:0,0601 dla luminancji źródła i 72,0962:1,3791:1 dla jasności źródła , aby odtworzyć rzeczywiste funkcje dopasowywania kolorów. Proponując standaryzację prawyborów, CIE ustanowiła międzynarodowy system obiektywnej notacji kolorów.

trójchromatyczne RGB dla koloru z widmowym rozkładem mocy byłyby wtedy określone przez: ${\ Displaystyle S (\ lambda)}$

${\ Displaystyle {\ rozpocząć {wyrównane} R & = \ int _ {0} ^ {\ infty} S (\ lambda) \ {\ overline {r}} (\ lambda) \, d \ lambda, \\ [6 mu ]G&=\int _{0}^{\infty}S(\lambda )\,{\overline {g}}(\lambda)\,d\lambda ,\\[6mu]B&=\int _{0 }^{\infty}S(\lambda )\,{\overline {b}}(\lambda)\,d\lambda .\end{wyrównane}}}$

Są to wszystkie produkty wewnętrzne i można je traktować jako projekcję nieskończenie wymiarowego widma na trójwymiarowy kolor .

prawa Grassmanna

Główny artykuł: prawa Grassmanna (nauka o kolorze)

Ktoś mógłby zapytać: „Dlaczego jest możliwe, że wyniki Wrighta i Guilda można podsumować przy użyciu innych prawyborów i różnych intensywności niż te, które faktycznie zastosowano?” Można też zapytać: „A co w przypadku, gdy dopasowywane kolory testowe nie są monochromatyczne?” Odpowiedź na oba te pytania leży w (prawie) liniowości postrzegania kolorów przez człowieka. Ta liniowość jest wyrażona w prawach koloru Grassmanna.

Przestrzeń CIE RGB może być użyta do zdefiniowania chromatyczności w zwykły sposób: Współrzędne chromatyczności to r , g i b gdzie:

${\ Displaystyle {\ rozpocząć {wyrównane} r & = {\ Frac {R} {R + G + B}}, \\ [5mu] g & = {\ Frac {G} {R + G + B}}, \\ [5mu]b&={\frac {B}{R+G+B}}.\end{wyrównane}}}$

Konstrukcja przestrzeni barw CIE XYZ na podstawie danych Wright-Guild

Gama sRGB ( po lewej ) i widzialna przy oświetleniu D65 ( po prawej ) wyświetlana w przestrzeni kolorów CIEXYZ. X i Z to osie poziome; Y to oś pionowa.

Gama sRGB ( po lewej ) i widzialna przy oświetleniu D65 ( po prawej ) wyświetlana w przestrzeni kolorów CIExyY. x i y to osie poziome; Y to oś pionowa.

Po opracowaniu modelu RGB ludzkiego wzroku z wykorzystaniem funkcji dopasowujących CIE RGB, członkowie specjalnej komisji chcieli opracować inną przestrzeń barw, która odnosiłaby się do przestrzeni barw CIE RGB. Założono, że obowiązuje prawo Grassmanna, a nowa przestrzeń będzie powiązana z przestrzenią CIE RGB przez przekształcenie liniowe. Nowa przestrzeń byłaby zdefiniowana za pomocą trzech nowych funkcji dopasowywania kolorów ${\ Displaystyle {\ overline {x}} (\ lambda)}$ , ${\ Displaystyle {\ overline {y}} (\ lambda)}$ i jak opisano powyżej. ${\ Displaystyle {\ overline {z}} (\ lambda)}$ Nowa przestrzeń kolorów zostałaby wybrana tak, aby miała następujące pożądane właściwości:

Diagram w przestrzeni chromatyczności CIE rg przedstawiający budowę trójkąta określającego przestrzeń barw CIE XYZ. Trójkąt Cb _- Cg _- Cr _jest po prostu trójkątem xy = (0, 0), (0, 1), (1, 0) w przestrzeni chromatyczności CIE xy . Linia łącząca C _b i Cr _to alychne. Zauważ, że miejsce widmowe przechodzi przez rg = (0, 0) przy 435,8 nm , przez rg = (0, 1) przy 546,1 nm i przez rg = (1, 0) przy 700 nm . Również punkt równej energii (E) znajduje się w rg = xy = (1/3, 1/3) .

1. Nowe funkcje dopasowywania kolorów miały być wszędzie większe lub równe zeru. W 1931 r. obliczenia wykonywano ręcznie lub suwakiem logarytmicznym, a podanie wartości dodatnich było użytecznym uproszczeniem obliczeniowym.
2. Funkcja $dopasowywania$ kolorów byłaby dokładnie równa świetlnej V λ ) dla „standardowego obserwatora fotopowego CIE” Funkcja luminancji opisuje zmianę postrzeganej jasności wraz z długością fali. Fakt, że funkcja luminancji może być skonstruowana przez liniową kombinację funkcji dopasowywania kolorów RGB, nie był w żaden sposób gwarantowany, ale można się spodziewać, że będzie prawie prawdziwy ze względu na prawie liniowy charakter ludzkiego wzroku. Ponownie, głównym powodem tego wymogu było uproszczenie obliczeń.
3. Dla punktu bieli o stałej energii wymagane było, aby x = y = z = 1/3 .
4. Na mocy definicji chromatyczności i wymogu dodatnich wartości x i y można zauważyć, że gama wszystkich kolorów będzie leżeć wewnątrz trójkąta [1, 0], [0, 0], [0, 1] . Wymagane było, aby gama wypełniła tę przestrzeń praktycznie całkowicie.
5. Stwierdzono, że $funkcja$ dopasowywania kolorów może być ustawiona na zero powyżej nm w granicach błędu Dla uproszczenia obliczeń określono, że tak będzie.

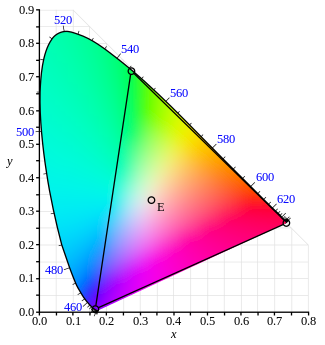
Pod względem geometrycznym wybór nowej przestrzeni kolorów jest równoznaczny z wyborem nowego trójkąta w przestrzeni chromatyczności rg . Na rysunku powyżej po prawej rg są pokazane na dwóch osiach w kolorze czarnym, wraz z gamą standardowego obserwatora z 1931 roku. Na czerwono pokazane są osie chromatyczności CIE xy , które zostały określone na podstawie powyższych wymagań. Wymóg, aby współrzędne XYZ były nieujemne, oznacza, że ​​trójkąt utworzony przez C _r , C _g , C _b musi obejmować całą gamę standardowego obserwatora. Linia łącząca C $funkcja$ _i C _b przez wymaganie, aby była równa funkcji Ta linia jest linią zerowej luminancji i nazywa się alychne. Wymóg, aby _wynosiła zero powyżej 650 nm oznacza $, że$ C _g C musi być styczna do gamy w Kr . _{_} To definiuje położenie punktu C _r . Wymóg, aby punkt równej energii był określony przez x = y = 1/3 nakłada ograniczenie na linię łączącą C _b i C _g , a wreszcie wymóg, aby gama wypełniała przestrzeń nakłada drugie ograniczenie na tę linię bardzo blisko gamy w obszarze zielonym, który określa położenie C _g i C _b . Opisana powyżej transformacja jest transformacją liniową z przestrzeni CIE RGB do przestrzeni XYZ. Standardowa transformacja ustalona przez specjalną komisję CIE wyglądała następująco:

Liczby w poniższej macierzy konwersji są dokładne, z liczbą cyfr określoną w standardach CIE.

${\ Displaystyle {\ rozpocząć {wyrównane} {\ rozpocząć {bmatrix} X \\ Y \\ Z \ koniec {bmatrix}} i = {\ rozpocząć {bmatrix} b_ {11} & b_ {$

Powyższa macierz jest zrównoważona dla bodźca równoenergetycznego: ma współrzędne (1,1,1) zarówno we współrzędnych RGB, jak i XYZ.

Chociaż powyższa macierz jest dokładnie określona w standardach, odwrotność pozostaje nieokreślona, ​​aby można ją było przybliżyć do precyzji maszyny, aby zmniejszyć błędy zaokrąglania w obie strony. Jego wartości można dokładnie obliczyć za pomocą liczb wymiernych:

${\ Displaystyle {\ rozpocząć {bmatrix} R \ \ G \\ B \ koniec {b macierz}$

Który ma te przybliżone wartości:

${\ Displaystyle {\ rozpocząć {bmatrix} R \\ G \\ B\end{bmatrix}}\około {\begin{bmatrix}2,364\,61385&-0,896\,54057&-0,468\,07328\\-0,515\,16621&1,426\,4081&0,088\,7581\\0,005\ ,2037&-0.014\,40816&1.009\,20446\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$

Całki funkcji dopasowywania kolorów XYZ muszą być równe zgodnie z wymaganiem 3 powyżej, a jest to określone przez całkę funkcji fotopowej wydajności świetlnej zgodnie z wymaganiem 2 powyżej. Zestawione w tabeli krzywe wrażliwości mają w sobie pewną dozę arbitralności. Kształty poszczególnych X , Y i Z można zmierzyć z rozsądną dokładnością. Jednak ogólna krzywa jasności (która w rzeczywistości jest ważoną sumą tych trzech krzywych) jest subiektywna, ponieważ polega na zapytaniu osoby testującej, czy dwa źródła światła mają taką samą jasność, nawet jeśli mają zupełnie różne kolory. Wzdłuż tych samych linii względne wielkości krzywych X , Y i Z są dowolne. Ponadto można zdefiniować prawidłową przestrzeń kolorów za pomocą X , która ma dwukrotnie większą amplitudę. Ta nowa przestrzeń kolorów miałaby inny kształt. Krzywe czułości w przestrzeniach kolorów CIE 1931 i 1964 XYZ są skalowane tak, aby miały równe pola pod krzywymi.

Podobne przestrzenie barw

Dostępnych jest kilka innych funkcji dopasowywania kolorów w stylu XYZ. Funkcje te implikują własne przestrzenie kolorów podobne do XYZ i xyY.

Korekty Judda i Vosa dla 2° CMF

Wiadomo, że CIE 1931 CMF nie docenia wkładu krótszych fal niebieskich. Judd (1951) i jego późniejsze poprawki Vos (1978) miały na celu naprawienie problemu bez odchodzenia od oryginalnej metodologii.

CIE 1964 X ₁₀ Y ₁₀ Z ₁₀

X ₁₀ Y ₁₀ Z ₁₀ (również zapisywany jako XYZ ₁₀ i analogicznie dla poniższych) to przestrzeń kolorów w stylu XYZ zdefiniowana przy użyciu CMF obserwatora CIE 1964 10°.

CIE 170-2 X _F Y _F Z _F

X _F Y _F Z _F to przestrzeń kolorów w stylu XYZ zdefiniowana za pomocą fizjologicznego obserwatora 2° Stockmana i Sharpe'a (2000), który z kolei jest liniową kombinacją podstaw LMS grupy . Dane CMF wraz z fizjologicznym zestawem danych 10° są dostępne w laboratorium Color & Vision Research na University College London do rozdzielczości 0,1 nm.

CIE 170-2 X _F,10 Y _F,10 Z _F,10

Ta przestrzeń jest oparta na fizjologicznym obserwatorze 10° Stockmana i Sharpe'a (2000).

Według firmy Konica Minolta starszy model CIE 1931 CMF wykazuje awarię metameryzmu (brak możliwości przewidzenia, kiedy kolory wydają się takie same) dla wyświetlaczy o szerokiej gamie kolorów zawierających emitery wąskopasmowe, takie jak OLED , podczas gdy XYZ _F CMF z 2015 r. nie jest narażony. Starsze Sony zalecają stosowanie korekcji Judd-Vos poprzez zastosowanie przesunięcia punktu bieli w zależności od zastosowanej technologii wyświetlania.

Zobacz też

• trichromacja
• Niemożliwy kolor
• Przestrzeń barw CIELAB
• Standardowe źródło światła , definicja punktu bieli stosowana przez CIE i powszechnie pokazywana na diagramach przestrzeni kolorów jako E, D50 lub D65

Dalsza lektura

• Broadbent, Arthur D. (sierpień 2004). „Krytyczny przegląd rozwoju funkcji dopasowywania kolorów CIE1931 RGB” . Badania i zastosowanie kolorów . 29 (4): 267–272. doi : 10.1002/col.20020 . W tym artykule opisano rozwój współrzędnych chromatyczności CIE1931 i funkcji dopasowywania kolorów, począwszy od początkowych danych eksperymentalnych WD Wrighta i J. Guilda. Podano wystarczającą ilość informacji, aby czytelnik mógł odtworzyć i zweryfikować wyniki otrzymane na każdym etapie obliczeń oraz krytycznie przeanalizować zastosowane procedury. Niestety, niektóre informacje wymagane do przekształceń współrzędnych nigdy nie zostały opublikowane, a załączone tabele zawierają prawdopodobne wersje tych brakujących danych.
• Trezona, Pat W. (2001). „Wyprowadzenie funkcji dopasowywania kolorów CIE 10 ° XYZ z 1964 r. I ich zastosowanie w fotometrii”. Badania i zastosowanie kolorów . 26 (1): 67–75. doi : 10.1002/1520-6378(200102)26:1<67::AID-COL7>3.0.CO;2-4 .
•   Wright, William David (2007). „Złoty jubileusz koloru w CIE - historyczne i eksperymentalne tło systemu kolorymetrii CIE z 1931 r.”. W Schanda, János (red.). Kolorymetria . Wiley Interscience. s. 9–24. doi : 10.1002/9780470175637.ch2 . ISBN 978-0-470-04904-4 . (pierwotnie opublikowane przez Society of Dyers and Colourists , Bradford, 1981.)

Linki zewnętrzne

• Wprowadzenie do nauki o kolorze , William Andrew Steer.
• Raport laboratoryjny firmy efg dotyczący diagramów chromatyczności kolorów i źródło Delphi
• Przestrzeń barw CIE , Gernot Hoffmann
• Tabele danych do pobrania z adnotacjami , Andrew Stockman i Lindsay T. Sharpe.
• Obliczenia na podstawie oryginalnych danych eksperymentalnych współrzędnych chromatyczności widmowej obserwatora standardowego CIE 1931 RGB i funkcji dopasowywania kolorów
• Dane kolorymetryczne przydatne do obliczeń , w różnych formatach plików
• Colorlab MATLAB do obliczeń z zakresu nauki o kolorach i dokładnego odtwarzania kolorów (autorzy: Jesus Malo i Maria Jose Luque, Universitat de Valencia). Obejmuje standardową kolorymetrię trójchromatyczną CIE i transformacje do wielu nieliniowych modeli wyglądu kolorów (CIE Lab, CIE CAM itp.).
• Precyzyjna komunikacja kolorów Spojrzenie na przeszłość i przyszłość binningu LED
• [1] Pomiar koloru w świecie światła