Częstotliwość Matsubary

W termicznej kwantowej teorii pola sumowanie częstotliwości Matsubary ( nazwane na cześć Takeo Matsubary ) jest sumowaniem po dyskretnych urojonych częstotliwościach. Przyjmuje następującą formę

${\ Displaystyle S _ {\ eta} = {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {n}} g ( i\omega _{n}),}$

gdzie ${\ Displaystyle \ beta = \ hbar / k _ {\ rm {B}} T}$ jest temperaturą odwrotną, a częstotliwości są zwykle pobierane z ${\ Displaystyle \ omega _ {n}}$ jeden z następujących dwóch zestawów (z ${\ displaystyle n \ in \ mathbb {Z}}$ ):

częstotliwości bozonowe: ${\ Displaystyle \ omega _ {n} = {\ Frac {2n \ pi} {\ beta}},}$

częstotliwości fermionowe: $\ Displaystyle \ omega _ {n} = {\ Frac {(2n + 1) \ pi} {\ beta}},}$

Sumowanie będzie zbieżne, jeśli $niż$$\displaystyle z^{-1}}$ do 0 w granicy $\ do \ infty$${ \ Displaystyle$ w . Sumowanie po częstotliwościach bozonowych jest oznaczone jako $η$ = $Displaystyle \ eta = + 1}$ ), podczas gdy powyżej częstotliwości fermionowych jest oznaczane jako $)$ z $-1}$ . ${\ displaystyle \ eta}$ jest znakiem statystycznym.

Oprócz termicznej kwantowej teorii pola, metoda sumowania częstotliwości Matsubary odgrywa również istotną rolę w schematycznym podejściu do fizyki ciała stałego, a mianowicie, jeśli weźmie się pod uwagę diagramy w skończonej temperaturze.

Ogólnie rzecz biorąc, jeśli w $,$ pewien diagram Feynmana $\ int _ { T = 0} \ operatorname {d} \ omega \ g (\ omega)}$ przez całkę , w skończonej temperaturze jest to suma ${\ Displaystyle S _ {\ eta}}$ .

Formalizm sumacyjny

Formalizm ogólny

Rysunek 1.

Rysunek 2.

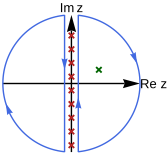
$miejscu$ funkcji ważenia Matsubary h _η ( z ), która ma proste zlokalizowane w . Funkcje ważenia w przypadku bozonu η = +1 i fermionu η = −1 różnią się. Wybór funkcji ważenia zostanie omówiony później. Dzięki funkcji ważenia sumowanie można zastąpić całką po konturze otaczającą urojoną oś.

${\ Displaystyle S _ {\ eta} = {\ Frac {1} {\ beta }}\sum _{i\omega }g(i\omega )={\frac {1}{2\pi i\beta }}\oint g(z)h_{\eta }(z)\,dz, }$

Podobnie jak na ryc. 1, funkcja ważenia generuje bieguny (czerwone krzyżyki) na urojonej osi. Całka konturowa pobiera resztę tych biegunów, co jest równoważne z sumowaniem.

Poprzez odkształcenie linii konturowych w celu objęcia biegunów g ( z ) (zielony krzyżyk na ryc. 2), sumowanie można formalnie przeprowadzić, sumując resztę g ( z ) h _η ( z ) na wszystkich biegunach g ( z ),

${\ Displaystyle S _ {\ eta} = - {\ Frac {1} {\ beta}} \ suma _ {z_ {0} \ w g (z) {\ tekst {bieguny}}} \ operatorname {Res} g ( z_{0})h_{\eta}(z_{0}).}$

Należy zauważyć, że znak minus jest tworzony, ponieważ kontur jest zdeformowany, aby objąć bieguny w kierunku zgodnym z ruchem wskazówek zegara, co skutkuje pozostałością ujemną.

Wybór funkcji ważenia Matsubara

Aby wytworzyć proste bieguny na częstotliwościach bozonu $można$ wybrać jeden z dwóch poniższych typów

${\ Displaystyle h _ {\ rm {B}} ^ { (1)}(z)={\frac {\beta }{1-e^{-\beta z}}}=-\beta n_{\rm {B}}(-z)=\beta (1+ n_{\rm {B}}(z)),}$

${\ Displaystyle h _ {\ rm {B}} ^ {(2)} (z) = {\ Frac {- \ beta} {1- e^{\beta z}}}=\beta n_{\rm {B}}(z),}$

${\ Displaystyle h _ {\ rm {B}} ^ {(1)} (z)}$ kontroluje zbieżność w lewej półpłaszczyźnie (Re z <0), podczas gdy ${\ Displaystyle h _ {\ rm {B}} ^ {(2)} (z)}$ kontroluje zbieżność w prawej półpłaszczyźnie (Re z > 0 ). Tutaj ${\ Displaystyle n _ {\ rm {B}} (z) = (e ^ {\ beta z} -1) ^ {- 1}} jest dystrybuantą$ Bosego - Einsteina .

Podobnie jest w przypadku częstotliwości fermionowych. Istnieją również dwa rodzaje funkcji ważenia Matsubara, które tworzą proste bieguny w ${\ Displaystyle z = i \ omega _ {m}}$

${\ Displaystyle h _ {\ rm {F}} ^ {( 1)}(z)={\frac {\beta}{1+e^{-\beta z}}}=\beta n_{\rm {F}}(-z)=\beta (1-n_{ \rm {F}}(z)),}$

${\ Displaystyle h _ {\ rm {F}} ^ {(2)} (z) = {\ Frac {- \ beta} {1 + e ^ {\ beta z}}} = - \ beta n_ {\ rm { F z).}$

${\ Displaystyle h _ {\ rm {F}} ^ {(1)} (z)}$ kontroluje zbieżność w lewej półpłaszczyźnie (Re z <0), podczas gdy ${\ Displaystyle h _ {\ rm {F}} ^ {(2)} (z)}$ kontroluje zbieżność w prawej półpłaszczyźnie (Re z > 0). Tutaj $.$ dystrybuantą Fermiego – Diraca

W zastosowaniu do obliczania funkcji Greena g ( z ) zawsze mają strukturę

${\ Displaystyle g (z) = G (z) e ^ {- z \ tau},}$

która rozchodzi się w lewej półpłaszczyźnie, biorąc pod uwagę 0 < τ < β . Aby $_ (1)}(z)}$ . Jednak nie ma potrzeby kontrolowania zbieżności, jeśli sumowanie Matsubary nie jest rozbieżne, w takim przypadku dowolny wybór funkcji ważenia Matsubary doprowadzi do identycznych wyników.

Tabela podsumowań częstotliwości Matsubary

Poniższa tabela zawiera ${\ Displaystyle S _ {\ eta} = {\ Frac {1} {\ beta}} \ suma _ {i \ omega} g (i \ omega )}$ dla niektórych prostych funkcji wymiernych g ( z ). Symbol η = ±1 jest znakiem statystycznym.

${\ Displaystyle g (i \ omega)}$	${\ Displaystyle S _ {\ eta}}$
${\ Displaystyle (i \ omega - \ xi) ^ {- 1}}$	${\ Displaystyle - \ eta n_ {\ eta} (\ xi)}$ [1]
${\ Displaystyle (i \ omega - \ xi) ^ {- 2}}$	${\ Displaystyle - \ eta n_ {\ eta} ^ {\ pierwsza} (\ xi) = \ beta n_ {\ eta }(\xi )(\eta +n_{\eta }(\xi ))}$
${\ Displaystyle (i \ omega - \ xi) ^ {- n}}$	${\ Displaystyle - {\ Frac {\ eta} {(n-1)!}} \ częściowe _ {\ xi} ^ {n-1} n_ {\ eta} (\ xi)}$
${\ Displaystyle {\ Frac {1} {(i \ omega - \ xi _ {1}) (i \ omega - \ xi _ {2})} }}$	${\ Displaystyle - {\ Frac {\ eta (n_ {\ eta} (\ xi _ {1}) -n_ {\ eta }(\xi _{2})}}{\xi _{1}-\xi _{2}}}}$
${\ Displaystyle {\ Frac {1} {(i \ omega - \ xi _ {1}) ^ {2} (i \ omega - \ xi _{2})^{2}}}}$	${\ Displaystyle {\ Frac {\ eta} {(\ xi _ {1} - \ xi _ {2}) ^ {2}}} \ lewo ({\ Frac {2 (n_ {\ eta} (\ xi _ {1})-n_{\eta }(\xi _{2})}}{\xi _{1}-\xi _{2}}}-(n_{\eta}^{\prime}(\ xi _{1})+n_{\eta}^{\prime}(\xi _{2}))\right)}$
${\ Displaystyle {\ Frac {1} {(i \ omega - \ xi _ {1}) ^ {2} - \ xi _ {2} ^ {2} }}}$	${\ Displaystyle \ eta c_ {\ eta} (\ xi _ {1}, \ xi _ {2})}$
${\ Displaystyle {\ Frac {1} {(i \ omega) ^ {2} - \ xi ^ {2}}}}$	${\ Displaystyle \ eta c_ {\ eta} (0, \ xi) = - {\ Frac {1} {2 \ xi }}(1+2\eta n_{\eta }(\xi ))}$
${\ Displaystyle {\ Frac {(i \ omega) ^ {2}} {(i \ omega) ^ {2} - \ xi ^ {2}}}}$	${\ Displaystyle - {\ Frac {\ xi} {2}} (1 + 2 \ eta n_ {\ eta} (\ xi))} [1$ ]
${\ Displaystyle {\ Frac {1} {((i \ omega) ^ {2} - \ xi ^ {2}) ^ {2}}}}$	${\ Displaystyle - {\ Frac {\ eta} {2 \ xi ^ {2}}} (c_ {\ eta} (0, \xi )+n_{\eta }^{\prime }(\xi ))}$
${\ Displaystyle {\ Frac {(i \ omega) ^ {2}} {((i \ omega) ^ {2} - \ xi ^ {2 })^{2}}}}$	${\ Displaystyle {\ Frac {\ eta} {2}} (c_ {\ eta} (0, \ xi) -n_ {\ eta} ^ {\pierwsza}(\xi)}}$
${\ Displaystyle {\ Frac {(i \ omega) ^ {2} + \ xi ^ {2}} {((i \ omega) ^{2}-\xi ^{2})^{2}}}}$	${\ Displaystyle - \ eta n_ {\ eta} ^ {\ pierwsza} (\ xi) = \ beta n_ {\ eta }(\xi )(\eta +n_{\eta }(\xi ))}$
${\ Displaystyle {\ Frac {1} {((i \ omega) ^ {2} - \ xi _ {1} ^{2})((i\omega)^{2}-\xi_{2}^{2})}}}$	${\ Displaystyle {\ Frac {\ eta (c_ {\ eta} (0, \ xi _ {1}) -c_{\eta }(0,\xi_{2})}}{\xi_{1}^{2}-\xi_{2}^{2}}}}$
${\ Displaystyle \ lewo ({\ Frac {1} {(i \ omega) ^ {2} - \ xi _ {1}^{2}}}+{\frac {1}{(i\omega)^{2}-\xi _{2}^{2}}}\right)^{2}}$	${\ Displaystyle \ eta \ lewo ({\ Frac {3 \ xi _ {1} ^ {2} + \ xi _ {2} ^ {2}} {2 \ xi _ {1} ^ {2} (\ xi _{1}^{2}-\xi _{2}^{2})}}c_{\eta }(0,\xi _{1})-{\frac {n_{\eta}^{\ liczba pierwsza }(\xi _{1})}{2\xi _{1}^{2}}}\right)+(1\leftrightarrow 2)}$ [2]
${\ Displaystyle \ lewo ({\ Frac {1} {(i \ omega) ^ {2} - \ xi _ {1}^{2}}}-{\frac {1}{(i\omega)^{2}-\xi _{2}^{2}}}\right)^{2}}$	${\ Displaystyle \ eta \ lewo (- {\ Frac {5 \ xi _ {1} ^ {2} - \ xi _ {2} ^ {2}} {2 \ xi _ {1} ^ {2} (\ xi _{1}^{2}-\xi _{2}^{2})}}c_{\eta }(0,\xi _{1})-{\frac {n_{\eta}^{ \prime }(\xi _{1})}{2\xi _{1}^{2}}}\right)+(1\leftrightarrow 2)}$ [2]

[1] Ponieważ sumowanie nie jest zbieżne, wynik może się różnić w zależności od innego wyboru funkcji ważenia Matsubary.

[2] (1 ↔ 2) oznacza to samo wyrażenie co poprzednio, ale z zamienionymi indeksami 1 i 2.

Zastosowania w fizyce

Zerowa granica temperatury

W tym limicie $Matsubary$ jest równoważne całkowaniu urojonej częstotliwości na urojonej osi

${\ Displaystyle {\ Frac {1} {\ beta}} \ suma _ {i \ omega} = \ int _ {-i \ infty} ^ {i \ infty}} {\ Frac {\ operatorname {d} (i \ omega )}{2\pi i}}.}$

Niektóre całki nie są zbieżne. Należy je uregulować $\rightarrow \infty }$ wprowadzając odcięcie częstotliwości $}$ a następnie odejmując część rozbieżną ( $-zależną$ ) od całki przed przyjęciem granicy ${\ displaystyle \ Omega$ . Na przykład energię swobodną uzyskuje się przez całkę z logarytmu,

${\ Displaystyle \ eta \ lim _ {\ Omega \ rightarrow \ infty} \ lewo [\ int _ {-i \ Omega} ^ {i \ Omega}} {\ Frac {\ operatorname {d} (ja \omega )}{2\pi i}}\left(\ln(-i\omega +\xi)-{\frac {\pi \xi}}{2\Omega}}\right)-{\frac {\ Omega }{\pi }}(\ln \Omega -1)\right]=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta \xi &\xi < 0,\koniec{tablica}}\prawo.}$

co oznacza, że ​​w temperaturze zerowej energia swobodna odnosi się po prostu do energii wewnętrznej poniżej potencjału chemicznego. Również funkcję dystrybucji uzyskuje się za pomocą następującej całki

${\ Displaystyle \ eta \ lim _ {\ Omega \ rightarrow \ infty} \ int _ {-i \ Omega} ^ {i \ Omega}} {\ Frac {\ operatorname {d} (i \ omega)} 2 \ pi i}}\left({\frac {1}{-i\omega +\xi}}-{\frac {\pi}}{2\Omega}}\right)=\left\{{\begin{tablica} {cc}0&\xi \geq 0,\\-\eta &\xi <0,\end{tablica}}\right.}$

który pokazuje zachowanie funkcji skokowej w temperaturze zerowej.

Związane z funkcją Greena

Dziedzina czasu

Rozważmy funkcję G ( τ ) zdefiniowaną na wyimaginowanym przedziale czasu (0, β ). Można to podać w postaci szeregu Fouriera,

${\ Displaystyle G (\ tau) = {\ Frac {1} {\ beta}} \ suma _ {i \ omega} G (i\omega )e^{-i\omega \tau },}$

gdzie częstotliwość przyjmuje tylko dyskretne wartości oddalone od siebie o 2 π / β .

Konkretny wybór częstotliwości zależy od warunku brzegowego funkcji G ( τ ). W fizyce G ( τ ) oznacza urojoną reprezentację funkcji Greena w czasie

${\ Displaystyle G (\ tau) = - \ langle {\ mathcal {T}} _ {\ tau} \ psi (\ tau) \ psi ^ {*} (0) \ rangle.}$

Spełnia okresowy warunek brzegowy G ( τ + β )= G ( τ ) dla pola bozonowego. Natomiast dla pola fermionowego warunek brzegowy jest antyokresowy G ( τ + β ) = − G ( τ ).

Biorąc pod uwagę funkcję Greena G ( iω ) w dziedzinie częstotliwości, jej urojoną reprezentację czasu G ( τ ) można ocenić za pomocą sumowania częstotliwości Matsubary. W zależności od sumowanych częstotliwości bozonu lub fermionu wynikowe G ( τ ) może być różne. Rozróżnić, zdefiniować

${\ Displaystyle G_ {\ eta} (\ tau) = {\ rozpocząć {przypadki} G_{\rm {B}}(\tau ),&{\text{jeśli }}\eta =+1,\\G_{\rm {F}}(\tau ),&{\text{jeśli }} \eta =-1,\end{przypadki}}}$

z

${\ Displaystyle G _ {\ rm {B}} (\ tau) = {\ Frac {1} {\ beta }}\suma _{i\omega _{n}}G(i\omega _{n})e^{-i\omega _{n}\tau },}$

${\ Displaystyle G _ {\ rm {F}} (\ tau) = {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {m}} G (i \ omega _ {m}) e ^{-i\omega _{m}\tau}.}$

Zauważ, że τ jest ograniczone w głównym przedziale (0, β ). Warunek brzegowy można wykorzystać do rozszerzenia G ( τ ) poza główny przedział. Niektóre często używane wyniki podsumowano w poniższej tabeli.

${\ Displaystyle G (i \ omega)}$	${\ Displaystyle G _ {\ eta} (\ tau)}$
${\ Displaystyle (i \ omega - \ xi) ^ {- 1}}$	${\ Displaystyle -e ^ {\ xi (\ beta - \ tau)} n_ {\ eta} (\ xi)}$
${\ Displaystyle (i \ omega - \ xi) ^ {- 2}}$	${\ Displaystyle e ^ {\ xi (\ beta - \ tau)} n_ {\ eta} (\ xi) \ lewo (\tau +\eta \beta n_{\eta}(\xi)\right)}$
${\ Displaystyle (i \ omega - \ xi) ^ {- 3}}$	${\ Displaystyle - {\ Frac {1} {2}} e ^ {\ xi (\ beta - \ tau)} n _ {\ eta} (\ xi) \ lewo (\ tau ^ {2} + \ eta \ beta (\beta +2\tau )n_{\eta }(\xi )+2\beta ^{2}n_{\eta }^{2}(\xi )\right)}$
${\ Displaystyle (i \ omega - \ xi _ {1}) ^ {- 1} (i \ omega - \ xi _ {2}) ^{-1}}$	${\ Displaystyle - {\ Frac {e ^ {\ xi _ { 1}(\beta -\tau )}n_{\eta }(\xi _{1})-e^{\xi _{2}(\beta -\tau )}n_{\eta }(\xi _ {2})}{\xi _{1}-\xi _{2}}}}$
${\ Displaystyle (\ omega ^ {2} + m ^ {2}) ^ {- 1}}$	${\ Displaystyle {\ Frac {e ^ {-m \ tau}} {2m}} + {\ Frac {\ eta} {m}} \cosh {m\tau}\;n_{\eta}(m)}$
${\ Displaystyle i \ omega (\ omega ^ {2} + m ^ {2}) ^ {- 1}}$	${\ Displaystyle {\ Frac {e ^ {-m \ tau}} {2}} - \ eta \ \ sinh {m \ tau} \; n_{\eta}(m)}$

Efekt zmiany operatora

Mały wyimaginowany czas odgrywa tutaj kluczową rolę. Kolejność operatorów zmieni się, jeśli mały wyimaginowany czas zmieni znak.

${\ Displaystyle \ langle \ psi \ psi ^ {*} \ rangle = \ langle {\ mathcal {T}} _ {\ tau} \ psi (\ tau = 0 ^ {+}) \ psi ^ {*} (0 )\rangle =-G_{\eta }(\tau =0^{+})=-{\frac {1}{\beta }}\sum _{i\omega }G(i\omega)e^{ -i\omega 0^{+}}}$

${\ Displaystyle \ langle \ psi ^ {*} \ psi \ rangle = \ eta \ langle {\ mathcal {T}} _ {\ tau} \ psi (\ tau = 0 ^ {-})\psi ^{*}(0)\rangle =-\eta G_{\eta }(\tau =0^{-})=-{\frac {\eta }{\beta }}\sum _{i\omega }G(i\omega )e^{i\omega 0^{+}}}$

Funkcja dystrybucyjna

Ocena funkcji dystrybucji staje się trudna z powodu nieciągłości funkcji Greena G ( τ ) przy τ = 0. Aby ocenić sumowanie

${\ Displaystyle G (0) = \ suma _ {i \ omega} (i \ omega - \ xi) ^ {- 1},}$

oba wybory funkcji ważącej są dopuszczalne, ale wyniki są różne. Można to zrozumieć, jeśli nieco odsuniemy G ( τ ) od τ = 0, a następnie, aby kontrolować zbieżność, musimy przyjąć ${\ Displaystyle h _ {\ eta} ^ {(1) } (z)}$ jako funkcja ważenia dla ${\ Displaystyle G (\ tau = 0 ^ {+})}$ i ${\ Displaystyle h _ {\ eta} ^ {(2)} (z)}$ dla ${\ Displaystyle G (\ tau = 0 ^ {-})}$ .

Bozony

${\ Displaystyle G _ {\ rm {B}} (\ tau = 0 ^ { -})={\frac {1}{\beta}}\sum _{i\omega _{n}}{\frac {e^{i\omega _{n}0^{+}}}{i \omega _{n}-\xi }}=-n_{\rm {B}}(\xi ),}$

${\ Displaystyle G _ {\ rm {B}} (\ tau = 0 ^ {+}) = {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {n}} {\ Frac {e ^{-i\omega _{n}0^{+}}}{i\omega _{n}-\xi}}=-(n_{\rm {B}}(\xi)+1).}$

Fermiony

$}}=n_{\rm {F}}(\xi),}$

${\ Displaystyle G _ {\ rm {F}} (\ tau = 0 ^ {- })={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{i\omega _{m}0^{+}}}{i\ omega _{m}-\$

${\ Displaystyle G _ {\ rm {F}} (\ tau = 0 ^ {+}) = {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {m}} {\ Frac {e ^{-i\omega _{m}0^{+}}}{i\omega _{m}-\xi}}=-(1-n_{\rm {F}}(\xi)).}$

Darmowa energia

Bozony

${\ Displaystyle {\ Frac {1} {\ beta}} \ suma _ {i\omega _{n}}\ln(\beta (-i\omega _{n}+\xi))={\frac {1}{\beta}}\ln(1-e^{-\ beta \xi }),}$

Fermiony

${\ Displaystyle - {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {m}} \ ln (\ beta (-i \ omega _ {m} + \ xi}) = - {\ frac {1}{\beta}}\ln(1+e^{-\beta \xi}).}$

Oceny diagramów

Często spotykane diagramy są oceniane tutaj z ustawieniem trybu pojedynczego. Do problemów z wieloma trybami można podejść za pomocą całki funkcji widmowej.

Energia własna Fermiona

${\ Displaystyle \ Sigma (i \ omega _ {m}) = - {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {n}} {\ Frac {1} {i \ omega _ {m}+i\omega _{n}-\varepsilon }}{\frac {1}{i\omega _{n}-\Omega }}=-{\frac {n_{\rm {B}}( \varepsilon )+n_{\rm {F}}(\Omega)}{i\omega _{m}-\varepsilon +\Omega}}.}$

Pęcherzyk dziury cząstek

${\ Displaystyle \ Pi (i \ omega _ {n}) = {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {m}}} {\ Frac {1} {i \ omega _ { m}+i\omega _{n}-\varepsilon }}{\frac {1}{i\omega _{m}-\varepsilon '}}={\frac {n_{\rm {B}}(\ varepsilon )+n_{\rm {F}}\left(\varepsilon '\right)}{i\omega _{n}-\varepsilon +\varepsilon '}}.}$

Bąbel cząstek-cząstek

${\ Displaystyle \ Pi (i \ omega _ {n}) = - {\ Frac {1} {\ beta}} \ suma _ {i \ omega _ {m}}} {\ Frac {1} {i \ omega _ {m}+i\omega _{n}-\varepsilon }}{\frac {1}{-i\omega _{m}-\varepsilon '}}={\frac {1-n_{\rm {F }}\left(\varepsilon '\right)+n_{\rm {B}}(\varepsilon )}{i\omega _{n}-\varepsilon -\varepsilon '}}.}$

Dodatek: Własności funkcji dystrybucji

Funkcje dystrybucji

Ogólny zapis $eta}}$ funkcję rozkładu Bosego ( η = +1) lub Fermiego ( η = −1) n \ Displaystyle n_ { \

${\ Displaystyle n _ {\ eta} (\ xi) = {\ Frac {1} {e ^ {\ beta \ xi} - \ eta}}.}$

Jeśli to konieczne, specjalne oznaczenia n _B i n _F są używane do wskazania odpowiednio funkcji rozkładu Bosego i Fermiego

${\ Displaystyle n_ {\ eta} (\ xi) = {\ rozpocząć {przypadki} n_{\rm {B}}(\xi),&{\text{jeśli}}\eta =+1,\\n_{\rm {F}}(\xi),&{\text{jeśli }} \eta =-1.\end{przypadki}}}$

Związek z funkcjami hiperbolicznymi

Funkcja rozkładu Bosego jest powiązana z hiperboliczną funkcją cotangens przez

${\ Displaystyle n _ {\ rm {B}} (\ xi) = {\ Frac {1} {2}} \ lewo (\ operatorname {coth} {\ Frac {\ beta \ xi} {2}} -1 \ Prawidłowy).}$

Funkcja dystrybucji Fermiego jest powiązana z hiperboliczną funkcją styczną przez

${\ Displaystyle n _ {\ rm {F}} (\ xi) = {\ Frac {1} {2}} \ lewo (1- \ nazwa operatora {tanh} {\ Frac {\ beta \ xi} {2}} \ Prawidłowy).}$

Parytet

Obie funkcje dystrybucji nie mają określonej parzystości,

${\ Displaystyle n_ {\ eta} (- \ xi) = - \ eta -n_ {\ eta} (\ xi).}$

Inna formuła dotyczy funkcji $\ displaystyle c_ {\ eta}}$

${\ Displaystyle n_ {\ eta} (- \ xi) = n _ {\ eta} (\ xi) + 2 \ xi c_ {\ eta} (0, \ xi).}$

Jednak ich pochodne mają określoną parzystość.

Transmutacja Bosego-Fermiego

Funkcje dystrybucji Bosego i Fermiego ulegają transmutacji pod wpływem przesunięcia zmiennej o częstotliwość fermionową,

${\ Displaystyle n_ {\ eta} (i \ omega _ {m} + \ xi) = - n_ {- \ eta} (\ xi).}$

Jednak przesuwanie o częstotliwości bozonowe nie robi żadnej różnicy.

Pochodne

Pierwsze zamówienie

${\ Displaystyle n _ {\ rm {B}} ^ {\ pierwsza} (\ xi) = - {\ Frac {\ beta} {4 }}\mathrm {csch} ^{2}{\frac {\beta \xi}}{2}},}$

${\ Displaystyle n _ {\ rm {F}} ^ {\ pierwsza} (\ xi) = - {\ Frac {\ beta} {4}} \ operatorname {sech} ^ {2} {\ Frac {\ beta \ xi }{2}}.}$

Pod względem produktu:

${\ Displaystyle n_ {\ eta} ^ {\ pierwsza} (\ xi) = - \ beta n_ {\ eta} (\ xi) (1 + \ eta n_ {\ eta} (\ xi)).}$

W temperaturze zerowej:

${\ Displaystyle n _ {\ eta} ^ {\ pierwsza} (\ xi) = \ eta \ delta (\ xi) {\ tekst {jak}} \ beta \ rightarrow \ infty.}$

Drugie zamówienie

${\ Displaystyle n _ {\ rm {B}} ^ {\ pierwsza \ pierwsza} (\ xi) = {\ Frac { \beta ^{2}}{4}}\operatorname {csch} ^{2}{\frac {\beta \xi }{2}}\operatorname {coth} {\frac {\beta \xi }{2} },}$

${\ Displaystyle n _ {\ rm {F}} ^ {\ pierwsza \ pierwsza} (\ xi) = {\ Frac {\ beta ^ {2}} {4}} \ nazwa operatora {sech} ^ {2} {\ frac {\ beta \ xi }{2}} \ nazwa operatora {tanh} {\ frac {\ beta \ xi }{2}}.}$

Formuła różnicy

${\ Displaystyle n_ {\ eta} (a + b) -n _ {\ eta} (ab) = - {\ Frac {\ operatorname {sinh} \ beta b} {\ operatorname {cosh} \ beta a - \ eta \ ,\mathrm {cosh} \beta b}}.}$

Przypadek a = 0

${\ Displaystyle n _ {\ rm {B}} (b) -n _ {\ rm {B}} (-b) = \ mathrm {coth} {\ Frac {\ beta b} {2}},}$

${\ Displaystyle n _ {\ rm {F}} (b) -n _ {\ rm {F}} (-b) = - \ operatorname {tanh} {\ Frac {\ beta b} {2}}.}$

Przypadek a → 0

${\ Displaystyle n _ {\ rm {B}} (a + b) -n_{\rm {B}}(ab)=\operatorname {coth} {\frac {\beta b}{2}}+n_{\rm {B}}^{\prime \prime }(b)a ^{2}+\cdots ,}$

${\ Displaystyle n _ {\ rm {F}} (a + b) -n _ {\ rm {F}} (ab) = - \ operatorname {tanh} {\ Frac {\ beta b} {2}} + n_ { \rm {F}}^{\prime \prime }(b)a^{2}+\cdots .}$

Przypadek b → 0

${\ Displaystyle n _ {\ rm {B}} (a + b) -n _ {\ rm {B }}(ab)=2n_{\rm {B}}^{\prime }(a)b+\cdots ,}$

${\ Displaystyle n _ {\ rm {F}} (a + b) -n _ {\ rm {F}} (ab) = 2n _ {\ rm {F}} ^ {\ pierwsza} (a) b + \ cdots.}$

Funkcja c _η

Definicja:

${\ Displaystyle c_ {\ eta} (a, b) \ równoważnik - {\ Frac {n_ {\ eta} (a + b) -n_ {\ eta} (ab)} {2b}}.}$

Dla typu Bose i Fermi:

$\ Displaystyle c _ {\ rm {B}} (a, b) \ równoważnik c_ {+} (a, b)}$

${\ Displaystyle c_ {\ rm {F}} (a, b) \ równoważnik c_ {-} (a, b).}$

Związek z funkcjami hiperbolicznymi

${\ Displaystyle c_ {\ eta} (a, b) = {\ Frac {\ sinh \ beta b} {2b (\ cosh \ beta a- \ eta \ cosh \ beta b)}}.}$

Jest $_$ _

Aby uniknąć przepełnienia w obliczeniach numerycznych, używane są funkcje tanh i coth

${\ Displaystyle c _ {\ rm {B}} (a, b) = {\frac {1}{4b}}\left(\operatorname {coth} {\frac {\beta (ab)}{2}}-\operatorname {coth} {\frac {\beta (a+b)} {2}}\right),}$

${\ Displaystyle c _ {\ rm {F}} (a, b) = {\ Frac {1} {4b}} \ lewo (\ nazwa operatora {tanh} {\ Frac {\ beta (a + b)} {2} }-\operatorname {tanh} {\frac {\beta (ab)}{2}}\right).}$

Przypadek a = 0

${\ Displaystyle c _ {\ rm {B}} (0, b) = - {\ Frac {1} {2b}} \ operatorname {coth} {\ Frac {\ beta b} {2}},}$

${\ Displaystyle c _ {\ rm {F}} (0, b) = {\ Frac {1} {2b}} \ operatorname {tanh} {\ Frac {\ beta b} {2}}.}$

Przypadek b = 0

${\ Displaystyle c _ {\ rm {B}} (a, 0) = {\ Frac {\ beta} {4}} \ operatorname {csch} ^ {2}{\frac {\beta a}{2}},}$

${\ Displaystyle c _ {\ rm {F}} (a, 0) = {\ Frac {\ beta} {4}} \ operatorname {sech} ^ {2} {\ Frac {\ beta a} {2}}. }$

Dolna granica temperatury

Dla a = 0: ${\ Displaystyle c_ {\ rm {F}} (0, b) = {\ Frac {1} {2 | b|}}.}$

Dla b = 0: ${\ Displaystyle c _ {\ rm {F}} (a, 0) = \ delta (a).}$

Ogólnie,

${\ Displaystyle c_ {\ rm {F}} (a, b) = {\ rozpocząć {przypadki} {\ Frac {1} {2 | b|}}, & {\ tekst {jeśli}} | a | <| b|\\0,&{\text{jeśli }}|a|>|b|\end{przypadki}}}$

Zobacz też

• Wyimaginowany czas
• Kwantowa teoria pola termicznego

Linki zewnętrzne

Agustin Nieto: Ocena sum na częstotliwościach Matsubara . arXiv:hep-ph/9311210

Repozytorium Github: MatsubaraSum Pakiet Mathematica do sumowania częstotliwości Matsubara.

A. Taheridehkordi, S. Curnoe, JPF LeBlanc: Algorytmiczna integracja Matsubara dla modeli podobnych do Hubbarda. . arXiv:cond-mat/1808.05188