Estymator minimaksu

W statystycznej teorii decyzji , gdzie mamy do czynienia z problemem oszacowania deterministycznego parametru (wektora) ${\ Displaystyle \ theta \ in \ Theta}$ na podstawie obserwacji ${\ Displaystyle x \ in {\ mathcal {X }},}$ estymator (reguła estymacji) nazywa się minimaksem , jeśli jego maksymalne ryzyko jest minimalne wśród wszystkich estymatorów $Displaystyle \ theta \, \$$M {$ } . W pewnym sensie oznacza to, że $estymatorem , który$ najlepiej w najgorszym możliwym przypadku dozwolonym w problemie.

Konfiguracja problemu

$lub$ problem oszacowania deterministycznego (nie $danych$ parametru na podstawie uszkodzonych rozkład prawdopodobieństwa warunkowego ${\ Displaystyle P (x \ mid \ theta) \ \!}$ . Naszym celem jest znalezienie „dobrego” estymatora ${\ Displaystyle \ delta (x) \, \!}$ do oszacowania parametru , który minimalizuje pewną daną funkcję ryzyka ${\ Displaystyle R (\ theta, \ delta) \, \$$!$ . Tutaj funkcja ryzyka (technicznie rzecz biorąc, $ponieważ$ lub operator , jest funkcją funkcji, a NIE składem funkcji) jest oczekiwaniem pewnej funkcji straty ${\ Displaystyle L (\ theta, \ delta) \, \!}$ w odniesieniu do ${\ Displaystyle P (x \ mid \ theta) \, \!$ } $delta) = \|\ theta - \ delta \|^ {2} \,\!}$ \ , a funkcją ryzyka dla tej straty jest błąd średniokwadratowy (MSE).

Niestety, generalnie ryzyka nie można zminimalizować, ponieważ zależy ono od samego nieznanego parametru (Gdybyśmy wiedzieli, jaka jest rzeczywista wartość $\ displaystyle \ theta \,$$!}$ , nie musielibyśmy tego szacować). Dlatego wymagane są dodatkowe kryteria znalezienia estymatora optymalnego w pewnym sensie. Jednym z takich kryteriów jest kryterium minimax.

Definicja

Definicja : Estymator nazywa się minimaksem w odniesieniu do funkcji ryzyka ${\ Displaystyle R (\ theta, \ delta) \, \!}$${\ Displaystyle \ delta ^ {M}: {\ mathcal {X}} \ rightarrow \ Theta \, \!}$ jeśli osiąga najmniejsze maksymalne ryzyko spośród wszystkich estymatorów, co oznacza, że ​​​​spełnia

${\ Displaystyle \ sup _ {\ theta \ in \ Theta} R (\ theta, \ delta ^ {M}) = \ inf _ {\ delta} \ sup _ {\ theta \ in \ Theta} R (\ theta, \delta ).\,}$

Najmniej korzystna dystrybucja

Logicznie rzecz biorąc, estymator jest minimaksem, gdy jest najlepszy w najgorszym przypadku. Kontynuując $rozkładu$ ​​​​logikę, estymator minimaksu powinien być estymatorem Bayesa w odniesieniu do najmniej korzystnego wcześniejszego . $, \!}$ zademonstrować to pojęcie, oznacz średnie ryzyko estymatora Bayesa $\ delta _ {\ pi} \$ \ Displaystyle

${\ Displaystyle R _ {\ pi} = \ int R (\ teta, \ delta _ {\ pi}) \, d \ pi (\ teta) \ ,}$

$średnie$ : Wcześniejsza dystrybucja $najmniej$ korzystną, jeśli dla każdej innej dystrybucji ryzyko spełnia ${\ styl wyświetlania r_{\pi}\geq r_{\pi '}\,}$ .

Twierdzenie 1: Jeśli ${\ Displaystyle R _ {\ pi} = \ sup _ {\ teta} R (\ teta, \ delta _ {\ pi}), \,}$ Następnie:

1. ${\ Displaystyle \ delta _ {\ pi} \, \!}$ To minimaks.
2. Jeśli $,$ jest to również unikalny estymator minimax.
3. ${\ Displaystyle \ pi \, \!}$ jest najmniej korzystne.

Wniosek: jeśli estymator Bayesa ma stałe ryzyko, jest to minimaks. Pamiętaj, że nie jest to warunek konieczny.

Przykład 1: Nieuczciwa moneta: rozważ problem oszacowania wskaźnika „sukcesu” zmiennej dwumianowej x $\ Displaystyle x \ sim B (n, \ theta) \, \!}$ . Można to postrzegać jako oszacowanie szybkości, z jaką nieuczciwa moneta spada na „reszki” lub „reszki”. W tym przypadku estymator Bayesa względem a Beta , $_$ _

${\ Displaystyle \ delta ^ {M} = {\ Frac {x + 0,5 {\ sqrt {n}}} {n + {\ sqrt {n}}}}, \, }$

ze stałym ryzykiem Bayesa

${\ Displaystyle R = {\ Frac {1} {4 (1 + {\ sqrt {n}}) ^ {2}}} \,}$

i zgodnie z Wnioskiem jest minimaksem.

Definicja: Sekwencja wcześniejszych dystrybucji $nazywana$ jest najmniej korzystną, jeśli dla jakiejkolwiek innej dystrybucji $\ Displaystyle \ pi '\, \$ }

${\ Displaystyle \ lim _ {n \ rightarrow \ infty} r _ {\ pi _ {n}} \ geq r_ {\ pi '}. \,}$

${\ Displaystyle \ sup _ {\ teta} R (\ teta, \ delta) = \ lim _ {n \ strzałka w prawo \ infty} r_ {\ pi _ {n}} \, \! }$ : Jeśli istnieje sekwencja a priori $że$ taki , $,$ , a następnie:

1. ${\ Displaystyle \ delta \, \!}$ to minimaks.
2. Sekwencja jest najmniej korzystna. ${\ displaystyle \ pi _ {n} \, \!}$

Zauważ, że żadna wyjątkowość nie jest tutaj gwarantowana. Na przykład estymator ML z poprzedniego przykładu można osiągnąć jako granicę estymatorów Bayesa w odniesieniu do jednolitego wcześniejszego , ${\ Displaystyle \ pi _ {n} \ sim U [- n, n] \, \!}$ z rosnącym wsparciem, a także w odniesieniu do zerowej średniej normalnej wcześniejszej ${\ Displaystyle \ pi _ {n} \ sim N (0, n \ sigma ^{2})\,\!}$ z rosnącą wariancją. Tak więc ani wynikowy estymator ML nie jest unikalnym minimaksem, ani najmniej korzystny wcześniejszy nie jest unikalny.

Przykład 2: Rozważ problem oszacowania średniej $x$ wektora losowego Gaussa $\ Displaystyle x \ sim N (\ theta, I_ { p}\sigma ^{2})\,\!}$ . Estymator największej wiarygodności (ML) dla w tym przypadku to po prostu $ML}} = x \, \!}$$\ Displaystyle \ delta _ {\ tekst$ , a jego ryzyko jest

${\ Displaystyle R (\ teta, \ delta _ {\ tekst {ML}}) = E {\|\ delta _ {ML} - \ teta \|^ {2}} = \ suma _ {i = 1} ^ {p}E(x_{i}-\theta_{i})^{2}=p\sigma ^{2}.\,}$

MSE estymatora największej wiarygodności a estymator Jamesa-Steina

Ryzyko jest stałe, ale estymator ML w rzeczywistości nie jest estymatorem Bayesa, więc wniosek z twierdzenia 1 nie ma zastosowania. Jednak estymator ML jest granicą estymatorów Bayesa w odniesieniu do wcześniejszej sekwencji ${\ Displaystyle \ pi _ {n} \ sim N (0, n \ sigma ^ {2} )\,\!}$ , a zatem rzeczywiście minimax zgodnie z Twierdzeniem 2. Niemniej jednak minimaxity nie zawsze implikuje dopuszczalność . W rzeczywistości w tym przykładzie wiadomo, że estymator ML jest niedopuszczalny (niedopuszczalny), gdy ${\ displaystyle p> 2 \, \!$ } Słynny $,$ Jamesa-Steina w ML . Chociaż oba estymatory mają to samo ryzyko , gdy ${\ Displaystyle \|\ theta \|\ rightarrow \ infty$$}$ \ i oba są minimaksem, estymator Jamesa-Steina ma mniejsze ryzyko dla dowolnego skończonego ${\ Displaystyle \|\ theta \|\, \!$ } Fakt ten ilustruje poniższy rysunek.

Kilka przykładów

Na ogół wyznaczenie estymatora minimaksu jest trudne, a często wręcz niemożliwe. Niemniej jednak w wielu przypadkach wyznaczono estymator minimaksu.

Przykład 3: Ograniczona średnia normalna: podczas szacowania średniej wektora normalnego ${\ Displaystyle x \ sim N (\ theta, I_ {n} \ sigma ^ {2}) \, \!}$ , gdzie wiadomo, że ${\ Displaystyle \|\ theta \|^ {2} \ równoważnik M \, \!$ } Wiadomo, że estymator Bayesa względem a priori, który jest równomiernie rozłożony na krawędzi ograniczającej sfery , jest minimaksem, gdy ${\ Displaystyle M \ równoważnik n \, \!}$ . Wyrażenie analityczne dla tego estymatora to

${\ Displaystyle \ delta ^ {M} (x) = {\ Frac {MJ_ {n +1}(M\|x\|)}{\|x\|J_{n}(M\|x\|)}}x,\,}$

gdzie $Bessela$ zmodyfikowaną pierwszego . _ _

Asymptotyczny estymator minimax

Trudność w określeniu dokładnego estymatora minimaksu zmotywowała badanie estymatorów asymptotycznego minimaksu - estymator $się$ -asymptotyczny $przybliżony$ ) minimaks,

${\ Displaystyle \ sup _ {\ theta \ in \ Theta} R (\ theta, \ delta ') \ równoważnik c \ inf _ {\ delta} \ sup _ {\ theta \ in \ Theta} R (\ theta, \ delta ).}$

Dla wielu problemów estymacji, zwłaszcza w ustawieniach estymacji nieparametrycznej, ustalono różne przybliżone estymatory minimax. Projekt przybliżonego estymatora minimaksu jest ściśle powiązany z geometrią, taką jak metryczna liczba entropii, ${\ displaystyle \ Theta}$ .

Randomizowany estymator minimax

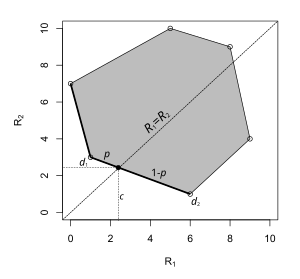
Czasami estymator minimaksu może przybrać postać losowej reguły decyzyjnej . Przykład pokazano po lewej stronie. , a każdy punkt na wykresie odpowiada ryzyku reguły decyzyjnej: współrzędna x to ryzyko, gdy parametr wynosi θ 1 {\ displaystyle \ theta $}$ to ryzyko, gdy parametr wynosi ${\ displaystyle \ theta _ {2}}$ . W tym problemie decyzyjnym estymator minimaksu leży na odcinku łączącym dwa estymatory deterministyczne. Wybór $p {\ displaystyle \ delta _ {1}}$ z prawdopodobieństwem ${\ displaystyle 1-p}$ i $\ delta _ {2}}$$displaystyle$ z prawdopodobieństwem najwyższe ryzyko.

Związek z solidną optymalizacją

Solidna optymalizacja to podejście do rozwiązywania problemów optymalizacyjnych w warunkach niepewności przy znajomości podstawowych parametrów. Na przykład estymacja bayesowska MMSE parametru wymaga znajomości funkcji korelacji parametrów. Jeśli znajomość tej funkcji korelacji nie jest w pełni dostępna, popularnym podejściem do solidnej optymalizacji minimaksowej jest zdefiniowanie zbioru charakteryzującego niepewność funkcji korelacji, a następnie przeprowadzenie optymalizacji minimaksowej odpowiednio na zbiorze niepewności i estymatorze. Podobne optymalizacje minimax można zastosować, aby estymatory były odporne na pewne nieprecyzyjnie znane parametry. Na przykład ostatnie badanie dotyczące takich technik w obszarze przetwarzania sygnałów można znaleźć w.

W R. Fandom Noubiap i W. Seidel (2001) opracowano algorytm obliczania reguły decyzyjnej Gamma-minimaks, gdy Gamma jest dana przez skończoną liczbę uogólnionych warunków momentów. Taka reguła decyzyjna minimalizuje maksimum całek funkcji ryzyka w odniesieniu do wszystkich rozkładów w Gamma. Reguły decyzyjne gamma-minimaks są przedmiotem zainteresowania w badaniach odporności w statystyce bayesowskiej.

• EL Lehmann i G. Casella (1998), Theory of Point Estimation, wyd. Nowy Jork: Springer-Verlag.
• F. Perron i E. Marchand (2002), „O estymatorze minimaksu ograniczonej średniej normalnej”, Statistics and Probability Letters 58 : 327–333.
• R. Fandom Noubiap i W. Seidel (2001), „Algorytm obliczania reguł decyzyjnych Gamma-Minimax w warunkach uogólnionych momentów”, Annals of Statistics , sierpień 2001, tom. 29, nie. 4, s. 1094–1116
•    Stein, C. (1981). „Oszacowanie średniej wielowymiarowego rozkładu normalnego” . Roczniki statystyki . 9 (6): 1135–1151. doi : 10.1214/aos/1176345632 . MR 0630098 . Zbl 0476.62035 .