Falka Poissona

W matematyce, w analizie funkcjonalnej, kilka różnych falek jest znanych pod nazwą falka Poissona . W jednym kontekście termin „falka Poissona” jest używany do określenia rodziny falek oznaczonych zbiorem dodatnich liczb całkowitych , których członkowie są powiązani z rozkładem prawdopodobieństwa Poissona . Te falki zostały po raz pierwszy zdefiniowane i zbadane przez Karlene A. Kosanovich, Allana R. Mosera i Michaela J. Piovoso w latach 1995–96. W innym kontekście termin ten odnosi się do pewnej falki, która obejmuje postać jądra całkowego Poissona. W jeszcze innym kontekście terminologia jest używana do opisania rodziny złożonych falek indeksowanych dodatnimi liczbami całkowitymi, które są powiązane z pochodnymi jądra całkowego Poissona.

Falki związane z rozkładem prawdopodobieństwa Poissona

Definicja

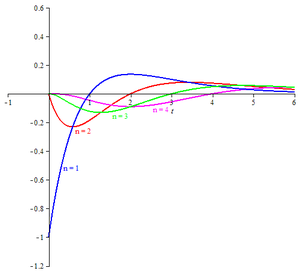
Członkowie rodziny falek Poissona odpowiadających n = 1, 2, 3, 4.

Dla każdej dodatniej liczby całkowitej n falka Poissona jest zdefiniowana przez ${\ Displaystyle \ psi _ {n} (t)}$

${\ Displaystyle \ psi _ {n} (t) = {\ rozpocząć {przypadki} \ lewo ({\frac {tn}{n!}}\right)t^{n-1}e^{-t}&{\text{dla}}t\geq 0\\0&{\text{dla}} t<0.\end{przypadki}}}$

Aby zobaczyć zależność między falką Poissona a rozkładem Poissona, niech X będzie dyskretną zmienną losową o rozkładzie Poissona z parametrem (średnia) t i dla każdej nieujemnej liczby całkowitej n niech Prob( X = n ) = p _n ( t ). Następnie mamy

${\ Displaystyle p_ {n} (t) = {\ Frac {t ^ {n}} {n!}} e ^ {-t}.}$

Falka Poissona jest teraz dana przez ${\ Displaystyle \ psi _ {n} (t)}$

${\ Displaystyle \ psi _ {n} (t) = - {\ Frac {d} {dt}} p_ {n} (t).}$

Podstawowe właściwości

• ${\ Displaystyle \ psi _ {n} (t)}$ jest wsteczną różnicą wartości rozkładu Poissona:

${\ Displaystyle \ psi _ {n} (t) = p_ {n} (t) -p_ {n-1} (t).} „$

• Falistość” członków tej rodziny falek wynika z

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} \ psi _ {n} (t) \, dt = 0.} Transformata Fouriera$

• ψ $\ Displaystyle \psi _{n}(t)}$ jest dane

${\ Displaystyle \ Psi (\ omega) = {\ Frac {-i \ omega}} {(1 + i \ omega) ^ {n + 1}}}.} Stała dopuszczalności$

• związana z ${\ Displaystyle \ psi _ {n} (t)}$ jest

${\ Displaystyle C _ {\ psi _ {n}} = \ int _ {- \ infty} ^ {\ infty} {\ Frac {\ lewo | \ Psi _ {n} (\ omega) \ prawo | ^ {2} }{|\omega |}}\,d\omega ={\frac {1}{n}}.}$

• Falka Poissona nie jest ortogonalną rodziną falek.

Transformata falkowa Poissona

Rodzinę falkową Poissona można wykorzystać do skonstruowania rodziny transformat falkowych Poissona funkcji zdefiniowanych w dziedzinie czasu. Ponieważ falki Poissona również spełniają warunek dopuszczalności, funkcje w dziedzinie czasu można zrekonstruować z ich transformat falkowych Poissona, używając wzoru na odwrotne transformaty falkowe w czasie ciągłym.

Jeśli f ( t ) jest funkcją w dziedzinie czasu, jej n -ta transformata falkowa Poissona jest dana wzorem

${\ Displaystyle (W_ {n} f) (a, b) = {\ Frac {1} {\ sqrt {| a|}}} \int _{-\infty }^{\infty}f(t)\psi _{n}\left({\frac {tb}{a}}\right)\,dt}$

W odwrotnym kierunku, biorąc pod uwagę n -tą transformatę falkową Poissona ${\ Displaystyle (W_ {n} f) (a, b)}$ funkcji fa ( t ) w dziedzinie czasu , funkcję f ( t ) można zrekonstruować w następujący sposób:

${\ Displaystyle f (t) = {\ Frac {1} {C _ {\ psi _ {n}}}} \ int _ {- \ infty} ^ {\ infty} \ lewo [\ int _ {- \ infty} ^{\infty}\,\left\{(W_{n}f)(a,b){\frac {1}{\sqrt {|a|}}}\psi _{n}\left({\ frac {tb}{a}}\right)\,\right\}db\right]{\frac {da}{a^{2}}}}$

Aplikacje

Transformaty falkowe Poissona zostały zastosowane w analizie wielorozdzielczej, identyfikacji systemu i estymacji parametrów. Są szczególnie przydatne w badaniu problemów, w których funkcje w dziedzinie czasu składają się z liniowych kombinacji zanikających wykładników z opóźnieniem czasowym.

Falka związana z jądrem Poissona

Obraz falki związanej z jądrem Poissona.

Obraz transformaty Fouriera falki związanej z jądrem Poissona.

Definicja

Falka Poissona jest zdefiniowana przez funkcję

${\ Displaystyle \ psi (t) = {\ Frac {1} {1} {\ pi}} {\ Frac {1-t ^ {2}} {(1+t^{2})^{2}}}}$

Można to wyrazić w postaci

${\ Displaystyle \ psi (t) = P (t) + t {\ Frac {d} {dt}} P (t)}$ gdzie ${\ Displaystyle P (t) = {\ Frac {1} {\ pi}} {\ Frac {1} {1} {1 + t ^ {2}}}}$ .

Związek z jądrem Poissona

Funkcja pojawia $się$ jako integralne jądro w pewnego problemu operatora Laplace'a .

To jest problem z wartością początkową: biorąc pod uwagę dowolną ${\ Displaystyle \ phi (x, y)}$$})}$ { $mathbb {$ Displaystyle zdefiniowane w górnej półpłaszczyźnie spełniającej następujące warunki:

1. $_$ _
2. ${\ Displaystyle \ phi (x, y) \ rightarrow s (x)}$ jak ${\ Displaystyle y \ rightarrow 0}$ w ${\ Displaystyle L ^ {p}(\mathbb {R} )}$ .

Problem ma następujące rozwiązanie: Istnieje dokładnie jedna funkcja spełniająca te dwa warunki i dana przez ${\ Displaystyle \ phi (x, y)}$

${\ Displaystyle \ phi (t, y) = P_ {y} (t) \ gwiazda s (t)}$

gdzie ${\ Displaystyle P_ {y} (t) = {\ Frac {1} {y}} P \ lewo ({\ frac {t}{y}}\right)={\frac {1}{\pi }}{\frac {y}{t^{2}+y^{2}}}} i gdzie "$ ⋆ $\ displaystyle \star }$ " oznacza operację splotu . P. ${\ Displaystyle P_ {y} (t)$ jest integralnym jądrem funkcji ${\ Displaystyle \ phi (x, y)}$ . Funkcja $)}$ harmoniczną kontynuacją $Displaystyle \ phi (x,$ górnej połowie płaszczyzny

Nieruchomości

• „Falistość” funkcji wynika z

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} \ psi (t) \, dt = 0}$ .

• Transformata Fouriera ${\ Displaystyle \ psi (t)}$ jest dana przez

${\ Displaystyle \ Psi (\ omega) = | \ omega | e ^ {- | \ omega |}}$ .

• Stała dopuszczalności to

${\ Displaystyle C _ {\ psi} = \ int _ {- \ infty} ^ {\ infty}} {\ Frac {\ lewo | \ Psi (\ omega) \ prawo | ^ {2}} {| \omega |}}\,d\omega =2.}$

Klasa złożonych falek związanych z jądrem Poissona

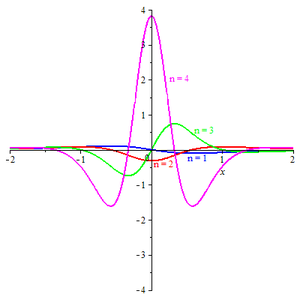
$}$ rzeczywistych części falki Poissona $=$ n $=$ .

Wykresy urojonych części falki Poissona ${\ Displaystyle \ psi _ {n} (t)}$ dla ${\ Displaystyle n = 1,2,3,4 }$ .

Definicja

Falka Poissona to rodzina funkcji o wartościach zespolonych indeksowanych przez zbiór dodatnich liczb całkowitych i zdefiniowanych przez

${\ Displaystyle \ psi _ {n} (t) = {\ Frac {1} {2 \ pi}} (1-to ) ^ {- (n + 1)}}$ gdzie ${\ Displaystyle n = 1,2,3, \ ldots}$

Związek z jądrem Poissona

Funkcję można wyrazić jako n -tą pochodną w następujący sposób: ${\ Displaystyle \ psi _ {n} (t)}$

${\ Displaystyle \ psi _ {n} (t) = {\ Frac {1} {2 \ pi}} {\ Frac {1} {n !\,i^{n}}}{\frac {d^{n}}{dt^{n}}}\left((1-it)^{-1}\right)}$

Zapisywanie funkcji ${\ Displaystyle (1-it) ^ {- 1}}$ w kategoriach jądra całkowego Poissona ${\ Displaystyle P (t) = {\frac {1}{1+t^{2}}}}$ jako

${\ Displaystyle (1-it) ^ {- 1} = P (t) + itP (t)}$

mamy

${\ Displaystyle \ psi _ {n} (t) = {\ Frac {1} {2 \ pi}} {\ Frac {1} {n! \, i ^ {n}}} {\ Frac {d ^ { n}}{dt^{n}}}P(t)+i\left({\frac {1}{2\pi}}{\frac {1}{n!\,i^{n}}} {\frac {d^{n}}{dt^{n}}}\left(tP(t)\right)\right)}$

Zatem można $funkcję$ Poissona.

Nieruchomości

Transformata Fouriera jest dana przez ${\ Displaystyle \ psi _ {n} (t)}$

${\ Displaystyle \ Psi _ {n} (\ omega) = {\ Frac {1} {\ Gamma (n + 1) }}\omega ^{n}e^{-\omega}u(\omega)}$

gdzie ${\ Displaystyle u (\ omega)}$ jest funkcją kroku jednostkowego .