Filtr adaptacyjny

Filtr adaptacyjny to system z filtrem liniowym , który ma funkcję przenoszenia kontrolowaną przez zmienne parametry i środki do regulacji tych parametrów zgodnie z algorytmem optymalizacji . Ze względu na złożoność algorytmów optymalizacji prawie wszystkie filtry adaptacyjne są filtrami cyfrowymi . W niektórych zastosowaniach wymagane są filtry adaptacyjne, ponieważ niektóre parametry pożądanej operacji przetwarzania (na przykład położenie powierzchni odbijających w przestrzeni pogłosowej ) nie są znane z góry lub ulegają zmianie. Filtr adaptacyjny z zamkniętą pętlą wykorzystuje sprzężenie zwrotne w postaci sygnału błędu, aby udoskonalić swoją funkcję przenoszenia.

Ogólnie rzecz biorąc, proces adaptacyjny w pętli zamkniętej obejmuje wykorzystanie funkcji kosztu , która jest kryterium optymalnej wydajności filtra, do zasilania algorytmu, który określa, jak zmodyfikować funkcję przenoszenia filtra, aby zminimalizować koszt w następnej iteracji. Najbardziej powszechną funkcją kosztu jest średnia kwadratowa sygnału błędu.

Wraz ze wzrostem mocy cyfrowych procesorów sygnałowych , filtry adaptacyjne stały się znacznie bardziej powszechne i są obecnie rutynowo stosowane w urządzeniach takich jak telefony komórkowe i inne urządzenia komunikacyjne, kamery i aparaty cyfrowe oraz medyczny sprzęt monitorujący.

Przykład zastosowania

Zapis bicia serca (EKG ) może zostać zakłócony przez zakłócenia z sieci elektrycznej . Dokładna częstotliwość mocy i jej harmoniczne mogą zmieniać się z chwili na chwilę.

Jednym ze sposobów usunięcia szumu jest filtrowanie sygnału za pomocą filtra wycinającego przy częstotliwości sieciowej i jej pobliżu, ale może to nadmiernie pogorszyć jakość EKG, ponieważ częstość bicia serca również prawdopodobnie miałaby składowe częstotliwości w zakresie odrzuconym.

Aby obejść tę potencjalną utratę informacji, można zastosować filtr adaptacyjny. Filtr adaptacyjny pobierałby dane wejściowe zarówno od pacjenta, jak iz sieci zasilającej, dzięki czemu byłby w stanie śledzić rzeczywistą częstotliwość szumu w miarę jego wahań i odejmować szum od nagrania. Taka adaptacyjna technika generalnie pozwala na filtr o mniejszym zakresie odrzucania, co oznacza w tym przypadku, że jakość sygnału wyjściowego jest dokładniejsza do celów medycznych.

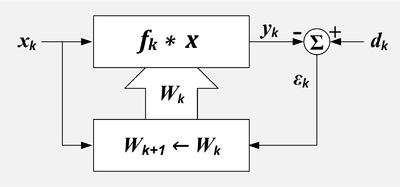
Schemat blokowy

Ideą filtra adaptacyjnego z zamkniętą pętlą jest to, że zmienny filtr jest dostosowywany do momentu, gdy błąd (różnica między wyjściem filtra a pożądanym sygnałem) zostanie zminimalizowany. Filtr najmniejszych średnich kwadratów (LMS) i filtr rekurencyjnych najmniejszych kwadratów (RLS) to typy filtrów adaptacyjnych.

Filtr adaptacyjny. k = numer próbki, x = wejście referencyjne, X = zbiór ostatnich wartości x, d = pożądane wejście, W = zbiór współczynników filtra, ε = wyjście błędu, f = odpowiedź impulsowa filtra, * = splot, Σ = suma, górne pole = filtr liniowy, dolne pole = algorytm adaptacyjny

Filtr adaptacyjny, zwarta reprezentacja. k = numer próbki, x = wejście referencyjne, d = żądane wejście, ε = wyjście błędu, f = odpowiedź impulsowa filtra, Σ = suma, box = filtr liniowy i algorytm adaptacyjny.

Istnieją dwa sygnały wejściowe do filtra adaptacyjnego: i $są$ czasami odpowiednio $wejściem$ wejściem referencyjnym . $resztkowy$ próbuje przefiltrować wejście odniesienia do repliki pożądanego wejścia, minimalizując sygnał . Gdy adaptacja się powiedzie, wyjście filtra $.$ oszacowaniem pożądanego sygnału

${\ displaystyle d_ {k}}$ , który obejmuje pożądany sygnał oraz niepożądane zakłócenia i

$obejmuje sygnały, które$ skorelowane z niektórymi niepożądanymi zakłóceniami w ${\ displaystyle d_ {} k}}$ .

k reprezentuje dyskretny numer próbki.

Filtr jest kontrolowany przez zestaw współczynników lub wag L+1.

$\ Displaystyle \ mathbf {W} _ {k} = \ lewo [w_ {0k}, \, w_ {1k}, \, ..., \, w_ {Lk} \ prawo] ^ {T}}$ reprezentuje zbiór lub wektor wag, które sterują filtrem w czasie próbkowania k.

gdzie odnosi $się$ do „ $.$ tym czasie

${\ Displaystyle \ mathbf {\ Delta W} _ {k}}$ reprezentuje zmianę wag, która następuje w wyniku korekt obliczonych w czasie próbkowania k.

Zmiany te zostaną zastosowane po czasie próbkowania k i przed ich użyciem w czasie próbkowania k+1.

Wyjście to zwykle ${\ displaystyle \ epsilon _ {k}}$ , ale może to być ${\ displaystyle y_ {k}}$ lub nawet współczynniki filtra. (Wdrow)

Sygnały wejściowe są zdefiniowane w następujący sposób:

${\ Displaystyle d_ {k} = g_ {k} + u_ {k} + v_ {k}}$

${\ styl wyświetlania x_{k}=g_{k}^{'}+u_{k}^{'}+v_{k}^{'}} gdzie: g = żądany sygnał,$

g

' =

sygnał skorelowany z pożądany sygnał g ,

u = sygnał niepożądany, który jest dodawany do g , ale nieskorelowany z g lub g '

u ' = sygnał, który jest skorelowany z sygnałem niepożądanym u , ale nieskorelowany z g lub g ' ,

v = an niepożądany sygnał (zwykle losowy szum) nieskorelowany z g , g ' , u , u ' lub v ' ,

v ' = niepożądany sygnał (zwykle losowy szum) nieskorelowany z g , g ' , u , u ' lub v .

Sygnały wyjściowe definiuje się w następujący sposób:

${\ Displaystyle y_ {k} = {\ kapelusz {g}} _ {k} + {\ kapelusz {u}} _ {k} + {\ kapelusz { v}} _ {k}}$

${\ Displaystyle \ epsilon _ {k} = d_ {k} -y_ {k}}$ .

gdzie:

${\ Displaystyle {\ hat {g}}}$ = wyjście filtra, jeśli wejście było tylko sol ' ,

${\ Displaystyle {\ hat {u}}}$ = wyjście filtra, jeśli wejście było tylko u ' ,

${\ Displaystyle {\ hat {v}}}$ = wyjście filtra, jeśli wejście było tylko v ' .

Filtr FIR z odczepioną linią opóźniającą

Jeśli filtr zmienny ma strukturę linii opóźniającej z odczepem skończonej odpowiedzi impulsowej (FIR) , wówczas odpowiedź impulsowa jest równa współczynnikom filtra. Wyjście filtra jest podane przez

${\ Displaystyle y_ {k} = \ suma _ {l = 0} ^ {L} w_ { lk}\ x_{(kl)}={\kapelusz {g}}_{k}+{\kapelusz {u}}_{k}+{\kapelusz {v}}_{k}}$

gdzie ${\ Displaystyle w_ {lk}}$ odnosi się do $' tej$ w k'tym czasie.

Idealny przypadek

W idealnym przypadku ${\ Displaystyle v \ równoważnik 0, v'\ równoważnik 0, g' \ równoważnik 0}$ . Wszystkie niepożądane sygnały w $displaystyle d_ {k}}$${\$ przez . ${\ displaystyle \ x_ {k}}$ składa się w całości z sygnału skorelowanego z niepożądanym sygnałem w ${\ displaystyle u_ {k}}$ .

Wyjście filtru zmiennego w idealnym przypadku wynosi

${\ Displaystyle y_ {k} = {\ kapelusz {u}} _ {k}}$ .

Sygnał błędu lub funkcja kosztu to różnica między ${\ displaystyle d_ {k}}$ i ${\ displaystyle y_ {k}}$

${\ Displaystyle \ epsilon _ {k} = d_ {k} -y_ {k} = g_ {k} + u_ {k} - {\ kapelusz {u}}_{k}}$ . Żądany sygnał gk przechodzi bez zmiany _.

Sygnał błędu ${$ zminimalizowany w sensie średniokwadratowym, gdy ${u}} _ {k }]}$ jest zminimalizowany. Innymi słowy, $}$ najlepszym oszacowaniem średniokwadratowym $u_ {k}$ . W idealnym przypadku ${\ Displaystyle u_ {k} = {\ kapelusz {u}} _ {k}}$ i ${\ Displaystyle \ epsilon _ {k} = g_ {k }}$ , a wszystko, co pozostaje po odejmowaniu, to $pożądany$ sygnał z usuniętymi wszystkimi niepożądanymi sygnałami.

Składowe sygnału na wejściu referencyjnym

$W$ sytuacjach wejście referencyjne składowe pożądanego sygnału. Oznacza to, że g' ≠ 0.

W tym przypadku nie jest możliwe idealne wyeliminowanie niepożądanych zakłóceń, ale możliwa jest poprawa stosunku sygnału do zakłóceń. Wyjście będzie

${\ Displaystyle \ epsilon _ {k} = d_ {k} -y_ {k} = g_ {k} - {\ kapelusz {g}}_{k}+u_{k}-{\kapelusz {u}}_{k}}$ . Żądany sygnał zostanie zmodyfikowany (zwykle zmniejszony).

Stosunek sygnału wyjściowego do zakłóceń ma prosty wzór określany jako inwersja mocy .

${\ Displaystyle \ rho _ {\ mathsf {out}} (z) = {\ Frac {1} {\ rho _ {\ mathsf {ref}} (z)}}}$ .

gdzie

${\ Displaystyle \ rho _ {\ mathsf {na zewnątrz}} (z) \}$ = stosunek sygnału wyjściowego do zakłóceń.

${\ Displaystyle \ rho _ {\ mathsf {ref}} (z) \}$ = stosunek sygnału odniesienia do interferencji.

${\ displaystyle z \}$ = częstotliwość w domenie z.

Ten wzór oznacza, że ​​stosunek sygnału wyjściowego do zakłóceń przy określonej częstotliwości jest odwrotnością stosunku sygnału odniesienia do zakłóceń.

Przykład: restauracja typu fast food ma okno podjazdowe. Przed wejściem do okienka klienci składają zamówienie, mówiąc do mikrofonu. Mikrofon wychwytuje również hałas silnika i otoczenia. Ten mikrofon zapewnia główny sygnał. Moc sygnału z głosu klienta i moc hałasu z silnika są równe. Pracownikom restauracji trudno jest zrozumieć klienta. Aby zmniejszyć ilość zakłóceń w głównym mikrofonie, drugi mikrofon jest umieszczony tam, gdzie ma zbierać dźwięki z silnika. Odbiera również głos klienta. Ten mikrofon jest źródłem sygnału odniesienia. W tym przypadku hałas silnika jest 50 razy silniejszy niż głos klienta. Po zbieżności układu anulującego stosunek sygnału głównego do zakłóceń zostanie poprawiony z 1:1 do 50:1.

Adaptacyjny łącznik liniowy

Adaptacyjny łącznik liniowy przedstawiający łącznik i proces adaptacji. k = numer próby, n = indeks zmiennej wejściowej, x = wejścia referencyjne, d = pożądane wejście, W = zbiór współczynników filtra, ε = błąd wyjściowy, Σ = suma, górne pole = sumator liniowy, dolne pole = algorytm adaptacyjny.

Adaptacyjny łącznik liniowy, zwarta reprezentacja. k = numer próbki, n = indeks zmiennej wejściowej, x = dane wejściowe referencyjne, d = żądane dane wejściowe, ε = wynik błędu, Σ = suma.

Adaptacyjny łącznik liniowy (ALC) przypomina adaptacyjny filtr FIR linii opóźniającej z odczepem, z tym wyjątkiem, że nie ma zakładanej zależności między wartościami X. Gdyby wartości X pochodziły z wyjść linii opóźniającej z odczepem, wówczas kombinacja odczepionej linii opóźniającej i ALC stanowiłaby filtr adaptacyjny. Jednak wartości X mogą być wartościami tablicy pikseli. Lub mogą to być wyjścia wielu odczepionych linii opóźniających. ALC znajduje zastosowanie jako adaptacyjny kształtownik wiązki dla układów hydrofonów lub anten.

${\ Displaystyle y_ {k} = \ suma _ {l = 0} ^ {L} w_ {lk} \ x_ {lk} = \ mathbf {W} _ {k} ^ {T} \ mathbf {x} _ {k}}$

gdzie ${\ Displaystyle w_ {lk}}$ odnosi się do ${\ displaystyle l}$ 'th wagi w k'th czas.

Algorytm LMS

Główny artykuł: Filtr najmniejszych średnich kwadratów

Jeśli filtr zmienny ma strukturę FIR z odczepioną linią opóźniającą, wówczas algorytm aktualizacji LMS jest szczególnie prosty. Zazwyczaj po każdej próbce współczynniki filtra FIR są dostosowywane w następujący sposób:(Widrow)

dla ${\ Displaystyle l = 0 \ kropki L}$

${\ Displaystyle w_ {l, k + 1} = w_ {lk} +2\mu \ \epsilon _{k}\ x_{kl}}$

μ nazywa się współczynnikiem zbieżności .

Algorytm LMS nie wymaga, aby wartości X miały jakiś szczególny związek; dlatego może być używany do adaptacji sumatora liniowego, jak również filtra FIR. W tym przypadku formuła aktualizacji jest zapisana jako:

${\ Displaystyle w_ {l, k + 1} = w_ {lk} + 2 \ mu \ \ epsilon _ {k} \ x_ {lk} }$

Efektem algorytmu LMS jest za każdym razem, k, dokonanie niewielkiej zmiany każdej wagi. Kierunek zmiany jest taki, że zmniejszyłby błąd, gdyby został zastosowany w czasie k. Wielkość zmiany każdej wagi zależy od μ, powiązanej wartości X i błędu w czasie k. Wagi, które mają największy udział w wynikach $.$ najczęściej zmieniane Jeśli błąd wynosi zero, nie powinno być żadnych zmian w wagach. Jeśli powiązana wartość X wynosi zero, zmiana wagi nie ma znaczenia, więc nie jest zmieniana.

Konwergencja

μ kontroluje, jak szybko i jak dobrze algorytm zbiega się do optymalnych współczynników filtra. Jeśli μ jest zbyt duże, algorytm nie będzie zbieżny. Jeśli μ jest zbyt małe, algorytm zbliża się powoli i może nie być w stanie śledzić zmieniających się warunków. Jeśli μ jest duże, ale nie za duże, aby zapobiec zbieżności, algorytm szybko osiąga stan ustalony, ale ciągle przekracza optymalny wektor wag. Czasami μ jest początkowo duże dla szybkiej zbieżności, a następnie zmniejszane, aby zminimalizować przeregulowanie.

Widrow i Stearns oświadczyli w 1985 r., że nie znają dowodu na to, że algorytm LMS będzie zbieżny we wszystkich przypadkach.

Jednak przy pewnych założeniach dotyczących stacjonarności i niezależności można wykazać, że algorytm będzie zbieżny, jeśli

gdzie

$^$ = suma całej mocy wejściowej

$sigma$

${\ Displaystyle \ sigma _ {l}}$ to wartość RMS ${ \displaystyle l}$ 'te wejście

W przypadku filtru z odczepem linii opóźniającej każde wejście ma taką samą wartość RMS, ponieważ są to po prostu te same wartości opóźnione. W tym przypadku całkowita moc wynosi

${\ Displaystyle \ sigma ^ {2} = (L + 1) \ sigma _ {0} ^ {2}}$

gdzie

jest ${\ Displaystyle \ sigma _ {0}}$ Wartość $strumienia$ .

Prowadzi to do znormalizowanego algorytmu LMS:

${\ Displaystyle w_ {l, k + 1} = w_ {lk} + \ lewo ({\ Frac {2 \ mu _ {\ sigma}} {\ sigma ^ {2}}} \ prawej) \ epsilon _ {k} \ x_ {kl}} w takim przypadku kryterium zbieżności przyjmuje postać: <$ μ $Displaystyle 0 <\ mu _ {\sigma <1}$ .

Nieliniowe filtry adaptacyjne

Celem filtrów nieliniowych jest przezwyciężenie ograniczeń modeli liniowych. Istnieje kilka powszechnie stosowanych podejść: Volterra LMS, filtr adaptacyjny jądra , filtr adaptacyjny Spline i filtr adaptacyjny Urysohn. Wielu autorów zalicza do tej listy również sieci neuronowe. Ogólną ideą stojącą za Volterra LMS i Kernel LMS jest zastąpienie próbek danych różnymi nieliniowymi wyrażeniami algebraicznymi. Dla Volterra LMS tym wyrażeniem jest seria Volterra . W Spline Adaptive Filter model jest kaskadą liniowego bloku dynamicznego i statycznej nieliniowości, która jest aproksymowana przez splajny. W filtrze adaptacyjnym Urysohn człony liniowe w modelu

${\ Displaystyle y_ {i} = \ suma _ {j = 0} ^ {m} w_ {j} \ x_ {ij}}$

są zastępowane fragmentarycznymi funkcjami liniowymi

${\ Displaystyle y_ {i} = \ suma _ {j = 0} ^ {m} f_ {j} (x_ {ij})}$

które są identyfikowane na podstawie próbek danych.

Zastosowania filtrów adaptacyjnych

• Redukcja szumów
• Przewidywanie sygnału
• Adaptacyjne anulowanie sprzężenia zwrotnego
• Redukcja szumów

Filtruj implementacje

• Filtr najmniejszych średnich kwadratów
• Rekurencyjny filtr najmniejszych kwadratów
• Filtr adaptacyjny w domenie częstotliwości bloków z wieloma opóźnieniami

Zobacz też

• Filtry adaptacyjne 2D
• Filtr (przetwarzanie sygnału)
• Filtr Kalmana
• Filtr adaptacyjny jądra
• Przewidywanie liniowe
• estymator MMSE
• filtr Wienera
• Równanie Wienera-Hopfa

Źródła

•   Hayes, Monson H. (1996). Statystyczne przetwarzanie i modelowanie sygnałów cyfrowych . Wileya. ISBN 978-0-471-59431-4 .
•   Haykin, Szymon (2002). Teoria filtrów adaptacyjnych . Sala Prentice'a. ISBN 978-0-13-048434-5 .
•   Wdowa, Bernard; Stearns, Samuel D. (1985). Adaptacyjne przetwarzanie sygnału . Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-004029-9 .