Jądro (przetwarzanie obrazu)

W przetwarzaniu obrazu jądro , macierz splotu lub maska to mała macierz używana do rozmycia, wyostrzania, wytłaczania, wykrywania krawędzi i nie tylko . Osiąga się to przez wykonanie splotu między jądrem a obrazem . Lub prościej, gdy każdy piksel w obrazie wyjściowym jest funkcją pobliskich pikseli (w tym samego siebie) w obrazie wejściowym, jądro jest tą funkcją.

Detale

Ogólnym wyrażeniem splotu jest

${\ Displaystyle g (x, y) = \ omega * f (x, y) = \ suma _ {dx = -a} ^ {a} {\ suma _ {dy = - b} ^ {b} {\ omega (dx,dy)f(x-dx,y-dy)}},}$

gdzie ${\ Displaystyle g (x, y)}$ to przefiltrowany obraz, ${\ Displaystyle f (x, y)}$ to oryginalny obraz, ${\ Displaystyle \ omega}$ jest jądrem filtra. Każdy element jądra filtra jest rozważany przez ${\ Displaystyle -a \ równoważnik dx \ równoważnik a}$ i ${\ Displaystyle -b \ równoważnik dy \ równoważnik b}$ .

W zależności od wartości pierwiastków, jądro może powodować szeroki zakres efektów. .

Operacja	Jądro ω	Wynik obrazu g(x,y)
Tożsamość	${\ Displaystyle {\ rozpocząć {bmatrix} \ \ 0&\ \ 0&\ \ 0\\\ \ 0&\ \ 1&\ \ 0\\\ \ 0&\ \ 0&\ \ 0\koniec {bmatrix}}}$
Wykrywanie grzbietu lub krawędzi	${\ Displaystyle {\ rozpocząć {bmatrix} 0 i -1 i 0 \\ -1 i \ \ 4 i -1 \\ 0 i -1 i 0 \ koniec {bmatrix}}}$
Wykrywanie grzbietu lub krawędzi	${\ Displaystyle {\ rozpocząć {bmatrix} -1 i -1 i -1 \\ -1 i \ \ 8 i -1 \\ -1 i -1 i - 1\koniec{bmacierz}}}$
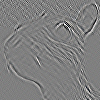
Wyostrzyć	${\ Displaystyle {\ rozpocząć {bmatrix} \ \ 0 i -1 i \ \ 0 \\ -1 i \ \ 5 i -1 \\\ \ 0 i -1 i \ \ 0 \ koniec { bmacierz}}}$
Rozmycie ramki ( znormalizowane )	${\ Displaystyle {\ Frac {1} {9}} {\ rozpocząć {bmatrix} \ \ 1 i \ \ 1 i \ \ 1 \\\ \ 1 i \ \ 1 i \ \ 1\\\ \ 1&\ \ 1&\ \ 1\end{bmacierz}}}$
Rozmycie gaussowskie 3 × 3 (przybliżenie)	${\ Displaystyle {\ Frac {1} {16}} {\ zacząć {bmatrix} \ \ 1 i \ \ 2 i \ \ 1 \\\ \ 2 i \ \ 4 i \ \ 2\\\ \ 1&\ \ 2&\ \ 1\koniec{bmacierz}}}$
Rozmycie gaussowskie 5 × 5 (przybliżenie)	$i 4 i 1 \ \4&16&24&16&4\\6&24&36&24&6\\4&16&24&16&4\\1&4&6&4&1\end{bmacierz}}}$
Maskowanie wyostrzające 5 × 5 Na podstawie rozmycia gaussowskiego o wartości równej 1 i wartości progowej równej 0 (bez maski obrazu )	${\ Displaystyle {\ Frac {-1} {256}} {\ rozpocząć {bmatrix }1&4&\ \ 6&4&1\\4&16&\ \ 24&16&4\\6&24&-476&24&6\\4&16&\ \ 24&16&4\\1&4&\ \ 6&4&1\end{bmacierz}}}$

Powyższe to tylko kilka przykładów efektów, które można osiągnąć poprzez splot jąder i obrazów.

Pochodzenie

Początek to pozycja jądra, która znajduje się powyżej (koncepcyjnie) bieżącego piksela wyjściowego. Może to być poza rzeczywistym jądrem, chociaż zwykle odpowiada jednemu z elementów jądra. W przypadku jądra symetrycznego początek jest zwykle elementem środkowym.

Skręt

Animacja splotu 2D

Konwolucja to proces dodawania każdego elementu obrazu do jego lokalnych sąsiadów, ważonych przez jądro. Jest to związane z pewną formą splotu matematycznego . Wykonywana operacja na macierzach — splot — nie jest tradycyjnym mnożeniem macierzy, mimo że jest podobnie oznaczona przez *.

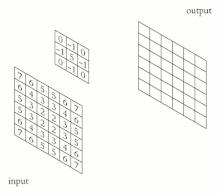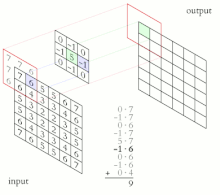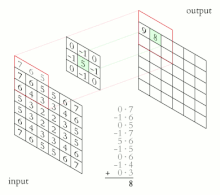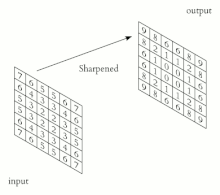
Na przykład, jeśli mamy dwie macierze trzy na trzy, pierwszą jądro, a drugą fragment obrazu, splot to proces odwracania zarówno wierszy, jak i kolumn jądra oraz mnożenia lokalnie podobnych wpisów i sumowania. Element o współrzędnych [2, 2] (czyli element środkowy) wynikowego obrazu byłby ważoną kombinacją wszystkich wpisów macierzy obrazu, z wagami podanymi przez jądro:

{\ Displaystyle \ lewo ({\ rozpocząć {bmatrix} a & b & c \\ d & e & f \\ g & h & i \ koniec {bmatrix}} * {\ rozpocząć {bmatrix} 1 i 2 i 3 \\ 4 i 5 i 6 \\ 7 i 8 i 9 \ koniec {bmatrix}} \ prawo) [2 ,2]=(i\cdot 1)+(h\cdot 2)+(g\cdot 3)+(f\cdot 4)+(e\cdot 5)+(d\cdot 6)+(c\cdot 7)+(b\ckropka 8)+(a\ckropka 9).}

Inne wpisy byłyby podobnie ważone, gdzie umieszczamy środek jądra na każdym z punktów granicznych obrazu i obliczamy sumę ważoną.

Wartości danego piksela w obrazie wyjściowym są obliczane przez pomnożenie każdej wartości jądra przez odpowiednie wartości pikseli obrazu wejściowego. Można to opisać algorytmicznie za pomocą następującego pseudokodu:

               
                     
                     dla każdego  wiersza obrazu  w  obrazie wejściowym  :  dla każdego  piksela  w  wierszu obrazu  :  ustaw  akumulator  na zero  dla każdego  wiersza jądra  w  jądrze  :  dla każdego  elementu  w  wierszu jądra  :  jeśli  pozycja elementu  odpowiada*  pozycji piksela ,   to  pomnóż  wartość elementu  odpowiadającą*  wartości piksela  dodać  
                

           wynik  do  akumulatora  endif  ustaw  piksel obrazu wyjściowego  na  akumulator

*odpowiadające pikselom obrazu wejściowego są znajdowane względem początku jądra.

Jeśli jądro jest symetryczne, umieść środek (początek) jądra na bieżącym pikselu. Jądro będzie nakładać się na sąsiednie piksele wokół początku. Każdy element jądra należy pomnożyć przez wartość piksela, z którym się pokrywa, a wszystkie otrzymane wartości zsumować. Ta wypadkowa suma będzie nową wartością dla bieżącego piksela, który obecnie pokrywa się ze środkiem jądra.

Jeśli jądro nie jest symetryczne, należy je odwrócić zarówno wokół osi poziomej, jak i pionowej przed obliczeniem splotu jak powyżej.

Ogólna postać splotu macierzy to

{\ Displaystyle {\ rozpocząć {bmatrix} x_ {11}& x_ {12} i \ cdots & x_ {1n} \\ x_ {21} & x_ {22} i \ cdots & x_ {2n} \\\ vdots & \ vdots & \ ddots &\vdots \\x_{m1}&x_{m2}&\cdots &x_{mn}\\\end{bmatrix}}*{\begin{bmatrix}y_{11}&y_{12}&\cdots &y_{1n }\\y_{21}&y_{22}&\cdots &y_{2n}\\\vdots &\vdots &\ddots &\vdots \\y_{m1}&y_{m2}&\cdots &y_{mn}\\ \end{bmatrix}}=\sum _{i=0}^{m-1}\sum _{j=0}^{n-1}x_{(mi)(nj)}y_{(1+i )(1+j)}}

Obsługa krawędzi

Rozszerz obsługę krawędzi

Splot jądra zwykle wymaga wartości z pikseli poza granicami obrazu. Istnieje wiele metod obsługi krawędzi obrazu.

Rozszerz: Najbliższe piksele graniczne są koncepcyjnie rozszerzane na tyle, na ile jest to konieczne, aby zapewnić wartości dla splotu. Piksele narożne są wydłużone w kliny o kącie 90°. Inne piksele krawędziowe są rozciągnięte w linie.
Zawijanie: Obraz jest koncepcyjnie zawijany (lub kafelkowany), a wartości są pobierane z przeciwległej krawędzi lub rogu.
Lustro: Obraz jest koncepcyjnie lustrzanym odbiciem na krawędziach. Na przykład próba odczytania piksela 3 jednostki poza krawędzią powoduje zamiast tego odczytanie jednej 3 jednostek wewnątrz krawędzi.
Przytnij / Unikaj nakładania się: Każdy piksel w obrazie wyjściowym, który wymagałby wartości spoza krawędzi, jest pomijany. Ta metoda może spowodować, że obraz wyjściowy będzie nieco mniejszy, a krawędzie zostaną przycięte. Przenieś jądro, aby wartości spoza obrazu nigdy nie były wymagane. Uczenie maszynowe wykorzystuje głównie to podejście. Przykład: rozmiar jądra 10x10, rozmiar obrazu 32x32, wynikowy obraz to 23x23.
Przycinanie jądra: Każdy piksel w jądrze, który wykracza poza obraz wejściowy, nie jest używany, a normalizacja jest dostosowywana w celu kompensacji.
Stała: Użyj stałej wartości dla pikseli poza obrazem. Zwykle używany jest kolor czarny lub czasami szary. Ogólnie zależy to od zastosowania.

Normalizacja

Normalizację definiuje się jako dzielenie każdego elementu w jądrze przez sumę wszystkich elementów jądra, tak aby suma elementów znormalizowanego jądra była jednością. Dzięki temu średni piksel w zmodyfikowanym obrazie będzie tak jasny, jak przeciętny piksel w oryginalnym obrazie.

Optymalizacja

Algorytmy szybkiego splotu obejmują:

splot rozdzielny

Rozdzielny splot

Splot 2D z jądrem M × N wymaga mnożenia M × N dla każdej próbki (piksel). Jeśli jądro jest rozdzielne, obliczenia można zredukować do mnożenia M + N. Używanie splotów rozdzielnych może znacznie zmniejszyć obliczenia, wykonując dwa sploty 1D zamiast jednego splotu 2D.

Realizacja

Tutaj konkretna implementacja splotu wykonana za pomocą języka cieniowania GLSL :













 // autor : csblo  // Praca wykonana tylko przez konsultację :  // https://en.wikipedia.org/wiki/Kernel_(image_processing)  // Zdefiniuj jądra  #define identity mat3(0, 0, 0, 0, 1, 0, 0, 0, 0)  #define edge0 mat3(1, 0, -1, 0, 0, 0, -1, 0, 1)  #define edge1 mat3(0, 1, 0, 1, -4, 1 , 0, 1, 0)  #define edge2 mat3(-1, -1, -1, -1, 8, -1, -1, -1, -1)  #define wyostrz mat3(0, -1, 0, -1, 5, -1, 0, -1, 0)  #define box_blur mat3(1, 1, 1, 1, 1, 1, 1, 1, 1) * 0.1111  #define gaussian_blur mat3(1, 2, 1 , 2, 4, 2, 1, 2, 1) * 0.0625  #define emboss mat3(-2, -1, 0, -1, 1, 1, 0, 1, 2) 


  

      
          0   
         0 0 0  // Znajdź współrzędne elementu macierzy z indeksu  vec2  kpos  (  int  index  )  {  return  vec2  [  9  ]  (  vec2  (  -  1  ,  -  1  ),  vec2  (  ,  -  1  ),  vec2  (  1  ,  -  1  ),  vec2  (  -  1  ,  ),  vec2  (  ,  ),  vec2  (  0 
          0   
      







 1  ,  ),  vec2  (  -  1  ,  1  ),  vec2  (  ,  1  ),  vec2  (  1  ,  1  )  ) [  indeks  ]  /  iRozdzielczość  .  xy  ;  [  _  _  _  _  _  _     

    
     
    
        0    
              3  ]  region3x3  (  sampler2D  sampler  ,  vec2  uv  )  {  // Utwórz każdy piksel dla regionu  vec4  [  9  ]  region  ;  for  (  int  i  =  ;  i  <  9  ;  i  ++  )  region  [  i  ]  =  tekstura  (  sampler  ,  uv  +  kpos  (  i  )); 

    
     
    
        0    
          
        	0  
        	 // Utwórz region 3x3 z 3 kanałami kolorów (czerwony, zielony, niebieski)  mat3  [  3  ]  mRegion  ;  for  (  int  i  =  ;  i  <  3  ;  i  ++  )  mRegion  [  i  ]  =  mat3  (  region  [  ][  i  ],  region  [  1  ][  i  ],  region  [  2  ][  i  ],  region   
        	  
    	
    
     



 [  3  ][  ja  ],  region  [  4  ][  ja  ],  region  [  5  ][  ja  ],  region  [  6  ][  ja  ],  region  [  7  ][  ja  ],  region  [  8  ][  ja  ]  );  zwróć  mRegion  ;  }  // Konwolucja tekstury za pomocą jądra  // kernel : jądro używane do konwolucji 


      

     
    
    
        
    
    
        // sampler: sampler tekstury  // uv: aktualne współrzędne samplera  splot  vec3  (  jądro  mat3  ,  sampler2D  sampler  ,  vec2  uv  )  {  fragment  vec3  ;  // Wyodrębnij region 3x3 wyśrodkowany w uv  mat3  [  3  ]  region  =  region3x3  (  sampler  ,  uv  );  // dla każdego kanału koloru regionu  for  (  int  i  =  0    
    
        
           
        
            
        
           00  0  ;  ja  <  3  ;  i  ++  )  {  // pobierz kanał regionu  mat3  rc  =  region  [  i  ];  // komponentowe mnożenie jądra przez region kanał  mat3  c  =  matrixCompMult  (  kernel  ,  rc  );  // dodaj każdy składnik macierzy  float  r  =  c  [  ][  ]  +  c  [  1  ][  ]  +  0
                 0    
                 0    
        
        
         do  [  2  ][  ]  +  do  [  ][  1  ]  +  do  [  1  ][  1  ]  +  do  [  2  ][  1  ]  +  do  [  ][  2  ]  +  do  [  1  ][  2  ]  +  do  [  2  ][  2  ];  // dla fragmentu na kanale i ustaw wynikowy  fragment  [  i   
    
    
         


        

    
       
    
         ]  =  r  ;  }  zwróć  fragment  ;  }  void  mainImage  (  out  vec4  fragColor  ,  in  vec2  fragCoord  )  {  // Znormalizowane współrzędne piksela (od 0 do 1)  vec2  uv  =  fragCoord  /  iResolution  .  xy  ;  // Jądro Convolve z teksturą  vec3  col  =  convolution  (  emboss  ,  iChannel0  
    
    
       
 ,  uv  );  // Wyjście na ekran  fragColor  =  vec4  (  col  ,  1.0  );  }

Ludwig, Jamie (nd). Splot obrazu (PDF) . Uniwersytet Stanowy w Portland .
Lecarme, Olivier; Delvare, Karine (styczeń 2013). Księga GIMP: kompletny przewodnik po prawie wszystkim . Prasa bez skrobi . P. 429. ISBN 978-1593273835 .
Gumster, Jason van; Szymonski, Robert (marzec 2012). Biblia GIMP-a . Wiley'a _ s. 438–442. ISBN 978-0470523971 .
Shapiro, Linda G .; Stockman, George C. (luty 2001). Wizja komputerowa . Sala Prentice'a . s. 53–54. ISBN 978-0130307965 .

Zobacz też

Linki zewnętrzne