Wielowymiarowy splot dyskretny

W przetwarzaniu sygnałów wielowymiarowy splot dyskretny odnosi się do operacji matematycznej między dwiema funkcjami f i g na n -wymiarowej siatce, która tworzy trzecią funkcję, również n -wymiarową. Wielowymiarowy splot dyskretny jest dyskretnym analogiem wielowymiarowego splotu funkcji w przestrzeni euklidesowej. Jest to również szczególny przypadek splotu na grupach , gdy grupa jest grupą n -krotek liczb całkowitych.

Definicja

Opis problemu i podstawy

Podobnie jak w przypadku jednowymiarowym, gwiazdka jest używana do reprezentowania operacji splotu. Liczba wymiarów w danej operacji jest odzwierciedlona w liczbie gwiazdek. Na przykład M -wymiarowy zostałby zapisany za pomocą głównych gwiazdek. Poniżej przedstawiono M -wymiarowy splot sygnałów dyskretnych:

${\ Displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}, n_ {2}, ..., n_ {M}) * {\ overset {M}{\cdots}}*h(n_{1},n_{2},...,n_{M})}$

W przypadku sygnałów o wartościach dyskretnych ten splot można obliczyć bezpośrednio w następujący sposób:

${\ Displaystyle \ suma _ {k_ {1} = - \ infty} ^ {\ infty} \ suma _ {k_ {2} = - \ infty} ^ {\ infty} ...$

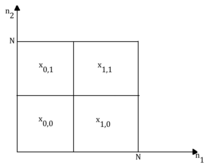
Otrzymany wyjściowy obszar wsparcia dyskretnego splotu wielowymiarowego zostanie określony na podstawie rozmiaru i obszarów wsparcia dwóch sygnałów wejściowych.

Wizualizacja splotu między dwoma prostymi sygnałami dwuwymiarowymi

Wymieniono kilka właściwości dwuwymiarowego operatora splotu. Należy zauważyć, że można je również rozszerzyć na sygnały o ${\ displaystyle N}$ .

Właściwość przemienna:

${\ Displaystyle x ** h = h ** x}$

Własność powiązana:

${\ Displaystyle (x ** h) ** g = x ** (h ** g)}$

Własność rozdzielcza:

${\ Displaystyle x ** (h + g) = (x ** h) + (x ** g)}$

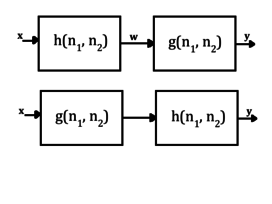
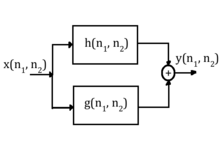
Te właściwości są widoczne w użyciu na poniższym rysunku. Biorąc pod $Displaystyle h$ pewne dane wejściowe ${$ filtra z odpowiedzią impulsową, , a następnie kolejny filtr z odpowiedzią impulsową ${\ Displaystyle g (n_ {1}, n_ {2})}$ , wynik jest określony przez ${\ Displaystyle y (n_ {1}, n_ {2})}$ . Załóżmy, że dane wyjściowe pierwszego filtra są określone przez ${\ Displaystyle w (n_ {1}, n_ {2})}$ , oznacza to, że:

${\ Displaystyle w = x ** h}$

Ponadto ta funkcja pośrednia jest następnie spleciona z odpowiedzią impulsową drugiego filtra, a zatem wynik może być reprezentowany przez:

${\ Displaystyle y = w ** g = (x ** h) ** g}$

Korzystając z właściwości asocjacyjnej, można to przepisać w następujący sposób:

${\ Displaystyle y = x ** (h ** g)}$

co oznacza, że ​​równoważna odpowiedź impulsowa dla systemu kaskadowego jest dana przez:

${\ Displaystyle h_ {równ.} = h ** g}$

Obie figury przedstawiają systemy kaskadowe. Należy zauważyć, że kolejność filtrów nie wpływa na dane wyjściowe.

Podobną analizę można przeprowadzić na zbiorze systemów równoległych przedstawionych poniżej.

Układ z zestawem filtrów równoległych.

W tym przypadku jasne jest, że:

${\ Displaystyle y = (x ** h) + (x ** g)}$

Wykorzystując prawo rozdzielności wykazano, że:

${\ Displaystyle y = x ** (h + g)}$

Oznacza to, że w przypadku układu równoległego równoważną odpowiedź impulsową zapewniają:

${\ Displaystyle h_ {równ.} = h + g}$

$w$ systemach kaskadowych, jak i systemach równoległych można uogólnić na systemy z -liczbą filtrów.

Motywacja i zastosowania

Splot w jednym wymiarze był potężnym odkryciem, które umożliwiło łatwe porównanie danych wejściowych i wyjściowych liniowego systemu niezmiennego z przesunięciem (LSI) (patrz teoria systemu LTI ), o ile znana była odpowiedź impulsowa systemu filtrów. Pojęcie to przenosi się również do wielowymiarowego splotu, ponieważ sama znajomość odpowiedzi impulsowej filtra wielowymiarowego również pozwala na bezpośrednie porównanie wejścia i wyjścia systemu. Jest to ważne, ponieważ kilka sygnałów przesyłanych dziś w cyfrowym świecie ma wiele wymiarów, w tym obrazy i filmy. Podobnie jak splot jednowymiarowy, splot wielowymiarowy umożliwia obliczenie wyjścia systemu LSI dla danego sygnału wejściowego.

Rozważmy na przykład obraz przesyłany przez sieć bezprzewodową, na którą narażony jest szum elektrooptyczny. Możliwe źródła zakłóceń obejmują błędy w transmisji kanału, przetwornik analogowo-cyfrowy i czujnik obrazu. Zwykle szum powodowany przez kanał lub czujnik tworzy niezależne przestrzennie składowe sygnału o wysokiej częstotliwości, które przekładają się na dowolne jasne i ciemne plamy na rzeczywistym obrazie. Aby pozbyć się danych obrazu z zawartości widmowej o wysokiej częstotliwości, można ją pomnożyć przez odpowiedź częstotliwościową filtra dolnoprzepustowego, co w oparciu o twierdzenie o splotach jest równoważne splataniu sygnału w domenie czasowo-przestrzennej przez odpowiedź impulsowa filtra dolnoprzepustowego. Kilka odpowiedzi impulsowych, które to robią, pokazano poniżej.

Odpowiedzi impulsowe typowych wielowymiarowych filtrów dolnoprzepustowych

Oprócz filtrowania zawartości widmowej, splot wielowymiarowy może implementować wykrywanie krawędzi i wygładzanie. To znowu jest całkowicie zależne od wartości odpowiedzi impulsowej, która jest używana do splotu z obrazem wejściowym. Typowe odpowiedzi impulsowe dla wykrywania krawędzi przedstawiono poniżej.

Typowe odpowiedzi impulsowe dla wykrywania krawędzi

Oryginalny obraz (po lewej) i obraz po przejściu przez filtr wykrywający krawędzie (po prawej)

Oprócz przetwarzania obrazu można zaimplementować splot wielowymiarowy, aby umożliwić wiele innych zastosowań. Ponieważ filtry są szeroko rozpowszechnione w cyfrowych systemach komunikacyjnych, każdy system, który musi przesyłać wielowymiarowe dane, jest wspomagany technikami filtrowania. Jest on używany w przetwarzaniu wideo w czasie rzeczywistym, analizie sieci neuronowych, cyfrowej analizie danych geofizycznych i wielu innych.

Jednym z typowych zniekształceń występujących podczas przechwytywania lub przesyłania obrazów i wideo jest rozmycie spowodowane procesem filtrowania dolnoprzepustowego. Wprowadzone rozmycie można modelować za pomocą gaussowskiego filtrowania dolnoprzepustowego.

Obraz oryginalny (po lewej) i obraz rozmyty (po prawej) wykonane przy użyciu splotu Gaussa

Dekompozycja wiersz-kolumna z sygnałami rozdzielnymi

Sygnały rozdzielne

O sygnale mówi się, że jest separowalny , jeśli można go zapisać jako iloczyn wielu jednowymiarowych sygnałów. Matematycznie wyraża się to następująco:

${\ Displaystyle x (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}) x (n_ {2}) ... x (n_ {M})}$

Niektóre łatwo rozpoznawalne sygnały, które można rozdzielić, obejmują funkcję skoku jednostkowego i funkcję impulsu diraca-delta.

${\ Displaystyle u (n_ {1}, n_ {2}, ..., n_ {M}) = u (n_ {1}) u (n_ {2}) ... u (n_ {M})}$ (funkcja kroku jednostkowego)

${\ Displaystyle \ delta (n_ {1}, n_ {2}, ..., n_ {M}) = \ delta (n_ {1}) \ delta (n_ {2}) ... \delta (n_{M})}$ (funkcja impulsowa dirac-delta)

Splot jest operacją liniową. Wynika z tego, że wielowymiarowy splot sygnałów rozdzielnych można wyrazić jako iloczyn wielu splotów jednowymiarowych. Rozważmy na przykład przypadek, w którym x i h są funkcjami rozdzielnymi.

${\ Displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = \ suma _ {k_ {1} = - \ infty} ^ {\ infty} \sum _{k_{2}=-\infty }^{\infty }h(k_{1},k_{2})x(n_{1}-k_{1},n_{2}-k_{2 })}$

Stosując właściwości rozdzielności, można to następnie przepisać w następujący sposób:

${\ Displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = {\ bigg (} \ suma _ {k_ {1}=-\infty }^{\infty }h(k_{1})x(n_{1}-k_{1}){\bigg )}{\bigg (}\suma _{k_{2} =-\infty}^{\infty}h(k_{2})x(n_{2}-k_{2}){\bigg )}}$

Łatwo więc zauważyć, że sprowadza się to do iloczynu jednowymiarowych splotów:

${\ Displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = {\ bigg [} x (n_ {1}) * h (n_ {1}) {\bigg ]}{\bigg [}x(n_{2})*h(n_{2}){\bigg]}}$

Wniosek ten można następnie rozszerzyć na splot dwóch rozdzielnych sygnałów M -wymiarowych w następujący sposób:

${\ Displaystyle x (n_ {1}, n_ {2}, ..., n_ {M}) * {\ overset {M} {\ cdots}} * h(n_{1},n_{2},...,n_{M})={\bigg [}x(n_{1})*h(n_{1}){\bigg ]}{\bigg [}x(n_{2})*h(n_{2}){\bigg ]}...{\bigg [}x(n_{M})*h(n_{M}){\bigg ]} }$

$są rozdzielne,$ można obliczyć, obliczając sploty jednowymiarowe.

Dekompozycja wiersz-kolumna

Metodę wiersz-kolumna można zastosować, gdy jeden z sygnałów w splocie jest rozdzielny. Metoda wykorzystuje właściwości separowalności w celu uzyskania metody obliczania splotu dwóch wielowymiarowych sygnałów, która jest bardziej wydajna obliczeniowo niż bezpośrednie obliczanie każdej próbki (biorąc pod uwagę, że jeden z sygnałów jest separowalny). $)$ matematyczne rozumowanie stojące za podejściem dekompozycji wierszy rozdzielnym

${\ Displaystyle {\ rozpocząć {wyrównane} y (n_ {1}, n_ {2}) & = \ suma _ {k_ {1} = - \ infty} ^ {\ infty} \ suma _ {k_ {2} = -\infty }^{\infty}h(k_{1},k_{2})x(n_{1}-k_{1},n_{2}-k_{2})\\&=\suma _ {k_{1}=-\infty}^{\infty}\sum _{k_{2}=-\infty}^{\infty}h_{1}(k_{1})h_{2}(k_{ 2})x(n_{1}-k_{1},n_{2}-k_{2})\\&=\suma _{k_{1}=-\infty }^{\infty }h_{1 }(k_{1}){\Bigg [}\suma _{k_{2}=-\infty }^{\infty }h_{2}(k_{2})x(n_{1}-k_{1 },n_{2}-k_{2}){\Bigg ]}\end{wyrównane}}}$

$- \ infty} ^ {\ infty } h_ {2} (k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2})}$ = może być teraz ponownie użyte podczas oceny innych wartości ${\ displaystyle y}$ o wspólnej wartości ${\ displaystyle n_ {2}}$ :

${\ Displaystyle {\ rozpocząć {wyrównane} y (n_ {1} + \ delta, n_ {2}) & = \ suma _ {k_ {1} = - \ infty} ^ {\ infty} h_ {1} (k_ {1}){\Bigg [}\suma _{k_{2}=-\infty}^{\infty}h_{2}(k_{2})x(n_{1}-[k_{1}- \delta ],n_{2}-k_{2}){\Bigg ]}\\&=\sum _{k_{1}=-\infty }^{\infty }h_{1}(k_{1} +\delta ){\Bigg [}\suma _{k_{2}=-\infty }^{\infty }h_{2}(k_{2})x(n_{1}-k_{1},n_ {2}-k_{2}){\Bigg ]}\end{wyrównane}}}$

$skutecznie$ operację splotu na wszystkich wierszach wszystkich swoich kolumn. Podejście to można dodatkowo zoptymalizować, biorąc pod uwagę sposób dostępu do pamięci w procesorze komputera.

Procesor załaduje dane sygnałowe potrzebne do wykonania danej operacji. W przypadku nowoczesnych procesorów dane będą ładowane z pamięci do pamięci podręcznej procesora, która ma krótszy czas dostępu niż pamięć. Sama pamięć podręczna jest podzielona na wiersze. Gdy wiersz pamięci podręcznej jest ładowany z pamięci, jednocześnie ładowanych jest wiele operandów danych. Rozważmy zoptymalizowany przypadek, w którym wiersz danych sygnału może w całości zmieścić się w pamięci podręcznej procesora. Ten konkretny procesor byłby w stanie wydajnie uzyskiwać dostęp do danych w wierszach, ale nie w kolumnach, ponieważ różne operandy danych w tej samej kolumnie leżałyby w różnych wierszach pamięci podręcznej. Aby skorzystać ze sposobu, w jaki uzyskuje się dostęp do pamięci, bardziej wydajna jest transpozycja zestawu danych, a następnie osiowanie go według wierszy, niż próba uzyskania dostępu do niego według kolumn. Algorytm staje się wtedy:

1. $h_ {1} (n_ {1})}$$rozdzielenia$ dwuwymiarowy sygnał dwa jednowymiarowe sygnały i ${\ Displaystyle h_ {2} (n_ {2})}$
2. Wykonaj splot w rzędach na poziomych składowych sygnału ${\ Displaystyle x (n_ {1}, n_ {2})}$ używając ${\ Displaystyle h_ {1} (n_ {1})}$ , aby uzyskać ${\ Displaystyle g (n_ {1}, n_ {2})}$
3. Transponuj pionowe składowe sygnału wynikające z kroku 2. ${\ Displaystyle g (n_ {1}, n_ {2})}$
4. Wykonaj splot w wierszach na transponowanych pionowych składowych ${\ Displaystyle g (n_ {1}, n_ {2})}$ , aby uzyskać żądany wynik ${\ styl wyświetlania y(n_{1},n_{2})}$

Przyspieszenie obliczeniowe z dekompozycji wiersz-kolumna

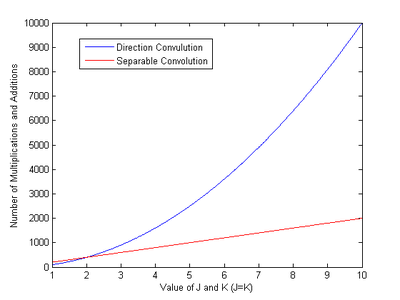
$w$$,$ obraz o rozmiarze jest separowalny filtr o Sam obraz jest nierozdzielny. Jeśli wynik zostanie obliczony przy użyciu metody bezpośredniego splotu bez wykorzystywania możliwości rozdzielenia filtra, będzie to wymagało około ${\ displaystyle XYJK}$ mnożenia i dodawania. Jeśli weźmie się pod uwagę możliwość rozdzielenia filtra, filtrowanie można przeprowadzić w dwóch etapach. Pierwszy krok będzie miał $displaystyle XYJ + XYK}$ , a drugi krok będzie miał ${\ Displaystyle$$XYK}$ , co daje w sumie lub ${\ Displaystyle XY (J + K)}$ mnożenia i dodawania. Porównanie złożoności obliczeniowej splotu bezpośredniego i rozdzielnego przedstawiono na poniższym obrazku:

Liczba obliczeń przechodzących przez obraz 10 x 10 przez filtr o rozmiarze J x K , gdzie J = K zmienia się w zakresie od 1 do 10

Splot kołowy sygnałów wielowymiarowych o wartościach dyskretnych

Założeniem podejścia do splotu kołowego w przypadku sygnałów wielowymiarowych jest opracowanie związku między twierdzeniem o splotach a dyskretną transformatą Fouriera (DFT), który można wykorzystać do obliczenia splotu między dwoma sygnałami o skończonych rozmiarach i wartościach dyskretnych.

Twierdzenie o splotach w wielu wymiarach

W przypadku sygnałów jednowymiarowych twierdzenie o splocie stwierdza, że ​​transformata Fouriera splotu między dwoma sygnałami jest równa iloczynowi transformat Fouriera tych dwóch sygnałów. Zatem splot w dziedzinie czasu jest równy mnożeniu w dziedzinie częstotliwości. Matematycznie zasada ta jest wyrażona przez:

$${\ Displaystyle y (n) = h (n) * x (n) \ longleftrightarrow Y (\ omega )=H(\omega)X(\omega)}$$

Tę zasadę można bezpośrednio rozszerzyć na radzenie sobie z sygnałami o wielu wymiarach.

$${\ Displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = h (n_ {1}, n_ {2}, ..., n_ {M}) * {\ overset {M}{\cdots}}*x(n_{1},n_{2},...,n_{M})\longleftrightarrow Y(\omega _{1},\omega _{2},.. .,\omega _{M})=H(\omega _{1},\omega _{2},...,\omega _{M})X(\omega _{1},\omega _{ 2},...,\omega _{M})}$$

Właściwość tę można łatwo rozszerzyć na użycie z dyskretną transformatą Fouriera (DFT) w następujący sposób (należy zauważyć, że splot liniowy jest zastępowany splotem kołowym, gdzie jest używany do oznaczenia operacji splotu kołowego o rozmiarze $N}$$\ otimes}$$displaystyle$ ):

${\ Displaystyle y (n) = h (n) \ czasami x (n) \ longleftrightarrow Y ( k)=H(k)X(k)}$

W przypadku sygnałów o wielu wymiarach:

$${\ Displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = h (n_ {1}, n_ {2}, ..., n_ {M}) \ czasami {\ overset {M}{\cdots }}\czasami x(n_{1},n_{2},...,n_{M})\longleftrightarrow Y(k_{1},k_{2},..., k_{M})=H(k_{1},k_{2},...,k_{M})X(k_{1},k_{2},...,k_{M})}$$

Okrągłe sploty tutaj będą miały rozmiar $, N_ {M}}$ .

Podejście do splotu kołowego

Motywacją do zastosowania metody splotu kołowego jest to, że opiera się ona na DFT. Założeniem splotu kołowego jest pobranie DFT sygnałów wejściowych, pomnożenie ich razem, a następnie wzięcie odwrotnej DFT. Należy uważać, aby użyto wystarczająco dużej DFT, aby nie wystąpiło aliasing. DFT jest obliczalny numerycznie, gdy mamy do czynienia z sygnałami o skończonym zasięgu. Jedną z zalet tego podejścia jest to, że ponieważ wymaga zastosowania DFT i odwrotnej DFT, możliwe jest wykorzystanie wydajnych algorytmów, takich jak szybka transformata Fouriera (FFT). Splot kołowy można również obliczyć w dziedzinie czasu/przestrzeni, a nie tylko w dziedzinie częstotliwości.

Schemat blokowy splotu kołowego z sygnałami 2 M -wymiarowymi

Wybór rozmiaru DFT, aby uniknąć aliasingu

Rozważmy następujący przypadek, w którym brane są dwa sygnały x i h o skończonym zasięgu. Dla obu sygnałów istnieje odpowiednia DFT w następujący sposób:

$_$ _ ${\ Displaystyle h (n_ {1}, n_ {2}) \ longleftrightarrow H (k_ {1}, k_ {2})}$

Region wsparcia wynosi ${\ Displaystyle x (n_ {1}, n_ {2})}$ jest ${\ Displaystyle 0 \ równoważnik n_ {1} \ równoważnik P_ {1} -1}$ i ${\ Displaystyle 0 \ równoważnik n_ {2} \ równoważnik P_ {2} -1}$ i region wsparcia ${\ Displaystyle h (n_ {1}, n_ {2})}$ jest ${\ Displaystyle 0 \ równoważnik n_ {1} \ równoważnik Q_ {1} -1}$ i ${\ Displaystyle 0 \ równoważnik n_ {2} \ równoważnik Q_ {2} -1}$ .

Splot liniowy tych dwóch sygnałów byłby przedstawiony jako:

$${\ Displaystyle y_ {liniowy} (n_{1},n_{2})=\suma_{m_{1}}\suma_{m_{2}}h(m_{1},m_{2})x(n_{1}-m_ {1},n_{2}-m_{2})}$$

${1},$ regiony wsparcia i ( $h$ , region wsparcia ${\ Displaystyle y_ {liniowy} (n_ {1}, n_ {2})}$ zostanie podany jako następny:

$${\ Displaystyle 0 \ równoważnik n_ {1} \ równoważnik P_ {1} + Q_ {1} -1}$$

$${\ Displaystyle 0 \ równoważnik n_ {2} \ równoważnik P_ {2} + Q_ {2} -1}$$

$\ Displaystyle N_ {1} \ geq \ max (P_ {1}, Q_ {1})}$ zastosować DFT o rozmiarze $N$$Displaystyle N_$ i ${\ Displaystyle N_ {2} \ geq \ max (P_ {2} ,Q_{2})}$ ponieważ ten sam rozmiar DFT musi być użyty w obu sygnałach. W przypadku, gdy potrzebny jest rozmiar DFT większy niż zasięg sygnału, sygnał jest wypełniany zerami, aż osiągnie wymaganą długość. Po pomnożeniu DFT i odwróceniu DFT do wyniku, wynikowy splot kołowy jest następnie określony wzorem:

${\ Displaystyle y_ {okrągły} (n_ {1}, n_ {2}) = \ suma _ {r_ {1}} \ suma _{r_{2}}{\Bigg [}\suma _{m_{1}=0}^{Q_{1}-1}\suma _{m_{2}=0}^{Q_{2}- 1}h(m_{1},m_{2})x(n_{1}-m_{1}-r_{1}N_{1},n_{2}-m_{2}-r_{2}N_ {2}){\Bigg ]}}$ dla ${\ Displaystyle (n_ {1}, n_ {2}) \ w R_ {N_ {1} N_ {2}}}$

${\ Displaystyle R_ {N_ {1} N_ {2}} \ trójkątq \ {(n_{1},n_{2}):0\równoważnik n_{1}\równoważnik N_{1}-1,0\równoważnik n_{2}\równoważnik N_{2}-1\}}$

Rezultat będzie taki, że y $\ Displaystyle y_ {okrągły} (n_ {1}, n_ {2})}$ wynik $\ Displaystyle y_ {liniowy} (n_ {1}, n_ {2})}$ . Można to wyrazić następująco:

${\ Displaystyle y_ {kolisty} (n_ {1}, n_ {2}) = \ suma _ {r_ {1}} \ suma _ {r_ {2}} y_ {liniowy }(n_{1}-r_{1}N_{1},n_{2}-r_{2}N_{2}){\mathrm {\,\,\,dla\,\,\,} }( n_{1},n_{2})\w R_{N_{1}N_{2}}}$

Następnie, aby uniknąć aliasingu między replikami z aliasami przestrzennymi, należy wybrać i $displaystyle N_ {2}},$${\$ aby spełniały następujące warunki:

${\ Displaystyle N_ {1} \ geq P_ {1} + Q_ {1} -1}$

${\ Displaystyle N_ {2} \ geq P_ {2} + Q_ {2} -1}$

Jeśli te warunki są spełnione, to wyniki splotu kołowego będą równe wynikom splotu liniowego (biorąc główny okres splotu kołowego jako obszar podparcia). To jest:

${\ Displaystyle y_ {okrągły} (n_ {1}, n_ {2}) = y_{liniowy}(n_{1},n_{2})}$ dla ${\ Displaystyle (n_ {1}, n_ {2}) \ w R_ {N_ {1} N_ {2}}}$

Podsumowanie procedury z wykorzystaniem DFT

Twierdzenie o splocie i splot kołowy można zatem wykorzystać w następujący sposób, aby uzyskać wynik równy wykonaniu splotu liniowego:

1. Wybierz ${\ Displaystyle N_ {1}}$ i ${\ Displaystyle N_ {2}}$ , aby zaspokoić ${\ Displaystyle N_ {1} \ geq P_ {1} + Q_ { 1} -1}$ i ${\ Displaystyle N_ {2} \ geq P_ {2} + Q_ {2} -1}$
2. $n_ {1}$ sygnałów $\$ Displaystyle tak, że oba mają rozmiar ${\ Displaystyle N_ {1} \ razy N_ {2}}$
3. Oblicz DFT zarówno ${\ Displaystyle h (n_ {1}, n_ {2})}$ i ${\ Displaystyle x (n_ {1}, n_ { 2})}$
4. Pomnóż wyniki DFT, aby uzyskać ${\ Displaystyle Y (k_ {1}, k_ {2}) = H (k_{1},k_{2})X(k_{1},k_{2})}$
5. Wynik IDFT z ${\ Displaystyle Y (k_ {1}, k_ {2})}$ będzie wtedy równy wynikowi wykonania splotu liniowego na dwóch sygnałach

Nałóż na siebie i dodaj

Inną metodą wykonywania splotów wielowymiarowych jest podejście polegające na nakładaniu i dodawaniu . Ta metoda pomaga zmniejszyć złożoność obliczeniową często związaną z wielowymiarowymi splotami ze względu na ogromne ilości danych nieodłącznie związanych z nowoczesnymi systemami cyfrowymi. Ze względu na zwięzłość jako przykładu użyto przypadku dwuwymiarowego, ale te same koncepcje można rozszerzyć na wiele wymiarów.

Rozważmy splot dwuwymiarowy za pomocą obliczeń bezpośrednich:

${\ Displaystyle y (n_ {1}, n_ {2}) = \ suma _ {k_ {1} = - \ infty} ^ {\ infty} \ suma _ {k_ {2} = - \ infty} ^ {\ infty }x(n_{1}-k_{1},n_{2}-k_{2})h(k_{1},k_{2})}$

$,$ że sygnał wyjściowy ma niezerowych współczynników, a odpowiedź impulsowa ma M niezerowych próbek i MN - 1 dodaje w celu obliczenia. Używając zamiast tego FFT, odpowiedź częstotliwościowa filtra i transformata Fouriera wejścia musiałaby być przechowywana w pamięci. Ogromne ilości obliczeń i nadmierne wykorzystanie przestrzeni pamięci stanowią problem, ponieważ dodaje się więcej wymiarów. W tym miejscu pojawia się metoda nakładania i dodawania splotów.

Dekompozycja na mniejsze bloki splotu

$,$ informacje $skutkuje$ podzielić na mniejsze bloki o wymiarach, co mniejszymi mniejsza złożoność obliczeniowa i mniejsze zapotrzebowanie na pamięć. Można to wyrazić matematycznie w następujący sposób:

${\ Displaystyle x (n_ {1}, n_ {2}) = \ suma _ {i=1}^{P_{1}}\suma _{j=1}^{P_{2}}x_{ij}(n_{1},n_{2})}$

gdzie ${\ Displaystyle x (n_ {1}, n_ {2})}$ reprezentuje sygnał wejściowy ${\ Displaystyle N_ {1}}$ x ${\ Displaystyle N_ {2}}$$P_ {1} P_ {2}}$ Displaystyle segmentów blokowych, z ${\ Displaystyle P_ {1} = N_ {1} / L_ {1 }}$ i ${\ Displaystyle P_ {2} = N_ {2} / L_ {2}}$ .

Aby wytworzyć sygnał wyjściowy, wykonywany jest splot dwuwymiarowy:

${\ Displaystyle y (n_ {1}, n_ {2}) = x (n_ {1}, n_{2})**h(n_{1},n_{2})}$

Podstawienie za ${\ Displaystyle x (n_ {1}, n_ {2})}$ skutkuje:

${\ Displaystyle y (n_ {1} ,n_{2})=\suma _{i=1}^{P_{1}}\suma _{j=1}^{P_{2}}x_{ij}(n_{1},n_{2 })**h(n_{1},n_{2})}$

Ten splot zwiększa złożoność niż splot bezpośredni; jednakże, ponieważ jest zintegrowany z szybkim splotem FFT, metoda nakładania się-dodawania działa szybciej i jest metodą bardziej wydajną pod względem pamięci, dzięki czemu jest praktyczna w przypadku dużych zestawów danych wielowymiarowych.

Podział procedury

Niech ${\ Displaystyle h (n_ {1}, n_ {2})}$ będzie miał rozmiar ${\ Displaystyle M_ {1} \ razy M_ {2}}$ :

1. Podziel wejście $2$$}}$ się bloki wymiarów $razy$ .
2. Zero pad ${\ Displaystyle h (n_ {1}, n_ {2})}$ tak, że ma wymiary ( ${\ Displaystyle L_ {1} + M_ {1} } -1}$ ) ${\ Displaystyle \ razy}$ ( ${\ Displaystyle L_ {2} + M_ {2} -1}$ ).
3. Użyj DFT, aby uzyskać ${\ Displaystyle H (k_ {1}, k_ {2})}$ .
4. Dla każdego bloku wejściowego:
   1. ${\ Displaystyle x_ {ij} (n_ {1}, n_ {2})}$ jot wymiary ( ${\ Displaystyle L_ {1} + M_ {1} -1}$ ) ${\ Displaystyle \ razy}$ ( ${\ Displaystyle L_ {2} + M_ {2} -1}$ ).
   2. Weź dyskretną transformatę Fouriera każdego bloku, aby dać ${\ Displaystyle X_ {ij} (k_ {1}, k_ {2})}$ .
   3. $(k_ {1}, k_ {2}) =X_{ij}(k_{1},k_{2})H(k_{1},k_{2})}$ jot .
   4. Weź odwrotną dyskretną transformatę Fouriera ${\ Displaystyle Y_ {ij} (k_ {1}, k_ {2})}$ , aby uzyskać ${\ Displaystyle y_{ij}(n_{1},n_{2})}$ .
5. Znajdź ${\ Displaystyle y (n_ {1}, n_ {2})}$ przez nakładanie się i dodanie ostatniego ${\ Displaystyle (M_ {1} -1)}$${\ Displaystyle \ razy}$${\ Displaystyle (M_ {2} -1)}$ próbki ${\ Displaystyle y_ {ij} (n_ {1}, n_ {2})}$ z pierwszymi próbkami y ${\ Displaystyle y_ {i + 1, j + 1} (n_ {1}, n_ {2})},$$\ Displaystyle (M_ {1}-1)}$${\ Displaystyle \ razy}$${\ Displaystyle (M_ {2} -1)}$ aby uzyskać wynik.

Obrazkowy sposób działania

Aby lepiej zwizualizować metodę nakładania i dodawania, poniższe ilustracje przedstawiają graficzną analizę metody. Załóżmy $poziomym,$ że wejście ma kwadratowy obszar na poniższym rysunku. Następnie jest dzielony na cztery mniejsze segmenty w taki sposób, że teraz składa się z czterech mniejszych kwadratów. Każdy blok zagregowanego sygnału ma wymiary ${\ Displaystyle (N/2)}$ ${\ Displaystyle \ razy}$${\ Displaystyle (N/2)}$ .

Zdekomponowany sygnał wejściowy

Następnie każdy składnik jest spleciony z odpowiedzią impulsową filtra. Należy zauważyć, że można tutaj zwizualizować zaletę takiej implementacji, ponieważ każdy z tych splotów można zrównoleglić na komputerze, o ile komputer ma wystarczającą ilość pamięci i zasobów do jednoczesnego przechowywania i wykonywania obliczeń.

$wykres$ po lewej stronie przedstawia splot odpowiadający składowej wejściowej odpowiednią odpowiedzią impulsową $\ displaystyle h (n_{1},n_{2})}$ . Na prawo od tego wejście jest następnie splecione z odpowiedzią impulsową ${\ displaystyle x_ {1,0}}$${\ displaystyle h (n_ {1}, n_ {2})}$ .

Splot poszczególnych składowych z odpowiedzią impulsową

Splot każdego składnika z podświetlonymi nakładającymi się częściami

Ten sam proces jest wykonywany odpowiednio dla pozostałych dwóch danych wejściowych i są one gromadzone razem w celu utworzenia splotu. Jest to przedstawione po lewej stronie.

$) {\$$N$ odpowiedź impulsowa filtra region wsparcia w obu wymiarach. Oznacza to, że każdy splot splata sygnały o wymiarach ${\ Displaystyle (N/2)}$${\ Displaystyle \ razy}$${\ Displaystyle (N/8)}$ w obu ${1}$$}$ { \

${\ Displaystyle (N/2)}$${\ Displaystyle +}$${\ Displaystyle (N/8)}$${\ Displaystyle -}$${\ Displaystyle 1}$ = ${\ Displaystyle (5/8) N-1}$

w obu kierunkach. Jaśniejsza niebieska część koreluje z nakładaniem się dwóch sąsiednich zwojów, podczas gdy ciemniejsza niebieska część koreluje z nakładaniem się wszystkich czterech zwojów. Wszystkie te nakładające się części są dodawane razem oprócz zwojów w celu utworzenia połączonego splotu ${\ Displaystyle y (n_ {1}, n_ {2})}$ .

Nakładaj się i oszczędzaj

Metoda nakładania i zapisywania, podobnie jak metoda nakładania i dodawania, jest również używana do zmniejszenia złożoności obliczeniowej związanej ze splotami w czasie dyskretnym. Ta metoda, w połączeniu z FFT, pozwala na filtrowanie ogromnych ilości danych przez system cyfrowy, jednocześnie minimalizując niezbędną przestrzeń pamięci używaną do obliczeń na ogromnych tablicach danych.

Porównanie nakładania się i dodawania

Metoda nakładania i zapisywania jest bardzo podobna do metod nakładania i dodawania z kilkoma godnymi uwagi wyjątkami. Metoda nakładania i dodawania obejmuje splot liniowy sygnałów w czasie dyskretnym, podczas gdy metoda nakładania się i oszczędzania obejmuje zasadę splotu kołowego. Ponadto metoda nakładania i zapisywania wykorzystuje tylko jednorazowe wypełnienie zerowe odpowiedzi impulsowej, podczas gdy metoda nakładania i dodawania obejmuje wypełnienie zerowe dla każdego splotu na każdym składniku wejściowym. Zamiast używać dopełnienia zerowego, aby zapobiec aliasingowi w dziedzinie czasu, jak jego odpowiednik z dodawaniem nakładania się, zapisywanie nakładania po prostu odrzuca wszystkie punkty aliasingu i zapisuje poprzednie dane w jednym bloku, aby zostały skopiowane do splotu dla następnego bloku.

W jednym wymiarze różnice w wydajności i metrykach przechowywania między tymi dwiema metodami są minimalne. Jednak w przypadku wielowymiarowego splotu metoda nakładania się i oszczędzania jest preferowana w stosunku do metody nakładania się i dodawania pod względem szybkości i możliwości przechowywania. Podobnie jak w przypadku nakładania się i dodawania, procedura odwołuje się do przypadku dwuwymiarowego, ale można ją łatwo rozszerzyć na wszystkie procedury wielowymiarowe.

Podział procedury

Niech ${\ Displaystyle h (n_ {1}, n_ {2})}$ będzie miał rozmiar ${\ Displaystyle M_ {1} \ razy M_ {2}}$ :

1. Wstaw ${\ Displaystyle (M_ {1}-1)}$ kolumny i ${\ Displaystyle (M_ {2} -1)}$ rzędy zer na początku sygnału wejściowego ${\ Displaystyle x (n_ {1}, n_ {2})}$ w obu wymiarach.
2. Podziel odpowiedni sygnał na nakładające się segmenty wymiarów ( ${\ Displaystyle L_ {1} + M_ {1} -1}$ ) ${\ Displaystyle \ razy}$ ( ${\ displaystyle L_ {2} + M_ {2} -1}$ ), w którym każdy dwuwymiarowy blok będzie się nakładać przez ${\ Displaystyle (M_ {1} -1)}$${\ Displaystyle \ razy}$${\ Displaystyle (M_ {2} -1)}$ .
3. Zero pad ${\ Displaystyle h (n_ {1}, n_ {2})}$ tak, że ma wymiary ( ${\ Displaystyle L_ {1} + M_ {1} } -1}$ ) ${\ Displaystyle \ razy}$ ( ${\ Displaystyle L_ {2} + M_ {2} -1}$ ).
4. Użyj DFT, aby uzyskać ${\ Displaystyle H (k_ {1}, k_ {2})}$ .
5. Dla każdego bloku wejściowego:
   1. Weź dyskretną transformatę Fouriera każdego bloku, aby dać ${\ Displaystyle X_ {ij} (k_ {1}, k_ {2})}$ .
   2. $(k_ {1}, k_ {2}) =X_{ij}(k_{1},k_{2})H(k_{1},k_{2})}$ jot .
   3. Weźmy odwrotną dyskretną transformatę Fouriera ${\ Displaystyle Y_ {ij} (k_ {1}, k_ {2})}$ , aby uzyskać ${\ Displaystyle y_{ij}(n_{1},n_{2})}$ .
   4. Pozbądź się pierwszego ${\ Displaystyle (M_ {1} -1)}$${\ Displaystyle \ razy}$ ( $\ Displaystyle (M_ {2} -1)}$ blok wyjściowy ${\ Displaystyle y_ {ij} (n_ {1}, n_ {2})}$ .
6. Znajdź ${\ Displaystyle y (n_ {1}, n_ {2})}$ , dołączając ostatni ${\ Displaystyle (L_ {1} \ razy L_ {2} )}$ próbki dla każdego bloku wyjściowego ${\ Displaystyle y_ {ij} (n_ {1}, n_ {2})}$ .

Transformacja helisy

Podobnie jak w przypadku dekompozycji wiersz-kolumna, transformacja helisy oblicza wielowymiarowy splot poprzez włączenie jednowymiarowych właściwości splotu i operatorów. Jednak zamiast wykorzystywać separowalność sygnałów, odwzorowuje kartezjańską przestrzeń współrzędnych na helikalną przestrzeń współrzędnych, umożliwiając mapowanie z przestrzeni wielowymiarowej do przestrzeni jednowymiarowej.

Splot wielowymiarowy z jednowymiarowymi metodami splotu

Aby zrozumieć transformację helisy, warto najpierw zrozumieć, w jaki sposób splot wielowymiarowy można podzielić na splot jednowymiarowy. Załóżmy, że dwa sygnały do ​​splotu to Y $,$$\ Displaystyle Y_ {K \ razy L}$ wyjściem ${\ Displaystyle Z_ {(MK + 1) \ razy (NL + 1)}}$ . Wyraża się to następująco:

${\ Displaystyle Z (i, j) = \ suma _ {m =0}^{M-1}\suma _{n=0}^{N-1}X(m,n)Y(im,jn)}$

Następnie tworzone są dwie macierze, które zerują każde wejście w obu wymiarach, tak aby każde wejście miało równoważne wymiary, tj

${\ Displaystyle \ mathbf {X '} = {\ początek {bmatrix} X&0 \\0 i 0 \\\ koniec {bmatrix}}}$ i ${\ Displaystyle \ mathbf {Y' } ={\begin{bmacierz}Y&0\\0&0\\\koniec{bmacierzy}}}$

gdzie każda z macierzy wejściowych ma teraz wymiary ${\ Displaystyle (M + K-1)}$${\ Displaystyle \ razy}$${\ Displaystyle (N + L- 1)}$ . Możliwe jest $''}$ zaimplementowanie porządkowania leksykograficznego w kolumnach w celu konwersji zmodyfikowanych macierzy na wektory { $X$ . Aby zminimalizować liczbę nieistotnych próbek w każdym wektorze, każdy wektor jest obcinany po ostatniej próbce $w$$i$ odpowiednio . Biorąc to pod uwagę, długość wektora i ${\ displaystyle Y''}$ są podane przez: ${\ displaystyle X''}$

${\ Displaystyle l_ {X''} =}$${\ Displaystyle (M + K-1)}$${\ Displaystyle \ razy}$${\ Displaystyle (N -1)}$ + ${\ displaystyle M}$

${\ Displaystyle l_ {Y''} =}$${\ Displaystyle (M + K-1)}$${\ Displaystyle \ razy}$${\ Displaystyle (L -1)}$ + ${\ Displaystyle K}$

Długość splotu tych dwóch wektorów można wyprowadzić i pokazać, że wynosi: ${\ displaystyle Z''}$

${\ Displaystyle l_ {Z''} =}$${\ Displaystyle l_ {Y''} +}$${\ Displaystyle l_ {X''}}$${\ Displaystyle = (M + K-1)}$${\ Displaystyle \ razy}$${\ Displaystyle (N + L-1)}$

Ta długość wektora jest równoważna wymiarom oryginalnego wyjścia macierzy $,$ że konwersja z powrotem do macierzy jest bezpośrednią transformacją. W ten sposób wektor $macierzowej , co$ wynik dwuwymiarowego dyskretnego splotu

Filtrowanie po helisie

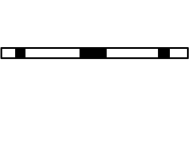
Podczas pracy z dwuwymiarową siatką kartezjańską transformata Fouriera wzdłuż obu osi spowoduje, że dwuwymiarowa płaszczyzna stanie się walcem, gdy koniec każdej kolumny lub rzędu zostanie przymocowany do odpowiedniego wierzchołka, tworząc cylinder. Filtrowanie po helisie zachowuje się w podobny sposób, z wyjątkiem tego przypadku, gdy dolna część każdej kolumny łączy się z górną częścią następnej kolumny, co daje spiralną siatkę. Jest to zilustrowane poniżej. Ciemne kafelki reprezentują współczynniki filtra.

Transformacja z dwuwymiarowej płaszczyzny filtra kartezjańskiego do filtra helisy.

Jeśli ta helikalna struktura zostanie następnie pocięta i rozwinięta w jednowymiarowy pasek, te same współczynniki filtra na 2-d płaszczyźnie kartezjańskiej będą pasować do tych samych danych wejściowych, co daje równoważny schemat filtrowania. Zapewnia to, że dwuwymiarowy splot będzie mógł zostać wykonany przez jednowymiarowego operatora splotu, ponieważ filtr 2D został rozwinięty do filtra 1D z przerwami zerowymi oddzielającymi współczynniki filtra.

Jednowymiarowy pasek filtrujący po rozwinięciu.

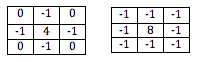
Zakładając, że zastosowano jakiś dwuwymiarowy filtr dolnoprzepustowy, taki jak:

0	-1	0
-1	4	-1
0	-1	0

Następnie, po przekształceniu przestrzeni dwuwymiarowej w helisę, filtr jednowymiarowy wyglądałby następująco:

${\ Displaystyle h (n) = -1,0,...,0,-1,4,-1,0,...,0,-1,0,...}$

Należy zauważyć, że w jednowymiarowym filtrze nie ma wiodących zer, jak pokazano na jednowymiarowym pasku filtrującym po rozwinięciu. Cały jednowymiarowy pasek mógł być skręcony; jednak po prostu ignorowanie wiodących zer jest mniej kosztowne obliczeniowo. Ponadto żadna z tych odwrotnych wartości zerowych nie będzie musiała być przechowywana w pamięci, co pozwoli zachować cenne zasoby pamięci.

Aplikacje

Transformacje helisy do implementacji filtrów rekurencyjnych poprzez splot są wykorzystywane w różnych obszarach przetwarzania sygnałów. Chociaż analiza Fouriera w dziedzinie częstotliwości jest skuteczna, gdy systemy są stacjonarne, ze stałymi współczynnikami i okresowo próbkowanymi danymi, staje się trudniejsza w systemach niestabilnych. Transformacja helisy umożliwia trójwymiarowe procesy migracji po stosie, które mogą przetwarzać dane dla trójwymiarowych zmian prędkości. Ponadto można go zastosować do rozwiązania problemu niejawnej trójwymiarowej ekstrapolacji pola falowego. Inne zastosowania obejmują pomocne algorytmy w regularyzacji danych sejsmicznych, filtry błędów przewidywania i tłumienie szumów w geofizycznych systemach cyfrowych.

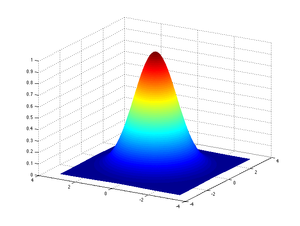
Splot Gaussa

Jednym z zastosowań splotu wielowymiarowego, który jest używany w przetwarzaniu sygnałów i obrazów, jest splot Gaussa. Odnosi się to do splatania sygnału wejściowego z funkcją rozkładu Gaussa.

${\ Displaystyle \ mu _ {1} = \ mu _ {2} = 0}$$\ sigma _ {2}=1}$ { =

Rozkład Gaussa próbkowany przy wartościach dyskretnych w jednym wymiarze jest określony następująco (przy założeniu): ${\ displaystyle \ mu = 0}$ :

$${\ Displaystyle G (n) = {\ Frac {1} {\ sqrt {2 \ pi \ sigma ^ {2}}}} e ^ { -{\frac {n^{2}}{2\sigma ^{2}}}}}$$

$\ Displaystyle \ mu _ {1} = \ mu _{2}=...=\mu _{M}=0}$ to łatwo rozszerzyć na sygnał o $wymiarach$ M (zakładając, że stały dla wszystkich wymiarów i ):

$${\ Displaystyle G (n_ {1}, n_ {2}, ..., n_ {M}) = {\ Frac {1} {(2 \ pi) ^ {M / 2} \ sigma ^ {M}} }e^{-{\frac {({n_{1}}^{2}+{n_{2}}^{2}+...+{n_{M}}^{2})}{2 \sigma ^{2}}}}}$$

Jedną z ważnych właściwości do rozpoznania jest to, że sygnał wymiarowy M jest rozdzielny, tak że:

$${\ Displaystyle G (n_ {1}, n_ {2}, ..., n_ {M}) = G (n_ {1}) G (n_ {2}) ... G (n_ {M})}$$

Następnie splot Gaussa z sygnałami o wartościach dyskretnych można wyrazić następująco:

${\ Displaystyle y (n) = x (n) * G (n)}$

${\ Displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}, n_ {2}, ..., n_ {M}) * ... *G(n_{1},n_{2},...,n_{M})}$

Aproksymacja przez filtr FIR

Splot Gaussa można skutecznie aproksymować poprzez implementację filtra skończonej odpowiedzi impulsowej (FIR). Filtr zostanie zaprojektowany z obciętymi wersjami Gaussa. W przypadku filtra dwuwymiarowego funkcja przenoszenia takiego filtra byłaby zdefiniowana następująco:

${\ Displaystyle H (z_ {1}, z_ {2}) = {\ Frac {1} {s (r_ {1}, r_ {2})}} \ suma _ {n_ {1} = - r_ { 1}}^{r_{1}}\suma _{n_{2}=-r_{2}}^{r_{2}}G(n_{1},n_{2}){z_{1}} ^{-n_{1}}{z_{2}}^{-n_{2}}}$

Gdzie

${\ Displaystyle s (r_ {1}, r_ {2}) =\suma _{n_{1}=-r_{1}}^{r_{1}}\suma _{n_{2}=-r_{2}}^{r_{2}}G(n_{1 },n_{2})}$

Wybór niższych wartości dla i ${$$\ displaystyle r_ {2}}$ spowoduje wykonanie mniejszej liczby obliczeń, ale da mniej dokładne przybliżenie, podczas gdy wybranie wyższych wartości da dokładniejsze przybliżenie, r 1 {\ displaystyle r_ ale będzie wymagać większej liczby obliczeń.

Aproksymacja za pomocą filtra pudełkowego

Inną metodą aproksymacji splotu Gaussa są rekurencyjne przejścia przez filtr skrzynkowy. W celu aproksymacji splotu jednowymiarowego filtr ten jest zdefiniowany w następujący sposób:

${\ Displaystyle H (z) = {\ Frac {1} {2r + 1}} {\ Frac {z ^ { r}-z^{-r-1}}{1-z^{-}1}}}$

Zazwyczaj rekurencyjne przejścia są wykonywane 3, 4 lub 5 razy w celu uzyskania dokładnego przybliżenia. Sugerowana metoda obliczania r jest wtedy następująca:

${\ Displaystyle \ sigma ^ {2} = {\ Frac {1} {12}} K ((2r + 1) ^ {2} -1 )}$ gdzie K jest liczbą przejść rekurencyjnych przez filtr.

Następnie, ponieważ rozkład Gaussa można rozdzielić w różnych wymiarach, wynika z tego, że rekurencyjne przejścia przez filtry jednowymiarowe (izolujące każdy wymiar osobno) dadzą w ten sposób przybliżenie wielowymiarowego splotu Gaussa. Oznacza to, że M- wymiarowy splot Gaussa można aproksymować za pomocą rekurencyjnych przejść przez następujące jednowymiarowe filtry:

${\ Displaystyle H (z_ {1}) = {\ Frac {1} {2r_ { 1}+1}}{\frac {{z_{1}}^{r_{1}}-{z_{1}}^{-r_{1}-1}}{1-{z_{1}} ^{-}1}}}$

${\ Displaystyle H (z_ {2}) = {\ Frac {1} {2r_ { 2}+1}}{\frac {{z_{2}}^{r_{2}}-{z_{2}}^{-r_{2}-1}}{1-{z_{2}} ^{-}1}}}$

${\ Displaystyle \ vdots}$

${\ Displaystyle H (z_ {M}) = {\ Frac {1} {2r_ { M}+1}}{\frac {{z_{M}}^{r_{M}}-{z_{M}}^{-r_{M}-1}}{1-{z_{M}} ^{-}1}}}$

Aplikacje

Sploty gaussowskie są szeroko stosowane w przetwarzaniu sygnałów i obrazów. Na przykład rozmycie obrazu można osiągnąć za pomocą splotu gaussowskiego, w którym $parametr$ kontrolował siłę rozmycia. Wyższe wartości odpowiadałyby zatem bardziej rozmytemu wynikowi końcowemu. Jest również powszechnie używany w komputerowych aplikacjach wizyjnych, takich jak wykrywanie funkcji transformacji funkcji niezmiennej w skali (SIFT).

Zobacz też

• Skręt
• Jądro (przetwarzanie obrazu)
• Przetwarzanie sygnałów