Kości Miwina

Kości Miwina
Miwin Wuerfel Titan.gif
Kości Miwina wykonane z tytanu
Projektanci dr Michaela Winkelmanna
Wydawcy Arquus Verlag Wiedeń
lata aktywności 1994
Gracze 1–9
Czas odtwarzania 5–60 minut, w zależności od gry
Zakres wieku 6+, w zależności od gry
Strona internetowa www.miwin.com

Kości Miwina to zestaw nieprzechodnich kości wynaleziony w 1975 roku przez fizyka Michaela Winkelmanna. Składają się z trzech różnych kostek o ściankach z liczbami od jednego do dziewięciu; przeciwległe twarze sumują się do dziewięciu, dziesięciu lub jedenastu. Liczby na każdej kostce dają sumę 30 i mają średnią arytmetyczną pięć.

Opis

Kostka Miwinsa IX, X, XI

Kości Miwina mają sześć boków, z których każdy ma numer przedstawiony we wzorze kropek. Standardowy zestaw wykonany jest z drewna; specjalne konstrukcje wykonane są z tytanu lub innych materiałów (złoto, srebro).

Pierwszy zestaw kości Miwina: III, IV, V

projekt numerów kostek Miwinsa III, IV, V

Każda kość nosi nazwę sumy jej dwóch najniższych liczb. Kropki na każdej kostce są koloru niebieskiego, czerwonego lub czarnego. Każda kość ma następujące numery:

Umrzeć III z czerwonymi kropkami 1 2 5 6 7 9
Umrzeć IV z niebieskimi kropkami 1 3 4 5 8 9
umrzeć V z czarnymi kropkami 2 3 4 6 7 8  

Liczby 1 i 9, 2 i 7 oraz 3 i 8 znajdują się po przeciwnych stronach wszystkich trzech kostek. Dodatkowe liczby to 5 i 6 na kostce III, 4 i 5 na kostce IV oraz 4 i 6 na kostce V. Kostki są zaprojektowane w taki sposób, że dla każdej kości inna zazwyczaj wygrywa z nią. Prawdopodobieństwo że dana kostka w sekwencji (III, IV, V, III) wyrzuci wyższą liczbę niż następna w sekwencji, wynosi 17/36; niższa liczba, 16/36. Zatem kość III ma tendencję do wygrywania z IV, IV z V i V z III. Takie kości są znane jako nieprzechodnie .

Drugi zestaw kości Miwina: IX, X, XI

projekt numerów kostek Miwinsa IX, X, XI

Każda kość nosi nazwę sumy jej najniższych i najwyższych liczb. Kropki na każdej kostce są koloru żółtego, białego lub zielonego. Każda kość ma następujące numery:

Umrzeć IX z żółtymi kropkami 1 3 5 6 7 8
Umrzeć X z białymi kropkami 1 2 4 6 8 9
Umrzeć XI z zielonymi kropkami 2 3 4 5 7 9

Prawdopodobieństwo , że dana kostka w sekwencji (XI, X, IX, XI) wyrzuci wyższą liczbę niż następna w sekwencji, wynosi 17/36; niższa liczba, 16/36. Zatem kostka XI ma tendencję do wygrywania z X, X z IX, a IX z XI.

Trzeci i czwarty zestaw kości Miwina

Trzeci zestaw:

Die MW 5 z niebieskimi cyframi 5 6 7 8 15 16
Die MW 3 z czerwonymi cyframi 3 4 11 12 13 14
Die MW 1 z czarnymi cyframi 1 2 9 10 17 18

czwarty zestaw:

Die MW 6 z żółtymi cyframi 5 6 9 10 13 14
Die MW 4 z białymi cyframi 3 4 7 8 17 18
Die MW 2 z zielonymi cyframi 1 2 11 12 15 16

Prawdopodobieństwo , że dana kostka w pierwszej sekwencji (5, 3, 1, 5) lub drugiej sekwencji (6, 4, 2, 6) wyrzuci wyższą liczbę niż kolejna w sekwencji, wynosi 5/9; niższa liczba, 4/9.

Atrybuty matematyczne

Kości w pierwszym i drugim zestawie Miwina mają podobne cechy: każda kostka nosi każdą z liczb dokładnie raz, suma liczb wynosi 30, a każda liczba od jednego do dziewięciu jest rozłożona dwukrotnie na trzech kostkach. Atrybut ten charakteryzuje implementację kości nieprzechodnich, umożliwiających różne warianty gry. Wszystkie gry wymagają tylko trzech kości, w porównaniu do innych teoretycznych kości nieprzechodnich, zaprojektowanych z myślą o matematyce, takich jak kości Efrona .

Prawdopodobieństwa

  • 1/3 wartości matrycy można podzielić przez trzy bez przenoszenia.
  • 1/3 wartości matrycy można podzielić przez trzy z przeniesieniem jednego.
  • 1/3 wartości matrycy można podzielić przez trzy z przeniesieniem dwóch.

Prawdopodobieństwo dla danej liczby wszystkimi trzema kośćmi wynosi 11/36, dla danego wyrzuconego podwójnego wynosi 1/36, dla dowolnego wyrzuconego podwójnego 1/4. Prawdopodobieństwo uzyskania podwójnego wyniku wynosi tylko 50% w porównaniu do zwykłych kości.

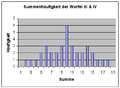
Częstotliwość skumulowana

  • Cumulative frequency type III and IV

    Skumulowana częstotliwość typu III i IV

  • Cumulative frequency type III and V

    Skumulowana częstotliwość typu III i V

  • Cumulative frequency type IV and V

    Typ częstotliwości skumulowanej IV i V

  • Cumulative frequency type III and IV and V = "Miwin-Distribution"

    Typ częstotliwości skumulowanej III i IV oraz V = „Miwin-Distribution”

Odwrócona nieprzechodniość

Usunięcie wspólnych kropek Miwin's Dice odwraca nieprzechodniość. [ potrzebne źródło ]

Umrzeć III z niebieskimi kropkami 1 2 5 6 7 9 → Umrzeć III' 2 6 7
Umrzeć IV z czerwonymi kropkami 1 3 4 5 8 9 → Śmierć IV' 3 4 8 
III:IV = 17:16, III':IV' = 4:5 → IV' > III' analog: III/V, IV/V

Równy rozkład liczb losowych

Kostki Miwina umożliwiają losowe generowanie liczb w zadanym zakresie, tak aby każda zawarta w nich liczba miała jednakowe prawdopodobieństwo wystąpienia. Aby uzyskać zakres, który nie zaczyna się od 1 lub 0, po prostu dodaj stałą wartość, aby sprowadzić go do tego zakresu (aby uzyskać liczby losowe z przedziału od 8 do 16 włącznie, postępuj zgodnie z poniższymi instrukcjami od 1 do 9 i dodaj siedem do wynik każdego rzutu).

  • 1 – 9 : Rzuca się 1 kostką (wybieraną losowo): P(1) = P(2) = ... = P(9) = 1/9
  • 0 – 80 : Rzuca się 2 kostkami (wybieranymi losowo), zawsze odejmuje się 1: P(0) = P(1) = ... = P(80) = 1/9² = 1/81

Inne dystrybucje

0 – 90 (rzuć 3 razy)

Rządzące prawdopodobieństwo: P(0) = P(1) = ... = P(90) = 8/9³ = 8/729

Aby uzyskać równy rozkład liczb od 0 do 90, rzuca się wszystkimi trzema kośćmi, po jednej na raz, w przypadkowej kolejności. Wynik obliczany jest w oparciu o następujące zasady:

  • Pierwszy rzut to 9, trzeci rzut to nie 9: daje 10 razy Drugi rzut (możliwe wyniki: 10, 20, 30, 40, 50, 60, 70, 80, 90)
  • Pierwszy rzut to nie 9: daje 10 razy pierwszy rzut plus drugi rzut
  • 1. rzut jest równy 3. rzutowi: daje 2. rzut (możliwe wyniki: 1, 2, 3, 4, 5, 6, 7, 8, 9)
  • Wszystkie kości są równe: daje 0
  • Wszystkie kości 9: brak wyniku

Próbka:

1. rzut 2. rzut trzeci rzut Równanie Wynik
9 9 nie 9 10 razy 9 90
9 1 nie 9 10 razy 1 10
8 4 nie 8 (10 razy 8) + 4 84
1 3 nie 1 (10 razy 1) + 3 13
7 8 7 7 = 7, daje 8 8
4 4 4 wszyscy równi 0
9 9 9 wszystkie 9 -

Daje to 91 liczb, od 0 – 90 z prawdopodobieństwem 8 / 9³, 8 × 91 = 728 = 9³ − 1

0 – 103 (rzuć 3 razy)

Rządzące prawdopodobieństwo: P(0) = P(1) = ... = P(103) = 7/9³ = 7/729

Daje to 104 liczby od 0 – 103 z prawdopodobieństwem 7 / 9³, 7 × 104 = 728 = 9³ − 1

0 – 728 (rzuć 3 razy)

Rządzące prawdopodobieństwo: P(0) = P(1) = ... = P(728) = 1 / 9³ = 1 / 729

Daje to 729 liczb, od 0 do 728, z prawdopodobieństwem 1/9³.

Jednorazowo rzuca się jedną kostką, wybieraną losowo.

Utwórz system liczbowy o podstawie 9:

  • 1 należy odjąć od wartości nominalnej każdego rzutu, ponieważ w tym systemie liczbowym jest tylko 9 cyfr (0,1,2,3,4,5,6,7,8)
  • (pierwszy rzut) × 81 + (drugi rzut) × 9 + (trzeci rzut) × 1

Ten system daje to maksimum: 8 × 9² + 8 × 9 + 8 × 9 ° = 648 + 72 + 8 = 728 = 9³ - 1

Przykłady:

1. rzut 2. rzut trzeci rzut Równanie Wynik
9 9 9 8 × 9² + 8 × 9 + 8 728
4 7 2 3 × 9² + 6 × 9 + 1 298
2 4 1 1 × 9² + 4 × 9 + 0 117
1 3 4 0 × 9² + 3 × 9 + 3 30
7 7 7 6 × 9² + 6 × 9 + 6 546
1 1 1 0 × 9² + 0 × 9 + 0 0
4 2 6 3 × 9² + 1 × 9 + 5 257

Kombinacje z kośćmi Miwina typu III, IV i V

Wariant Równanie liczba wariantów
jeden rzut 3 kośćmi, typ nie jest używany jako atrybut - 135
jeden rzut 3 kośćmi, typ jest dodatkowym atrybutem (135 – 6 × 9) × 2 + 54 216
1 rzut z każdym typem, typ nie jest używany jako atrybut 6 × 6 × 6 216
1 rzut z każdym typem, typ jest używany jako atrybut 6 × 6 × 6 × 6 1296
3 rzuty, losowy wybór jednej z kości do każdego rzutu, typ nie jest używany jako atrybut 9 × 9 × 9 729

3 rzuty, losowy wybór jednej z kostek do każdego rzutu, typ jest używany jako atrybut:

Wariant Równanie liczba alternatyw
III, III, III/IV, IV, IV/V, V, V 3 × 6 × 6 × 6 648
III, III, IV/III, III, V/III, IV, IV/III, V, V/IV, IV, V/IV, V, V 6 × 3 × 216 + 3888
III, IV, V/III, V, IV/IV, III, V/IV, V, III/V, III, IV/V, IV, III 6 × 216 + 1296
= 5832

Możliwe są liczby 5832 = 2 × 2 × 2 × 9 × 9 × 9 = 18³.

Gry

Od połowy lat 80. o igrzyskach pisała prasa. Sam Winkelmann prezentował gry m.in. w 1987 roku w Wiedniu na „Österrechischen Spielefest, Stiftung Spielen in Österreich”, Leopoldsdorf, gdzie „Kości Miwina” zdobyły nagrodę „Novel Independent Dice Game of the Year”.

W 1989 roku gry zostały zrecenzowane przez czasopismo „Die Spielwiese”. W tym czasie istniało 14 alternatyw gier hazardowych i strategicznych dla kości Miwina. Czasopismo „Spielbox” miało dwa warianty gry w kości Miwina w kategorii „Unser Spiel im Heft” (obecnie znanej jako „Edition Spielbox”): pasjans 5 do 4 oraz strategiczna gra dla dwóch graczy Bitis .

W 1994 roku wiedeńskie wydawnictwo Arquus wydało książkę Winkelmanna Göttliche Spiele , która zawierała 92 gry, kopię wzorcową czterech plansz do gry, dokumentację dotyczącą matematycznych atrybutów kości oraz zestaw kości Miwina. Istnieje jeszcze więcej wariantów gry wymienionych na stronie internetowej Winkelmanna.

Opracowano gry Solitaire i gry dla maksymalnie dziewięciu graczy. Gry są odpowiednie dla graczy powyżej szóstego roku życia. Niektóre gry wymagają planszy; czas gry waha się od 5 do 60 minut.

Warianty 0 – 80

1. wariant

Rzuca się dwiema kośćmi, wybieranymi losowo, po jednej na raz. Każda para jest punktowana przez pomnożenie pierwszej przez dziewięć i odjęcie drugiej od wyniku: 1. rzut × 9 - 2. rzut.

Przykłady:

1. rzut 2. rzut Równanie Wynik
9 9 9 × 9 - 9 72
9 1 9 × 9 - 1 80
1 9 9 × 1 - 9 0
2 9 9 × 2 - 9 9
2 8 9 × 2 - 8 10
8 4 9 × 8 - 4 68
1 3 9 × 1 - 3 6

Ten wariant dostarcza liczb od 0 do 80 z prawdopodobieństwem 1 / 9² = 1 / 81.

2. wariant

Rzuca się dwiema kośćmi, wybieranymi losowo, po jednej na raz. Para jest punktowana zgodnie z następującymi zasadami:

  • Pierwszy rzut to 9: daje 10 × drugi rzut − 10
  • Pierwszy rzut to nie 9: daje 10 × pierwszy rzut + drugi rzut - 10
Przykłady
1. rzut 2. rzut Równanie Wynik
9 9 10 × 9 - 10 80
9 1 10 × 1 - 10 0
8 4 10 × 8 + 4 − 10 74
1 3 10 × 1 + 3 − 10 3

Ten wariant dostarcza liczb od 0 do 80 z prawdopodobieństwem 1 / 9² = 1 / 81.

3. wariant

Rzuca się dwiema kośćmi, wybieranymi losowo, po jednej na raz. Punktację uzyskuje się według następujących zasad:

  • Oba rzuty to 9: daje 0
  • Pierwszy rzut to 9, a drugi rzut to nie 9: daje 10 × drugi rzut
  • Pierwszy rzut to 8: daje drugi rzut
  • Wszyscy inni: daje 10 × 1. rzut - 2. rzut

Przykłady:

1. rzut 2. rzut Równanie Wynik
9 9 - 0
9 3 10 × 3 30
8 4 1 × 4 4
5 9 5 × 10 + 9 59

Notatki

  1. ^ http://www.miwin.com/ kliknij „Miwin'sche Würfel 2”, a następnie sprawdź atrybuty
  2. Bibliografia _
  3. ^ 29/1989 strona 6
  4. ^ Książka o niemieckiej wersji Amazon
  5. ^ Strona domowa Winkelmanna

Linki zewnętrzne

Opublikowane gry

  •   Friedhelm Merz: Spiel '89. Książka dla Hazardzistów, Twórców Gier, Producentów Gier i Prasy . Merz Verl., Bonn 1989, ISBN 3-926108-23-1 , S. 477.
  •   Michael Winkelmann: Göttliche Spiele Arquus-Verl. Pahlich 1994 Göttliche Spiele Arquus-Verl. Pahlich 1994, ISBN 3-901388-10-9 ,
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Miwin%27s_dice&oldid=1110020710 ”