Kości nieprzechodnie

Zestaw kości jest nieprzechodni (lub nieprzechodni), jeśli zawiera trzy kości, A , B i C , z tą właściwością, że A wypada wyżej niż B przez ponad połowę czasu, a B rzuca wyżej niż C przez ponad połowę czasu, ale nie jest prawdą, że A wypada wyżej niż C w ponad połowie przypadków. Innymi słowy, zestaw kostek jest nieprzechodni, jeśli relacja binarna – $X$ wyrzuci liczbę wyższą niż $Y$ przez ponad połowę czasu – na swoich elementach nie jest przechodnia . Mówiąc prościej, A normalnie bije B , B normalnie bije C , ale A normalnie nie bije C .

Można znaleźć zestawy kości o jeszcze silniejszej właściwości polegającej na tym, że dla każdej kości w zestawie jest inna kostka, która rzuca wyższą liczbą niż ona w ponad połowie przypadków. Różni się to tym, że zamiast tylko „ A zwykle nie pokonuje C ”, jest teraz „ C normalnie pokonuje A” . Używając takiego zestawu kości, można wymyślać gry, które są stronnicze w sposób, którego ludzie nieprzyzwyczajeni do nieprzechodnich kości mogą się nie spodziewać (patrz Przykład ).

Przykład

Przykład kości nieprzechodnich (przeciwne strony mają taką samą wartość jak te pokazane).

Rozważ następujący zestaw kości.

Kostka A ma boki 2, 2, 4, 4, 9, 9.
Kostka B ma boki 1, 1, 6, 6, 8, 8.
Kostka C ma boki 3, 3, 5, 5, 7, 7.

Prawdopodobieństwo , że A wyrzuci więcej niż B , prawdopodobieństwo, że B wyrzuci więcej niż C , i prawdopodobieństwo, że C wyrzuci więcej niż A wynoszą 5 / 9 , więc ten zestaw kości jest nieprzechodni. W rzeczywistości ma jeszcze silniejszą właściwość, że dla każdej kości w zestawie jest inna kostka, która rzuca wyższą liczbą niż ona w ponad połowie przypadków.

Rozważmy teraz następującą grę, w którą gra się zestawem kości.

Pierwszy gracz wybiera kość z zestawu.
Drugi gracz wybiera jedną kość z pozostałych kości.
Obaj gracze rzucają swoimi kostkami; gracz, który wyrzuci wyższą liczbę, wygrywa.

Jeśli ta gra jest rozgrywana z przechodnim zestawem kości, jest albo sprawiedliwa, albo stronnicza na korzyść pierwszego gracza, ponieważ pierwszy gracz zawsze może znaleźć kość, której nie pokona żadna inna kość przez więcej niż połowę czasu. Jeśli jednak gra się z zestawem kości opisanym powyżej, gra jest przesunięta na korzyść drugiego gracza, ponieważ drugi gracz zawsze może znaleźć kość, która przebije kość pierwszego gracza z prawdopodobieństwem 5 / 9 . Poniższe tabele przedstawiają wszystkie możliwe wyniki dla wszystkich trzech par kości.

A C	2	4	9	B A	1	6	8	C B	3	5	7
Gracz 1 wybiera kość Gracz 2 wybiera kość C				Gracz 1 wybiera kość B Gracz 2 wybiera kość A				Gracz 1 wybiera kość C Gracz 2 wybiera kość B
3	C	A	A	2	A	B	B	1	C	C	C
5	C	C	A	4	A	B	B	6	B	B	C
7	C	C	A	9	A	A	A	8	B	B	B

Komentarz dotyczący równoważności kości nieprzechodnich

Chociaż trzy nieprzechodnie kości A, B, C (pierwszy zestaw kości)

O: 2, 2, 6, 6, 7, 7
B: 1, 1, 5, 5, 9, 9
C: 3, 3, 4, 4, 8, 8

P(A > B) = P(B > C) = P(C > A) = 5 / 9

oraz trzy nieprzechodnie kości A′, B′, C′ (drugi zestaw kości)

A′: 2, 2, 4, 4, 9, 9
B′: 1, 1, 6, 6, 8, 8
C′: 3, 3, 5, 5, 7, 7

P(A′ > B′) = P(B′ > C′) = P(C′ > A′) = 5 / 9

wygrają ze sobą z równym prawdopodobieństwem, nie są równoważne. Podczas gdy pierwszy zestaw kości (A, B, C) ma „najwyższą” kość, drugi zestaw kości ma „najniższą” kość. Rzucenie trzema kośćmi z zestawu i zawsze używanie najwyższego wyniku do oceny pokaże inny wzór wygranej dla dwóch zestawów kości. 8/27 Przy pierwszym zestawie kości kostka , 11/27 ), a kości B wygra z najwyższym prawdopodobieństwem ( A i C wygrają z prawdopodobieństwem . Przy drugim zestawie kostek kostka C′ wygra z najmniejszym prawdopodobieństwem ( 7 / 27 ) i kości A′ i B′ wygrają z prawdopodobieństwem 10 / 27 .

Wariacje

Kości Efrona

Kości Efrona to zestaw czterech nieprzechodnich kości wymyślonych przez Bradleya Efrona .

Przedstawienie kości Efrona

Cztery kości A, B, C, D mają na sześciu ściankach następujące liczby:

O: 4, 4, 4, 4, 0, 0
B: 3, 3, 3, 3, 3, 3
C: 6, 6, 2, 2, 2, 2
D: 5, 5, 5, 1, 1, 1

Prawdopodobieństwa

2/3 kość jest lepsza od poprzedniej z listy z prawdopodobieństwem :

{\ Displaystyle P (A> B) = P (B> C) = P (C >D)=P(D>A)={2 \ponad 3}}

Drzewo prawdopodobieństwa warunkowego można wykorzystać do określenia prawdopodobieństwa, z jakim C wypadnie wyżej niż D.

wartość B jest stała; A bije go na 2 / 3 rzuty, ponieważ cztery z jego sześciu ścian są wyższe.

Podobnie B pokonuje C z prawdopodobieństwem 2/3 , ponieważ tylko dwie ściany C są wyższe.

P(C>D) można obliczyć, sumując prawdopodobieństwa warunkowe dla dwóch zdarzeń:

Rzuty C 6 (prawdopodobieństwo 1 / 3 ); wygrywa niezależnie od D (prawdopodobieństwo 1)
C rzuca 2 (prawdopodobieństwo 2 / 3 ); wygrywa tylko wtedy, gdy D wyrzuci 1 (prawdopodobieństwo 1 / 2 )

Całkowite prawdopodobieństwo wygranej dla C wynosi zatem

{\ Displaystyle \ lewo ({1 \ ponad 3} \ razy 1 \ prawo) + \ lewo ({2 \ ponad 3} \ razy {1 \ ponad 2}\prawo)={2 \ponad 3}}

Przy podobnych obliczeniach prawdopodobieństwo, że D wygra z A, wynosi

{\ Displaystyle \ lewo ({1 \ ponad 2} \ razy 1 \ prawo) + \ lewo ({1 \ ponad 2} \ razy {1 \ ponad 3}\prawo)={2 \ponad 3}}

Najlepsza ogólna śmierć

Cztery kości mają nierówne prawdopodobieństwo trafienia kości wybranej losowo z pozostałych trzech:

Jak udowodniono powyżej, kostka A pokonuje B w dwóch trzecich przypadków, ale pokonuje D tylko w jednej trzeciej. Prawdopodobieństwo, że kostka A pokona C wynosi 4/9 . , (A musi wyrzucić 4 a C musi wyrzucić 2) Tak więc prawdopodobieństwo, że A pokona dowolną inną losowo wybraną kostkę, wynosi:

{\ Displaystyle {1 \ ponad 3} \ razy \ lewo ({2 \ ponad 3} + {1 \ ponad 3} + {4 \ ponad 9} \right)={13 \ponad 27}}

Podobnie kostka B pokonuje C w dwóch trzecich przypadków, ale pokonuje A tylko w jednej trzeciej. Prawdopodobieństwo, że kostka B pokona D wynosi 1/2 , . ( tylko wtedy gdy D wyrzuci 1) Tak więc prawdopodobieństwo, że B pokona dowolną inną losowo wybraną kostkę, wynosi:

{\ Displaystyle {1 \ ponad 3} \ razy \ lewo ({2 \ ponad 3} + {1 \ ponad 3} + {1 \ ponad 2} \right)={1 \ponad 2}}

Die C pokonuje D w dwóch trzecich przypadków, ale pokonuje B tylko w jednej trzeciej. Prawdopodobieństwo, że kostka C pokona A wynosi 5/9 . Tak więc prawdopodobieństwo, że C pokona dowolną inną losowo wybraną kostkę, wynosi:

{\ Displaystyle {1 \ ponad 3} \ razy \ lewo ({2 \ ponad 3} + {1 \ ponad 3} + {5 \ ponad 9} \right)={14 \ponad 27}}

Wreszcie, kostka D pokonuje A w dwóch trzecich przypadków, ale pokonuje C tylko w jednej trzeciej. Prawdopodobieństwo, że kostka D pokona B, wynosi 1/2 . , ( tylko wtedy gdy D wyrzuci 5) Tak więc prawdopodobieństwo, że D pokona dowolną inną losowo wybraną kostkę, wynosi:

{\ Displaystyle {1 \ ponad 3} \ razy \ lewo ({2 \ ponad 3} + {1 \ ponad 3} + {1 \ ponad 2} \right)={1 \ponad 2}}

Dlatego najlepszą ogólną kostką jest C z prawdopodobieństwem wygranej 0,5185. C wyrzucił również najwyższą średnią liczbę w wartościach bezwzględnych, 3 + 1 / 3 . (Średnia A to 2 + 2 / 3 , podczas gdy B i D to 3.)

Warianty z równymi średnimi

Zauważ, że kości Efrona mają różne średnie rzuty: średni rzut A wynosi 8 / 3 , podczas gdy B i D mają średnio 9 / 3 , a C średnio 10 / 3 . Właściwość nieprzechodnia zależy od tego, które ściany są większe lub mniejsze, ale nie zależy od bezwzględnej wielkości ścian. Dlatego można znaleźć warianty kości Efrona, w których szanse na wygraną pozostają niezmienione, ale wszystkie kości mają taki sam średni rzut. Na przykład,

O: 7, 7, 7, 7, 1, 1
B: 5, 5, 5, 5, 5, 5
C: 9, 9, 3, 3, 3, 3
D: 8, 8, 8, 2, 2, 2

Te kości wariantów są przydatne np. do zapoznania uczniów z różnymi sposobami porównywania zmiennych losowych (oraz tego, jak porównanie samych średnich może przeoczyć istotne szczegóły).

Ponumerowane kości od 1 do 24

Zestaw czterech kości wykorzystujących wszystkie liczby od 1 do 24 można ustawić jako nieprzechodni. Przy sąsiednich parach prawdopodobieństwo wygranej na jednej kości wynosi 2/3.

Aby uzyskać wysoką liczbę, B bije A, C bije B, D bije C, A bije D.

00 O: 1, 2, 16, 17, 18, 19
000 B: 3, 4, 5, 20, 21, 22
0000 C: 6, 7, 8, 9, 23, 24
D: 10, 11, 12, 13, 14, 15

Związek z kośćmi Efrona

Te kości są w zasadzie takie same jak kości Efrona, ponieważ każdą liczbę z serii kolejnych liczb na jednej kostce można wszystkie zastąpić najniższą liczbą z serii, a następnie zmienić ich numerację.

O: 00 1, 2, 16, 17, 18, 19 → 00 1, 1, 16, 16, 16, 16 → 0, 0, 4, 4, 4, 4
B: 000 3, 4, 5, 20, 21, 22 → 000 3, 3, 3, 20, 20, 20 → 1, 1, 1, 5, 5, 5
C: 0000 6, 7, 8, 9, 23, 24 → 0000 6, 6, 6, 6, 23, 23 → 2, 2, 2, 2, 6, 6
D: 10, 11, 12, 13, 14, 15 → 10, 10, 10, 10, 10, 10 → 3, 3, 3, 3, 3, 3

Kości Miwina

Kości Miwina zostały wynalezione w 1975 roku przez fizyka Michaela Winkelmanna.

Rozważmy zestaw trzech kości, III, IV i V takich, że

kość III ma boki 1, 2, 5, 6, 7, 9
kość IV ma boki 1, 3, 4, 5, 8, 9
kostka V ma boki 2, 3, 4, 6, 7, 8

Następnie:

prawdopodobieństwo wynosi 17/36 , że III wyrzuci wyższą liczbę niż IV,
prawdopodobieństwo, że IV wyrzuci wyższą liczbę niż V wynosi 17/36
prawdopodobieństwo, że V wyrzuci wyższą liczbę niż III , wynosi 17/36

Zestaw trzech kości z minimalnymi zmianami w stosunku do standardowych kości

Następujące nieprzechodnie kości mają tylko kilka różnic w porównaniu ze standardowymi kośćmi od 1 do 6:

podobnie jak w przypadku standardowych kostek, całkowita liczba oczek wynosi zawsze 21
podobnie jak w przypadku standardowych kości, na bokach znajdują się tylko liczby oczek od 1 do 6
twarze z taką samą liczbą oczek występują maksymalnie dwa razy na kostce
tylko dwie strony każdej kości mają numery inne niż na standardowych kościach:
- O: 1, 1 , 3, 5 , 5, 6
- B: 2, 3, 3 , 4, 4 , 5
- K: 1, 2, 2 , 4, 6, 6

Podobnie jak zestaw Miwina, prawdopodobieństwo wygranej A kontra B (lub B vs. C, C vs. A) wynosi 17 / 36 . Prawdopodobieństwo remisu wynosi jednak 4 / 36 , więc tylko 15 z 36 rzutów jest przegranych. Więc ogólne oczekiwanie na wygraną jest wyższe.

Warrena Buffetta

Warren Buffett jest znany jako fan nieprzechodnich kości. W książce Fortune's Formula: The Untold Story of the Scientific Betting System that Beat the Casinos and Wall Street opisana jest dyskusja między nim a Edwardem Thorpem . Buffett i Thorp omówili wspólne zainteresowanie kośćmi nieprzechodnimi. „To matematyczna ciekawostka, rodzaj„ sztuczek ”kostek, które zakłócają wyobrażenia większości ludzi na temat prawdopodobieństwa”.

Buffett próbował kiedyś wygrać grę w kości z Billem Gatesem, używając nieprzechodnich kości. „Buffett zasugerował, aby każdy z nich wybrał jedną z kości, a następnie odrzucił pozostałe dwie. Założyliby się, kto najczęściej wyrzuci najwyższą liczbę. Buffett zaproponował, że Gates wybierze swoją kość jako pierwszy. Ta sugestia natychmiast wzbudziła ciekawość Gatesa. poprosił o zbadanie kości, po czym zażądał, aby Buffett wybrał pierwszy”.

W 2010 roku magazyn Wall Street Journal zacytował Sharon Osberg, brydżową partnerkę Buffetta, mówiąc, że kiedy po raz pierwszy odwiedziła jego biuro 20 lat wcześniej, oszukał ją do gry z nieprzechodnimi kośćmi, których nie można wygrać i „pomyślał, że to przezabawne”.

Zestaw nieprzechodnich kości dla więcej niż dwóch graczy

Wiele osób wprowadziło odmiany nieprzechodnich kości, w których można rywalizować z więcej niż jednym przeciwnikiem.

Trzech graczy

Kości Oskara

Oskar van Deventer przedstawił zestaw siedmiu kości (wszystkie ściany z prawdopodobieństwem 1 / 6 ) w następujący sposób:

0 O: 2, 2, 14, 14, 17, 17
0 B: 7, 7, 10, 10, 16, 16
0 C: 5, 5, 13, 13, 15, 15
000 D: 3, 3, 9, 9, 21, 21
0 E: 1, 1, 12, 12, 20, 20
000 F: 6, 6, 8, 8, 19, 19
0 G: 4, 4, 11, 11, 18, 18

Można sprawdzić, czy A bije {B,C,E}; B bije {C, D, F}; C bije {D, E, G}; D bije {A, E, F}; E bije {B, F, G}; F bije {A, C, G}; G bije {A, B, D}. W konsekwencji, dla dowolnie wybranych dwóch kości, istnieje trzecia, która bije je obie. Mianowicie,

G bije {A, B}; F bije {A, C}; G bije {A, D}; D bije {A, E}; D bije {A, F}; F bije {A, G};
A bije {B, C}; G bije {B, D}; A bije {B, E}; E bije {B, F}; E bije {B, G};
B bije {C, D}; A bije {C, E}; B bije {C, F}; F bije {C, G};
C bije {D, E}; B bije {D, F}; C bije {D, G};
D bije {E, F}; C bije {E, G};
E bije {F, G}.

Cokolwiek wybierze dwóch przeciwników, trzeci gracz znajdzie jedną z pozostałych kości, która przebije kości obu przeciwników.

Brudne kości

Dr James Grime odkrył zestaw pięciu kości w następujący sposób:

O: 2, 2, 2, 7, 7, 7
B: 1, 1, 6, 6, 6, 6
C: 0, 5, 5, 5, 5, 5
D: 4, 4, 4, 4, 4, 9
E: 3, 3, 3, 3, 8, 8

Można to sprawdzić, grając jednym zestawem kości Grime:

A bije B bije C bije D bije E bije A (pierwszy łańcuch);
A bije C bije E bije B bije D bije A (drugi łańcuch).

Jednakże, gdy gra toczy się dwoma takimi setami, pierwszy łańcuch pozostaje ten sam (z jednym wyjątkiem omówionym później), ale drugi łańcuch jest odwrócony (tzn. A bije D bije B bije E bije C bije A). W konsekwencji, niezależnie od tego, jakie kości wybiorą dwaj przeciwnicy, trzeci gracz zawsze może znaleźć jedną z pozostałych kości, która przebije ich obu (o ile gracz może wtedy wybrać między opcją jednej kości a opcją dwóch kości):

Zestawy wybrane przez przeciwników		Zwycięski zestaw kości
Zestawy wybrane przez przeciwników		Typ	Numer
A	B	mi	1
A	C	mi	2
A	D	C	2
A	mi	D	1
B	C	A	1
B	D	A	2
B	mi	D	2
C	D	B	1
C	mi	B	2
D	mi	C	1

Z tym zestawem wiążą się jednak dwa główne problemy. Pierwszym z nich jest to, że w opcji gry z dwiema kostkami pierwszy łańcuch powinien pozostać dokładnie taki sam, aby gra była nieprzechodnia. W praktyce jednak D faktycznie pokonuje C. Drugi problem polega na tym, że trzeci gracz musiałby mieć możliwość wyboru między opcją jednej kości a opcją dwóch kości – co może być postrzegane jako niesprawiedliwe w stosunku do innych graczy.

Poprawiono kości Grime'a

Powyższy problem D pokonującego C powstaje, ponieważ kości mają 6 ścian zamiast 5. Zastępując najniższą (lub najwyższą) ściankę każdej kości „przerzutem” (R), wszystkie pięć kości będzie działać dokładnie tak, jak zamierzał dr James Grime :

O: R, 2, 2, 7, 7, 7
B: R, 1, 6, 6, 6, 6
C: R, 5, 5, 5, 5, 5
D: R, 4, 4, 4, 4, 9
P: R, 3, 3, 3, 8, 8

Alternatywnie, ściany te można odwzorować na zestaw kości pięciokątno-trapezoedrycznych (10-ściennych), przy czym każda liczba pojawia się dokładnie dwa razy, lub na zestaw kości dwudziestościennych (20-ściennych), przy czym każda liczba występuje cztery razy. Eliminuje to potrzebę „przerzucania” twarzy.

Rozwiązanie to zostało odkryte przez Jona Chambersa, australijskiego nauczyciela matematyki przygotowującego do służby. ^{[ potrzebne źródło ]}

Czterech graczy

Zestaw dla czterech graczy nie został jeszcze odkryty, ale udowodniono, że taki zestaw wymagałby co najmniej 19 kości.

Nieprzechodnie 4-ścienne kości

Tetrahedra może być używana jako kostka z czterema możliwymi wynikami .

Zestaw 1

O: 1, 4, 7, 7
B: 2, 6, 6, 6
K: 3, 5, 5,8

9/16 ) = P ( B > C) = P(C > A) =

Poniższe tabele przedstawiają wszystkie możliwe wyniki:

B A	2	6	6	6
1	B	B	B	B
4	A	B	B	B
7	A	A	A	A
7	A	A	A	A

W „A kontra B” A wygrywa w 9 z 16 przypadków.

C B	3	5	5	8
2	C	C	C	C
6	B	B	B	C
6	B	B	B	C
6	B	B	B	C

W „B kontra C” B wygrywa w 9 z 16 przypadków.

A C	1	4	7	7
3	C	A	A	A
5	C	C	A	A
5	C	C	A	A
8	C	C	C	C

W „C kontra A” C wygrywa w 9 z 16 przypadków.

Zestaw 2

O: 3, 3, 3, 6
B: 2, 2, 5, 5
C: 1, 4, 4, 4

P(A > B) = P(B > C) = 10 / 16 , P(C > A) = 9/16

Nieprzechodnie kości 12-ścienne

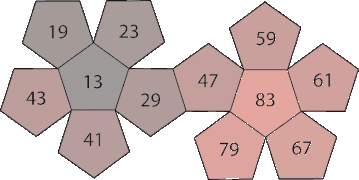
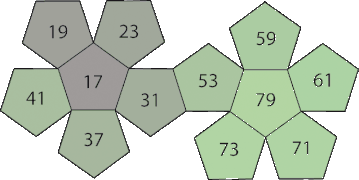
Analogicznie do nieprzechodnich kości sześciościennych istnieją również dwunastościany, które służą jako nieprzechodnie kości dwunastościenne . Suma punktów na każdej z kostek wynosi 114. Na żadnym z dwunastościanów nie ma powtarzających się liczb.

Dwunastościany Miwina (set 1) cyklicznie wygrywają ze sobą w stosunku 35:34.

Dwunastościany miwina (zestaw 2) cyklicznie wygrywają ze sobą w stosunku 71:67.

Zestaw 1:

DIII	fioletowy	1	2			5	6	7		9	10	11			14	15	16		18
DIV	czerwony	1		3	4	5			8	9	10		12	13	14			17	18
DV	ciemno szary		2	3	4		6	7	8			11	12	13		15	16	17

DIII
DIV
DV

Zestaw 2:

D VI	cyjan	1	2	3	4					9	10	11	12	13	14			17	18
VII	gruszka zielona	1	2			5	6	7	8	9	10					15	16	17	18
D VIII	jasnoszary			3	4	5	6	7	8			11	12	13	14	15	16

D VI
VII
D VIII

Nieprzechodnie 12-ścienne kości o liczbach pierwszych

Możliwe jest również konstruowanie zbiorów nieprzechodnich dwunastościanów w taki sposób, że nie ma liczb powtarzających się, a wszystkie liczby są liczbami pierwszymi. Nieprzechodnie dwunastościany Miwina o liczbach pierwszych wygrywają cyklicznie ze sobą w stosunku 35:34.

Zestaw 1: Liczby sumują się do 564.

PD 11	szary do niebieskiego	13	17	29	31	37	43	47	53	67	71	73	83
PD 12	szary do czerwonego	13	19	23	29	41	43	47	59	61	67	79	83
PD 13	szary do zielonego	17	19	23	31	37	41	53	59	61	71	73	79

PD 11
PD 12
PD 13

Zestaw 2: Liczby sumują się do 468.

PD 1	oliwkowy do niebieskiego	7	11	19	23	29	37	43	47	53	61	67	71
PD 2	turkusowy do czerwonego	7	13	17	19	31	37	41	43	59	61	67	73
PD 3	fioletowy do zielonego	11	13	17	23	29	31	41	47	53	59	71	73

PD 1
PD 2
PD 3

Zobacz też

Źródła

Gardner, Martin (2001). The Colossal Book of Mathematics: klasyczne łamigłówki, paradoksy i problemy: teoria liczb, algebra, geometria, prawdopodobieństwo, topologia, teoria gier, nieskończoność i inne tematy matematyki rekreacyjnej (wyd. 1) . Nowy Jork: WW Norton & Company. P. 286 –311. ^{[ Brak numeru ISBN ]}
Spielerische Mathematik mit Miwin'schen Würfeln (w języku niemieckim). Bildungsverlag Lemberger. ISBN 978-3-85221-531-0 .

Linki zewnętrzne