Kolumna Taylora

Ruch płynu powyżej i poniżej poruszającego się obiektu jest zmuszany do cyrkulacji, a zatem jest ograniczony do kolumny przedłużonej przez obiekt w osi obrotu.

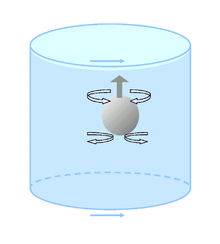
Kolumna Taylora to zjawisko dynamiki płynów, które występuje w wyniku efektu Coriolisa . Został nazwany na cześć Geoffreya Ingrama Taylora . Wirujące płyny, które są zaburzone przez ciało stałe, mają tendencję do tworzenia kolumn równoległych do osi obrotu, zwanych kolumnami Taylora.

Obiekt poruszający się równolegle do osi obrotu w obracającym się płynie doświadcza większej siły oporu niż w płynie, który się nie obraca. Na przykład silnie wyporna piłka (taka jak piłeczka do ping-ponga) unosi się na powierzchnię wolniej niż w płynie, który się nie obraca. Dzieje się tak, ponieważ płyn na ścieżce piłki, która jest wypychana z drogi, ma tendencję do krążenia z powrotem do punktu, z którego został przesunięty, z powodu efektu Coriolisa. Im większa prędkość obrotowa, tym mniejszy promień koła bezwładnościowego pokonywanego przez płyn.

Jednostka płynu (reprezentowana przez czarną kropkę) jest wypychana z powrotem do punktu, z którego została przesunięta.

W nieobracającym się płynie płyn rozdziela się nad wznoszącą się kulą i zamyka pod nią, stawiając kuli stosunkowo niewielki opór. W obracającym się płynie kula musi wypchnąć nad sobą całą kolumnę płynu i musi przeciągnąć całą kolumnę płynu pod sobą, aby wznieść się na powierzchnię.

Wirujący płyn wykazuje zatem pewien stopień sztywności.

Historia

Kolumny Taylora zostały po raz pierwszy zaobserwowane przez Williama Thomsona, Lorda Kelvina , w 1868 r. Kolumny Taylora zostały przedstawione w demonstracjach wykładowych Kelvina w 1881 r. I Johna Perry'ego w 1890 r. Zjawisko to zostało wyjaśnione za pomocą twierdzenia Taylora-Proudmana i zostało zbadane przez Taylor, Grace, Stewartson i Maxworthy — między innymi.

Teoria

Kolumna Taylora w płynie

Kolumny Taylora zostały dokładnie zbadane. Dla Re <<1, Ek <<1, Ro <<1, równania oporu walca o promieniu a , stwierdzono następującą zależność.

${\ Displaystyle F = {\ Frac {16} {3}} \ rho a ^ {3} \ Omega U}$

Aby to wyprowadzić, Moore i Saffman rozwiązali linearyzowane równanie Naviera-Stokesa we współrzędnych cylindrycznych, gdzie niektóre pionowe i promieniowe składowe członu lepkiego są uważane za małe w stosunku do składnika Coriolisa:

${\ Displaystyle -2 \ Omega v = - {\ Frac {1} {\ rho}} {\ Frac {\ częściowe p} {\ częściowe r}}}$

${\ Displaystyle 2 \ Omega u = \ nu \ lewo ({\ Frac {\ częściowe ^ {2} v} \częściowy r^{2}}}+{\frac {1}{r}}{\frac {\częściowy v}{\częściowy r}}-{\frac {v^{2}}{r}}\ Prawidłowy)}$

${\ Displaystyle 0 = - {\ Frac {1} {\ rho}} {\ Frac {\ częściowe p} {\częściowe z}}+\nu \left({\frac {\częściowe ^{2}w}{\częściowe r^{2}}}+{\frac {1}{r}}{\frac {\ częściowe w}{\częściowe r}}\prawo)}$

Aby rozwiązać te równania, uwzględniamy również warunek zachowania objętości:

${\ Displaystyle {\ Frac {1} {r}}} {\ Frac {\ częściowe (ur)}} {\ częściowe r}} + {\ Frac {\ częściowe w}{\częściowe z}}=0}$

Używamy relacji zgodności Ekmana dla tej geometrii, aby ograniczyć postać prędkości na powierzchni dysku:

${\ Displaystyle wU = \ pm {\ Frac {1} {2}} {\ sqrt {\ Frac {\ nu} {\ Omega}} }{\frac {1}{r}}{\frac {\częściowy (rv)}{\częściowy r}}}$

Wynikowe pola prędkości można rozwiązać za pomocą funkcji Bessela .

${\ Displaystyle u = - {\ Frac {\ nu} {2 \ Omega}} \int \limits _{0}^{\infty }k^{2}A(k)J_{1}(kr)e^{-\nu k^{3}z/2\Omega }dk}$

${\ Displaystyle v = \ int \ ograniczenia _ {0} ^ {\ infty} A (k) J_ {1 }(kr)e^{-\nu k^{3}z/2\Omega }dk}$

${\ Displaystyle w = - \ int \ ograniczenia _ {0} ^ {\ infty} A (k) J_ { 0}(kr)e^{-\nu k^{3}z/2\Omega }dk}$

gdzie dla Ek <<1 funkcja A(k) jest dana wzorem,

${\ Displaystyle A (k) = {\ Frac {2Ua} {\ pi}} \ lewo (\ bo ka- {\ frac {\ sin ka} {ka}} \ dobrze)}$

Całkując równanie dla v , możemy znaleźć ciśnienie, a tym samym siłę oporu określoną przez pierwsze równanie.

Dalsza lektura

• Brenner, Michael P.; Kamień, Howard A. (maj 2000). „Nowoczesna fizyka klasyczna dzięki pracom GI Taylora” . Fizyka dzisiaj . 53 (5): 30–35. Bibcode : 2000PhT....53e..30B . doi : 10.1063/1.883100 .

Linki zewnętrzne

• Kolumny Taylora (Martha Buckley, MIT)
• Dynamika płynów odtwarzacza: eksperyment z kolumną Taylora (UCLA Spin Lab)