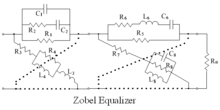
Korektory kratowe i zmostkowane-T

Korektory kratowe i zmostkowane-T to obwody używane do korygowania błędów amplitudy i/lub fazy sieci lub linii transmisyjnej. Zwykle celem jest osiągnięcie ogólnej wydajności systemu z płaską odpowiedzią amplitudową i stałym opóźnieniem w określonym zakresie częstotliwości, poprzez dodanie korektora. W przeszłości projektanci używali różnych technik do realizacji swoich obwodów korektora. Należą do nich metoda sieci komplementarnych; metoda asymptot linii prostych; przy użyciu specjalnie zbudowanego przyrządu testowego; wykorzystanie standardowych bloków konstrukcyjnych obwodów; lub za pomocą programów komputerowych. Ponadto stwierdzono, że metody prób i błędów są zaskakująco skuteczne, gdy są wykonywane przez doświadczonego projektanta.

W kanałach wideo lub audio korekcja powoduje, że przebiegi są przesyłane z mniejszą degradacją i mają ostrzejsze krawędzie przejściowe z mniejszymi przeregulowaniami (dzwonienie) niż wcześniej. W innych zastosowaniach, takich jak CATV lub multipleksowane częstotliwościowo sygnały telefoniczne, w których przesyłanych jest wiele sygnałów nośnych, celem jest wyrównanie linii transmisyjnej, aby sygnały te miały prawie taką samą amplitudę. Obwody kratowe i zmostkowane-T są preferowane w pasywnych korektorach, ponieważ można je skonfigurować jako sieci o stałej rezystancji, takie jak sieć Zobela , jak wskazał Zobel , a później Bode .

Jednowyrazowy opis „korektor” jest powszechnie używany, gdy głównym celem sieci jest korygowanie odpowiedzi amplitudowej systemu, nawet jeśli w tym samym czasie można również uzyskać pewną korzystną korekcję fazy. Gdy głównym problemem jest korekcja fazy, używany jest bardziej wyraźny termin „korektor fazy” lub „korektor fazy”. (W tym przypadku obwód jest zwykle siecią wszechprzepustową, która w ogóle nie zmienia odpowiedzi amplitudowej, na przykład korektor fazy sieci ).

Podczas wyrównywania zbalansowanej linii transmisyjnej sieć jest najlepszą konfiguracją obwodu do zastosowania, podczas gdy w przypadku obwodu z jednym końcem z płaszczyzną uziemienia bardziej odpowiednia jest sieć mostkowa. Chociaż obwody wyrównawcze, dowolnej postaci, mogą być zaprojektowane do kompensacji szerokiego zakresu charakterystyk amplitudowych i fazowych, mogą stać się bardzo skomplikowane, gdy zadanie kompensacji jest trudne, jak pokazano później.

Do projektowania korektorów wykorzystano różne metody, a niektóre z nich opisano poniżej. Kilka procedur pochodzi z początku XX wieku, kiedy szybko rozwijający się przemysł telefoniczny potrzebował korektorów. Później, wraz z pojawieniem się telewizji, bardzo ważne stało się wyrównanie łączy wideo.

Korekta amplitudy

Celem sieci korektora jest korygowanie braków w odpowiedzi amplitudowej linii transmisyjnej, sieci elementów skupionych lub łańcucha wzmacniacza. Wyrównanie jest często konieczne w przypadku linii transmisyjnych i linii opóźniających z elementami skupionymi, które mają tendencję do zwiększania strat wraz z częstotliwością. Bez korekcji wierność przebiegu jest tracona, a czasy narastania i opadania stanów przejściowych ulegają pogorszeniu (tzn. są mniej ostre). Czasami korekcja amplitudy jest wymagana z bardziej subtelnych powodów, na przykład w przypadku analogowych przebiegów telewizji kolorowej mogą wystąpić błędy kolorów w wyświetlanych obrazach, gdy odpowiedź systemu transmisji nie jest płaska. Zwykle wybiera się korektory kratowe i zmostkowane-T, które są sieci o stałym oporze . Zobel, a później Bode zwrócił uwagę, że takie sieci mogą być kaskadowane między sobą oraz z linią transmisyjną lub obwodem elementów skupionych, bez wprowadzania problemów z niedopasowaniem. Stosowanie konfiguracji ze stałą rezystancją jest powszechną praktyką w projektowaniu korektorów od wielu lat i prawie wszystkie przykłady przedstawione w tym artykule mają tę właściwość.

Bez względu na metodę projektowania, korektory pasywne zawsze wprowadzają dodatkowe tłumienie w ścieżce transmisyjnej, co musi zostać naprawione przez wzmacniacz lub repeater .

Metoda sieci komplementarnych

W niektórych swoich wczesnych pracach Zobel opracował obwód z elementami skupionymi, aby symulować zachowanie danej długiej linii przesyłowej będącej przedmiotem zainteresowania. Takie urządzenie było przydatne, ponieważ umożliwiało prowadzenie prac badawczych nad systemem transmisyjnym w wygodzie laboratorium. Co ważne, jak zauważył Zobel, po zaprojektowaniu takiej sieci zawsze można było znaleźć wykonalną sieć komplementarną, która wykazywała odpowiedź odwrotną.

Przykład

Procedurę można zilustrować prostym przykładem przedstawionym przez Zobela, który pokazano poniżej. Tutaj lewa krata ma prostą charakterystykę dolnoprzepustową, a prawa siatkę ma charakterystykę uzupełniającą. Dla tego obwodu R1*R2 = L1/C1 = L2/C2 = R0^2 gdzie R1 < 2.R0 . C2 jest dane przez ${\ Displaystyle C_ {2} = {\ Duży [} {\ Duży (} {\ Frac {R_ {0}} {R_ {1}}} {\ Duży)} ^ {2} -1 { \Duży ]}.{\frac {L_{1}}{R_{0}^{2}}}}$

Kaskada sieci dolnoprzepustowych i górnoprzepustowych

Odpowiedzi indywidualne i ogólne

Dla znormalizowanej sieci R0 = 1Ω. Wybierz R1 = 0,5 Ω i L1 = 1 H, a następnie R2 = 2 Ω, C1 = 1 F, C2 = 3 F i L2 = 3 H

Odpowiedzi poszczególnych sekcji oraz odpowiedź ogólną przedstawiono na wykresach dla sieci złożonej, podanych po prawej stronie.

₀ Ten proces kompensacji można opisać matematycznie za pomocą podstawowych równań sieciowych podanych w sieci kratowej , jak następuje. Strata transmisji znormalizowanej (R = 1) sieci o stałej rezystancji z ramionami przelotowymi Z _a i poprzecznymi ramionami Z _b wynosi

${\ Displaystyle T (p) = {\ Frac {1-z_ {a}} {1 + z_ {a}}} ={\frac {z_{b}-1}{z_{b}+1}}}$

Teraz dla obwodu dolnoprzepustowego, podanego powyżej, za jest równoległą kombinacją rezystora 0,5 Ω połączonego równolegle z cewką indukcyjną 1H.

${\ Displaystyle z_ {a} (dolnoprzepustowy) = {\ Frac {0,5 \ razy p} {0,5 + p} }={\frac {p}{1+2.p}}}$

a więc

${\ Displaystyle T (dolnoprzepustowy) = {\ Frac {1-{\frac {p}{(1+2.p}}}{1+{\frac {p}{(1+2.p)}}}}={\frac {1+p}{ 1+3.p}}}$
Następnie rozważ sekcję górnoprzepustową. Tutaj za jest równoległą kombinacją rezystora 0,5Ω połączonego równolegle z kondensatorem 3F, więc

${\ Displaystyle z_ {a} (górnoprzepustowy) = {\ Frac {0,5 \times 1/3.p}{0,5+1/3.p}}={\frac {1}{2+3.p}}}$

a więc

${\ Displaystyle T (highpass) = {\ Frac {1-1 / (2 + 3.p)} {1 + 1 / (2 + 3.p)}} = {\ Frac {1 + 3.p} 3+3.p}}={\frac {1+3.p}{3(1+p)}}}$

ogólna odpowiedź Ttot to

${\ Displaystyle T_ {tot} (p) = T (dolnoprzepustowy) \ razy T (górnoprzepustowy) = {\ Frac {1 + p} {1 + 3. p}} \ razy {\ Frac {1 + 3 .p}{3(1+p)}}={\frac {1}{3}}}$ tj. płaska odpowiedź z ogólnym zyskiem jednej trzeciej. Pokazano to na powyższym rysunku. W tym przykładzie ogólna charakterystyka jest bezfazowa, tj. oprócz korekcji amplitudy uzyskano pełną kompensację fazy. Dzieje się tak, ponieważ dokładna korekcja została osiągnięta na wszystkich częstotliwościach. Często korekcja jest skuteczna tylko w ograniczonym zakresie częstotliwości, w którym to przypadku wynik końcowy będzie zawierał pewną fazę resztkową.

Mówiąc bardziej ogólnie, odpowiedź obwodu lub linii transmisyjnej może być trudna do dokładnego odtworzenia za pomocą obwodów z elementami skupionymi, więc zwykłym zadaniem jest znalezienie możliwej do zrealizowania charakterystyki, która jest akceptowalnym dopasowaniem. Czasami metody prób na błędach, stosowane w systematyczny sposób, mogą okazać się skuteczne

Obwód korektora ogólnego przeznaczenia

Gdy ramiona sieci kratowej są czysto reaktywne, możliwe są sieci all-pass o stałej rezystancji, jak pokazano w sieci opóźniającej sieć . Jeśli jednak w ramionach sieci znajdują się rezystory, możliwe są różne odpowiedzi amplitudowe przy jednoczesnym zachowaniu właściwości stałej rezystancji.

Pokazano tutaj jeden, często używany obwód korektora, wraz z równoważnym obwodem zmostkowanym. Równoważność między kratą a mostkiem-T można pokazać za pomocą twierdzenia o bisekcji Bartletta . Obwody mają stałą charakterystykę rezystancji, gdy Z1.Z2 = R02.

Wspólny obwód korektora

Funkcja przenoszenia tego obwodu to ${\ Displaystyle T (p) = {\ Frac {R_ {0}} {R_ {0} + Z_ {1} (p) }}}$

Po znormalizowaniu tak, że źródło i rezystory końcowe oraz R0 są jednością, a Z1.Z2 = 1, staje się ${\ Displaystyle T (p) = {\ Frac {1} {1+Z_{1}(p)}}}$

więc Z1, jako funkcja T, jest dana przez ${\ Displaystyle Z_ {1} (p) = {\ Frac {1} {T (p)}} -1}$

Prostota tego równania (należy znaleźć tylko jedną impedancję) sprawia, że obwód jest popularny w projektach korektorów.

Metoda asymptot linii prostych

Metoda wykorzystuje początkową odpowiedź próbną, składającą się z sekwencji asymptot linii prostych, w celu określenia położenia bieguna/zera możliwej do zrealizowania sieci.

Ogólne zasady metody są następujące.

Pojedynczy biegun przy p = -a

Odpowiedź pojedynczego bieguna i asymptoty

Rozważmy przypadek prostego obwodu dolnoprzepustowego RC, którego funkcja przenoszenia ma jeden biegun na osi częstotliwości rzeczywistej przy p = -a, jak pokazano. Odpowiedź wynosi -3 dB przy ω = a i spada do 6 dB na oktawę przy wysokim częstotliwości. Jest pokazany na wykresie, w decybelach, w funkcji częstotliwości (w skali logarytmicznej). Po prawej stronie pokazano również dwuliniowe przybliżenie asymptotyczne, z częstotliwością przerwania również przy ω = a. Jak widać, rzeczywista odpowiedź i aproksymacja linii prostej są ściśle dopasowane w większości zakresu częstotliwości, odchylając się tylko w pobliżu ω = a.

Jeśli teraz dodamy zero przy, powiedzmy, -10×a, to wprowadzona zostanie nowa asymptota z dodatnim nachyleniem 6 dB na oktawę, zaczynając od ω = 10, jak pokazano.

Biegun i zero

Odpowiedź bieguna i zera + asymptoty

Rozszerzając metodę, skomplikowaną charakterystykę tłumienia można aproksymować za pomocą sekwencji asymptot linii prostych, pod warunkiem, że najbardziej strome nachylenie charakterystyki tłumienia nie przekracza 6 dB na oktawę w zakresie częstotliwości. Wyniki są wykreślane w skali dB w funkcji częstotliwości w skali logarytmicznej, jak poprzednio.

${\ Displaystyle T (p) = {\ Frac {(p + b) (p + d) (....} {(p + a) (p + c) (...)} \ quad gdzie \ a<b<c<d<....itp.}$ , transmitancja

Po uznaniu, że wyrażenie spełnia wymaganie z wystarczającą dokładnością, impedancje Z1 i Z2 można znaleźć na podstawie podanych wcześniej zależności.

Przykład

Na przykład strata transmisji hipotetycznej sieci dystrybucyjnej, której odpowiedź jest pokazana pełną linią na rysunku po lewej stronie, ma zostać skorygowana (wyrównana). W tym przykładzie wymagana jest korekcja w zakresie częstotliwości od Ω ₁ = 0,09 r/s do Ω ₂ = 140 r/s. Można to przybliżyć za pomocą serii prostych odcinków, jak pokazano na rysunku. Częstotliwości dobiera się tak, aby różne błędy wykazywane przez przybliżenie w linii prostej były wszystkie podobne i jak najmniejsze.

Odpowiedź + asymptotyczne ok.

Odpowiedź celu i odpowiedź sieci

Przybliżenie linii prostej pokazane na rysunku ma bieguny przy ω = 0,333 r/s i 10 r/s oraz zera przy ω = 1 r/s i 30 r/s.

Funkcja przenoszenia sieci z tymi biegunami i zerami jest dana przez

${\ Displaystyle T (p) = {\ Frac {(1 + p) (1 + 0,03333 p )}{(1+3p)(1+0,1p)}}}$

Rzeczywistą odpowiedź (wielkość) T można łatwo obliczyć i pokazano na wykresie po prawej stronie jako funkcję częstotliwości wraz z odpowiedzią docelową. Większe dopasowanie wymagałoby dodatkowych biegunów i zer w T(p) przy bliższych odstępach.

Sieć dolnoprzepustowa T(p) z tą odpowiedzią będzie miała sieć LC dla Z1 i sieć RC dla Z2, gdy zostanie zrealizowana przy użyciu opisanych wcześniej prostych obwodów. Jednak bardziej interesująca jest tutaj sieć komplementarna, ponieważ koryguje ona spadającą utratę transmisji tej odpowiedzi.

Funkcja przenoszenia sieci korektora będzie ${\ Displaystyle Te (p) = {\ Frac {1} {T (p)}} = {\ Frac {1 {K}}.{\frac {(1+3p)(1+0,1p)}{(1+p)(1+0,03333p)}}}$ gdzie K = 9, tak że zysk sieci nigdy nie przekracza jedności przy żadnej częstotliwości.

$(p) }}-1}$ p )

${\ Displaystyle Z_ {1} (p) = {\ Frac {8 + 6,2 p} {(1 + 3 p)$ )

Z1 można zrealizować jako sieć drabinkową RC (lub jako równoległą kombinację dwóch impedancji RC, z których każda jest szeregowo połączonym rezystorem i kondensatorem).

Impedancje sieciowe dla korektora

Wyrównana odpowiedź

Wersja sieci drabinkowej Z1 jest pokazana po lewej stronie, wraz z wersją Z2 (jego podwójną siecią). Wartości składowych dla Z1 (przy R0 = 1) wynoszą: C1 = 0,04838F, C2 = 0,4747F, R1 = 2,2857Ω, R2 = 5,7152Ω a dla Z2 są to L1 = 0,0438H, L2 = 0,4747H, R3 = 0,4375, R4 = 0,1750.

Te obwody Z1 i Z2 mogą być użyte bezpośrednio w sieci korektora mostkowego T, ale w sieci kratowej wartości kondensatorów powinny być podwojone, a wartości rezystorów zmniejszone o połowę w sieci Z1, a wszystkie wartości rezystorów i cewek indukcyjnych podwojone w sieci Z2 (tj. Za = Z1/2 i Zb = 2.Z2).

Ogólna reakcja, gdy korektor jest kaskadowany z oryginalną charakterystyką, jest pokazany po prawej stronie. Zgodnie z oczekiwaniami na wyniku występuje falowanie, które jest podobne do różnic między odpowiedzią początkową a jej przybliżeniem T(p).

Chociaż rozpatrywana w tym przykładzie odpowiedź przed wyrównaniem ma charakterystykę, która opada liniowo w funkcji log(ω), możliwe jest radzenie sobie z charakterystykami nieliniowymi w podobny sposób, pod warunkiem, że wykres opada monotonicznie – tj. nachylenie nie zmienia znaku, a maksymalne nachylenie jest mniejsze niż 6 dB/oktawę. W takich przypadkach można również znaleźć szereg asymptot linii prostych, które przybliżają odpowiedź, a tym samym prowadzą do możliwego do zrealizowania rozwiązania.

Korektory o znacznej złożoności można projektować metodą asymptot i uzyskiwać ogólną, skorygowaną odpowiedź z bardzo niskimi tętnieniami (<<0,1 dB).

Wyprowadzanie sieci kompensacyjnych za pomocą eksperymentalnego przyrządu pomiarowego

Eksperymentalny przyrząd testowy może być użyty do znalezienia wartości komponentów w celu znalezienia wartości obwodu dla korektora. Podstawowy układ obwodu pokazano po lewej stronie.

Schemat przyrządu do testowania korektora

Funkcja przenoszenia tego prostego obwodu, ignorująca płaską stratę, to ${\ Displaystyle T (p) = {\ Frac {R_ {0}} {(R_ {0} +2.Z_{x})}}}$

Teraz, jeśli 2.Zx = Z1, to staje się ${\ Displaystyle T (p) = {\ Frac {R_ {0}} {(R_ {0} + Z_ {1 })}}}$

Tak więc T(p) ma taką samą postać jak funkcja przenoszenia podstawowego obwodu wyrównawczego podana wcześniej z Zx identycznym z ramionami sieci „Za”. Tak więc, chociaż przyrząd testowy sam w sobie nie jest siecią o stałym oporze, zapewnia wygodną metodę eksperymentalną do określania wymaganych wartości składowych dla obwodu sieciowego lub zmostkowanego, który jest siecią o stałym oporze. Po ustaleniu wartości Zx wartości obwodu dla Z1 i jego dualnego Z2 można znaleźć w prosty sposób.

Sugerowany przyrząd testowy wykorzystujący te koncepcje pokazano po prawej stronie.

Przyrząd do testowania korektora

(i) Podstawowy obwód RC, który tworzy większość Zx, ma postać sieci drabinkowej, a nie równoległej kombinacji szeregowych par RC. Całkowity rozrzut wartości potrzebnych kondensatorów jest znacznie mniejszy w przypadku tej konfiguracji. Zwykle wystarcza sieć sześciu lub siedmiu sekcji. (ii) Rezystor bocznikowy R jest umieszczony na zaciskach wejściowych Zx, co również zmniejsza rozrzut wartości składowych. Niestety zmniejsza to również maksymalną korekcję możliwą przez pojedynczą sekcję korektora i może spowodować, że do uzyskania pełnej korekcji konieczne będzie kaskadowanie dwóch lub więcej sekcji. (iii) Szeregowy obwód rezonansowy LC jest również obecny na zaciskach Zx. Ta kombinacja jest przystosowana do rezonowania powyżej górnej częstotliwości pasma przepustowego systemu, a jej celem jest zmniejszenie płaskich strat korektora. (Jest to technika powszechnie stosowana w obwodach korektora). (iv) Zamiast znajdowania wartości składowych w celu uzyskania pożądanej odpowiedzi częstotliwościowej, alternatywnym podejściem jest optymalizacja wydajności przejściowej za pomocą przebiegów testowych (takich jak na przykład sygnały impulsowe i słupkowe). Optymalizacja wydajności transjentów w ten sposób ma szczególne zastosowanie w sytuacjach, w których ważna jest wierność kształtu fali, na przykład w telewizji. Gdy wartości obwodu są uzyskiwane w ten sposób, opis „korektor kształtu fali” jest preferowany w stosunku do „korektora odpowiedzi”

Przykład

Pokazano przykład „korektora kształtu fali” dla sekcji kabla koncentrycznego dla częstotliwości wideo. Impedancja bocznika Z2 nie jest pokazana szczegółowo. Jest to dual Z1, więc podczas gdy Z1 zawiera szeregowy obwód rezonansowy i sieć drabinkową RC, Z2 zawiera bocznikowy obwód rezonansowy i sieć drabinkową RL.

Przykład korektora kształtu fali

Wykres vout/vin (w dB) w funkcji częstotliwości dla tego obwodu, przy użyciu wartości składowych zaproponowanych w odnośniku, jest również pokazany po prawej stronie.

Utrata wtrąceniowa korektora kształtu fali

Procedura dopasowania krzywej Zobela

₀ Zobel w swoim wczesnym artykule opisał procedurę, w której kaskada prototypowych sieci o stałej rezystancji stanowiła podstawę jego korektorów. Jego metoda polegała zasadniczo na procedurze dopasowywania krzywej, a dodatek w jego artykule zawierał szereg sieci, z których można było zbudować kompletny korektor. Przydzielił udziały w ogólnej pożądanej odpowiedzi korektora do różnych członków kaskady kratowej (lub zmostkowanej). Każdy obwód sieciowy w kaskadzie został zidentyfikowany na podstawie impedancji Z _a i Z _b (gdzie Z _b = R ² /Z _a
oraz przez jego „funkcję propagacji” i „stałą tłumienia” (w efekcie kwadrat wielkości). Te parametry obrazu… są ze sobą powiązane, jak wykazał Zobel, patrz ( impedancja obrazu ). Po pierwsze, impedancję sieci Za można wyrazić jako stosunek dwóch wielomianów w (jf)

${\ Displaystyle {\ Frac {Z_ {1}} {R}} = {\ Frac {a_ {0} + a_ {1} (jf) + a_ {2} (jf ^ {2} +....} {b_{0}+b_{1}(jf)+b_{2}(jf)^{2}+....}}}$

₀₀ W tym wyrażeniu współczynniki impedancji a , b itd., z których jeden jest równy jedności, a niektóre mogą wynosić zero, są algebraicznymi kombinacjami elementów sieci. Dla dowolnego typu sieci współczynniki są ustalane przez elementy i odwrotnie.

Po drugie, można znaleźć stałą propagacji Γ

${ \Gamma }={\frac {g_{0}+g_{1}(jf)+g_{2}(jf^{2}+....}{h_{0}+h_{1}(jf) +h_{2}(jf)^{2}+....}}}$
₀₀₀₀ gdzie g , g ₁ , h itd. są funkcjami algebraicznymi a , b , itd. Z tego można wyprowadzić stałą tłumienia i wyrazić ją jako funkcję częstotliwości. (W latach dwudziestych XX wieku powszechną praktyką było wyświetlanie tłumienia jako parametru dodatniego, więc odpowiedź filtra dolnoprzepustowego była wyświetlana jako dodatnio wznosząca się krzywa ze wzrostem częstotliwości).

Dla stałej tłumienia wyrażenie ma postać:

${\ Displaystyle F = (e ^ {A}) ^ {2} = e ^ {2A} = 10 ^ {\ Frac {TU} {10}} = {\ Frac {P_ {0} + P_ {2}. f^{2}+P_{4}.f^{4}+....}{Q_{0}+Q_{2}.f^{2}+Q_{4}.f^{4}+ ....}}}$ , który jest stosunkiem dwóch wielomianów w f ² , w którym współczynniki można wyznaczyć ze znanych danych, czyli pomiarów. Zmieniając to, Zobel uzyskał „równanie liniowe tłumienia”, które obowiązuje dla wszystkich częstotliwości, a zatem:

₀₀ $_$ mając danych w wystarczających punktach danych (częstotliwościach), można rozwiązać rodzinę jednoczesnych równań, aby otrzymać wartości P , Q , P ₂ , Q ₂ itd. Na podstawie tych wyników Zobel pokazał w dodatku do swojej pracy, jak dla każdego prototypowego obwodu korektora można było wyprowadzić wartości składowe dla tej sekcji.

Przykład

Jako przykład procedura została wykorzystana przez Zobela do zaprojektowania korektora dla linii zrównoważonej o impedancji charakterystycznej 600 Ω i długości 50 mil, dla częstotliwości do 4,5 kHz. W tym wczesnym artykule Zobel używał „napier” (logarytm naturalny stosunku napięcia) i „jednostki transmisji” (logarytm do podstawy 10 stosunku mocy) zamiennie w swoich obliczeniach. Te dwie jednostki są powiązane przez 1 napier = 8,686 jednostek transmisyjnych. W połowie lat dwudziestych XX wieku jednostki te przemianowano na „neper” i „decybel” i to są jednostki używane tutaj.

Oryginalna charakterystyka tłumienia wymagająca korekty jest pokazana jako „Wykres 1” na poniższym rysunku.

Korektor linii telefonicznej Zobel

Zobel zaproponował, że zadowalającą wyrównaną odpowiedź można uzyskać przez kaskadę dwóch sieci typu pokazanego na rysunku po lewej stronie. Krata po lewej stronie na rysunku zapewniała korekcję odpowiedzi przy niskich częstotliwościach, a krata po prawej zapewniała korekcję przy wysokich częstotliwościach.

Biorąc pod uwagę najpierw obwód po lewej stronie, ma to liniowe równanie tłumienia

₀₀ ${\ Displaystyle P_ {0} + f ^ {2}. P_ {2} -FQ_ {0} -f ^ {2}. Q_ {2} = f ^ { 4}(F-1)}$ , więc są cztery niewiadome do znalezienia, P , P ₂ , Q , Q ₂ , więc potrzebne są dane na czterech częstotliwościach. Na podstawie danych zmierzonych w linii transmisyjnej Zobel zaproponował następujące wartości tłumienia. o godz ₁ = 40 Hz, A1 ₌ 0,536 nepera; przy f2 ₌ 200 Hz, A2 ₌ 0,291 neper; przy _f3 = 800 Hz, A3 ₌ 0,176 neper; przy f ₄ = 2000 Hz, A ₄ = 0,100 neper. (Dają one odpowiedź, która jest odwrotnością pierwotnego wykresu, zgodnie z wymaganiami korektora, ale z dowolnym przesunięciem 0,1 nepera przy najwyższej częstotliwości).

₀₀ Rozwiązanie czterech jednoczesnych równań wyprowadzonych z tych danych dało P = 102,007 × 10 ⁹ , Q = 32,20010 × 10 ⁹ , P ₂ = 5,06037 × 10 ⁶ , Q ₂ = 3,43087 × 10 ⁶ , z czego dane projektowe Zobela dały następującą składową wartości: C1 ₌ 1,2042 μF, R ₁ = 168,32 Ω, C ₂ = 4,0342 μF, R ₂ = 124,19 Ω R ₃ = 2138,72 Ω, L ₃ = 0,43351 H, R4 ₄ = 2898,55 Ω, L ₄ = 1,4523H

₀₀ W przypadku prawej sieci wybranej przez Zobela stała tłumienia ma taką samą wartość przy niskich i wysokich częstotliwościach, więc P = F i ma szczyt odpowiedzi w pobliżu częstotliwości rezonansowej C ₆ i L ₆ . Równanie liniowe tłumienia dla tej sieci to

${\ Displaystyle -P_ {2} + FQ_ {2} -f ^ {2} (F_ {0} -F) Q_{4}=(F_{0}-F)/f^{2}}$

₀₀₀₀₀₀ Wyrażenie na stałą tłumienia prawej sieci ma P = F , Q = 1 i P ₄ = F . Q ₄ , więc potrzebne były dane do rozwiązania dla P , P ₂ , Q ₂ i Q ₄ . Wykorzystano dane: przy f = 0 Hz, A1 ₌ 0,796 neper; przy f1 ₌ 3000 Hz, A1 ₌ 0,747 nepera; przy f2 ₌ 4000 Hz, A2 ₌ 0,530 neper; przy f ₃ = 4500 Hz, A ₃₀₀ = 0,300 neperów. Rozwiązanie czterech jednoczesnych równań wyprowadzonych z tych danych dało F = P = 4,913; P2 _-46,207 × ^10-8 ; Q2 = -90092× ^10-8 ; Q4 = 23,198× ^10-16 . Korzystając z tych danych, równania projektowe Zobela dla tej sieci dały następujące wartości składowych: R ₅ = 226,95 Ω, R ₆ = 143,4 Ω, L ₆ = 0,04935 H, C ₆ = 0,02476 μF R ₇ = 1586,25 Ω, R ₈ = 2510,46 Ω , L8 ₌ 8,8992mH, C ₈ = 0,137 μF

Ostateczne wyniki przedstawiono na poniższym rysunku. Wykres 1 rysunku przedstawia początkową reakcję przebiegu kabla, który miał zostać skorygowany. Kompensacja osiągnięta przez samą siatkę po lewej stronie (niskiej częstotliwości) jest pokazana na wykresie 2. Wreszcie, całkowita kompensacja jest pokazana na wykresie 3, gdy uwzględniona jest również siatka po prawej stronie.

Metoda Bodego dla wyrównania

Tematowi korektorów Bode poświęcił XII rozdział swojej znanej książki. Zwrócił uwagę, że wszystkie funkcje transferu można utworzyć z kaskady sieci o stałym oporze pierwszego i drugiego rzędu, która oczywiście obejmuje sieci korektorów. Aby pomóc w procesie projektowania sieci, Bode dostarczył szczegóły projektu czterech sieci pierwszego i czterech drugiego rzędu, aby objąć różne możliwe lokalizacje biegunów i zer w złożonej płaszczyźnie częstotliwości. Niestety, niektóre z zaproponowanych przez niego obwodów (kiedy bieguny i zera były złożone) zostały wyprowadzone przy użyciu metody syntezy Brune'a, która czasami wytwarzała impedancje sieci zawierające wzajemnie sprzężone cewki. Jednak późniejszy artykuł przedstawia alternatywne sieci, aby uniknąć tego problemu.

Przykład

Jako przykład metody rozważ realizację prostej odpowiedzi korektora podanej wcześniej. Można to zrealizować za pomocą prostych krat w układzie kaskadowym. Wymagana odpowiedź to

${\ Displaystyle Te (p) = {\ Frac {1} {T (p)}} = {\ Frac {1} {9}}.{\frac {(1+3p)(1+0,1p)}{(1+p)(1+0,03333p}}}$ Można to przepisać w ten sposób

${\ Displaystyle Te (p) = {\ Frac {(p + 0,3333 p)} {(1 + p)}}. {\ Frac {(p + 10)} {( p+30)}}}$ Można to podzielić na dwie sieci pierwszego rzędu w kaskadzie, używając obwodów typu IV z wykresu Bode'a, aby uzyskać pokazany obwód.

Korektor Bode (krata)

Korektor Bode (zmostkowany-T)

Można to łatwo przekształcić w kaskadę standardowych przekrojów T zmostkowanych o stałej rezystancji w postaci opisanej wcześniej, jak pokazano po prawej stronie. (Możliwy jest również prostszy obwód, który wykorzystuje mniej rezystorów).

Opracowanie korektora poprzez udoskonalenie obwodu

Oprócz metod opisanych wcześniej, końcowy obwód korektora można uzyskać zaczynając od prostego początkowego rozwiązania, a następnie stosując proces udoskonalania obwodu w celu zwiększenia złożoności obwodu i jego odpowiedzi, aż do uzyskania zadowalającej wydajności. Przykład otrzymanej w ten sposób sieci produkowanej komercyjnie pokazano poniżej. Ten korektor był w stanie skorygować straty w różnych długościach kabla koncentrycznego typu BICC T3205 (komercyjny wysokiej jakości kabel wideo 75 Ω). Korektor był obwodem zmostkowanym, a nie kratą, jak było to właściwe dla kabla koncentrycznego. Wyprodukowano dwie wersje obwodu, jedną dla kabli o długości od 0 do 100 stóp, a drugą dla kabli o długości od 100 do 180 stóp. Rezystory R ₁₇ i R ₁₈ zostały „dopasowane podczas testu” (z R ₁₇ × R ₁₈ = 75 ² ), aby uzyskać optymalne wyniki dla danej długości kabla.

Procedury iteracyjne za pomocą programowania komputerowego

Wraz z pojawieniem się nowoczesnych komputerów można uruchamiać złożone procedury iteracyjne, które wcześniej były zbyt czasochłonne. Możliwe są procedury, które minimalizują różnice między przybliżonym rozwiązaniem próbnym a specyfikacją docelową, albo w sensie „najmniejszych kwadratów”, albo „Czebyszewa”. Programy wykorzystują procedury iteracyjne do sukcesywnego rozwiązywania problemów programowania liniowego, wyprowadzonych lokalnie, jako sposób radzenia sobie z problemami nieliniowymi.

Przykład

Przykład ilustrujący metodę, uwzględniający charakterystykę tłumienia wtrąceniowego pokazaną na „Wykresie tłumienia” poniżej.

Wykres tłumienia dla metody iteracyjnej

Korektor do korygowania wykresu tłumienia

Wybrano kaskadę trzech sekcji sieci, jak pokazano, w celu uzyskania wymaganej odpowiedzi korektora.

Wartości składowych, otrzymane za pomocą procedury iteracyjnej, dały odpowiedź, która odpowiadała charakterystyce w sensie Czebyszewa, zgodnie z wymaganiami. Końcowy wynik był zgodny z docelową odpowiedzią na dziewięciu częstotliwościach (w obwodzie jest dziewięć stopni swobody w obwodzie R1 do R3, C1 do C3 i L1 do L3) z błędami szczytowymi wynoszącymi zaledwie ± 0,03 dB przy częstotliwościach pośrednich.

Resztkowy błąd amplitudy

Zmienne korektory

W przypadku korektorów zmiennych, które są ustawiane tylko przez zmianę wartości rezystorów, zwykle używa się tylko sieci Bridged-T, ponieważ jest mniej elementów do dopasowania niż w sieci. Nawet wtedy, aby zapewnić w pełni dopasowaną sieć, konieczne są podwójne potencjometry. Zmienne korektory są również omawiane przez Rounds i in. i Bodego. Bode był zainteresowany zmiennymi korektorami regulowanymi za pomocą jednego potencjometru, więc jego zmienne korektory nie były sieciami o stałym oporze.

Korektory fazowe

Wstęp

Korektor fazy to obwód, który jest połączony kaskadowo z siecią, aby ogólna odpowiedź fazowa była bardziej liniowa (lub aby opóźnienie grupowe było bardziej stałe). Połączony obwód będzie transmitować przebiegi z lepszą wiernością w porównaniu z wydajnością samej początkowej sieci.

Wyrównywanie faz jest często konieczne, ponieważ wiele obwodów jest zaprojektowanych w celu uzyskania określonej charakterystyki tłumienia, przy niewielkim uwzględnieniu wynikającej z tego charakterystyki fazowej. Często ma to miejsce na przykład w przypadku filtrów, w których w dążeniu do określonego wymogu selektywności nie zwraca się uwagi na odpowiedź fazową powstałej sieci (jak w przypadku procedury projektowania filtrów Cauera). Zwykle wytwarzany obwód jest fazą minimalną sieć, w której nagłe zmiany odpowiedzi amplitudowej zawsze skutkują nieliniowością odpowiedzi fazowej, ze względu na dokładny związek między amplitudą a fazą. Na przykład filtr dolnoprzepustowy o ostrej minimalnej fazie z szybkim przejściem z pasma przepustowego do pasma zaporowego zawsze będzie miał charakterystykę fazową, która znacznie odbiega od liniowej przy częstotliwościach w pobliżu częstotliwości odcięcia. Im ostrzejsze przejście, tym większe będzie to odchylenie. (Wykres opóźnienia grupowego pokaże również duży wzrost opóźnienia w tym samym obszarze częstotliwości).

Podobnie, każdemu tętnieniu amplitudy w paśmie filtru będzie towarzyszyć tętnienie charakterystyki fazowej. W wielu przypadkach zarówno tętnienia amplitudy, jak i fazy są niepożądane, dlatego nie ma sensu korygowanie jednego rodzaju tętnień bez jednoczesnego zajmowania się drugim

Jeśli wierność kształtu fali jest ważna, to nieliniowa charakterystyka fazowa jest niepożądana. Na przykład w telewizji wady obrazu, które można przypisać zniekształceniom fazowym, to nadmierne dzwonienie informacji o luminancji oraz rozmyte i fałszywe krawędzie kolorów przy przejściach informacji o kolorze.

W praktyce procedury korekcji fazy są najbardziej skuteczne, gdy są stosowane w systemach o ograniczonym paśmie, takich jak te zawierające filtr dolnoprzepustowy lub pasmowoprzepustowy. Dzieje się tak, ponieważ takie filtry z natury definiują skończone pasmo częstotliwości, w którym konieczne jest zastosowanie korekcji.

Jak pokazano w sieci kratowej , obwód kratowy all-pass jest odpowiedni jako sieć z korekcją fazy, ponieważ jest w stanie modyfikować charakterystykę fazową sieci filtrów bez wprowadzania zmian w jej odpowiedzi amplitudowej. Ponadto właściwość stałej rezystancji oznacza, że nie tworzy fałszywych odbić z powodu efektów niedopasowania, gdy jest kaskadowana z innymi sieciami.

Przykład

Jako przykład procesu korekcji fazy rozważ konwencjonalny filtr dolnoprzepustowy Butterwortha dziewiątego rzędu. Obwód pokazany poniżej jest znormalizowanym filtrem, który ma być zakończony 1 omem i częstotliwością odcięcia jedności).

Filtr Butterwortha dziewiątego rzędu

Charakterystykę amplitudową i fazową tego filtra przedstawiono na poniższych rysunkach. Na wykresie po lewej stronie pokazano również krzywą błędu fazy dla filtra (tj. odchylenie nachylenia fazy od liniowego). Jak widać na wykresie po prawej stronie, nachylenie fazy samego filtra dolnoprzepustowego jest liniowe przy niskich częstotliwościach, ale zwiększa się zbyt szybko przy wyższych częstotliwościach, ostatecznie powodując odchylenie fazy od liniowego o 100 stopni w pobliżu szczytu pasma. pasmo przepustowe.

Wykresy odpowiedzi amplitudy i błędu fazy

Reakcje fazowe

Korektor fazy dla filtra LP z n=9

Aby skorygować to odchylenie fazy, korektor fazy potrzebuje liniowej charakterystyki fazowej przy niskich częstotliwościach, ale aby asymptota liniowa była dodatnia wraz ze wzrostem częstotliwości. Kaskada trzech sieci wszechprzepustowych drugiego rzędu da wymaganą charakterystykę fazową filtra, a ich odpowiedź fazowa jest pokazana na wykresie po prawej stronie. W tym przykładzie, ponieważ filtr ma postać niezrównoważoną, konieczne jest użycie równoważników zmostkowanych T w korektorze fazy, a nie w obwodach sieciowych. Korektor fazy pokazano poniżej. Ponieważ korektor fazy jest obwodem wszechprzepustowym i o stałej rezystancji, nie zmienia odpowiedzi amplitudowej filtra.

Połączona charakterystyka ma krzywą fazową, która jest liniowa w całym paśmie przepustowym filtra, ale wynikające z tego wysokie nachylenie fazy oznacza, że kombinacja ma znacznie większe opóźnienie transmisji niż sam filtr.

W tym przykładzie filtr dolnoprzepustowy Butterwortha ma dziewięć biegunów, rozmieszczonych w równych odstępach kątowych na półkolu jedności w lewej połowie płaszczyzny częstotliwości zespolonej, a bieguny i zera każdego z trzech korektorów fazy wynoszą ± 0,866 ±0,5j.

Przejściowe reakcje

Przejściowe zachowanie filtra, gdy jest poddawany działaniu fali krokowej, pokazano powyżej. Pierwszy wykres dotyczy samego filtra, bez korekcji fazy, a drugi wykres pokazuje działanie po korekcji. Zgodnie z oczekiwaniami korekcja fazy poprawia symetrię kształtu fali, skraca czas narastania o 10–90% i z grubsza zmniejsza o połowę szczytową amplitudę przeregulowań, ale zwiększa opóźnienie.

Przegląd metod projektowania korektorów fazy

W praktyce przy projektowaniu korektorów fazy stosowano różne techniki. Najprostsza metoda wykorzystuje procedury prób i błędów, wspomagane przez podstawowe zrozumienie charakterystyki fazowej całego przejścia. Procedura może być zaskakująco skuteczna, ponieważ często wystarcza kaskada kilku korektorów fazy opartych na maksymalnie płaskiej sieci drugiego rzędu

Podobne podejście, oparte na wykorzystaniu standardowych tablic fazowych dla korektorów z opóźnieniem parabolicznym, pozwala projektantowi na określenie odpowiedniej sieci, aby spełnić dane opóźnienie szczytowe

Ulepszona procedura, zwracając uwagę, że charakterystyki opóźnienia grupowego wielu sieci można uznać za sumy wkładów parabolicznych i liniowych, wykorzystywała wykresy i wykresy w połączeniu z trzema technikami dopasowywania, a mianowicie dopasowaniem 3-punktowym, dopasowaniem nachylenia lub dopasowaniem „uśrednionym” , aby określić wartości komponentów.

Mózg opisał korekcję fazy kaskady 16 lamp próżniowych połączonych ze sobą maksymalnie płaskimi sieciami międzystopniowymi drugiego rzędu. Charakterystykę fazową wyprowadzono z pomiarów odpowiedzi amplitudowej, wykorzystując zależność między amplitudą a fazą dla sieci o minimalnym przesunięciu fazowym. Korekta fazy została dokonana przez trzy identyczne korektory fazy drugiego rzędu w postaci mostkowych sieci T.

Fredendhall podał wzór bieguna zerowego i schemat obwodu dla czterosekcyjnego korektora opóźnienia, który zaproponował FCC, aby był używany w nadajnikach w celu skompensowania charakterystyk „przeciętnego” odbiornika.

Opisano bardziej matematyczne podejście, które rozpoczyna się od wybrania podstawowej kaskady korektorów fazy, a następnie optymalizacji ich charakterystyki za pomocą prostej procedury dopasowywania krzywych. Tą metodą zaprojektowano LPF do użytku telewizyjnego.

Jeszcze bardziej wyrafinowana, iteracyjna procedura konwergencji została uruchomiona na komputerze w celu optymalizacji kaskady sekcji korekcji fazy. Dysponując wystarczającą liczbą przekrojów, aby uzyskać odpowiednią liczbę stopni swobody, można uzyskać pożądaną charakterystykę fazową w sensie Czebyszewa.

Inną procedurę optymalizacji rozpoczęto od zauważenia, że opóźnienia sekcji all-pass pierwszego i drugiego rzędu sumują się liniowo. Tak więc dla kaskady sieci M pierwszego rzędu i N drugiego rzędu można znaleźć najlepiej dopasowany wybór M i N, aby spełnić dowolną daną charakterystykę w akceptowalnych granicach, stosując procedurę aproksymacji minimax. Proces przebiegał w dwóch krokach, pierwszy polegał na znalezieniu przybliżenia, które zbiegło się z pożądanym opóźnieniem w określonym zestawie punktów. Drugi krok polegał na zaburzeniu tych punktów w celu znalezienia rozwiązania równej fali. Zwiększając liczbę sekcji, wybraną na początku, można zmniejszyć błąd tętnienia szczytowo-szczytowego tak mały, jak jest to wymagane.

Szentirmai wydał pakiet do projektowania wspomaganego komputerowo o nazwie „S/FILSYN”, który umożliwia syntezę ogólnego przeznaczenia, w tym obwody do wyrównywania amplitudy i fazy realizowane jako sieci kratowe lub mostkowe. Dokonał również przeglądu wielu innych pakietów projektowania wspomaganego komputerowo

Zobacz też