Sieć kratowa

Sieć symetryczna to dwuportowy filtr fali elektrycznej , w którym występują ukośnie skrzyżowane elementy bocznikowe – konfiguracja, która odróżnia ją od sieci drabinkowych . Układ elementów sieci pokazano na poniższym schemacie. Właściwości filtra tego obwodu zostały najpierw opracowane przy użyciu impedancji obrazu , ale później zastosowano do niego bardziej ogólne techniki analizy sieci .

sieci kratowej występuje powielanie elementów, ponieważ „impedancje szeregowe” (przykłady Za ₎ i „impedancje bocznikowe” (przykłady Zb ) występują dwukrotnie, co zapewnia projektantowi obwodów większą elastyczność dzięki _{różnorodności} możliwych do osiągnięcia odpowiedzi. Sieć kratowa może mieć charakterystykę: sieci opóźniającej, sieci korygującej amplitudę lub fazę, sieci dyspersyjnej lub jako liniowy filtr fazowy, w zależności od doboru elementów składowych elementów sieci.

Konfiguracja

Podstawową konfigurację sieci symetrycznej pokazano na schemacie po lewej stronie. Powszechnie używana wersja skrócona jest pokazana po prawej stronie, z przerywanymi liniami wskazującymi obecność drugiej pary pasujących impedancji.

W przypadku tego obwodu możliwe jest określenie impedancji charakterystycznej niezależnie od jego właściwości transmisyjnych, co jest cechą niedostępną dla struktur filtrów drabinkowych. Ponadto możliwe jest zaprojektowanie obwodu jako sieci o stałej rezystancji dla zakresu charakterystyk obwodu.

Strukturę kratową można przekształcić w postać niezrównoważoną (patrz poniżej), w celu wstawienia w obwody z płaszczyzną uziemienia. Takie konwersje zmniejszają również liczbę komponentów i rozluźniają tolerancje komponentów.

Możliwe jest przerysowanie sieci w konfiguracji mostka Wheatstone'a (jak pokazano w artykule Sieć Zobela ). Nie jest to jednak wygodny format do badania właściwości filtrów sieciowych, zwłaszcza ich zachowania w kaskadzie.

Podstawowe właściwości

Wyniki z teorii obrazu

Teoria filtrów została początkowo opracowana na podstawie wcześniejszych badań linii przesyłowych. W tej teorii przekrój filtra jest określany w kategoriach jego stałej propagacji i impedancji obrazu (lub impedancji charakterystycznej).

W szczególności dla sieci krystalicznej funkcja propagacji $γ$ i impedancja charakterystyczna $Z 0$ są określone przez:

{\ Displaystyle \ gamma = \ ln \ lewo [{\ Frac {\ sqrt {{\ Frac {Z_ {a}} {Z_ {b}}} + 1}} {\ sqrt {{\ frac {Z_ {a} }{Z_{b}}}-1}}}\right]=2\tanh ^{-1}\left({\sqrt {\frac {Z_{a}}{Z_{b}}}}\right )\qquad {\text{i}}\qquad Z_{0}={\sqrt {Z_{a}Z_{b}}}}

Po wybraniu $γ$ i $Z można znaleźć rozwiązania dla 0$ ${\ textstyle {\ frac {Z_ {a}} {Z_ {b}}}}$ i $Z za \times Z b$ , z których charakterystyka $Z a$ i $Zb każdy$ może być określony. (W praktyce wybory dla $γ$ i $Z 0$ są ograniczone do tych, które skutkują fizycznie osiągalnymi impedancjami dla $Z a$ i $Z b$ ). Chociaż obwód filtra może mieć jedno lub więcej pasm przepustowych i prawdopodobnie kilka pasm zaporowych (lub obszarów tłumienia), tutaj rozważane są tylko sieci z jednym pasmem przepustowym.

W paśmie przepustowym obwodu iloczyn $Z a \times Z b$ jest rzeczywisty (tzn. $Z 0$ jest rezystancyjny) i może być przyrównany do $R 0$ , końcowej rezystancji filtra. Więc

{\ Displaystyle Z_ {a} Z_ {b} = R_ {0} ^ {2} \ qquad {\ tekst {lub} }\qquad {\frac {Z_{a}}{R_{0}}}={\frac {R_{0}}{Z_{b}}}\qquad {\text{(dla częstotliwości w paśmie przepustowym)} }}

Oznacza to, że w tym zakresie częstotliwości impedancje zachowują się jak dublety względem siebie.

W zakresie tłumienia filtra charakterystyczna impedancja filtra jest czysto urojona i

{\ Displaystyle Z_ {a} = Z_ {b} \ qquad \ qquad \ qquad {\ tekst {(dla częstotliwości w paśmie tłumienia)}}}

W konsekwencji, w celu uzyskania określonej charakterystyki, reaktancje w obrębie $Za .$ i $Zb zaporowym$ dobiera się tak, aby ich częstotliwości rezonansowe i antyrezonansowe były podwójne względem siebie w paśmie przepustowym i dopasowane do siebie w paśmie Obszar przejściowy filtru, w którym następuje zmiana z jednego zestawu warunków na inny, można zawęzić tak, jak jest to wymagane, zwiększając złożoność $Z a$ i $Z b$ . Odpowiedź fazowa filtra w paśmie przepustowym jest regulowana przez lokalizacje ( odstępy) $Za częstotliwości$ rezonansowych i antyrezonansowych i $Zb .$

Dla wygody znormalizowane parametry $y 0$ i $Z 0$ są zdefiniowane przez

{\ Displaystyle y_ {0} = {\ sqrt {\ Frac {Z_ {b}} {Z_ {a}}}} = {\ sqrt {\frac {z_{b}}{z_{a}}}}\qquad {\text{i}}\qquad z_{0}={\sqrt {z_{a}z_{b}}}}

wprowadzono znormalizowane wartości $z a = Z a / R 0$ oraz $z b = Z b / R. 0$ Parametr $y 0$ jest nazywany funkcją indeksu, a $Z 0$ impedancją charakterystyczną znormalizowanej sieci. Parametry $y 0$ i $Z 0$ zbliżają się do jedności odpowiednio w obszarach tłumienia i transmisji.

Kaskada krat

Wszystkie sieci kratowe wysokiego rzędu można zastąpić kaskadą prostszych sieci, pod warunkiem, że wszystkie ich impedancje charakterystyczne są równe impedancjom oryginału, a suma ich funkcji propagacji jest równa oryginałowi.

W szczególnym przypadku sieci wszechprzepustowych (sieci, które modyfikują tylko charakterystykę fazową), dowolną daną sieć można zawsze zastąpić kaskadą sieci drugiego rzędu wraz z ewentualnie jedną siecią pierwszego rzędu.

Niezależnie od rozważanych wymagań dotyczących filtrów, proces redukcji skutkuje prostszą strukturą filtrów, z mniej rygorystycznymi wymaganiami dotyczącymi tolerancji komponentów.

Wady teorii obrazu

Charakterystyka filtra przewidywana przez teorię obrazu wymaga prawidłowo zakończonej sieci. Ponieważ niezbędne zakończenia są często niemożliwe do osiągnięcia, jako zakończenia powszechnie stosuje się rezystory, co skutkuje niedopasowaniem filtra. W konsekwencji przewidywane odpowiedzi amplitudowe i fazowe obwodu nie będą już zgodne z przewidywaniami teorii obrazu. Na przykład w przypadku filtra dolnoprzepustowego, gdzie niedopasowanie jest największe w pobliżu częstotliwości odcięcia, przejście z pasma przepustowego do pasma zatrzymania jest znacznie mniej ostre niż oczekiwano.

Poniższy rysunek ilustruje problem. Filtr siatkowy, równoważny dwóm sekcjom filtra dolnoprzepustowego o stałym k, został wyprowadzony metodami obrazowymi. (Sieć jest znormalizowana, gdzie $L = 1$ i $C = 1$ , więc $0 R = \sqrt L / C = 1$ i $ω c = 2 \sqrt L C = 2$ . Rysunek po lewej stronie przedstawia obwód sieci, a rysunek po prawej stronie daje strata wtrąceniowa z siecią zakończoną (1) rezystancyjnie i (2) z prawidłową impedancją charakterystyczną.

Two section filter with resistive terminations.png

Aby zminimalizować problem niedopasowania, Otto Julius Zobel i inni zaproponowali różne formy zakończeń filtrów obrazu , ale nieuniknione kompromisy doprowadziły do tego, że metoda wypadła z łask. Została ona zastąpiona bardziej dokładnymi metodami analizy i syntezy sieci .

Wyniki uzyskane na podstawie analizy sieci

Ten schemat pokazuje ogólny obwód sieci symetrycznej:

Dzięki analizie siatki lub analizie węzłów obwodu można znaleźć jego pełną funkcję przenoszenia. To jest,

{\ Displaystyle {\ Frac {v_ { \text{out}}}{v_{\text{in}}}}={\frac {Z_{L}(Z_{b}-Z_{a})}{(Z_{a}+Z_{b} )(Z_{S}+Z_{L})+2(Z_{a}Z_{b}+Z_{S}Z_{L})}}}

Impedancje wejściowa i wyjściowa ( $Z in$ i $Z out$ ) sieci są podane przez

{\ Displaystyle {\ rozpocząć {wyrównane} Z _ {\ tekst {w}} = {\ Frac {2Z_ {a} Z_ {b} + Z_ {L} (Z_ {a} + Z_ {b})} {Z_ {a}+Z_{b}+2Z_{L}}}\\[1ex]Z_{\text{out}}={\frac {2Z_{a}Z_{b}+Z_{S}(Z_{a }+Z_{b})}{Z_{a}+Z_{b}+2Z_{S}}}\end{wyrównane}}}

Te równania są dokładne dla wszystkich możliwych do zrealizowania wartości impedancji, w przeciwieństwie do teorii obrazu, w której funkcja propagacji dokładnie przewiduje wydajność tylko wtedy, gdy $Z S$ i $Z L$ są dopasowanymi impedancjami charakterystycznymi sieci.

Równania można uprościć, przyjmując szereg założeń. Po pierwsze, sieci są często zasilane i kończone przez rezystory o tej samej wartości $R 0$ , tak że $Z S = Z L = R 0$ , a równania stają się

{\ Displaystyle {\ rozpocząć {wyrównane}} {\ Frac {v _ {\ tekst {na zewnątrz}}} {v_ {\ tekst {w}}}} & = {\ Frac {R_ {0} (Z_ {b} - Z_{a})}{2(Z_{a}+R_{0})(Z_{b}+R_{0})}}\\[1ex]Z_{\text{in}}=Z_{\text {out}}&={\frac {2Z_{a}\,Z_{b}+R_{0}(Z_{a}+Z_{b})}{Z_{a}+Z_{b}+2R_{ 0}}}\end{wyrównane}}}

Po drugie, jeżeli impedancje $Za uproszczenie$ i $Zb :$ są wzajemnie dualne, tak że $0 Z a Z b = R 2$ , możliwe jest dalsze

{\ Displaystyle {\ Frac {v _ {\ text {out} }}{v_{\text{w}}}}={\frac {R_{0}-Z_{a}}{2(R_{0}+Z_{a})}}={\frac {Z_{ b}-R_{0}}{2(R_{0}+Z_{b})}}\qquad {\text{i}}\qquad Z_{\text{in}}=Z_{\text{out} }=R_{0}}

więc takie sieci są sieciami o stałym oporze.

Wreszcie, dla sieci znormalizowanych, gdzie $0 R = 1$ ,

{\ Displaystyle {\ Frac {v_ {\ text{out}}}{v_{\text{in}}}}={\frac {(1-z_{a})}{2(1+z_{a})}}={\frac {(z_ {b}-1)}{2(1+z_{b})}}\qquad \qquad {\text{and}}\qquad z_{\text{in}}=z_{\text{out}}= 1}

Jeżeli impedancje $Z a$ i $Z b$ (lub znormalizowane impedancje $z a$ i $z b$ ) są czystymi reaktancjami, to sieci stają się wszechprzepustowe, o stałej rezystancji, z płaską charakterystyką częstotliwościową, ale zmienną odpowiedzią fazową. To czyni je idealnymi jako sieci opóźniające i korektory fazy.

Gdy rezystory są obecne w $Z a$ i $Z b$ , wtedy, pod warunkiem, że warunek dualności nadal ma zastosowanie, obwód będzie miał stałą rezystancję, ale będzie miał zmienną odpowiedź amplitudową. Jednym z zastosowań takich obwodów są korektory amplitudy.

Konwersje i równoważności

(Zobacz referencje)

T do siatki

Pi do kraty

Wspólny element serii

Wspólny element równoległy

Połączenie dwóch krat w jedną

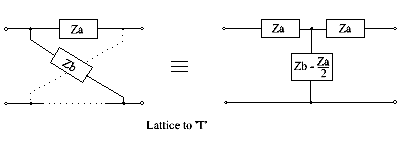
Krata do T (patrz także następna sekcja)

Shunt element of Tee should be .5*(Zb-Za), Not Zb-Za/2

Ta konwersja sieci na T daje możliwy do zrealizowania obwód tylko wtedy, gdy ocena $(Z b - Z a) / 2$ daje składowe o wartościach dodatnich. W innych sytuacjach mostek-T może zapewnić rozwiązanie, jak omówiono w następnej sekcji.

Niezrównoważone odpowiedniki

Krata jest zrównoważoną konfiguracją, która nie nadaje się do niektórych zastosowań. W takich przypadkach konieczne jest przekształcenie obwodu w elektrycznie równoważną postać niezrównoważoną. Zapewnia to korzyści, w tym zmniejszoną liczbę komponentów i złagodzone tolerancje obwodów. Prostą procedurę konwersji przedstawioną w poprzedniej sekcji można zastosować tylko w ograniczonym zbiorze warunków - generalnie konieczna jest jakaś forma zmostkowanego obwodu T. Wiele konwersji wymaga włączenia idealnego transformatora 1:1, ale istnieją konfiguracje, które pozwalają uniknąć tego wymogu, a jeden przykład pokazano poniżej.

Ta procedura konwersji rozpoczyna się od wykorzystania właściwości sieci, w której wspólny element serii we wszystkich ramionach można wyjąć poza sieć jako dwa elementy serii (jak pokazano powyżej). Wielokrotne stosowanie tej właściwości umożliwia wyodrębnianie składników ze struktury sieci. Wreszcie, za pomocą twierdzenia o bisekcji Bartletta , uzyskuje się niezrównoważony mostkowy obwód T.

Na rysunku po lewej stronie ramię Za _ma kondensator bocznikowy C _a , a ramię Zb _ma kondensator szeregowy _Cb . W konsekwencji Z _a składa się z C _a równolegle z Z _a ′, a Z _b składa się z C _b szeregowo z Z _b ′. Można to rozwinąć w pokazany niezrównoważony mostek T, pod warunkiem, że $C a > C b$ .

(Alternatywna wersja tego obwodu ma konfigurację T kondensatorów zastąpioną układem Pi (lub Delta). Dla tej konwersji T na Pi, patrz równania w Tłumik (elektronika) ).

Gdy $Cb . > C a$ , konieczna jest alternatywna procedura, w której najpierw wyciąga się wspólne cewki indukcyjne z ramion sieci Jak pokazano, cewka indukcyjna La _bocznikuje Z _{a ′} , a cewka indukcyjna Lb jest _połączona szeregowo z Zb _′ . Prowadzi to do alternatywnego zmostkowanego obwodu T po prawej stronie.

Jeżeli $L a > L b$ , to cewkę o wartości ujemnej można uzyskać za pomocą wzajemnie sprzężonych cewek. Aby osiągnąć ujemną indukcyjność wzajemną, dwie sprzężone cewki indukcyjne L1 i L2 są uzwojone „wspomagając szeregowo”.

Equivalent for Mutually Coupled Coils.png

Tak więc w końcu obwód zmostkowany-T przybiera formę

Obwody z mostkiem typu T, takie jak te, mogą być używane w sieciach opóźniających i korygujących fazę.

Inna konfiguracja sieci, zawierająca rezystory, jest pokazana poniżej. Ma rezystory bocznikujące Ro na Z _a i rezystory szeregowe Ro jako część Z _b , jak pokazano na rysunku po lewej stronie. Można go łatwo przekształcić w niezbalansowany obwód z mostkiem typu T, jak pokazano po prawej stronie.

₀ Kiedy Z ₁ Z ₂ = R ² staje się siecią o stałym oporze, która ma tłumienie wtrąceniowe określone przez ${\ Displaystyle T (p) = {\ Frac {R_ {0 }}{R_{0}+Z_{1}(p)}}}$

₀ Po znormalizowaniu do 1 om, źródło, obciążenie i R są równe jedności, więc Z ₁ . Z ₂ = 1, a tłumienie wtrąceniowe staje się

{\ Displaystyle T (p) = {\ Frac {1} {1 + Z_ {1} (p)}}}

W przeszłości tak skonfigurowane obwody były bardzo popularne jako korektory amplitudy. Na przykład były używane do korygowania strat wysokich częstotliwości w kablach telefonicznych i długich odcinkach kabla koncentrycznego w instalacjach telewizyjnych.

Przykład pokazujący procedurę projektowania prostego korektora podano w części dotyczącej syntezy w dalszej części.

Sieci wieloprzepustowe

(Zobacz cytowane wcześniej odniesienia do Zobela, Darlingtona, Bode'a i Guillemina. Zobacz także Stewarta i Weinberga).

Sieci wieloprzepustowe są ważną podklasą sieci kratowych. Stosowano je jako pasywne opóźnienia z elementami skupionymi, jako korektory fazy w sieciach filtrujących oraz w sieciach dyspersyjnych. Są to sieci o stałej rezystancji, dzięki czemu można je łączyć kaskadowo ze sobą iz innymi obwodami bez powodowania problemów z niedopasowaniem.

W przypadku sieci wszechprzepustowych nie ma obszaru tłumienia, więc impedancje $Z a$ i $Z b$ (sieci) są bliźniacze względem siebie przy wszystkich częstotliwościach, a $Z 0$ jest zawsze rezystancyjne, równe $R 0$ .

tj,

{\ Displaystyle Z_ {a} Z_ {b} = R_ {0} ^ {2} \ qquad \ qquad {\ tekst {(przy wszystkich częstotliwościach)}}}

Dla sieci znormalizowanych, gdzie $0 R = 1 ,$ można zapisać funkcję przejścia $T (p) .$

\ Displaystyle T (p) = {\ Frac {1-z_ { a}(p)}{1+z_{a}(p)}}={\frac {z_{b}(p)-1}{z_{b}(p)+1}}}

a więc

{\ Displaystyle z_ {a} (p) = {\ frac {1-T(p)}{1+T(p)}}\qquad {\text{i}}\qquad z_{b}(p)={\frac {1+T(p)}{1 -T(p)}}}

W praktyce $T (p)$ można wyrazić jako stosunek wielomianów w $p$ , a impedancje $z a$ i $z b$ są również stosunkami wielomianów w $p$ . Aby impedancje były możliwe do zrealizowania, muszą spełniać twierdzenie Fostera o reaktancji .

Dwie najprostsze sieci wszechprzepustowe to sieci pierwszego i drugiego rzędu. Są to ważne obwody, ponieważ, jak zauważył Bode, wszystkie wieloprzepustowe sieci kratowe wysokiego rzędu można zastąpić kaskadą sieci drugiego rzędu z prawdopodobnie jedną siecią pierwszego rzędu, aby uzyskać identyczną odpowiedź.

Te dwie proste, znormalizowane sieci mają impedancje przenoszenia podane przez

{\ Displaystyle T_ {1} (p) = {\ Frac {- p+c}{p+c}}\qquad \qquad {\text{i}}\qquad T_{2}(p)={\frac {p^{2}-ap+b}{p^{2 }+ap+b}}}

Obwody są omówione bardziej szczegółowo w sekcji „Synteza”

Synteza sieciowa

Synteza sieci to proces wyprowadzania obwodu w celu dopasowania do wybranej funkcji transferu. Nie wszystkie funkcje transferu mogą być realizowane przez sieci fizyczne, ale dla tych, które mogą, sieć kratowa jest zawsze rozwiązaniem. Innymi słowy, jeśli symetryczna sieć z dwoma parami końcówek jest w ogóle możliwa do zrealizowania, to jest możliwa do zrealizowania jako sieć kratowa. Dzieje się tak dlatego, że struktura kratowa jest najbardziej ogólną formą sieci, z mniejszą liczbą ograniczeń niż, powiedzmy, sieci typu T, П lub mostkowe.

Po opracowaniu obwodu kratowego często pożądane jest przekształcenie wyniku w postać niezrównoważoną, aby obwód mógł być używany w systemach z płaszczyzną uziemienia. Ponadto istnieją inne korzyści, jakie można uzyskać z procesu konwersji, takie jak zmniejszona liczba komponentów i mniej rygorystyczne tolerancje komponentów. Tam, gdzie procedura syntezy daje kilka możliwych rozwiązań sieci, zwykle wybiera się to, które jest najłatwiejsze do konwersji. Często proces konwersji skutkuje wzajemnie sprzężonymi cewkami indukcyjnymi, jak pokazano wcześniej, ale czasami można ich całkowicie uniknąć, jeśli można tolerować wysoką wartość tłumienności wtrąceniowej lub jeśli rozważa się kombinację obwodów równoległych.

Synteza z parametrami z

Parametry z lub parametry impedancji to jeden zestaw z rodziny parametrów definiujących sieć dwuportową, z wartościami wejściowymi i wyjściowymi zdefiniowanymi przez I ₁ , I ₂ , V ₁ i V ₂ , jak pokazano na rysunku.

Sieć dwuportowa

Równania definiujące zachowanie sieci w kategoriach parametrów Z to

{\ Displaystyle {\ rozpocząć {wyrównane} E_ {1} = z_ {11} I_ {1} + z_ {12 }I_{2}\\E_{2}=z_{21}I_{1}+z_{22}I_{2}\end{wyrównane}}}

gdzie parametry z są zdefiniowane w warunkach obwodu otwartego (patrz Parametry impedancji ), dlatego czasami określa się je jako „parametry obwodu otwartego”. Tak są zdefiniowane

{\ Displaystyle z_ {11} = \ lewo [{\ Frac {V_ {1}} {I_ {1} }}}\right]{\text{ with }}I_{2}=0\qquad \qquad z_{12}=\left[{\frac {V_{1}}{I_{2}}}\right] {\text{ z }}I_{1}=0}

{\ Displaystyle z_ {21} = \ lewo [{\ Frac {V_ {2}} {I_ {1 }}}\right]{\text{ with }}I_{2}=0\qquad \qquad z_{22}=\left[{\frac {V_{2}}{I_{2}}}\right] {\text{ z }}I_{1}=0}

W przypadku sieci symetrycznej można łatwo znaleźć zależności między parametrami z a impedancjami sieci i są one

\ Displaystyle z_ {11} = z_ {22} = {\ Frac {Z_ {a} + Z_ {b} }{2}}\qquad z_{12}=z_{21}={\frac {Z_{b}-Z_{a}}{2}}}

{\ Displaystyle Z_ {I} = {\ sqrt {Z_ {a} Z_ {b}}}}

Więc,

{\ Displaystyle Z_ {a} = z_ {11} -z_ {12} \, \ quad Z_ {b} = z_ {11} + z_ {12}}

_można uzyskać przez proste przypisanie części wyrażenia w z 12 _lub w z ₁₁ i z ₁₂ bezpośrednio do impedancji Za _i Zb , jak w poniższym przykładzie.

Przykład 1

Rozważmy, że z ₁₂ jest podane przez

{\ Displaystyle z_ {12} = {\ Frac {p ^ {5}} {(p ^ {2} + 1) (p ^ {2} }+2)}}}

Można to rozszerzyć na ułamki częściowe, aby dać

{\ Displaystyle Z_ {12} = {\ Frac {p} {p ^ {2} + 1}} - {\ Frac {4 p} {p ^{2}+2}}+p}

Przydziel terminy odpowiednio Z _a i Z _b , dając w ten sposób

{\ Displaystyle Z_ {a} = {\ Frac {8p} {p ^ {2} + 2}}}

i

{\ Displaystyle Z_ {b} = {\ Frac {2 p} {p ^ {2} + 1}} + 2 p ={\frac {2p^{3}+4p}{p^{2}+1}}}

Sieć kratowa, która ma te rozwiązania dla Z _a i Z _b , jest pokazana na lewym obwodzie poniżej. Można go przekształcić w postać niezrównoważoną, po pierwsze, wydobywając wspólne równoległe cewki indukcyjne, a po drugie, następnie wydobywając szeregowe wspólne kondensatory. Daje to sieć drabinkową pokazaną na prawym obwodzie.

Synteza z funkcji przenoszenia w obwodzie otwartym

Funkcję przenoszenia stosunku napięcia w obwodzie otwartym T można otrzymać w kategoriach z ₁₁ i z ₁₂ , ponieważ przy I ₂ = 0

{\ Displaystyle T = {\ Frac {V_ {2}} {V_ {1}}} = {\ Frac {z_ {12}} {z_ {11}}}}

więc z wyrażenia na _T , które daje stosunek z ₁₂ do z ₁₁ , można otrzymać obwody dla Za i _Zb .

W praktyce T można wyrazić w postaci

{\ Displaystyle T (p) = K \ cdot {\ Frac {N (p)} {D {p}}}}

gdzie N ( p ) i D ( p ) są wielomianami w p , zespolonej zmiennej częstotliwości, a K jest stałym współczynnikiem mniejszym lub równym jedności.

Dla danego wyrażenia dla T często można znaleźć wyrażenia (a więc obwody dla Za _i Z _b ), pod warunkiem, że wybrana wartość dla K jest wystarczająco mała.

Teraz dla kraty $\ Displaystyle T = {\ Frac {z_ {11}} {z_{12}}}={\frac {Z_{b}-Z_{a}}{Z_{b}+Z_{a}}}={\frac {1-{\frac {Z_{a}} {Z_{b}}}}{1+{\frac {Z_{a}}{Z_{b}}}}}}$

$T} 1+T}}={\frac {D-KN}{D+KN}}}$ za

Procedura ocenia licznik i mianownik wyrażenia jako wielomiany w p, a następnie przypisuje czynniki do Za _i Z _b . Aby wspomóc realizację, może być potrzebny termin straty K, przy K <1.

Przykład 2

Wyprowadź sieć kratową z funkcją przenoszenia stosunku napięcia T ₂ przez

{\ Displaystyle T_ {2} = K \ cdot {\ Frac {p ^ {2} + 1} {p ^ {2} + 5 p + 4} }}

z

{\ Displaystyle K = 1}

i

{\ Displaystyle {\ rozpocząć {wyrównane} D-KN & = p ^ {2} + 5 p + 4-p ^ {2} -1 = 5 p + 3 \\ D + KN & = p ^ {2} + 5 p + 4 + p^{2}+1=2p^{2}+5p+5\end{wyrównane}}}

{\ Displaystyle {\ Frac {Z_ {a}} {Z_ {b}}}={\frac {5p+3}{2p^{2}+5p+5}}={\frac {1+3/5p}{1+(2p^{2}+5)/ 5 pensów}}}

Wybierz ${\ Displaystyle Z_ {a} = 1 + {\ Frac {3} {5p}}}$ i ${\ Displaystyle Z_ {b} = 1+{\frac {2p}{5}}+{\frac {1}{p}}}$

Realizacja kratowa T2 jest pokazana poniżej, _po lewej stronie. Niesymetryczną sieć, po prawej, uzyskuje się najpierw przez wyodrębnienie wspólnych rezystorów szeregowych, a następnie wyodrębnienie pojemności.

Przykład 3

Obwód LC ma funkcję przenoszenia T ₃ określoną przez

{\ Displaystyle T_ {3} = K \ cdot {\ Frac {(p ^ {4} + 1)} {( p^{2}+1)(p^{2}+2)}}}

Jest to możliwe do zrealizowania przy K = 0,05, więc

{\ Displaystyle {\ Frac {D-KN} {D + KN} }={\frac {0,95(p^{4}+3,1579p^{2}+2,0526}{1,05(p^{4}+2,8571p^{2}+1,9524}}={\frac {Z_{a }}{Z_{b}}}}

Faktoryzacja góry i dołu daje

{\ Displaystyle {\ Frac {Z_ {a}} {Z_ {b}}} ={\frac {0,95(p^{2}+0,9153)(p^{2}+2,2426)}{11,05(p^{2}+1,1312)(p^{2}+1,7259)}}}

Wybierz, powiedz,

{\ Displaystyle Z_ {a} = {\ Frac {0,9048 (p ^ {2} + 2,2426 )}{(p^{+}1,1312)}}\qquad {\text{and}}\qquad Z_{b}={\frac {p(p+1,7259)}{p^{2}+0,9153}} }

Za _i Zb można zrealizować jako sieci drabinkowe LC, przy czym Z _a ma cewkę bocznikową jako pierwszy element, a Zb _ma_cewkę szeregową jako pierwszy element, jak pokazano na rysunku po lewej stronie. Tę kratę można przekształcić w postać niezrównoważoną metodami podanymi wcześniej, aby uzyskać wartości składowe figury po prawej stronie,

Synteza Darlingtona

Metoda Darlingtona stanowi podstawę do syntezy bezstratnych sieci dwuparowych z terminacją rezystancyjną dla zadanych charakterystyk przesyłowych.

Sieć metody Darlingtona

Rysunek przedstawia podstawową konfigurację sieci. Powiązana impedancja transferu wynosi

{\ Displaystyle T = {\ Frac {E_ {2}} {I_ {1}}}}

Pierwszym krokiem jest wyrażenie impedancji wejściowej Z1 _zakończonej sieci za pomocą jej parametrów z. To jest

{\ Displaystyle Z_ {I} = {\ Frac {(z_ {11} z_ {22} -z_ {12} ^ {2 })+z_{11}R}{z_{22}+R}}}

gdzie _z11 , _z22 iz12 są parametrami z sieci, jak zdefiniowano wcześniej _. Dla znormalizowanej sieci umieść R = 1 i przestaw wyrażenie w następujący sposób:

{\ Displaystyle Z_ {I} = z_ {11} \ cdot {\ Frac {(z_ {11} z_ { 22}-z_{12}^{2})/z_{11}+1}{z_{22}+1}}}

W praktyce Z _I składa się ze stosunku dwóch wielomianów w p:

{\ Displaystyle Z_ {I} = {\ Frac {N (p)} {D (p)}} = {\ Frac {m_{1}+n_{1}}{m_{2}+n_{2}}}}

gdzie m ₁ i n ₁ to odpowiednio parzyste i nieparzyste części wielomianu licznika, a m ₂ i n ₂ to odpowiednio parzyste i nieparzyste części wielomianu mianownika.

Przestawianie ${\ Displaystyle Z_ {I} = {\ Frac {m_ {1}} {n_ {2}} }\cdot {\frac {(n_{1}/m_{1})+1}{(m_{2}/n_{2})+1}}}$

Porównując dwa wyrażenia dla Z1 _, sugeruje się następujące zależności

{\ Displaystyle z_ {11} = {\ Frac {m_ {1}} {n_ {2} }}\qquad \qquad z_{22}={\frac {m_{2}}{n_{2}}}\qquad \qquad z_{12}={\frac {\sqrt {m_{1}m_{2 }-n_{1}n_{2}}}{n_{2}}}}

Przykład 4

Rozważmy sieć z Z _I przez

{\ Displaystyle Z_ {I} = {\ Frac {2,1351 p ^ {3} + 1,915 p ^ {2} + 2,4969 p+1}{1,327p^{2}+1,18p+1}}}

Więc,

{\ Displaystyle {\ rozpocząć {wyrównane} m_ {1} i = 1,915 p ^ {2} +1&n_{1}&=2,1351p^{3}+1\\m_{2}&=1,327p^{2}+1&n_{2}&=1,18p\end{wyrównane}}}

Więc rozwiązania dla z ₁₁ , z ₂₂ i z ₁₂ są

{\ Displaystyle z_ {11} = {\ Frac {1,915 p ^ {2} + 1} {1,18 p}} = 1,6229 p + {\ Frac { 1}{1,18p}}}

tj. z ₁₁ to cewka indukcyjna 1,6229H połączona szeregowo z kondensatorem 1,18F.

{\ Displaystyle z_ {22} = {\ Frac {1,327 p ^ {2} + 1} {1,18 p}} = 1,1246 p + {\ Frac {1 }{1.18}}}

tj. z ₂₂ to cewka indukcyjna 1,1246H połączona szeregowo z kondensatorem 1,18F

{\ Displaystyle {\ rozpocząć {wyrównane} z_ {12} & = {\ Frac {\ sqrt {(1,915 p ^ {2} + 1) (1,327 p ^ {2} + 1) - (2,1351 p^{3}+2,4969p)}}{1,18p}}\\&={\frac {\sqrt {0,0218p^{4}+0,2957p^{2}+1}}{1,18p}}\ quad ={\frac {0,1479p^{2}+1}{1,18p}}\quad =0,1253p+{\frac {1}{1,18p}}\end{wyrównane}}}

Wyciągając szeregową indukcyjność 0,4983 p = (1,6229 p – 1,1246 p ) z z ₁₁ , pozostała sieć staje się symetryczna z

{\ Displaystyle {\ rozpocząć {wyrównane} z_ {11} ^ {\ tekst {(nowy)}} = z_ { 22}=1,1246p+{\frac {1}{1,18p}}\\z_{12}=0,1253p+{\frac {1}{1,18p}}\end{wyrównane}}}

Składowe sieci symetrycznej można obliczyć ze wzoru Z _a = z ₁₁ − z ₁₂ i Z _b = z ₁₁ + z ₁₂ .

Więc

{\ Displaystyle Z_ {a} = 1,1246 p + {\ Frac {1} {1,18 p}} -0,1253 p - {\ Frac {1 }{1,18p}}=0,9993p,}

tj. induktor 0,9993H.

I

{\ Displaystyle Z_ {b} = 1,1246 p + {\ Frac {1} {1,18 p}} + 0,1253 p + {\ frac {1}{1,18p}}=1,2499p+{\frac {2}{1,18p}},}

tj. induktor 1,2499H szeregowo z kondensatorem 0,59F

Obwód pokazano na lewym rysunku poniżej. Można go łatwo przekształcić w postać niezrównoważoną pokazaną na rysunku po prawej stronie. Jest to filtr dolnoprzepustowy z tętnieniem pasma przepustowego 1,25 dB, z -3 dB przy 0,169 Hz, zerem w paśmie zaporowym przy 0,414 Hz i tłumieniem pasma zaporowego poza częstotliwością zerową poniżej -40 dB.

Synteza sieci kratowych o stałej rezystancji

Jeśli impedancje Z _a i Z _b są podwójne i znormalizowane, tak że

{\ Displaystyle Z_ {a} Z_ {b} = 1}

wówczas impedancja obrazu Z _I staje się czystą rezystancją. Sieć symetryczna spełniająca ten warunek to „sieć o stałym oporze”.

Taką siatkę, zakończoną 1 omem, pokazano poniżej.

Zakończona sieć stałej R

Ma to funkcję przenoszenia

{\ Displaystyle {\ Frac {E_ {2}} {E_ {1}}} = {\ Frac {E_ {2}} { I_{1}}}=T={\frac {1-Z_{a}}{1+Z_{a}}}}

gdzie T jest impedancją przejściową z obciążeniem 1 om w przeciwieństwie do impedancji przejściowej z21 w obwodzie _otwartym . Przeorganizowanie tego daje

{\ Displaystyle Z_ {a} = {\ Frac {1-T} {1 + T}}}

Uważa się zatem, że sieć o stałym oporze oferuje możliwe podejście do syntezy funkcji przenoszenia.

Jest tak, że sieć o stałym oporze jest nie mniej ogólna niż jakakolwiek inna sieć, co oznacza, że każda możliwa do zrealizowania impedancja przenoszenia może być zrealizowana w postaci sieci o stałym oporze. Takie sieci są bardzo wygodne, ponieważ nie ma niedopasowania między sekcjami ani z zakończeniami rezystancyjnymi. W konsekwencji całkowita utrata wtrąceniowa kaskady sekcji o stałej rezystancji jest po prostu sumą poszczególnych sekcji. I odwrotnie, daną skomplikowaną impedancję przejściową można rozłożyć na czynniki multiplikatywne, których poszczególne realizacje sieci, połączone kaskadowo, stanowią syntezę tej impedancji przejściowej. Tak więc, chociaż możliwe jest zsyntetyzowanie pojedynczej sieci o skomplikowanych impedancjach Z _a i Z _b praktycznie łatwiej jest zbudować i zestroić kaskadę prostszych obwodów.

Wszechprzepustowe sieci o stałej rezystancji

Sieci wszechprzepustowe mają stałe wzmocnienie wraz z częstotliwością, ale mają odpowiedź fazową, która zmienia się w wybrany sposób. Na przykład w przypadku sieci opóźniających sieć odpowiedź fazowa jest liniowa z częstotliwością w określonym zakresie częstotliwości, podczas gdy w przypadku sieciowych korektorów fazowych odpowiedź fazowa sieci odchyla się, aby skompensować nieliniową fazę odpowiedź sieci filtrów.

Sieci pierwszego i drugiego rzędu są najważniejsze, ponieważ, jak zauważył Bode, można je łączyć kaskadowo w razie potrzeby, aby uzyskać taki sam wynik, jak skomplikowana sieć wysokiego rzędu.

Przykład 5

Odpowiedź all-pass pierwszego rzędu to

{\ Displaystyle T_ {5} = {\ Frac {cp} {c + p}}}

Ma zero znajdujące się w punkcie + c i biegun w punkcie – c w płaszczyźnie częstotliwości zespolonej. Ma odpowiedź, _w której faza zmienia się wraz z częstotliwością, ale wielkość T5 jest jednością dla wszystkich częstotliwości.

Używając wyrażenia dla Z _a jako funkcji T , z wcześniejszego, daje

{\ Displaystyle Z_ {a} = {\ Frac {1-T_ {5}} {1 + T_ {5}}} = {\ Frac {p} C}}}

Zatem Z _a jest indukcyjnością o wartości 1/ _c , a zatem Zb jest kondensatorem o wartości 1/ c . Sieć, znormalizowana do 1 oma, jest pokazana na lewym rysunku poniżej.

Przykład 6

Odpowiedź all-pass drugiego rzędu to

{\ Displaystyle T_ {6} = {\ Frac {p ^ {2} -ap + b} {p ^ {2} + ap + b} }}

Ma to dwa zera znajdujące się w $Displaystyle -x \ pm y}$ i dwa bieguny w punkcie - $gdzie$ \ a = 2 x i b = x ²² . _Dla takiej odpowiedzi faza zmienia się wraz z częstotliwością, ale wielkość T6 jest równa jedności dla wszystkich częstotliwości.

Dla tej cechy Z _a znajduje się od

{\ Displaystyle Z_ {a} = {\ Frac {1-T_ {6}} {1 + T_ {6}}} = {\ Frac {ap}{p^{2}+b}}}

Więc Z _a jest równoległą kombinacją pojemności 1/a i indukcyjności o wartości a / b . Podobnie Zb jest cewką indukcyjną 1/ a połączoną szeregowo z kondensatorem o wartości a / b _, a sieć jest pokazana po prawej stronie poniżej.

First and second order lattice circuits.png

Sieci kratowe można przekształcić w obwody niezrównoważone, wykorzystując właściwości krat ze wspólnymi elementami zarówno w Z _a, jak i Z _b , pokazane wcześniej, oraz twierdzenie Bartletta o Bisekcji.

Przepustka pierwszego rzędu

Second order bridged-T all pass circuits.png

W przypadku sieci drugiego rzędu, gdy a 2 > b (tj. L 1 > L 2 lub C 2 > C 1 lub y > √ 3 x ), konieczne jest zastosowanie obwodu zawierającego wzajemnie sprzężone cewki dla drugiego rzędu sieć all-pass.

Kaskada sieci drugiego rzędu z być może pojedynczą siecią pierwszego rzędu może być wykorzystana do uzyskania odpowiedzi wysokiego rzędu. Na przykład artykuł Sieć opóźnień kratowych podaje lokalizacje biegunów zerowych dla wielu funkcji transferu wszechprzepustowego, które są zbliżone do liniowej charakterystyki fazowej. Ten artykuł zawiera również kilka przykładów.

Synteza korektorów amplitudy

Typowa ścieżka transmisji ma rosnące straty wraz z częstotliwością i można to skorygować poprzez kaskadowanie systemu z siecią wyrównawczą, która ma rosnącą odpowiedź wraz z częstotliwością. W związku z tym, jedna konfiguracja obwodu, która jest powszechnie stosowana do zapewnienia niezbędnej korekcji, jest pokazana na rysunku oznaczonym „Krata - podstawowy obwód korektora”, podanym wcześniej (w sekcji „Ekwiwalenty niezrównoważone”). Jak stwierdzono tam, tłumienność wtrąceniowa znormalizowanego obwodu jest określona przez ${\ Displaystyle T = {\ Frac {1} {1} {1 + Z_ {1} (p)}}}$ , więc Z ₁ można znaleźć na podstawie ${\ Displaystyle Z_ { 1}(p)={\frac {1}{T(p)}}-1}$

Jeśli dozwolone jest pewne resztkowe tętnienie odpowiedzi, wtedy dla Z1 i Z2 może wystarczyć prosta sieć korygująca _, ale _tętnienie to można zmniejszyć w pożądanym stopniu przez przyjęcie bardziej skomplikowanych sieci korygujących. Wybór lokalizacji biegunów i zer dla Z ₁ i Z ₂ może być wspomagany metodą asymptotyczną linii prostych.

Przykład 7

Funkcją przenoszenia, która ma rosnącą odpowiedź w ograniczonym zakresie częstotliwości, jest

{\ Displaystyle T_ {7} (p )={\frac {3,3333+10,3333p+p^{2}}{30,003+31,003p+p^{2}}}={\frac {(0,3333+p)(10+p)}{(1+ p)(30.003+p)}}}

Zauważ, że odpowiedź zbliża się do jedności przy wysokich częstotliwościach. Może być zrealizowany jako zmostkowany T lub krata, w której _Z1 jest siecią RC.

Z ₁ można znaleźć z ${\ Displaystyle Z_ {1} (p) = {\ Frac {1} {T (p)}} -1}$ . $= {\ Frac {26,6697 + 20,6697 p} {3,3333 + 10,3333 p + p ^ {2}} }}$ )

Admitancję Y ₁ , gdzie Y ₁ = 1/ Z ₁ można wyrazić jako ułamek ciągły zawierający cztery wyrazy, a więc

{\ Displaystyle Y_ {1} (p) = {\ Frac {p ^ {2} + 10,333p+3,3333}{20,6697p+26,6697}}=0,04838+{\cfrac {1}{2,2857+{\cfrac {1}{0,4747p+{\cfrac {1}{5,7153}}}}}}}

Tak więc Z ₁ może być zrealizowany jako sieć drabinkowa RC, na sposób Cauera, i jest pokazany poniżej jako część zmostkowanego obwodu T. Z ₂ jest dualnym Z ₁ , podobnie jak obwód RL, jak pokazano. Równoważny obwód kratowy pokazano po prawej stronie.

Filtry dolnoprzepustowe o stałej rezystancji

Filtry dolnoprzepustowe wysokiego rzędu można uzyskać przez kaskadowanie odpowiedniej liczby prostszych sekcji dolnoprzepustowych o stałej rezystancji.

Pierwsza z tych sekcji dolnoprzepustowych, z tylko jednym biegunem, ma odpowiedź

{\ Displaystyle T_ {1} = {\ Frac {k_{1}}{p+a}}\qquad więc\qquad Z_{a1}={\frac {1-T_{1}}{1+T_{1}}}={\frac {p+(a -k_{1})}{p+(a+k_{1})}}}

Pod warunkiem, że $możliwa$ do zrealizowania impedancja, gdzie Z _{a1 jest kombinacją dwóch rezystorów} pokazano w lewym obwodzie poniżej, a Z _b1 jest podwójnym z Z _a1 . Można to łatwo przekształcić w niezrównoważoną formę, jak pokazano po prawej stronie.

Druga z sekcji filtra, z dwoma biegunami, ma odpowiedź

{\ Displaystyle T_ {2} = k_ {2} {\ Frac {(p + a)} {(p ^ {2} + b_{1}p+b_{0})}}}

Zatem impedancja sieci Z _a2 jest dana wzorem:

{\ Displaystyle Z_ {a2 }={\frac {p^{2}+(b_{1}-k_{2})p+(b_{0}-a.k_{2})}{p^{2}+(b_{1} +k_{2})p+(b_{0}+ak_{2})}}}

Aby zapewnić, że jest to możliwa do zrealizowania sieć, muszą być spełnione pewne warunki

{\ Displaystyle a \ geq 0; \ qquad k_ {2} \ równoważnik b_ {1}; \ qquad k_ {2} \ równoważnik {\ Frac {b_ {0}} {a}}.}

Również

{\ Displaystyle b_ {1} -k_ {2} \ if k_ {2} \ równoważnik b_ {1} -a.}

Warunki wyznaczają granice wartości stałego mnożnika k ₂ w wyrażeniu na T ₂ .

Obwód dla elementów sieciowych Za2 _pokazano po lewej stronie poniżej, a dla elementów podwójnych Zb _pokazano po prawej stronie.

Impedancja Z _a

Impedancja Zb

Wartości składowe dla Z _a to,

{\ Displaystyle {\ rozpocząć {wyrównane} R_ {1} & = {\ Frac {b_ {1} -k_ {2} -a} {2k_ {2}}} i L & = {\ Frac {1} {2k_ {2} }}}\\C&={\frac {2k_{2}}{b_{0}-ab_{1}+a^{2}}}{2ak_{2}}&R_{2}&={\frac { b_{0}-ab_{1}+a^{2}}{2ak-2}}\end{wyrównane}}}

a te dla impedancji Z _b2 to:

{\ Displaystyle {\ rozpocząć {wyrównane} R_ {3} i = {\ Frac {1} {R_ {1}} }\\R_{4}&={\frac {1}{R_{2}}}\\C_{2}&=L_{1}\quad {\text{i}}\quad L_{2}+ C_{1}\end{wyrównane}}}

Niesymetryczna wersja tej sieci jest pokazana poniżej:

Poprzez kaskadowanie pewnej liczby obwodów pierwszego i drugiego rzędu, właśnie opracowanego typu, możliwe jest wyprowadzenie sieci dolnoprzepustowych wyższego rzędu typu:

{\ Displaystyle T_ {n} (p) = {\ Frac {k} {p ^{n}+b_{n-1}p^{n-1}+\cdots +b_{2}p^{2}+b_{1}p+b_{0}}}}

Tak otrzymane sieci kratowe można przekształcić do postaci niezrównoważonej, pod warunkiem, że wartość k jest wystarczająco mała.

Przykład 8

Maksymalnie płaski znormalizowany filtr dolnoprzepustowy trzeciego rzędu ma funkcję przenoszenia

{\ Displaystyle T_ {8} = {\ Frac {k} {p ^ {3} + 2 p ^ {2} + 2 p + 1}}}

Można to rozwinąć jako

{\ Displaystyle T_ {8} = {\ Frac {k_ {1}} {p + a}} \cdot {\frac {k_{2}(p+a)}{p^{2}+p+1}}\cdot {\frac {1}{p+1}}}

Tak więc kaskada trzech krat da wymagany wynik.

Jeśli wymagany jest niezrównoważony obwód, musimy zaakceptować pewne ogólne straty. Wybierając k ₁ = k ₂ = a = 0,5, otrzymujemy sieć pokazaną poniżej. Ten obwód ma całkowitą stratę czterokrotną, podczas gdy konwencjonalna sieć drabinkowa LC nie ma strat (ale nie jest siecią o stałym oporze).

Metody komputerowego wspomagania projektowania

Rozwój komputerów typu mainframe, a następnie komputerów osobistych w ostatniej ćwierci XX wieku umożliwił szybki rozwój technik przetwarzania numerycznego. Początkowo komputery były używane jako pomoc w analizie sieci, następnie w metodach optymalizacji, takich jak metoda minimax, w projektowaniu korektorów faz i filtrów), zanim zostały bezpośrednio zastosowane do syntezy sieci. Przeglądy rozwoju oprogramowania w dziedzinie syntezy zostały podane w Taylor & Huang i Kuo.

Tylko kilka wczesnych programów do syntezy zajmowało się sieciami kratowymi, ale S-Filsyn (potężny program do syntezy i analizy) zapewnia pewne omówienie sieci kratowych i mostkowych obwodów T.

Wczesna historia

Sieci symetryczne i sieci drabinkowe ( filtr stały k i filtr m-derived ) były przedmiotem dużego zainteresowania na początku XX wieku. W tym czasie prężnie rozwijający się przemysł telefoniczny miał znaczący wpływ na rozwój teorii filtrów, dążąc jednocześnie do zwiększenia zdolności przenoszenia sygnału przez telefoniczne linie transmisyjne. George Ashley Campbell był kluczowym współtwórcą tej nowej teorii filtrów, podobnie jak Otto Julius Zobel . Wraz z wieloma współpracownikami pracowali w laboratoriach Western Electric oraz American Telephone and Telegraph Co., a ich prace zostały opisane we wczesnych wydaniach Bell System Technical Journal .

Campbell omówił filtry kratowe w swoim artykule z 1922 roku, podczas gdy inni wcześni pracownicy zainteresowani kratą to Johnson i Bartlett. Artykuł Zobela na temat teorii i projektowania filtrów, opublikowany mniej więcej w tym czasie, wspominał o kratach tylko krótko, z głównym naciskiem na sieci drabinkowe. Dopiero później, gdy Zobel rozważał symulację i wyrównanie telefonicznych linii transmisyjnych, poświęcił więcej uwagi konfiguracji sieci. (Telefoniczne linie transmisyjne w tamtych czasach miały konfigurację zrównoważonych par o nominalnej impedancji charakterystycznej 600 omów, więc korektor sieciowy o swojej zrównoważonej strukturze był szczególnie odpowiedni do użytku z nimi). Szczególnie późniejsi robotnicy Hendrik Wade Bode nadał większe znaczenie sieciom kratowym w swoich projektach filtrów.

W tamtych czasach teoria filtrów opierała się na koncepcjach impedancji obrazu lub teorii filtrów obrazu , która była podejściem projektowym rozwiniętym na podstawie dobrze ugruntowanych badań linii transmisyjnych. Filtr był uważany za skupioną wersję składową odcinka linii transmisyjnej i był jednym z wielu w kaskadzie podobnych odcinków. Jak wspomniano powyżej, słabość podejścia z filtrem obrazu polegała na tym, że odpowiedź częstotliwościowa sieci często nie była taka, jak przewidywano, gdy sieć była zakończona rezystancyjnie, zamiast wymaganych impedancji obrazu. Zasadniczo był to problem niedopasowania i Zobel przezwyciężył go, dopasowując sekcje końcowe. (Widzieć: filtr pochodny m , filtr typu mm ' , ogólny filtr obrazu typu mn , z późniejszymi pracami Payne'a i Bode'a.)

Chociaż filtry kratowe czasami cierpią z powodu tego samego problemu, szereg sieci o stałej rezystancji może go całkowicie uniknąć.

W latach trzydziestych XX wieku, wraz z rozwojem technik analizy i syntezy sieci, projektowanie filtrów drabinkowych metodami obrazowymi stało się mniej popularne. Mimo to koncepcje nadal znajdowały zastosowanie w niektórych nowoczesnych projektach. Z drugiej strony sieci kratowe i ich odpowiedniki obwodów są nadal wykorzystywane w wielu zastosowaniach.

Zobacz też