Kule mniszka lekarskiego

Kule mniszka lekarskiego dotykają bladożółtej płaszczyzny przecinającej stożek.

W geometrii kule mniszka lekarskiego to jedna lub dwie kule , które są styczne zarówno do płaszczyzny , jak i do stożka przecinającego płaszczyznę. Przecięcie stożka i płaszczyzny to przekrój stożkowy , a punkt, w którym którakolwiek z kul styka się z płaszczyzną, jest ogniskiem przekroju stożkowego, dlatego sfery mniszka lekarskiego są czasami nazywane sferami ogniskowymi .

Kule mniszka lekarskiego zostały odkryte w 1822 roku. Zostały nazwane na cześć francuskiego matematyka Germinala Pierre'a Dandelina , chociaż czasami przypisuje się również częściowe uznanie Adolphe'owi Queteletowi .

Sfery Dandelin mogą być użyte do dostarczenia eleganckich, nowoczesnych dowodów dwóch klasycznych twierdzeń znanych Apoloniuszowi z Perge . Pierwsze twierdzenie głosi, że zamknięty przekrój stożkowy (tj. elipsa ) jest miejscem punktów takim, że suma odległości do dwóch stałych punktów (ognisk) jest stała. Drugie twierdzenie mówi, że dla dowolnego przekroju stożkowego odległość od stałego punktu (ogniska) jest proporcjonalna do odległości od linii stałej (kierownicy) , a stała proporcjonalności nazywana jest mimośrodem .

Sekcja stożkowa ma jedną kulę Dandelin dla każdego ogniska. Elipsa ma dwie kule Dandelin dotykające tego samego płaszcza stożka, podczas gdy hiperbola ma dwie kule Dandelin dotykające przeciwległych płaszczy. Parabola ma tylko jedną sferę Dandelin .

Dowód, że krzywa przecięcia ma stałą sumę odległości do ognisk

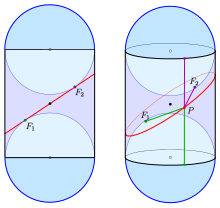
Rozważ ilustrację przedstawiającą stożek z wierzchołkiem S u góry. Płaszczyzna e przecina stożek na krzywej C (z niebieskim wnętrzem). Poniższy dowód pokaże, że krzywa C jest elipsą.

Dwie brązowe kule Dandelin, G 1 i G 2 , są umieszczone stycznie zarówno do płaszczyzny, jak i do stożka: G 1 powyżej płaszczyzny, G 2 poniżej. Każda kula dotyka stożka wzdłuż okręgu (w kolorze białym), i .

Oznaczmy punkt styczności płaszczyzny z G 1 przez F 1 , podobnie dla G 2 i F 2 . Niech P będzie typowym punktem na krzywej C .

Aby udowodnić: Suma odległości pozostaje stała jako punkt P porusza się wzdłuż krzywej przecięcia C . (Jest to jedna definicja 2 { \ displaystyle

  • Linia przechodząca przez P i wierzchołek S stożka przecina te dwa okręgi, stykając się odpowiednio z G1 i G2 w punktach P1 i P2 .
  • Gdy P porusza się po krzywej, P 1 i P 2 poruszają się wzdłuż dwóch okręgów, a ich odległość d ( P 1 , P 2 ) pozostaje stała.
  • Odległość od P do F 1 jest taka sama jak odległość od P do P 1 , ponieważ odcinki linii PF 1 i PP 1 są styczne do tej samej kuli G 1 .
  • Z symetrycznego argumentu wynika, że ​​odległość od P do F 2 jest taka sama jak odległość od P do P 2 .
  • W konsekwencji obliczamy sumę odległości jako , która jest stała, gdy P porusza się wzdłuż krzywej.

Daje to inny dowód twierdzenia Apoloniusza z Perge .

Jeśli zdefiniujemy elipsę jako zbiór punktów P takich, że d ( F 1 , P ) + d ( F 2 , P ) = stała, to powyższy argument dowodzi, że krzywa przecięcia C jest rzeczywiście elipsą. To, że przecięcie płaszczyzny ze stożkiem jest symetryczne względem dwusiecznej prostej przechodzącej przez F1 i F2 , może być sprzeczne z intuicją, ale ten argument wyjaśnia.

Obudowa cylindra

Adaptacje tego argumentu działają dla hiperbol i parabol jako przecięć płaszczyzny ze stożkiem. Kolejna adaptacja działa dla elipsy zrealizowanej jako przecięcie płaszczyzny z prawym kołowym walcem .

Dowód właściwości focus-directrix

Kierownicę przekroju stożkowego można znaleźć za pomocą konstrukcji Jaskra. Każda kula mniszka lekarskiego przecina stożek po okręgu; niech oba te okręgi określą swoje własne płaszczyzny. Przecięcia tych dwóch równoległych płaszczyzn z płaszczyzną przekroju stożkowego będą dwiema równoległymi liniami; te linie są kierownicami przekroju stożkowego. Jednak parabola ma tylko jedną sferę Dandelin, a zatem ma tylko jedną kierownicę.

Za pomocą sfer Dandelin można udowodnić, że dowolny przekrój stożkowy jest miejscem punktów, dla których odległość od punktu (ogniska) jest proporcjonalna do odległości od kierownicy. Starożytni greccy matematycy, tacy jak Pappus z Aleksandrii , byli świadomi tej właściwości, ale sfery Dandelin ułatwiają dowód.

Ani Dandelin, ani Quetelet nie użyli sfer Dandelin, aby udowodnić właściwość focus-directrix. Pierwszym, który to zrobił, mógł być Pierce Morton w 1829 r., A może Hugh Hamilton , który zauważył (w 1758 r.), Że kula dotyka stożka na okręgu, który definiuje płaszczyznę, której przecięcie z płaszczyzną przekroju stożka jest kierownicą. Właściwość focus-directrix może być wykorzystana do udowodnienia, że ​​obiekty astronomiczne poruszają się po odcinkach stożkowych wokół Słońca.

Notatki

  1. ^ abc Karol . Taylor, Wprowadzenie do starożytnej i współczesnej geometrii stożków , strona 196 („sfery ogniskowe”) , strony 204–205 (historia odkrycia) (Deighton, Bell i współpracownicy, 1881).
  2. ^ Jaskier, G. (1822). „Mémoire sur quelques propriétés remarquables de la focale parabolique” [Pamiętnik o niektórych niezwykłych właściwościach ogniska parabolicznego [ tj. Ukośnej strofoidy ]]. Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Bruxelles (w języku francuskim). 2 : 171–200.
  3. Bibliografia _ Stożki , str. 86 (dowód na elipsę) i s. 141 (dla hiperboli) (Cambridge University Press, 2005).
  4. ^ Quetelet, Adolphe (1819) „Dissertatio mathematica inauguralis de quibusdam locis geometricis nec non de curva focali” (inauguracyjna rozprawa matematyczna na temat niektórych loci geometrycznych, a także krzywych ogniskowych), praca doktorska (Uniwersytet w Gandawie („Gand”), Belgia). (po łacinie)
  5. ^ Godeaux, L. (1928). „Mathématicien Adolphe Quetelet (1796-1874)” . Ciel et Terre (w języku francuskim). 44 : 60–64.
  6. ^ abc Heath , Thomas . A History of Greek Mathematics , strona 119 (właściwość focus-directrix) , strona 542 (suma odległości do właściwości ognisk) (Clarendon Press, 1921).
  7. ^ Brannan, A. i in. Geometria , strona 19 (Cambridge University Press, 1999).
  8. ^ Biografie Numericany: Morton, Pierce
  9. Bibliografia _ Geometria, płaszczyzna, bryła i kula, w sześciu księgach , strona 228 (Baldwin i Cradock, 1830).
  10. ^ Morton Pierce (1830). „W ognisku sekcji stożkowej” . Transakcje Towarzystwa Filozoficznego Cambridge . 3 : 185–190.
  11. Bibliografia _ De Sectionibus Conicis. Tractatus Geometricus. In quo, ex Natura ipsius Coni, Sectionum Affectiones facillime deducuntur. Methodo nova [ Na przekrojach stożkowych. Traktat geometryczny. W którym z natury samego stożka najłatwiej wydedukować stosunki przekrojów. Nową metodą. ] (po łacinie). Londyn, Anglia: William Johnston. s. 122–125. Liber (księga) II, Propositio (propozycja) XXXVII (37).
  12. Bibliografia _ „Proste kartezjańskie traktowanie ruchu planetarnego”, European Journal of Physics , tom. 14, strona 145 (1993).

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Dandelin_spheres&oldid=1147402046 ”