Lasso (statystyki)

Ten artykuł dotyczy statystyki i uczenia maszynowego. W przypadku innych zastosowań zobacz Lasso (ujednoznacznienie) .

W statystyce i uczeniu maszynowym lasso ( operator najmniejszego bezwzględnego skurczu i selekcji ; także Lasso lub LASSO ) to metoda analizy regresji , która przeprowadza zarówno selekcję zmiennych , jak i regularyzację w celu zwiększenia dokładności przewidywania i możliwości interpretacji wynikowego modelu statystycznego . Został pierwotnie wprowadzony w geofizyce , a później przez Roberta Tibshiraniego , który ukuł ten termin.

Lasso został pierwotnie opracowany dla modeli regresji liniowej . Ten prosty przypadek ujawnia znaczną ilość informacji o estymatorze. Obejmują one jego związek z regresją grzbietową i wyborem najlepszego podzbioru oraz powiązania między oszacowaniami współczynników lassa a tak zwanym miękkim progowaniem. Ujawnia również, że (podobnie jak w przypadku standardowej regresji liniowej) oszacowania współczynników nie muszą być unikalne, jeśli współzmienne są współliniowe .

Chociaż pierwotnie zdefiniowano ją dla regresji liniowej, regularyzacja lassem może być łatwo rozszerzona na inne modele statystyczne, w tym uogólnione modele liniowe , uogólnione równania estymacji , modele proporcjonalnego hazardu i M-estymatory . Zdolność Lasso do przeprowadzania selekcji podzbiorów opiera się na formie ograniczenia i ma różne interpretacje, w tym pod względem geometrii , statystyki bayesowskiej i analizy wypukłej .

LASSO jest ściśle powiązany z odszumianiem pościgu za bazą .

Historia

Lasso zostało wprowadzone w celu poprawy dokładności przewidywania i interpretowalności modeli regresji. Wybiera zredukowany zestaw znanych współzmiennych do wykorzystania w modelu.

Lasso został opracowany niezależnie w literaturze geofizycznej w 1986 roku na podstawie wcześniejszych prac, w których zastosowano $karę$ zarówno za , jak i penalizację współczynników Statystyk Robert Tibshirani niezależnie odkrył go na nowo i spopularyzował w 1996 roku na podstawie nieujemnej garoty Breimana .

Przed lassem najczęściej stosowaną metodą wyboru współzmiennych była selekcja krokowa . Takie podejście poprawia dokładność przewidywania tylko w niektórych przypadkach, na przykład gdy tylko kilka współzmiennych ma silny związek z wynikiem. Jednak w innych przypadkach może zwiększyć błąd prognozy.

W tamtym czasie regresja grzbietu była najpopularniejszą techniką poprawiania dokładności prognoz. Regresja grzbietowa poprawia błąd predykcji, zmniejszając sumę kwadratów współczynników regresji do wartości mniejszej niż ustalona wartość w celu zmniejszenia nadmiernego dopasowania , ale nie przeprowadza selekcji współzmiennych, a zatem nie ułatwia interpretacji modelu.

Lasso osiąga oba te cele, wymuszając, aby suma wartości bezwzględnych współczynników regresji była mniejsza niż stała wartość, co wymusza na niektórych współczynnikach zero, wykluczając je z wpływu na prognozy. Pomysł ten jest podobny do regresji grzbietowej, która również zmniejsza rozmiar współczynników; jednak regresja grzbietowa nie ustawia współczynników na zero (a zatem nie przeprowadza selekcji zmiennych ).

Podstawowa forma

Najmniejsze kwadraty

Rozważmy próbę składającą się z N przypadków, z których każdy składa się z p współzmiennych i pojedynczego wyniku. Niech ${\ Displaystyle y_ {i}}$ będzie wynikiem i ${\ Displaystyle x_ {i}: = (x_ {1}, x_ { 2},\ldots ,x_{p})_{i}^{T}}$ będzie wektorem współzmiennym dla i- ^tego przypadku. Wtedy celem lassa jest rozwiązanie

${\ Displaystyle \ min _ {\ beta _ {0}, \ beta} \ lewo \ {\ suma _ {i = 1} ^ {N} (y_ {i} - \ beta _ {0} -x_ {i} ^{T}\beta )^{2}\right\}{\text{podlega }}\sum _{j=1}^{p}|\beta _{j}|\leq t.}$

Tutaj ${\ Displaystyle \ beta _ {0}}$ jest stałym współczynnikiem, ${\ Displaystyle \ beta: = (\ beta _ {1}, \ beta _ {2}, \ ldots, \ beta _ {p}}}$ jest wektorem współczynników, a jest $określonym$ parametrem swobodnym, który określa stopień uregulowania.

${\ Displaystyle X}$ będzie macierzą współzmiennych, tak że ${\ Displaystyle X_ {ij} = (x_ {i}) _ {j}}$ i ${\ Displaystyle x_ {i}^{T}}$ to i ^-ty wiersz ${\ displaystyle X}$ , wyrażenie można zapisać bardziej zwięźle jako X {\ displaystyle X}

${\ Displaystyle \ min _ {\ beta _ {0}, \ beta} \ lewo \ {\ lewo \ | y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}{\text{ podmiot }}\|\beta \|_{1}\leq t, }$

gdzie $| ^ {p} \ right) ^ {1/p}}$${\ Displaystyle \|u \ | _ {p} = \ lewo (\ suma _ {i = 1} ^ {N} | u_ {i$${\ displaystyle \ ell ^ {p}}$ } jest normą .

Oznaczając średnią skalarną punktów danych przez ${\ displaystyle x_ {i}}$ przez ${\ displaystyle {\ bar {x}}}$ i średnią zmiennych odpowiedzi przez x $\ displaystyle y_ {i}}$${\ Displaystyle {\ bar {y}}}$ , wynikowe oszacowanie dla ${\ Displaystyle \ beta _ {0}}$ to ${\ Displaystyle {\ hat {\ beta}} _ {0} = {\ bar {y}} - {\ bar {x}} ^ {T} \ beta}, tak$ że

${\ Displaystyle y_ {i} - {\ kapelusz {\ beta}} _ {0} -x_ {i} ^ {T} \ beta = y_ {i} - ({\ bar {y}} - {\ bar { x}}^{T}\beta )-x_{i}^{T}\beta =(y_{i}-{\bar {y}})-(x_{i}-{\bar {x}} )^{T}\beta ,}$

dlatego standardem jest praca ze zmiennymi, dla których średnia wynosi zero. Ponadto współzmienne są zwykle standaryzowane ${\ Displaystyle \ textstyle \ lewo (\ suma _ {i = 1} ^ {N} x_ {i} ^ {2} = 1 \ po prawej)}$ , aby rozwiązanie nie zależało od skali pomiaru.

Przepisanie może być pomocne

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {{\ Frac {1} {N}} \ lewo \ | yX \ beta \ prawo \ |_ {2} ^{2}\right\}{\text{z zastrzeżeniem }}\|\beta \|_{1}\leq t.}$

w tak zwanej postaci Lagrange'a

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {{\ frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda \|\beta \|_{1}\right\}}$

$.$ dokładny związek między $i$ od danych

Współzmienne ortonormalne

Można teraz rozważyć niektóre podstawowe właściwości estymatora lassa.

Zakładając najpierw, że współzmienne są ortonormalne , tak że $} ^ {T} x_ {j} = \ delta _ {ij}}$ δ ${ij}}$$\ Displaystyle \ delta$$można$ to delta Kroneckera równoważnie , za pomocą metod podgradientowych ,

${\ Displaystyle {\ rozpocząć {wyrównane} {\ kapelusz {\ beta}} _ {j} = {} & S _ {N \ lambda} ({\ kapelusz {\ beta}} _ {j} ^ {\ tekst {OLS} })={\hat {\beta}}_{j}^{\text{OLS}}\max \left(0,1-{\frac {N\lambda}}{|{\hat {\beta}} _{j}^{\text{OLS}}|}}\right)\\&{\text{ gdzie }}{\hat {\beta }}^{\text{OLS}}=(X^{T }X)^{-1}X^{T}y=X^{T}y\koniec{wyrównany}}}$

${\ Displaystyle S _ {\ alfa}}$ jest określany jako operator progowania miękkiego , ponieważ tłumaczy wartości w kierunku zera (czyniąc je dokładnie zerowymi, jeśli są wystarczająco małe) zamiast ustawiania mniejszych wartości na zero i pozostawiania większych nietkniętych jako S α {\ displaystyle S _ {\ alfa}} twardy operator progowania , często oznaczany $,$ to

W regresji grzbietowej celem jest minimalizacja

${\ Displaystyle \ min _ {\ beta \ in \ mathbb {R} ^ {p}} \ lewo \ {{{ \frac {1}{N}}\|yX\beta \|_{2}^{2}+\lambda \|\beta \|_{2}^{2}\right\}}$

Używając wzoru regresji grzbietu: $X$${ \beta }}=\left((X^{T}X)+N\lambda I\right)^{-1}X^{T}y} , daje to$ :

${\ Displaystyle {\ kapelusz {\ beta}} _ {j} = (1 + N \ lambda) ^ {-1} {\ kapelusz {\ beta}} _ {j} ^ {\ tekst {OLS}}.}$

$zmniejsza$ jednolity współczynnik nie ustawia żadnych .

Można to również porównać do regresji z wyborem najlepszego podzbioru , w której celem jest minimalizacja

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {{\ Frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda \|\beta \|_{0}\right\}}$

gdzie ${\ Displaystyle \|\ cdot \|_ {0}}$$jest$ normą która jest zdefiniowana jako ${\ Displaystyle \| z \|=m}$ jeśli dokładnie m składników z jest niezerowych. W tym przypadku można to wykazać

${\ Displaystyle {\ kapelusz {\ beta}} _ {j} = H_ {\ sqrt {N\lambda}}\left({\kapelusz {\beta}}_{j}^{\text{OLS}}\right)={\kapelusz {\beta}}_{j}^{\tekst{ OLS}}\mathrm {I} \left(\left|{\hat {\beta }}_{j}^{\text{OLS}}\right|\geq {\sqrt {N\lambda }}\right )}$

gdzie jest tak zwaną twardą funkcją progową i $jest$ wskaźnika (jest to 1, jeśli jej argument jest prawdziwy, a 0 w przeciwnym $)$

Dlatego oszacowania lassa mają wspólne cechy zarówno regresji grzbietowej, jak i regresji wyboru najlepszego podzbioru, ponieważ oba zmniejszają wielkość wszystkich współczynników, takich jak regresja grzbietowa, i ustawiają niektóre z nich na zero, jak w przypadku wyboru najlepszego podzbioru. Dodatkowo, podczas gdy regresja grzbietowa skaluje wszystkie współczynniki o stały współczynnik, lasso zamiast tego tłumaczy współczynniki w kierunku zera o stałą wartość i ustawia je na zero, jeśli osiągną tę wartość.

Skorelowane zmienne towarzyszące

W jednym szczególnym przypadku dwie zmienne towarzyszące, powiedzmy j i k , są identyczne dla każdej obserwacji, więc ${\ Displaystyle x_ {(j)} = x_ {(k)}}$ , gdzie ${\ Displaystyle x_ {(j), i} = x_ {(k), i}}$ . Następnie wartości ${\ displaystyle \ beta _ {j}}$ i ${\ displaystyle \ beta _ {k}}$ , które minimalizują funkcję celu lassa, nie są jednoznacznie określone. W rzeczywistości, jeśli jakiś ${\ Displaystyle {\ kapelusz {\ beta}}}$ w którym ${\ Displaystyle {\ kapelusz {\ beta}} _ {j} {\ kapelusz {\ beta} } _ {k} \ geq 0}$ , to jeśli ${\ Displaystyle s \ w [0,1]}$ zastępując ${\ Displaystyle {\ kapelusz {\ beta}} _ {j}}$ przez ${\ Displaystyle s ({\ kapelusz {\ beta}} _ {j} + {\ kapelusz {\ beta}} _ {k})} i β ^ k {\$ Displaystyle ${ \ beta}} _ {k}}$ przez ${\ Displaystyle (1-s) ({\ kapelusz {\ beta}} _ {j} + {\ kapelusz { \ beta}} _ {k})}$ , zachowując wszystkie pozostałe ${\ Displaystyle {\ hat {\ beta}} _ {i}}$ naprawiony, daje nowe rozwiązanie, więc funkcja celu lasso ma wtedy kontinuum ważnych minimalizatorów. Aby rozwiązać ten problem, zaprojektowano kilka wariantów lassa, w tym regularyzację elastycznej sieci .

Formularz ogólny

Regularyzację Lasso można rozszerzyć na inne funkcje celu, takie jak te dla uogólnionych modeli liniowych , uogólnionych równań estymujących , modeli proporcjonalnego hazardu i M-estymatorów . Biorąc pod uwagę funkcję celu

${\ Displaystyle {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} f (x_ {i} ,y_{i},\alfa,\beta)}$

rozwiązaniem estymatora jest uregulowana lassem wersja estymatora

${\ Displaystyle \ min _ {\ alfa, \ beta} {\ Frac {1} {N}}\sum _{i=1}^{N}f(x_{i},y_{i},\alpha ,\beta ){\text{ podmiot }}\|\beta \|_{ 1}\równik t}$

gdzie tylko $}$$może$$beta$ jest karane, podczas gdy przyjąć dowolną dozwoloną wartość, tak jak nie było karane w podstawowym przypadku

Interpretacje

Interpretacja geometryczna

Formy obszarów ograniczających dla regresji lassowej i grzbietowej.

Lasso może ustawić współczynniki na zero, podczas gdy powierzchownie podobna regresja grzbietu nie. Wynika to z różnicy w kształcie ich granic ograniczających. Zarówno regresję lasso, jak i regresję grzbietową można interpretować jako minimalizację tej samej funkcji celu

${\ Displaystyle \ min _ {\ beta _ {0}, \ beta} \ lewo \ {{\ Frac {1} {N}} \ lewo\|y-\beta _{0}-X\beta \prawo\|_{2}^{2}\prawo\}}$

ale w odniesieniu do różnych ograniczeń: ${\ Displaystyle \|\ beta \|_ {1} \ równoważnik t}$ dla lasso i ${\ Displaystyle \|\ beta \|_ {2}^{2}\leq t}$ dla grzbietu. Rysunek pokazuje, że region ograniczeń zdefiniowany przez $polytope$ jest kwadratem obróconym tak, że jego rogi leżą na osiach (ogólnie cross ) , podczas gdy region zdefiniowany przez ${\ displaystyle \ ell ^ {2}}$ norma to okrąg (ogólnie n -sfera ), który jest niezmienny obrotowo i dlatego nie ma rogów. Jak widać na rysunku, wypukły obiekt, który leży stycznie do granicy, taki jak pokazana linia, prawdopodobnie napotka róg (lub odpowiednik o wyższych wymiarach) hipersześcianu, dla którego niektóre składniki β {\ $\ beta }$ są identycznie zerowe, podczas gdy w przypadku n -sfery punkty na granicy, dla których niektóre składowe ${\ displaystyle \ beta}$$, nie różnią$ od innych, a wypukły przedmiot nie ma większego prawdopodobieństwa zetknięcia się z punktem, w którym niektóre składniki są równe zeru niż jeden, dla którego żaden z nich nie jest.

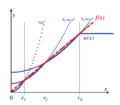
Ułatwienie interpretacji λ dzięki kompromisowi między dokładnością a prostotą

$,$ aby łatwo było przewidzieć i wpłynąć na stopień skurczu związany z daną . Zakłada się, że $zerowa$ z wynikami Z i że $jest wyśrodkowany$ ). Niech $reprezentuje$ hipotetyczne współczynniki regresji i niech $\ Displaystyle b_ {OLS}}$ zapoznaj się ze zwykłymi rozwiązaniami najmniejszych kwadratów zoptymalizowanymi pod kątem danych. Następnie możemy zdefiniować Lagrange'a jako kompromis między dokładnością w próbce rozwiązań zoptymalizowanych pod kątem danych a prostotą trzymania się hipotetycznych wartości. To skutkuje

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {{\ Frac {(yX \ beta) '(yX \ beta)} {(yX \ beta _ {0} )'(yX\beta _{0})}}+2\lambda \sum _{i=1}^{p}{\frac {|\beta _{i}-\beta _{0,i}| }{q_{i}}}\prawo\}}$

gdzie ${\ displaystyle q_ {i}}$ jest określony poniżej. Pierwszy ułamek reprezentuje względną dokładność, drugi ułamek względną prostotę, a $równowaga$ nimi.

$ell _ {2}}$$_ {1}}$ dla i normy, gdy $Displaystyle \ ell$ i β ${\ Displaystyle \ beta _ {0} = 0}$

$pod uwagę pojedynczy regresor,$ można zdefiniować, określając jako ${\ Displaystyle | b_ {OLS} - \ beta _ {0}|}$ , czyli maksymalna wielkość odchylenia od ${\ Displaystyle \ beta _ {0}}$ , gdy ${\ Displaystyle \ lambda = 0}$ . Zakładając, że $2$ zdefiniować za pomocą ${\ Displaystyle R ^ {2}}$ :

${\ Displaystyle b _ {\ ell _ {1}} = {\ rozpocząć {przypadki} (1- \ lambda / R ^ {2}) b_ {OLS} i {\ mbox {if}} \ lambda \ równoważnik R ^ { 2},\\0&{\mbox{if}}\lambda >R^{2}.\end{przypadki}}}$

Jeśli ${\ displaystyle \ lambda = 0}$ , używane jest zwykłe rozwiązanie najmniejszych kwadratów (OLS). Hipotetyczna wartość $2$$}$ { \ ${2}$ . Ponadto, jeśli , to reprezentuje proporcjonalny wpływ $\ Displaystyle$$R ^ {2} = 1$${\ Displaystyle \ beta _ {0} = 0}$ . Innymi słowy, $danych$ minimalny wpływ hipotetycznej wartości w stosunku do rozwiązania OLS zoptymalizowanego pod

Jeśli -norm jest używany do karania odchyleń od zera przy pojedynczym regresorze, ścieżka rozwiązania jest określona przez ${\ displaystyle \ ell _ {2}}$

${\ Displaystyle b _ {\ ell _ {2}} = {\ bigg (} 1 + {\ Frac {\ lambda}} R^{2}(1-\lambda)}}{\bigg)}^{-1}b_{OLS}}$ . Jak ${\ Displaystyle b _ {\ ell _ {1}}}$ , ${\ Displaystyle b _ {\ ell _ {2}}}$ porusza się w kierunku punktu ${\ Displaystyle (\ lambda = R ^ {2}, b = 0)}$ kiedy $jest$ bliskie zeru ale w przeciwieństwie do ${\ Displaystyle b _ {\ ell _ {1}}}$$_ {2}} }$$ℓ$ 2 { jeśli $rysunek$ ).
$, w którym parametr jest aktywowany ($$)$ . może odbiegać od regresora w dokładność. Pierwszy,

${\ Displaystyle R ^ {2} = 1 - {\ Frac {(y-Xb) '(y-Xb)} {(yX \ beta _ {0}) '(yX \ beta _ {0})}}. }$

Wartość $75$ jeśli zamiast hipotetycznych wartości zostaną użyte $OLS$ . Indywidualny wkład odejścia od każdej hipotezy można obliczyć za pomocą macierzy ${\ displaystyle p}$ x ${\ displaystyle p}$

${\ Displaystyle R ^ {\ otimes} = (X '{\ tylda { y}}_{0})(X'{\tylda {y}}_{0})'(X'X)^{-1}({\tylda {y}}_{0}'{\tylda {y}}_{0})^{-1},}$

gdzie ${\ Displaystyle {\ tylda {y}} _ {0} = yX \ beta _ {0}}$ . Jeśli ${\ Displaystyle b = b_ {OLS}}$ , gdy oblicza się ${\ Displaystyle R ^ {2}} , to$ suma elementów ukośnych ${\ Displaystyle R ^ {\ otimes}}$ do ${\ Displaystyle R ^ {2}}$ . Przekątna ${\ Displaystyle R ^ {\ otimes}}$$Displaystyle$ niż 0 lub, rzadziej, większe niż 1. Jeśli regresory są nieskorelowane, to po element przekątny $R ^ {\ otimes}}$ odpowiada wartości między $r$$displaystyle$ } a $.$

Przeskalowaną wersję lassa adaptacyjnego można uzyskać ustawiając ${\ Displaystyle q_ {{\ mbox {lasso adaptacyjne}}, i} = | b_ {OLS, i} - \ beta _ {0, i} |}$ . Jeśli regresory są nieskorelowane, moment $^ {$ { \ $th$${\ Displaystyle R ^ {\ otimes}}$ . Zakładając dla wygody, że jest wektorem zer, ${\ displaystyle \ beta _ {0}}$

${\ Displaystyle b_ {i} = {\ rozpocząć {przypadki} (1- \ lambda / R_ {ii} ^ {\ otimes}) b_ {OLS, i} & {\ mbox {if}} \ lambda \ leq R_ { ii}^{\otimes},\\0&{\mbox{if}}\lambda >R_{ii}^{\otimes}.\end{przypadki}}}$

$displaystyle \ beta _ {0}}$ to, że jeśli regresory są nieskorelowane, ponownie określa minimalny wpływ $\$ . Nawet jeśli regresory są skorelowane, po raz pierwszy aktywowany $R ^ {\ otimes}}$ parametr regresji, gdy jest równy najwyższemu elementowi ukośnemu $Displaystyle$ .

Wyniki te można porównać z przeskalowaną wersją lassa, definiując ${\ Displaystyle q _ {{\ mbox {lasso}}, i} = {\ Frac {1} {p}} \ suma _ {l} | b_ {OLS, l} - \ beta _ {0, l} |}$ , czyli średnie bezwzględne odchylenie od ${\ Displaystyle b_ {OLS}}$ od ${\ Displaystyle \ beta _ {0}}$ . Zakładając, że regresory są nieskorelowane, to moment aktywacji regresora jest określony przez ${\ displaystyle i ^ {th}}$

${\ Displaystyle {\ tylda {\ lambda}} _ {{\ tekst {lasso}}, i} = {\ Frac {1} {p}} {\ sqrt {R_ {i} ^ {\ otimes}}} \ suma _{l=1}^{p}{\sqrt {R_{l}^{\czasami}}}.}$

p ${\ Displaystyle p = 1}$ moment aktywacji jest ponownie podany przez ${\ Displaystyle {\ tylda {\ lambda}} _ {{\ tekst {lasso}},$ . Jeśli $zer$ i podzbiorem odpowiednich parametrów są w równym stopniu odpowiedzialne za idealne dopasowanie $R$${2}=1}$$R$$displaystyle {\ frac {1} {p}}}$ wtedy ten podzbiór jest aktywowany przy wartości $\$ . Moment aktywacji odpowiedniego regresora jest wtedy równy ${\ Displaystyle {\ Frac {1} {p}} {\ Frac {1} {\ sqrt {p_ {B} }}}p_{B}{\frac {1}{\sqrt {p_{B}}}}={\frac {1}{p}}}$ . Innymi słowy, włączenie nieistotnych regresorów opóźnia moment aktywacji odpowiednich regresorów przez to przeskalowane lasso. Lasso adaptacyjne i lasso to szczególne przypadki estymatora „1ASTc”. Ten ostatni grupuje parametry tylko wtedy, gdy bezwzględna korelacja między regresorami jest większa niż wartość określona przez użytkownika.

Interpretacja bayesowska

Rozkłady Laplace'a mają ostry szczyt w ich średniej z większą koncentracją gęstości prawdopodobieństwa w porównaniu z rozkładem normalnym.

Tak jak regresję grzbietową można interpretować jako regresję liniową, której współczynnikom przypisano normalne rozkłady a priori , tak lasso można interpretować jako regresję liniową, dla której współczynniki mają rozkłady a priori Laplace'a . Rozkład Laplace'a ma ostry szczyt przy zerze (jego pierwsza pochodna jest nieciągła przy zerze) i koncentruje swoją masę prawdopodobieństwa bliżej zera niż rozkład normalny. Zapewnia to alternatywne wyjaśnienie, dlaczego lasso ma tendencję do ustawiania niektórych współczynników na zero, podczas gdy regresja grzbietu nie.

Interpretacja relaksacji wypukłej

Lasso można również postrzegać jako wypukłą relaksację problemu regresji wyboru najlepszego podzbioru, polegającego na znalezieniu podzbioru współzmiennych, $który$ najmniejszą wartość funkcji celu dla pewnego ${\ displaystyle k \ równoważnik n}$ , gdzie n jest całkowitą liczbą współzmiennych. Norma „ ${\ Displaystyle \ ell ^ {0}}$$} ($ granicznym przypadkiem " ${\ Displaystyle \ ell ^ {p}}$ normy", postaci ${\ Displaystyle \ textstyle \|x\|_ {p }=\left(\sum _{i=1}^{n}|x_{j}|^{p}\right)^{1/p}} (gdzie cudzysłowy oznaczają, że tak naprawdę nie są to normy$ dla ${\ displaystyle p <1}$ od ${\ Displaystyle \|\ cdot \|_ {p}}$ nie jest wypukła dla ${\ Displaystyle p <1}$ , więc nierówność trójkąta nie zachodzi). Dlatego, ponieważ p = 1 jest najmniejszą wartością, dla której $norma$ najlepszym wypukłym przybliżeniem do najlepszy problem wyboru podzbioru, ponieważ region zdefiniowany przez ${\ Displaystyle \|x\|_ {1}\ równoważnik t}$ jest otoczką wypukłą regionu zdefiniowanego przez ${\ Displaystyle \|x \|_ {p} \ równoważnik t}$ dla ${\ Displaystyle p <1}$ .

Uogólnienia

Warianty lasso zostały stworzone, aby zaradzić ograniczeniom oryginalnej techniki i uczynić metodę bardziej przydatną do określonych problemów. Prawie wszystkie z nich koncentrują się na poszanowaniu lub wykorzystaniu zależności między współzmiennymi.

Elastyczna regularyzacja sieci dodaje dodatkową karę podobną do regresji grzbietowej, która poprawia wydajność, gdy liczba predyktorów jest większa niż wielkość próby, pozwala metodzie wybrać razem silnie skorelowane zmienne i poprawia ogólną dokładność predykcji.

Lasso grupowe umożliwia wybranie grup powiązanych zmiennych towarzyszących jako pojedynczej jednostki, co może być przydatne w ustawieniach, w których nie ma sensu uwzględnianie niektórych zmiennych towarzyszących bez innych. Dalsze rozszerzenia lassa grupowego wykonują selekcję zmiennych w obrębie poszczególnych grup (rzadkie lasso grupowe) i umożliwiają nakładanie się grup (lasso grupowe nakładania się).

Połączone lasso może uwzględniać przestrzenną lub czasową charakterystykę problemu, dając oszacowania, które lepiej pasują do struktury systemu. Modele uregulowane lasso można dopasować przy użyciu technik, w tym metod subgradientowych , regresji najmniejszych kątów (LARS) i metod proksymalnych gradientów . Określenie optymalnej wartości parametru regularyzacji jest ważną częścią zapewnienia dobrego działania modelu; jest zwykle wybierany za pomocą walidacji krzyżowej .

Elastyczna siatka

Główny artykuł: Elastyczna regularyzacja sieci

W 2005 roku Zou i Hastie wprowadzili elastyczną siatkę . Kiedy p > n (liczba współzmiennych jest większa niż wielkość próby), lasso może wybrać tylko n współzmiennych (nawet jeśli więcej jest powiązanych z wynikiem) i ma tendencję do wybierania jednej współzmiennej z dowolnego zestawu wysoce skorelowanych współzmiennych. Dodatkowo, nawet gdy n > p , regresja grzbietu zwykle działa lepiej, biorąc pod uwagę silnie skorelowane zmienne towarzyszące.

Elastyczna siatka rozciąga lasso, dodając dodatkowy termin kary, dając ${\ displaystyle \ ell ^ {2}}$

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p }}\left\{\left\|yX\beta \right\|_{2}^{2}+\lambda _{1}\|\beta \|_{1}+\lambda _{2}\ |\beta \|_{2}^{2}\right\},}$

co jest równoważne rozwiązaniu

${\ Displaystyle {\ rozpocząć {wyrównane} \ min _ {\ beta _ {0}, \ beta} \ lewo \ {\ lewo \ | y- \ beta _ {0} -X \ beta \ prawo \ | _ {2 }^{2}\right\}&{\text{ podlega }}(1-\alpha )\|\beta \|_{1}+\alpha \|\beta \|_{2}^{2 }\leq t,\\&{\text{ gdzie }}\alpha ={\frac {\lambda _{2}}{\lambda _{1}+\lambda _{2}}}.\end{wyrównane }}}$

Problem ten można zapisać w prostej formie lassa

${\ Displaystyle \ min _ {\ beta ^ {*} \ w \ mathbb {R} ^ {p }}\left\{\left\|y^{*}-X^{*}\beta ^{*}\right\|_{2}^{2}+\lambda ^{*}\|\beta ^{*}\|_{1}\prawo\}}$

pozwalać

${\ Displaystyle X_ {(n + p) \ razy p} ^ {*} =(1+\lambda _{2})^{-1/2}{\binom {X}{\lambda _{2}^{1/2}I_{p\razy p}}}}$ , ${\ Displaystyle y_ {(n + p)} ^ {*} = {\ binom {y} {0 ^ {p}}}, \ qquad \ lambda ^ {*} = {\ frac {\ lambda _ {1}}{\ sqrt {1+ \ lambda _ {2}}}}}$ , ${\ Displaystyle \ beta ^ {*} = {\ sqrt {1+ \ lambda _ {2}}} \ beta.}$

β ${\ Displaystyle {\ kapelusz {\ beta}} = {\ Frac {{\ kapelusz {\ beta}} ^ {*}} {\ sqrt {1+ \ lambda _$ , co daje, gdy współzmienne są ortogonalne względem siebie

${\ Displaystyle {\ kapelusz {\ beta}} _ {j} = {\ Frac {{\ kapelusz {\ beta}} _ {j} ^ {\ tekst {*, OLS}}} {\ sqrt {1+ \ lambda _{2}}}}\max \left(0,1-{\frac {\lambda ^{*}}{\left|{\hat {\beta}}_{j}^{\text{* ,OLS}}\right|}}\right)={\frac {{\hat {\beta}}_{j}^{\text{OLS}}}{1+\lambda _{2}}}\ max \left(0,1-{\frac {\lambda _{1}}{\left|{\hat {\beta}}_{j}^{\text{OLS}}\right|}}\right )=(1+\lambda _{2})^{-1}{\kapelusz {\beta}}_{j}^{\text{lasso}}.}$

Tak więc wynik kary za siatkę elastyczną jest kombinacją efektów kar za lasso i kar za grzbiet.

Wracając do przypadku ogólnego, fakt, że funkcja kary jest teraz ściśle wypukła oznacza, że ​​jeśli ${\ Displaystyle x_ {(j)} = x_ {(k)}}$ , ${\ Displaystyle {\ kapelusz {\ beta}} _ {j} = {\ kapelusz {\ beta}} _ {k}}$ , co jest zmianą w stosunku do lassa. Ogólnie rzecz biorąc, jeśli ${\ Displaystyle {\ kapelusz {\ beta}} _ {j} {\ kapelusz {\ beta _ {k}}}> 0}$

${\ Displaystyle {\ Frac {| {\ kapelusz {\ beta}} _ {j} - {\ kapelusz {\ beta _{k}}}|}{\|y\|}}\równoważnik \lambda _{2}^{-1}{\sqrt {2(1-\rho _{jk})}},{\ tekst{ gdzie }}\rho =X^{t}X,}$

$.$ jest przykładową macierzą korelacji, ponieważ są znormalizowane

Dlatego wysoce skorelowane zmienne towarzyszące mają zwykle podobne współczynniki regresji, przy czym stopień podobieństwa zależy zarówno od ${\ Displaystyle \|y \|_ {1}},$ jak i ${\ Displaystyle \ lambda _ {2}}$ , co różni się od lassa. Zjawisko to, w którym silnie skorelowane współzmienne mają podobne współczynniki regresji, nazywane jest efektem grupowania. Grupowanie jest pożądane, ponieważ w zastosowaniach takich jak wiązanie genów z chorobą preferowane jest znalezienie wszystkich powiązanych zmiennych towarzyszących, zamiast wybierania jednej z każdego zestawu skorelowanych zmiennych towarzyszących, jak często robi to lasso. Ponadto wybranie tylko jednego z każdej grupy zwykle skutkuje zwiększonym błędem prognozy, ponieważ model jest mniej niezawodny (dlatego regresja grzbietu często przewyższa lasso).

Lasso grupowe

W 2006 roku Yuan i Lin wprowadzili lasso grupowe, aby umożliwić wspólne wybieranie predefiniowanych grup współzmiennych do lub z modelu. Jest to przydatne w wielu ustawieniach, być może najbardziej oczywiste, gdy zmienna kategorialna jest zakodowana jako zbiór współzmiennych binarnych. W takim przypadku grupowe lasso może zapewnić, że wszystkie zmienne kodujące współzmienną jakościową zostaną razem uwzględnione lub wykluczone. Innym środowiskiem, w którym grupowanie jest naturalne, są badania biologiczne. Ponieważ geny i białka często leżą w znanych szlakach, to, które szlaki są powiązane z wynikiem, może być bardziej znaczące niż to, czy poszczególne geny są. Funkcja celu dla lassa grupowego jest naturalnym uogólnieniem standardowego celu lassa

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {\ lewo \ | y- \ suma _ {j = 1} ^ {J} X_ {j} \ beta _ {j}\right\|_{2}^{2}+\lambda \sum _{j=1}^{J}\|\beta _{j}\|_{K_{j}}\right\ },\qquad \|z\|_{K_{j}}=(z^{t}K_{j}z)^{1/2}}$

gdzie macierz projektu i wektor współzmiennych ${j}}$ zastąpione zbiorem macierzy projektu i wektorów współzmiennych $X$$X_ {$$}$$Displaystyle$ , po jednym dla każdej z grup J. Dodatkowo, termin kary $j}}$ teraz sumą norm określonych przez dodatnio określone macierze. $jot {\ Displaystyle$ . Jeśli każda współzmienna jest w swojej własnej grupie i $I }$ to sprowadza się to do standardowego lassa, podczas gdy jeśli jest tylko jedna grupa i $1}=I}$$\ displaystyle K_ {$ , redukuje się do regresji grzbietu. Ponieważ kara zmniejsza się do ${\ Displaystyle \ ell ^ {2}}$ normą w podprzestrzeniach zdefiniowanych przez każdą grupę, nie może wybrać tylko niektórych współzmiennych z grupy, tak jak nie może tego zrobić regresja grzbietowa. Jednakże, ponieważ kara jest sumą różnych norm podprzestrzennych, jak w standardowym lasso, ograniczenie ma pewne punkty niezróżnicowane, które odpowiadają niektórym podprzestrzeniom identycznym zeru. Dlatego może ustawić wektory współczynników odpowiadające niektórym podprzestrzeniom na zero, podczas gdy inne tylko zmniejszają. Możliwe jest jednak rozszerzenie lassa grupowego do tak zwanego rzadkiego lassa grupowego, które może wybierać poszczególne zmienne towarzyszące w grupie, dodając dodatkowe ${\ displaystyle \ ell ^ {1}}$ kara dla każdej podprzestrzeni grupy. Inne rozszerzenie, grupowe lasso z nakładaniem się, umożliwia współdzielenie współzmiennych między grupami, np. jeśli gen miałby wystąpić w dwóch szlakach.

Połączone lasso

W niektórych przypadkach badane zjawisko może mieć ważną strukturę przestrzenną lub czasową, którą należy wziąć pod uwagę podczas analizy, na przykład szeregi czasowe lub dane obrazowe. W 2005 roku Tibshirani i współpracownicy wprowadzili połączone lasso, aby rozszerzyć użycie lassa na tego typu dane. Skondensowana funkcja celu lassa to

${\ Displaystyle {\ rozpocząć {wyrównane} & \ min _ {\ beta} \ lewo \ {{\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} \ lewo (y_ {i} -x_{i}^{t}\beta \right)^{2}\right\}\\[4pt]&{\text{ temat }}\sum _{j=1}^{p}|\ beta _{j}|\równik t_{1}{\text{ i }}\suma _{j=2}^{p}|\beta _{j}-\beta _{j-1}|\rów t_{2}.\end{wyrównane}}}$

Pierwszym ograniczeniem jest ograniczenie lassa, podczas gdy drugie bezpośrednio karze duże zmiany w odniesieniu do struktury czasowej lub przestrzennej, co wymusza płynną zmianę współczynników w celu odzwierciedlenia podstawowej logiki systemu. Klastrowe lasso to uogólnienie połączonego lassa, które identyfikuje i grupuje odpowiednie zmienne towarzyszące na podstawie ich efektów (współczynników). Podstawową ideą jest karanie różnic między współczynnikami, tak aby niezerowe skupiały się. Można to modelować za pomocą następującej regularyzacji:

${\ Displaystyle \ suma _ {i <j} ^ {p} | \ beta _ {i} - \ beta _ {j} | \ równoważnik t_ {2}.}$

W przeciwieństwie do tego, zmienne można grupować w wysoce skorelowane grupy, a następnie z każdego skupienia można wyodrębnić pojedynczą reprezentatywną współzmienną.

Istnieją algorytmy, które rozwiązują problem połączonego lassa i niektóre jego uogólnienia. Algorytmy mogą rozwiązać go dokładnie w skończonej liczbie operacji.

Quasi-normy i regresja pomostowa

Przykład funkcji potencjalnej PQSQ (kawałkowa funkcja kwadratowa wzrostu subkwadratowego) ${\ Displaystyle u (x)}$ ; tutaj główną funkcją jest ${\ Displaystyle f (x) = x}$ ; potencjał jest definiowany za pomocą przycinania po ${\ displaystyle r_ {3}}$ .

Przykład, jak wydajna regularna regresja PQSQ działa tak samo $jak$ .

norms ($konieczne$ i połączone lasso konstruują funkcje karne z $)$ (z wagami, jeśli to Regresja pomostowa wykorzystuje ogólne $0<p<1$$i$ quasinormy ( $displaystyle$). For example, for p =1/2 odpowiednikiem celu lassa w postaci Lagrange'a jest rozwiązanie

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {{\frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda {\sqrt {\|\beta \|_{1/2}} }\Prawidłowy\},}$

Gdzie

${\ Displaystyle \|\ beta \|_ {1/2} = \ lewo (\ suma _ {j = 1} ^ {p} {\sqrt {|\beta _{j}|}}\right)^{2}}$

$dostarczają$ się, że ułamkowe quasi-normy $bardziej$ wyników w analizie danych, zarówno teoretycznie, jak empirycznie Brak wypukłości tych quasi-norm komplikuje problem optymalizacji. Aby rozwiązać ten problem, opracowano i wdrożono procedurę minimalizacji oczekiwań w celu minimalizacji funkcji

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p }}\left\{{\frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda \sum _{j=1}^{p} \vartheta (\beta _{j}^{2})\right\},}$

gdzie ${\ Displaystyle \ vartheta (\ gamma)}$ jest dowolną wklęsłą monotonicznie rosnącą funkcją (na przykład ${\ Displaystyle \ vartheta (\ gamma) = {\ sqrt {\ gamma}} }$$}$ karę lasso i / $\$ kara).

Wydajny algorytm minimalizacji opiera się na kwadratowej aproksymacji subkwadratowego wzrostu (PQSQ).

Lasso adaptacyjne

Adaptacyjne lasso zostało wprowadzone przez Zou w 2006 r. do regresji liniowej oraz przez Zhanga i Lu w 2007 r. do regresji proporcjonalnego hazardu.

Wcześniejsze lasso

Wcześniejsze lasso zostało wprowadzone do uogólnionych modeli liniowych przez Jianga i in. w 2016 r. w celu uwzględnienia wcześniejszych informacji, takich jak znaczenie niektórych zmiennych towarzyszących. We wcześniejszym lasso takie informacje są podsumowywane w pseudoodpowiedziach (zwanych wcześniejszymi odpowiedziami), $następnie do zwykłego$ dodaje się dodatkową funkcję funkcja z karą lassa. Bez utraty ogólności, w regresji liniowej nową funkcję celu można zapisać jako

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ lewo \ {{\ Frac {1} {N}} \ lewo \ | yX \ beta \ prawo \ |_ {2} ^{2}+{\frac {1}{N}}\eta \left\|{\hat {y}}^{\mathrm {p}}-X\beta \right\|_{2}^{ 2}+\lambda \|\beta \|_{1}\right\},}$

co jest równoważne

${\ Displaystyle \ min _ {\ beta \ w \ mathbb {R} ^ {p}} \ left\{{\frac {1}{N}}\left\|{\tylda {y}}-X\beta \right\|_{2}^{2}+{\frac {\lambda}}{1 +\eta }}\|\beta \|_{1}\right\},}$

$y$ z odpowiedziami zastępowanymi przez średnią ważoną obserwowanych odpowiedzi i wcześniejszych odpowiedzi $\ displaystyle {\ tylda {y}}=(y+\eta {\hat {y}}^{\mathrm {p}})/(1+\eta)} (nazywane skorygowanymi wartościami$ odpowiedzi przez wcześniejsze informacje).

$lasso$ parametr jest parametrem równoważącym, ponieważ równoważy względne znaczenie danych i wcześniejszych informacji. W $lasso$ przypadku jest redukowane do lassa. Jeśli ${\ displaystyle \ eta = \ infty}$ , wcześniejsze lasso będzie polegać wyłącznie na wcześniejszych informacjach, aby dopasować model. Ponadto parametr równoważący ma inną atrakcyjną interpretację: kontroluje wariancję ${\ displaystyle \ eta}$${\ displaystyle \ beta}$ w swojej wcześniejszej dystrybucji z bayesowskiego punktu widzenia.

Wcześniejsze lasso jest bardziej wydajne w szacowaniu i przewidywaniu parametrów (z mniejszym błędem oszacowania i błędem prognozy), gdy wcześniejsze informacje są wysokiej jakości i są odporne na wcześniejsze informacje niskiej jakości przy dobrym wyborze parametru równoważącego η { $displaystyle \eta}$ .

Obliczeniowe rozwiązania lassowe

Główny artykuł: Proksymalne metody gradientowe do uczenia się § Regularyzacja Lasso

Funkcja strat lassa nie jest różniczkowalna, ale opracowano szeroką gamę technik z analizy wypukłej i teorii optymalizacji w celu obliczenia ścieżki rozwiązania lassa. Obejmują one zejście współrzędnych, metody subgradientowe, regresję najmniejszego kąta (LARS) i metody proksymalnego gradientu. Metody subgradientowe są naturalnym uogólnieniem tradycyjnych metod, takich jak zejście gradientowe i stochastyczne zejście gradientowe do przypadku, w którym funkcja celu nie jest różniczkowalna we wszystkich punktach. LARS to metoda, która jest ściśle powiązana z modelami lassa iw wielu przypadkach pozwala na ich efektywne dopasowanie, chociaż może nie działać dobrze we wszystkich okolicznościach. LARS generuje kompletne ścieżki rozwiązań. Metody proksymalne stały się popularne ze względu na ich elastyczność i wydajność i są obszarem aktywnych badań. Wybór metody będzie zależał od konkretnego wariantu lassa, danych i dostępnych zasobów. Jednak metody proksymalne generalnie działają dobrze.

Wybór parametru regularyzacji

Wybór parametru regularyzacji ( $.$ jest podstawową częścią lassa Dobra wartość jest niezbędna do wykonania lassa, ponieważ kontroluje siłę skurczu i wybór zmiennych, co z umiarem może poprawić zarówno dokładność przewidywania, jak i interpretację. Jeśli jednak regularyzacja stanie się zbyt silna, ważne zmienne mogą zostać pominięte, a współczynniki mogą zostać nadmiernie zmniejszone, co może zaszkodzić zarówno zdolności predykcyjnej, jak i wnioskowaniu. Walidacja krzyżowa jest często używana do znalezienia parametru regularyzacji.

Kryteria informacyjne, takie jak Bayesowskie kryterium informacyjne (BIC) i kryterium informacyjne Akaike (AIC) mogą być lepsze niż walidacja krzyżowa, ponieważ są szybsze w obliczeniach, a ich wydajność jest mniej zmienna w małych próbkach. Kryterium informacyjne wybiera parametr regularyzacji estymatora, maksymalizując dokładność modelu w próbie, jednocześnie karając jego efektywną liczbę parametrów / stopni swobody. Zou i in. zaproponowano pomiar efektywnych stopni swobody przez zliczenie liczby parametrów, które odbiegają od zera. Podejście oparte na stopniach swobody zostało uznane za wadliwe przez Kaufmana i Rosseta oraz Jansona i in., ponieważ stopnie swobody modelu mogą wzrosnąć, nawet jeśli jest on bardziej karany przez parametr regularyzacji. Alternatywnie, zdefiniowana powyżej miara względnej prostoty może być wykorzystana do obliczenia efektywnej liczby parametrów. W przypadku lassa miara ta jest dana przez

${\ Displaystyle {\ kapelusz {\ mathcal {P}}} = \ suma _ {i = 1} ^ {p} {\ Frac {|\ beta _ {i} - \ beta _ {0, i} |} { {\frac {1}{p}}\sum _{l}|b_{OLS,l}-\beta _{0,l}|}}}$ ,

$wzrasta$ od zera do $gdy$ parametr regularyzacji spada od do zera.

Wybrane aplikacje

LASSO zostało zastosowane w ekonomii i finansach i okazało się, że poprawia przewidywania i wybiera czasami zaniedbywane zmienne, na przykład w literaturze dotyczącej przewidywania upadłości przedsiębiorstw lub przewidywaniach firm o wysokim wzroście.

Zobacz też

• Najmniejsze odchylenia bezwzględne
• Wybór modelu
• Regresja nieparametryczna
• Regularyzacja Tichonowa