Gasnące światła (gra)
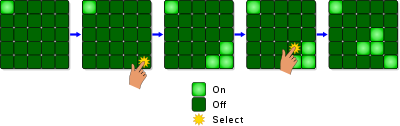
Lights Out to gra elektroniczna wydana przez Tiger Electronics w 1995 roku. Gra składa się z siatki świateł 5 na 5. Po rozpoczęciu gry zapala się losowa liczba lub zapisany wzór tych świateł. Naciśnięcie dowolnego światła spowoduje przełączenie go i sąsiednich świateł. Celem układanki jest wyłączenie wszystkich świateł, najlepiej przy jak najmniejszej liczbie naciśnięć przycisków.
Merlin , podobna gra elektroniczna, została wydana przez Parker Brothers w latach 70. XX wieku z podobnymi zasadami na siatce 3 na 3. Kolejna podobna gra została wyprodukowana przez firmę Vulcan Electronics w 1983 roku pod nazwą XL-25 . Tiger Toys wyprodukował również kasetową wersję Lights Out na swoją przenośną konsolę do gier Game com w 1997 roku, dostarczaną bezpłatnie z konsolą.
Wydano wiele nowych łamigłówek podobnych do Lights Out , takich jak Lights Out 2000 (5×5 z wieloma kolorami), Lights Out Cube (sześć ścian 3×3 z efektami na krawędziach) i Lights Out Deluxe (6×6 ).
wynalazcy
Lights Out zostało stworzone przez grupę ludzi, w tym Avi Olti, Gyora Benedek, Zvi Herman, Revital Bloomberg, Avi Weiner i Michael Ganor. Członkowie grupy razem i indywidualnie wymyślili także kilka innych gier, takich jak Hidato , NimX, iTop i wiele innych.
Rozgrywka
Gra składa się z siatki świateł 5 na 5. Po rozpoczęciu gry zapala się losowa liczba lub zapisany wzór tych świateł. Naciśnięcie dowolnego światła spowoduje przełączenie go i czterech sąsiednich świateł. Celem układanki jest wyłączenie wszystkich świateł, najlepiej za pomocą jak najmniejszej liczby naciśnięć przycisków.
Matematyka
Jeśli światło jest włączone, należy je przełączyć nieparzystą liczbę razy, aby zostało wyłączone. Jeśli światło jest wyłączone, musi zostać przełączone parzystą liczbę razy (w tym wcale), aby pozostało wyłączone. Do strategii gry wykorzystano kilka wniosków. Po pierwsze, kolejność wciskania świateł nie ma znaczenia, ponieważ efekt będzie taki sam. Po drugie, w rozwiązaniu minimalnym każdą lampkę trzeba nacisnąć nie więcej niż raz, ponieważ dwukrotne naciśnięcie lampki jest równoznaczne z całkowitym jej brakiem.
W 1998 roku Marlow Anderson i Todd Feil użyli algebry liniowej, aby udowodnić, że nie wszystkie konfiguracje są rozwiązywalne, a także, aby udowodnić, że istnieją dokładnie cztery zwycięskie scenariusze, nie licząc zbędnych ruchów, dla każdego rozwiązalnego problemu 5 × 5. Siatkę 5×5 Lights Out można przedstawić jako wektor kolumnowy 25x1 z 1 i 0 oznaczającymi odpowiednio światło w stanie włączonym i wyłączonym. Każdy wpis jest elementem Z 2 , pola liczb całkowitych modulo 2. Anderson i Feil stwierdzili, że aby konfiguracja była rozwiązywalna (wyprowadzając wektor zerowy z pierwotnej konfiguracji), musi być ortogonalna do dwóch wektorów N 1 i N 2 poniżej (przedstawiony jako tablica 5 × 5, ale nie mylić z macierzami).
Ponadto odkryli, że N 1 i N 2 można wykorzystać do znalezienia trzech dodatkowych rozwiązań z rozwiązania i że te cztery rozwiązania są jedynymi czterema rozwiązaniami (z wyłączeniem zbędnych ruchów) początkowej danej konfiguracji. Te cztery rozwiązania to X, X + N 1 , X + N 2 i X + N 1 + N 2 , gdzie X jest rozwiązaniem początkowej danej konfiguracji. Wprowadzenie do tej metody opublikował Robert Eisele.
Lekka pogoń
„Ściganie światła” to metoda podobna do eliminacji Gaussa , która zawsze rozwiązuje zagadkę (jeśli rozwiązanie istnieje), chociaż z możliwością wielu zbędnych kroków. W tym podejściu wiersze są manipulowane pojedynczo, zaczynając od górnego rzędu. Wszystkie światła są wyłączane w rzędzie, przełączając sąsiednie światła w rzędzie bezpośrednio poniżej. Ta sama metoda jest następnie stosowana w kolejnych rzędach aż do ostatniego. Ostatni rząd jest rozwiązywany osobno, w zależności od aktywnych świateł. Odpowiednie światła (patrz tabela poniżej) w górnym rzędzie są przełączane i ponownie uruchamiany jest początkowy algorytm, co daje rozwiązanie.
| Dolny rząd jest | Przełącz w górnym rzędzie |
|---|---|
| ⬜⬜⬜⬛⬛ | ⬛▣⬛⬛⬛ |
| ⬜⬜⬛⬜⬜ | ⬛⬛▣⬛⬛ |
| ⬜⬛⬜⬜⬛ | ⬛⬛⬛⬛▣ |
| ⬜⬛⬛⬛⬜ | ▣▣⬛⬛⬛ |
| ⬛⬜⬜⬛⬜ | ▣⬛⬛⬛⬛ |
| ⬛⬜⬛⬜⬛ | ▣⬛⬛▣⬛ |
| ⬛⬛⬜⬜⬜ | ⬛⬛⬛▣⬛ |
Tabele i strategie dla innych rozmiarów planszy są generowane przez grę Lights Out z pustą planszą i obserwowanie wyniku przeniesienia określonego światła z górnego rzędu do dolnego.
Dalsze wyniki
Po znalezieniu pojedynczego rozwiązania rozwiązanie z minimalną liczbą ruchów można określić poprzez wyeliminowanie zbędnych zestawów naciśnięć przycisków, które nie mają skumulowanego efektu. Jeśli łamigłówki 5 × 5 nie da się rozwiązać w ramach legalnej gry, dwa skrajne lewe światła w dolnym rzędzie pozostaną włączone, gdy wszystkie inne światła zostaną wyłączone.
Udowodniono istnienie rozwiązań dla szerokiej gamy konfiguracji plansz, takich jak sześciokątne, podczas gdy rozwiązania dla tablic n na n dla n≤200 zostały wyraźnie skonstruowane.
Istnieje rozwiązanie dla każdego przypadku N×N. Można go rozwiązać na dowolnym grafie nieskierowanym, w którym kliknięcie jednego wierzchołka odwraca jego wartość i sąsiadów. Mówiąc bardziej ogólnie, jeśli macierz akcji jest symetryczna, to jej przekątna jest zawsze rozwiązywalna.