Maszerujące kwadraty

W grafice komputerowej maszerujące kwadraty to algorytm generujący kontury dla dwuwymiarowego pola skalarnego (prostokątnej tablicy pojedynczych wartości liczbowych). Podobną metodę można zastosować do konturowania siatek trójkątów 2D .

Kontury mogą być dwojakiego rodzaju:

  • Izolinie – linie następujące po jednym poziomie danych lub izowartość .
  • Izopasma – wypełnione obszary między izoliniami.

Typowe zastosowania obejmują linie konturowe na mapach topograficznych lub generowanie izobar na mapach pogodowych .

Marszowe kwadraty mają podobne podejście do algorytmu maszerujących kostek 3D :

  • Przetwarzaj każdą komórkę w siatce niezależnie.
  • Oblicz indeks komórki, porównując poziom (poziomy) konturu z wartościami danych w rogach komórki.
  • Użyj gotowej tabeli przeglądowej , wpisanej na podstawie indeksu komórki, aby opisać wyjściową geometrię komórki.
  • Zastosuj interpolację liniową wzdłuż granic komórki, aby obliczyć dokładne położenie konturu.

Podstawowy algorytm

Oto kroki algorytmu:

Zastosuj próg do pola 2D, aby utworzyć obraz binarny zawierający:

  • 1, gdzie wartość danych jest powyżej izowartości
  • 0, gdzie wartość danych jest poniżej izowartości

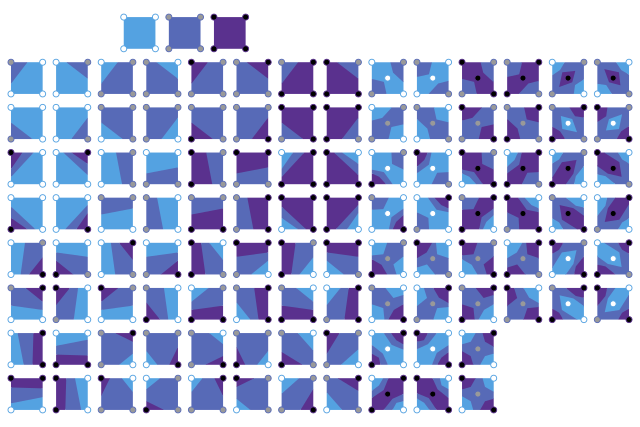
Każdy blok pikseli 2x2 w obrazie binarnym tworzy komórkę konturową, więc cały obraz jest reprezentowany przez siatkę takich komórek (pokazaną na zielono na poniższym obrazku). Należy zauważyć, że ta siatka konturowa jest o jedną komórkę mniejsza w każdym kierunku niż oryginalne pole 2D.

Dla każdej komórki w siatce konturowej:

  1. Skomponuj 4 bity w rogach komórki, aby zbudować indeks binarny: obejdź komórkę w kierunku zgodnym z ruchem wskazówek zegara , dodając bit do indeksu, używając bitowego OR i przesunięcia w lewo , od najbardziej znaczącego bitu w lewym górnym rogu do najmniejszego znaczący bit w lewym dolnym rogu. Wynikowy 4-bitowy indeks może mieć 16 możliwych wartości z zakresu 0–15.
  2. Użyj indeksu komórki, aby uzyskać dostęp do gotowej tabeli przeglądowej z 16 wpisami zawierającymi krawędzie potrzebne do reprezentowania komórki (pokazane w prawej dolnej części poniższego rysunku).
  3. Zastosuj interpolację liniową między oryginalnymi wartościami danych pola, aby znaleźć dokładne położenie linii konturu wzdłuż krawędzi komórki.

Marching Squares Algorithm illustration.

Ujednoznacznienie punktów siodłowych

Kontur jest niejednoznaczny w punktach siodłowych . Możliwe jest rozwiązanie niejednoznaczności, używając średniej wartości danych dla środka komórki, aby wybrać między różnymi połączeniami interpolowanych punktów (cztery obrazy w prawym dolnym rogu):

Marching squares

izobandy

Podobny algorytm można stworzyć dla wypełnionych pasm konturowych w obrębie górnych i dolnych wartości progowych:

Marching squares in the isoband case

Konturowanie siatek trójkątów

Ten sam podstawowy algorytm można zastosować do siatek trójkątnych , które składają się z połączonych trójkątów z danymi przypisanymi do wierzchołków. Na przykład rozproszony zestaw punktów danych można połączyć z triangulacją Delaunaya , aby umożliwić obrysowanie pola danych.

Komórka trójkątna jest zawsze planarna , ponieważ jest 2-simplexem (tj. określona przez n +1 wierzchołków w n -wymiarowej przestrzeni). Zawsze istnieje unikalny liniowy interpolant w poprzek trójkąta i nie ma możliwości niejednoznacznego siodełka.

izolinie

Analiza izolinii na trójkątach jest szczególnie prosta: są 3 cyfry binarne, więc jest 8 możliwości:

Marching triangles cases, isoline case

izobandy

Analiza izopasm nad trójkątami wymaga 3 trytów trójskładnikowych, więc jest 27 możliwości:

Marching triangles cases, isoband case

Wymiary i przestrzenie

Przestrzeń danych dla algorytmu Marching Squares jest dwuwymiarowa, ponieważ wierzchołki, którym przypisano wartość danych, są połączone z sąsiadami w siatce topologicznej 2D , ale współrzędne przestrzenne przypisane do wierzchołków mogą mieć wymiary 2D, 3D lub wyższe.

Na przykład trójkątna siatka może reprezentować powierzchnię danych 2D osadzoną w przestrzeni 3D, gdzie przestrzenne pozycje wierzchołków i punktów interpolowanych wzdłuż konturu będą miały wszystkie 3 współrzędne. Zauważ, że przypadek kwadratów jest znowu niejednoznaczny, ponieważ czworobok osadzony w przestrzeni trójwymiarowej niekoniecznie jest płaski, więc istnieje wybór schematu interpolacji geometrycznej do rysowania pasmowych powierzchni w 3D.

Względy dotyczące wydajności

Algorytm jest żenująco równoległy , ponieważ wszystkie komórki są przetwarzane niezależnie. Łatwo jest napisać algorytm równoległy, zakładając, że:

  • Współdzielone wejściowe pole skalarne tylko do odczytu.
  • Udostępniony strumień wyjściowy geometrii tylko do dołączania.

Naiwna implementacja Marching Squares, która niezależnie przetwarza każdą komórkę, wykona każdą interpolację liniową dwa razy (izolinia) lub cztery razy (izopasmo). Podobnie wynik będzie zawierał 2 kopie wierzchołków 2D dla linii rozłącznych (izolinii) lub 4 kopie dla wielokątów (izopasm). [Przy założeniu, że: siatka jest duża, więc większość komórek jest wewnętrzna; i tworzony jest pełny ciągły zestaw izopasm.]

Możliwe jest zmniejszenie narzutu obliczeniowego poprzez buforowanie wyników interpolacji. Na przykład jednowątkowa wersja szeregowa musiałaby buforować tylko interpolowane wyniki dla jednego wiersza siatki wejściowej.

Możliwe jest również zmniejszenie rozmiaru danych wyjściowych za pomocą indeksowanych prymitywów geometrycznych, tj. utworzenie tablicy wierzchołków 2D i określenie linii lub wielokątów z krótkimi przesunięciami całkowitymi w tablicy.

  •   Klon, C. (2003). Projektowanie geometryczne i planowanie przestrzenne z wykorzystaniem algorytmów maszerujących kwadratów i sześcianów marszowych . proc. 2003 Międzynarodowy konf. Modelowanie geometryczne i grafika . s. 90–95. doi : 10.1109/GMAG.2003.1219671 . ISBN 978-0-7695-1985-2 .
  •    Banki, DC (2004). „Zliczanie przypadków w algorytmach substitopowych”. IEEE Trans. Wizualny. Komp. Grafika . 10 (4): 371–384. CiteSeerX 10.1.1.582.7221 . doi : 10.1109/TVCG.2004.6 . PMID 18579966 .
  • Laguardia, JJ; Cueto, E.; Doblaré, M. (2005). „Metoda naturalnego sąsiada Galerkina ze strukturą drzewa czworokątnego”. Int. J. Numer. Metody inż . 63 (6): 789–812. Bibcode : 2005IJNME..63..789L . doi : 10.1002/nme.1297 .
  • Schaefer, Scott; Warren, Joe (2005). „Podwójne sześciany marszowe: pierwotne konturowanie podwójnych siatek”. Forum grafiki komputerowej . 24 (2): 195–201. doi : 10.1111/j.1467-8659.2005.00843.x .
  • Mantz, Huber; Jacobs, Karin; Mecke, Klaus (2008). „Wykorzystanie funkcjonałów Minkowskiego do analizy obrazu: algorytm maszerującego kwadratu”. J. Stat. Mech.: Teoria Eksp . 2008 (12): P12015. Bibcode : 2008JSMTE..12..015M . doi : 10.1088/1742-5468/2008/12/P12015 .
  • Cipolletti, Marina P.; Delrieux, Claudio A.; Perillo, Gerardo ME; Piccolo, M. Cintia (2012). „Segmentacja granic superrozdzielczości i pomiar w obrazach teledetekcyjnych”. Komp. Geologia . 40 : 87–97. Bibcode : 2012CG.....40...87C . doi : 10.1016/j.cageo.2011.07.015 .

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Marching_squares&oldid=1114334835 ”