Model kamery otworkowej
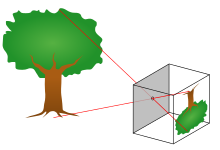
Model kamery otworkowej opisuje matematyczną zależność między współrzędnymi punktu w przestrzeni trójwymiarowej a jego rzutem na płaszczyznę obrazu idealnej kamery otworkowej , w której apertura kamery jest opisana jako punkt i żadne soczewki nie są używane do skupiania światła. W modelu nie uwzględniono np. zniekształceń geometrycznych czy rozmycia obiektów nieostrych spowodowanych przez soczewki i przysłony o skończonych rozmiarach. Nie bierze również pod uwagę, że większość praktycznych aparatów ma tylko dyskretne współrzędne obrazu. Oznacza to, że model kamery otworkowej może być używany tylko jako przybliżenie pierwszego rzędu odwzorowania z a sceny 3D na obraz 2D . Jego ważność zależy od jakości aparatu i ogólnie zmniejsza się od środka obrazu do krawędzi wraz ze wzrostem zniekształceń obiektywu.
Niektóre efekty, których model kamery otworkowej nie bierze pod uwagę, można skompensować, na przykład stosując odpowiednie przekształcenia współrzędnych współrzędnych obrazu; inne efekty są na tyle małe, że można je pominąć, jeśli używany jest aparat wysokiej jakości. Oznacza to, że model kamery otworkowej często może być używany jako rozsądny opis sposobu, w jaki kamera przedstawia scenę 3D, na przykład w wizji komputerowej i grafice komputerowej .
Geometria
Geometria związana z mapowaniem kamery otworkowej jest przedstawiona na rysunku. Rysunek zawiera następujące podstawowe obiekty:
- Ortogonalny układ współrzędnych 3D z początkiem w punkcie O . Tam też znajduje się przysłona aparatu . Trzy osie układu współrzędnych są określane jako X1, X2, X3. Oś X3 jest skierowana w kierunku patrzenia kamery i jest nazywana osią optyczną , osią główną lub promieniem głównym . Płaszczyzna rozpięta przez osie X1 i X2 to przednia strona kamery, czyli płaszczyzna główna .
- Płaszczyzna obrazu, na której świat 3D jest rzutowany przez aperturę aparatu. Płaszczyzna obrazu jest równoległa do osi X1 i X2 i znajduje się w odległości od początku w ujemnym kierunku osi X3, gdzie f jest ogniskową kamery otworkowej Praktyczna implementacja kamery otworkowej oznacza, że płaszczyzna obrazu jest umieszczona w taki sposób, że przecina oś X3 na współrzędnej -f, gdzie f > 0 .
- Punkt R na przecięciu osi optycznej i płaszczyzny obrazu. Punkt ten nazywany jest punktem głównym lub środkiem obrazu .
- Punkt P świecie osi
- Linia rzutowania punktu P na kamerę. To jest zielona linia, która przechodzi przez punkt P i punkt O.
- Rzut punktu P na płaszczyznę obrazu, oznaczony jako Q . Punkt ten wyznacza przecięcie linii projekcji (kolor zielony) i płaszczyzny obrazu. W każdej praktycznej sytuacji możemy założyć, że > 0 which means that the intersection point is well defined.
- Na płaszczyźnie obrazu istnieje również układ współrzędnych 2D, którego początek znajduje się w R , a osie Y1 i Y2 są równoległe odpowiednio do X1 i X2. Współrzędne punktu Q względem tego układu współrzędnych to .
otwór otworkowy kamery, przez który muszą przechodzić wszystkie linie projekcji, jest nieskończenie mały, punkt. W literaturze ten punkt w przestrzeni 3D jest określany jako środek optyczny (lub obiektywu lub kamery) .
Sformułowanie
Następnie chcemy zrozumieć, w jaki sposób współrzędne zależą od współrzędnych punktu P . Można to zrobić za pomocą poniższego rysunku, który pokazuje tę samą scenę co poprzedni rysunek, ale teraz z góry, patrząc w dół w ujemnym kierunku osi X2.
Na tym rysunku widzimy dwa podobne trójkąty , z których oba mają części linii projekcji (zielona) jako przeciwprostokątne . Catheti lewego trójkąta to a catheti prawego trójkąta to i 1 {\ i Displaystyle x_ . Wynika z tego, że oba trójkąty są podobne
- lub
Podobne badanie, patrząc w kierunku ujemnym osi X1 daje
- lub
Można to podsumować jako
które jest wyrażeniem opisującym zależność między współrzędnymi 3D punktu P a współrzędnymi jego obrazu podane przez punkt Q na płaszczyźnie obrazu.
Obrócony obraz i wirtualna płaszczyzna obrazu
Mapowanie ze współrzędnych 3D na 2D opisane przez kamerę otworkową to projekcja perspektywiczna , po której następuje obrót o 180° w płaszczyźnie obrazu. Odpowiada to działaniu prawdziwej kamery otworkowej; wynikowy obraz jest obracany o 180°, a względny rozmiar rzutowanych obiektów zależy od ich odległości od ogniska, a całkowity rozmiar obrazu zależy od odległości f między płaszczyzną obrazu a ogniskiem. Aby uzyskać nieobrócony obraz, czego oczekujemy od aparatu, istnieją dwie możliwości:
- Obróć układ współrzędnych na płaszczyźnie obrazu o 180° (w dowolnym kierunku). W ten sposób każda praktyczna implementacja kamery otworkowej rozwiązałaby problem; w przypadku aparatu fotograficznego obracamy obraz przed spojrzeniem na niego, aw przypadku aparatu cyfrowego odczytujemy piksele w takiej kolejności, aby został on obrócony.
- Umieść płaszczyznę obrazu tak, aby przecinała oś X3 w punkcie f zamiast w -f i przerób poprzednie obliczenia. To wygenerowałoby wirtualną (lub przednią) płaszczyznę obrazu , której nie można zaimplementować w praktyce, ale zapewnia teoretyczną kamerę, która może być prostsza do analizy niż prawdziwa.
W obu przypadkach wynikowe odwzorowanie ze współrzędnych 3D na współrzędne obrazu 2D jest określone powyższym wyrażeniem, ale bez negacji, a zatem
W jednorodnych współrzędnych
Odwzorowanie współrzędnych 3D punktów w przestrzeni na współrzędne obrazu 2D może być również reprezentowane we współrzędnych jednorodnych . Niech będzie reprezentacją punktu 3D we jednorodnych (wektor 4-wymiarowy) i niech będzie reprezentacją obrazu tego punktu w aparacie otworkowym (wektor trójwymiarowy). Wtedy zachodzi następująca zależność
gdzie jest kamery , a oznacza równość między elementami przestrzeni . Oznacza to, że lewa i prawa strona są równe do niezerowego mnożenia przez skalar. Konsekwencją tej relacji jest to, że również można postrzegać jako element przestrzeni rzutowej do {\ displaystyle \ mathbf { ; dwie macierze kamer są równoważne, jeśli są równe co do mnożenia przez skalar. Ten opis mapowania kamery otworkowej, jako transformacja liniowa zamiast jako ułamek dwóch wyrażeń liniowych, umożliwia uproszczenie wielu wyprowadzeń relacji między współrzędnymi 3D i [ potrzebne źródło ]
Zobacz też
- Resekcja kamery
- Równanie współliniowości
- Źrenica wejściowa , odpowiednik położenia otworka w stosunku do przestrzeni obiektu w prawdziwym aparacie.
- Źrenica wyjściowa , odpowiednik położenia otworka w stosunku do płaszczyzny obrazu w prawdziwym aparacie.
- Ibn al-Hajtham
- Kamera otworkowa , praktyczna implementacja modelu matematycznego opisanego w tym artykule.
- Soczewka prostoliniowa
Bibliografia
- David A. Forsyth i Jean Ponce (2003). Wizja komputerowa, nowoczesne podejście . Sala Prentice'a. ISBN 0-12-379777-2 .
- Richarda Hartleya i Andrew Zissermana (2003). Geometria wielu widoków w wizji komputerowej . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-54051-8 .
- Bernd Jähne (1997). Praktyczny podręcznik dotyczący przetwarzania obrazu do zastosowań naukowych . Prasa CRC. ISBN 0-8493-8906-2 .
- Linda G. Shapiro i George C. Stockman (2001). Wizja komputerowa . Sala Prentice'a. ISBN 0-13-030796-3 .
- Gang Xu i Zhengyou Zhang (1996). Geometria epipolarna w rozpoznawaniu stereo, ruchu i obiektów . Wydawnictwa Naukowe Kluwer. ISBN 0-7923-4199-6 .



















