Model ośmiu wierzchołków

W mechanice statystycznej model ośmiu wierzchołków jest uogólnieniem modeli lodu (sześć wierzchołków) ; został omówiony przez Sutherlanda oraz Fana i Wu i rozwiązany przez Baxtera w przypadku pola zerowego.

Opis

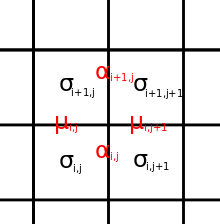
Podobnie jak w przypadku modeli typu lodowego, model z ośmioma wierzchołkami jest modelem sieci kwadratowej , w którym każdy stan jest konfiguracją strzałek na wierzchołku. Dozwolone wierzchołki mają parzystą liczbę strzałek skierowanych w stronę wierzchołka; obejmuje to sześć odziedziczonych po modelu typu lodowego (1-6) oraz pochłaniacze i źródła (7, 8).

osiem wierzchołków2

Rozważamy $i$ z $_$ _ $_$ _ Nałożenie okresowych warunków brzegowych wymaga, aby stany 7 i 8 występowały równie często, jak stany 5 i 6, a zatem można przyjąć, że mają taką samą energię. W przypadku pola zerowego to samo dotyczy dwóch pozostałych par stanów. Każdy wierzchołek ${ \ Displaystyle w_ {j}$$\ frac {\ epsilon _ {j}}{kT}}}}$ energię i wagę Boltzmanna $jot$ , podając funkcję podziału na siatce jako

${\ Displaystyle Z = \ suma \ exp \ lewo (- {\ Frac {\ suma _ {j} n_ {j} \ epsilon _ {j}} {kT}}\prawo)}$

gdzie sumowanie obejmuje wszystkie dozwolone konfiguracje wierzchołków w sieci. W tej ogólnej postaci funkcja podziału pozostaje nierozwiązana.

Rozwiązanie w przypadku pola zerowego

Przypadek pola zerowego w modelu odpowiada fizycznie nieobecności zewnętrznych pól elektrycznych. Stąd model pozostaje niezmieniony przy odwróceniu wszystkich strzałek; w konsekwencji stany 1 i 2 oraz 3 i 4 muszą występować jako pary. Wierzchołkom można przypisać dowolne wagi

${\ Displaystyle {\ rozpocząć {wyrównane} w_ {1} = w_ {2} & = a \\ w_ {3} = w_ {4} & = b \\ w_ {5} = w_ {6} & = c \ \w_{7}=w_{8}&=d.\end{wyrównane}}}$

Rozwiązanie opiera się na obserwacji, że wiersze w macierzach transferowych komutują się, dla pewnej parametryzacji tych czterech wag Boltzmanna. Powstało to jako modyfikacja alternatywnego rozwiązania dla modelu z sześcioma wierzchołkami ; wykorzystuje eliptyczne funkcje theta .

Dojeżdżające macierze transferu

$\ Delta}}$ fakcie, że gdy i dla ilości $=$

$\ Displaystyle {\ rozpocząć {wyrównane} \ Delta & = {\ Frac { a^{2}+b^{2}-c^{2}-d^{2}}{2(ab+cd)}}\\\Gamma &={\frac {ab-cd}{ab+ cd}}\end{wyrównane}}}$

macierze transferu $displaystyle$ ( związane z wagami) $a}$ , ${\ displaystyle b}$$,$ do $\ displaystyle c}$ , $}$ za ${\ Displaystyle a'}$ , ${\ Displaystyle b'}$ , ${\ Displaystyle c'}$ , ${\ Displaystyle d'}$ dojeżdżać. Korzystając z relacji gwiazda-trójkąt , Baxter przeformułował ten warunek jako równoważny parametryzacji wag podanych jako

${\ Displaystyle a: b: c: d = \ nazwa operatora {snh} (\ eta -u): \ nazwa operatora {snh} (\ eta + u): \ nazwa operatora {snh} (2 \ eta): k \ nazwa_operatora {snh} (2\eta )\nazwa_operatora {snh} (\eta -u)\nazwa_operatora {snh} (\eta +u)}$

dla stałego modułu ${\ displaystyle k}$ i zmiennego ${\$$displaystyle \ eta }$ . Tutaj snh jest hiperbolicznym odpowiednikiem sn, podanym przez

${\ Displaystyle {\ rozpocząć {wyrównane }\nazwa_operatora {snh} (u)&=-i\nazwa_operatora {sn} (iu)=i\nazwa_operatora {sn} (-iu)\\{\tekst{gdzie }}\nazwa_operatora {sn} (u)& ={\frac {H(u)}{k^{1/2}\Theta (u)}}\end{wyrównane}}}$

i są funkcjami Theta modułu $Theta$$u$ \ $}$ u Powiązana macierz $;$$jest$ zatem funkcją dla wszystkich ${\ displaystyle u}$ , ${\ displaystyle v}$

${\ Displaystyle T (u) T (v) = T (v) T (u).}$

Funkcja macierzowa ${\ Displaystyle Q (u)}$

Inną kluczową częścią rozwiązania jest istnienie nieosobliwej funkcji o wartościach macierzowych $displaystyle Q(u),Q(u')}$$takiej$ , że dla wszystkich złożonych Q $,$ dojeżdżają do pracy między sobą i macierzami transferu i spełniają

${\ Displaystyle \ zeta (u) T ( u)Q(u)=\phi (u-\eta )Q(u+2\eta )+\phi (u+\eta )Q(u-2\eta )}$

 

 

 

 

()

Gdzie

${\ Displaystyle {\ rozpocząć {wyrównane} \ zeta (u) & = [c ^ {-1} H (2 \ eta) \ Theta (u- \ eta) \ Theta (u + \ eta)] ^ {N} \ \\phi (u)&=[\Theta (0)H(u)\Theta (u)]^{N}.\end{wyrównane}}}$

Istnienie i relacje komutacji takiej funkcji są demonstrowane przez rozważenie propagacji par przez wierzchołek i relacje okresowości funkcji theta, w podobny sposób jak w modelu sześciu wierzchołków.

Jawne rozwiązanie

Komutacja macierzy w ( 1 ) pozwala na ich diagonalizację , a zatem można znaleźć wartości własne . Funkcja podziału jest obliczana na podstawie maksymalnej wartości własnej, co daje energię swobodną na miejsce

${\ Displaystyle {\ rozpocząć {wyrównane} f = \ epsilon _ {5} -2kT \ suma _ {n = 1} ^ {\ infty}} {\ Frac {\ sinh ^ {2} ((\ tau - \lambda )n)(\cosh(n\lambda )-\cosh(n\alpha ))}{n\sinh(2n\tau )\cosh(n\lambda )}}\end{wyrównane}}}$

Do

${\ Displaystyle {\ rozpocząć {wyrównane} \ tau & = {\ Frac {\ pi K'} {2K}} \\\ lambda & ={\frac {\pi \eta }{iK}}\\\alpha &={\frac {\pi u}{iK}}\end{wyrównane}}}$

gdzie $i$$k$ kompletnymi całekami eliptycznymi modułów k $}$$displaystyle$ ' Model ośmiu wierzchołków został również rozwiązany w kwazikryształach .

Równoważność z modelem Isinga

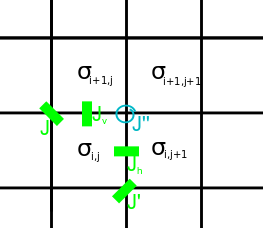
Istnieje naturalna zgodność między modelem ośmiu wierzchołków a modelem Isinga z 2-spinowymi i 4-spinowymi interakcjami najbliższego sąsiada. Stany tego modelu to spiny na ścianach kwadratowej sieci ${\ displaystyle \ sigma = \ pm 1} .$ Analogiem „krawędzi” w modelu ośmiu wierzchołków są iloczyny spinów na sąsiednich ścianach:

${\ Displaystyle {\ rozpocząć {wyrównane} \ alfa _ {ij} & = \ sigma _ {ij} \ sigma _ {i, j + 1} \\\ mu _ {ij} & = \ sigma _ {ij} \ sigma _{i+1,j}.\end{wyrównane}}}$

Najbardziej ogólną postacią energii dla tego modelu jest

${\ Displaystyle {\ rozpocząć {wyrównane} \ epsilon & = - \ suma _ {ij} (J_ {h} \ mu _ {ij} + J_ {v} \ alfa _ {ij} + J \ alfa _ {ij }\mu _{ij}+J'\alpha _{i+1,j}\mu _{ij}+J''\alpha _{ij}\alpha _{i+1,j})\end{ wyrównany}}}$

gdzie ${\ Displaystyle J_ {h}}$ , ${\ Displaystyle J_ {v}}$ , ${\ Displaystyle J}$ , ${\ Displaystyle J'}$ opisują poziome, pionowe i dwie ukośne interakcje 2-spinowe i opisuje 4-spinową interakcję między czterema ścianami w wierzchołku; ${\ Displaystyle J''}$ suma obejmuje całą kratę.

Oznaczamy odpowiednio poziome i pionowe spiny (strzałki na krawędziach) w modelu z ośmioma wierzchołkami $i$ definiujemy $w$ górę iw prawo jako kierunki dodatnie Ograniczenie stanów wierzchołków polega na tym, że iloczyn czterech krawędzi w wierzchołku wynosi 1; automatycznie odnosi się to do „krawędzi” Isinga. Każda konfiguracja odpowiada zatem unikalnej konfiguracji, podczas gdy każda konfiguracja $\$ μ $α$$\ displaystyle \ mu}$$alpha$ \ $}$$konfiguracji$ opcje .

Zrównując ogólne formy wag Boltzmanna dla każdego wierzchołka , następujące relacje między $Displaystyle \ epsilon _ {j}}$${\$ i ${\ Displaystyle J_ {h}}$ J $\ Displaystyle J_ {v}}$ , ${\ displaystyle J}$ , ${\ displaystyle J'}$ , ${\ displaystyle J''}$ zdefiniuj zgodność między modelami kratowymi:

${\ Displaystyle {\ rozpocząć {wyrównane} \ epsilon _ {1} & = -J_ {h} -J_ {v} -JJ '-J '', \ quad \ epsilon _ {2} = J_ {h} + J_ {v}-JJ'-J''\\\epsilon _{3}&=-J_{h}+J_{v}+J+J'-J'',\quad \epsilon _{4}=J_ {h}-J_{v}+J+J'-J''\\\epsilon _{5}&=\epsilon _{6}=JJ'+J''\\\epsilon _{7}&= \epsilon _{8}=-J+J'+J''.\end{wyrównane}}}$

Wynika z tego, że w przypadku pola zerowego modelu z ośmioma wierzchołkami poziome i pionowe interakcje w odpowiednim modelu Isinga znikają.

$dają$ równoważność między funkcjami podziału modelu ośmiu wierzchołków W konsekwencji rozwiązanie w jednym z modeli prowadziłoby bezpośrednio do rozwiązania w drugim.

Zobacz też

• Model sześciu wierzchołków
• Metoda macierzy przenoszenia
• Model Isinga

Notatki

•    Baxter, Rodney J. (1982), Dokładnie rozwiązane modele mechaniki statystycznej (PDF) , Londyn: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7 , MR 0690578 , zarchiwizowane z oryginału (PDF) w dniu 2021-04-14 , pobrane 2012-08-12