Odległość Frécheta

W matematyce odległość Frécheta jest miarą podobieństwa między krzywymi , która uwzględnia położenie i uporządkowanie punktów wzdłuż krzywych. Jej nazwa pochodzi od imienia Maurice'a Frécheta .

Intuicyjna definicja

Wyobraź sobie osobę przemierzającą skończoną zakrzywioną ścieżkę podczas wyprowadzania psa na smyczy, przy czym pies przechodzi przez oddzielną skończoną zakrzywioną ścieżkę. Każdy może zmieniać prędkość, aby utrzymać luz na smyczy, ale żaden nie może się cofnąć. Odległość Frécheta między dwoma krzywymi to długość najkrótszej smyczy, która jest wystarczająca dla obu do pokonania oddzielnych ścieżek od początku do końca. Zauważ, że definicja jest symetryczna w odniesieniu do dwóch krzywych - odległość Frécheta byłaby taka sama, gdyby pies spacerował ze swoim właścicielem.

Definicja formalna

Niech będzie przestrzenią $metryczną$ . Krzywa $\$ jest $ciągłą$ mapą od przedziału jednostkowego do , tj $A$ [ ] $Displaystyle$ 0,1 . Reparametryzacja z $Displaystyle [0,1]}$ $\$ ${\ Displaystyle \ alpha:$ ciągłą, nie malejącą surjekcją : .

Niech $i będą dwiema$ $displaystyle$ krzywymi w $S}$ \ . Następnie $\ Displaystyle [0,1]}$ Frécheta między i jest $}$ jako po wszystkich reparametryzacjach i $Displaystyle \ beta$ $\$ $[$ { maksimum na wszystkich ${\ Displaystyle t \ w [0,1]}$ odległości w ${\ Displaystyle S}$ między ${\ Displaystyle ZA (\ alfa (t))}$ i ${\ Displaystyle B (\ beta (t))}$ . W notacji matematycznej odległość Frécheta wynosi ${\ Displaystyle F (A, B)}$

${\ Displaystyle F (A, B) = \ inf _{\alpha ,\beta }\,\,\max _{t\in [0,1]}\,\,{\Bigg \{}d{\Big (}A(\alpha (t)), \,B(\beta (t)){\Duży )}{\Bigg \}}}$

gdzie jest funkcją odległości $displaystyle$ $S}$ .

Nieformalnie możemy myśleć o parametrze $.$ o „czasie” Wtedy $($ pozycja psa i jest pozycją t $\$ właściciela psa w czasie $.$ lub odwrotnie) Długość smyczy między nimi w czasie ${\ Displaystyle B (\beta (t))}$ $t$ między ${\ Displaystyle A (\ alfa (t))}$ i . Przejęcie infimum po wszystkich możliwych reparametryzacjach $jest$ spaceru po podanych ścieżkach, gdzie maksymalna długość Ograniczenie, że i nie $maleją$ $,$ oznacza, że ani pies, ani jego właściciel nie mogą się

Metryka Frécheta uwzględnia przepływ dwóch krzywych, ponieważ pary punktów, których odległość przyczynia się do odległości Frécheta, przechodzą w sposób ciągły wzdłuż odpowiednich krzywych. To sprawia, że odległość Frécheta jest lepszą miarą podobieństwa krzywych niż alternatywy, takie jak odległość Hausdorffa , dla dowolnych zbiorów punktów. Możliwe jest, aby dwie krzywe miały małą odległość Hausdorffa, ale dużą odległość Frécheta.

Odległość Frécheta i jej warianty znajdują zastosowanie w kilku problemach, od morfingu i rozpoznawania pisma ręcznego po wyrównanie struktury białek . Alt i Godau jako pierwsi opisali algorytm czasu wielomianowego do obliczania odległości Frécheta między dwiema krzywymi wielokątnymi w przestrzeni euklidesowej , w oparciu o zasadę wyszukiwania parametrycznego . Czas $_$ dla z _ _ _

Diagram wolnej przestrzeni

Diagram wolnej przestrzeni krzywej czerwonej i niebieskiej. W przeciwieństwie do definicji w tekście, która używa przedziału parametru [0,1] dla obu krzywych, w tym przykładzie krzywe są sparametryzowane na podstawie długości łuku.

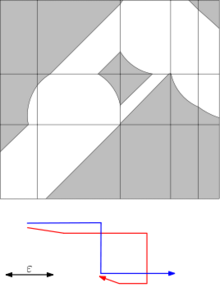
Ważnym narzędziem do obliczania odległości Frécheta dwóch krzywych jest diagram wolnej przestrzeni, który został wprowadzony przez Alta i Godau. Diagram wolnej przestrzeni między dwiema krzywymi dla danego progu odległości ε jest dwuwymiarowym obszarem w przestrzeni parametrów, który składa się ze wszystkich par punktów na dwóch krzywych w odległości co najwyżej ε:

${\ Displaystyle D _ {\ varepsilon} (A, B) :=\{\,(\alpha ,\beta )\in [0,1]^{2}\mid d(A(\alpha ),B(\beta ))\leq \varepsilon \,\}}$

Odległość Frécheta $D$ $B)}$ ) $} ($ zawiera ścieżkę od lewego dolnego rogu do prawego górnego rogu, która jest monotonna zarówno w kierunku poziomym, jak i pionowym.

Jako odległość między rozkładami prawdopodobieństwa (wynik FID)

Oprócz pomiaru odległości między krzywymi, odległość Frécheta może być również wykorzystana do pomiaru różnicy między rozkładami prawdopodobieństwa .

$\ mu _ {$ $X$ ze średnimi i macierzami kowariancji i Σ $}$ i ${\ displaystyle \ Sigma _ {Y}}$ odległość Frécheta między tymi rozkładami wynosi

${\ Displaystyle d ^ {2} = | \ mu _ {X} - \ mu _ {Y} | ^ {2} +\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})}$ .

Ta odległość jest podstawą odległości początkowej Frécheta (FID), która jest używana do porównywania obrazów wytwarzanych przez generatywną sieć przeciwstawną z rzeczywistymi obrazami używanymi do treningu.

Warianty

Słaba odległość Frécheta jest wariantem klasycznej odległości Frécheta bez wymogu, aby punkty końcowe poruszały się monotonicznie wzdłuż odpowiednich krzywych - pies i jego właściciel mogą cofać się, aby smycz między nimi była krótka. Alt i Godau opisują prostszy algorytm do obliczania słabej odległości Frécheta między krzywymi wielokątnymi, oparty na obliczaniu ścieżek minimax w powiązanym wykresie siatki .

Dyskretna odległość Frécheta , zwana także odległością sprzężenia , jest przybliżeniem metryki Frécheta dla krzywych wielokątnych, zdefiniowanej przez Eitera i Mannilę. Dyskretna odległość Frécheta uwzględnia tylko pozycje smyczy, w których jej punkty końcowe znajdują się w wierzchołkach dwóch wielokątnych krzywych, a nigdy we wnętrzu krawędzi. Ta specjalna struktura umożliwia obliczenie dyskretnej odległości Frécheta w czasie wielomianowym za pomocą łatwego algorytmu programowania dynamicznego.

Kiedy dwie krzywe są osadzone w przestrzeni metrycznej innej niż przestrzeń euklidesowa, takiej jak teren wielościenny lub przestrzeń euklidesowa z przeszkodami, odległość między dwoma punktami na krzywych jest najbardziej naturalnie definiowana jako długość najkrótszej ścieżki między nimi. Smycz musi być geodezyjna łącząca swoje punkty końcowe. Wynikowa metryka między krzywymi nazywana jest geodezyjną odległością Frécheta . Cook i Wenk opisują algorytm czasu wielomianowego do obliczania geodezyjnej odległości Frécheta między dwiema krzywymi wielokątnymi w prostym wielokącie .

Jeśli dodatkowo wymagamy, aby smycz poruszała się w sposób ciągły w otaczającej przestrzeni metrycznej, to otrzymujemy pojęcie homotopijnej odległości Frécheta między dwiema krzywymi. Smycz nie może zmieniać się w sposób nieciągły z jednej pozycji do drugiej - w szczególności smycz nie może przeskakiwać przez przeszkody i może zamiatać górę po terenie tylko wtedy, gdy jest wystarczająco długa. Ruch smyczy opisuje homotopię między dwiema krzywymi. Chambers i in. opisz algorytm czasu wielomianowego do obliczania homotopijnej odległości Frécheta między krzywymi wielokątnymi na płaszczyźnie euklidesowej z przeszkodami.

Przykłady

Odległość Frécheta między dwoma koncentrycznymi okręgami o promieniu odpowiednio ${\ displaystyle r_ {1}}$ i ${\ displaystyle r_ {2}}$ wynosi ${\ Displaystyle | r_ {1} -r_ {2} |.}$ Najdłuższa smycz jest wymagana, gdy właściciel stoi nieruchomo, a pies przechodzi na drugą stronę koła ( ${\ displaystyle r_ {1} + r_ {2}}$ ) i najkrótsza smycz, gdy zarówno właściciel, jak i pies chodzą ze stałą prędkością kątową po okręgu ( ${\ Displaystyle | r_ {1} -r_ {2}|}$ ) .

Aplikacje

Odległość Frécheta została wykorzystana do badania hierarchii wizualnej , zasady projektowania graficznego.

Zobacz też

Dalsza lektura

de Berg, Mark, „Analiza trajektorii poruszających się obiektów”, geometria obliczeniowa, dwa wybrane tematy (PDF) , s. 11–75 .
Aronow, Borys ; Har-Peled, Sariel; Knauer, chrześcijanin; Wang, Yusu ; Wenk, Carola (2006), „Odległość Frécheta dla krzywych, powtórka”, Proc. 14. Europejskie Sympozjum Algorytmów (PDF) , Notatki z wykładów z informatyki, tom. 4168, Springer-Verlag, s. 52–63, arXiv : 1504.07685 , doi : 10.1007/11841036_8 , zarchiwizowane z oryginału (PDF) w dniu 12.06.2010 .
Alt, Helmut ; Buchin, Maike (2010), „Czy możemy obliczyć podobieństwo między powierzchniami?”, Discrete and Computational Geometry , 43 : 78–99, arXiv : cs.CG/0703011 , doi : 10.1007/s00454-009-9152-8 .