Płaszczyzna polaryzacji

  Ryc. 1 : Wektory pola ( E , D , B , H ) i kierunki propagacji (promienie i fale normalne) dla liniowo spolaryzowanych płaskich fal elektromagnetycznych w niemagnetycznym krysztale dwójłomnym. Płaszczyzna drgań, zawierająca zarówno wektory elektryczne ( E i D ), jak i oba wektory propagacji, jest czasami nazywana przez współczesnych autorów „płaszczyzną polaryzacji”. „Płaszczyzna polaryzacji” Fresnela, tradycyjnie stosowana w optyce, to płaszczyzna zawierająca wektory magnetyczne ( B i H ) i normalną falową . Oryginalna „płaszczyzna polaryzacji” Malusa była płaszczyzną zawierającą wektory magnetyczne i promień . (W ośrodku izotropowym θ = 0 i płaszczyzna Malusa łączy się z płaszczyzną Fresnela.)

W przypadku światła i innego promieniowania elektromagnetycznego płaszczyzną polaryzacji jest płaszczyzna rozpięta przez kierunek propagacji oraz wektor elektryczny lub wektor magnetyczny , w zależności od konwencji. Można go zdefiniować dla spolaryzowanego , pozostaje nieruchomy w przestrzeni dla światła spolaryzowanego liniowo i podlega obrotowi osiowemu dla światła spolaryzowanego kołowo .

Niestety, te dwie konwencje są ze sobą sprzeczne. Jak pierwotnie zdefiniował Étienne-Louis Malus w 1811 r., płaszczyzna polaryzacji pokrywała się (choć nie było to wówczas znane) z płaszczyzną zawierającą kierunek propagacji i wektor magnetyczny . We współczesnej literaturze termin płaszczyzna polaryzacji , jeśli w ogóle jest używany, prawdopodobnie będzie oznaczać płaszczyznę zawierającą kierunek propagacji i wektor elektryczny , ponieważ pole elektryczne ma większą skłonność do oddziaływania z materią.

W przypadku fal w krysztale dwójłomnym (podwójnie załamującym), zgodnie ze starą definicją, należy również określić, czy kierunek propagacji oznacza kierunek promienia ( wektor Poyntinga ), czy kierunek normalny fali , ponieważ kierunki te na ogół są różne i oba są prostopadłe do wektora magnetycznego (ryc. 1). Malus, jako zwolennik korpuskularnej teorii światła , mógł jedynie wybierać kierunek promienia. Ale Augustin-Jean Fresnel w swojej udanej próbie wyjaśnienia podwójnego załamania w ramach teorii fal (1822 i później) uznali, że bardziej przydatny jest wybór kierunku normalnego fali, w wyniku czego przypuszczalne drgania ośrodka są wówczas konsekwentnie prostopadłe do płaszczyzny polaryzacji. W izotropowym , takim jak powietrze, kierunek normalny promienia i fali jest taki sam, a modyfikacja Fresnela nie ma żadnego znaczenia.

Fresnel przyznał także, że gdyby nie czuł się ograniczony przez przyjętą terminologię, bardziej naturalne byłoby zdefiniowanie płaszczyzny polaryzacji jako płaszczyzny zawierającej drgania i kierunek propagacji. Płaszczyzna ta, znana jako płaszczyzna wibracji , jest prostopadła do „płaszczyzny polaryzacji” Fresnela, ale identyczna z płaszczyzną, którą współcześni pisarze zwykle nazywają tą nazwą!

Argumentowano, że w tekstach oryginalnych należy unikać terminu płaszczyzna polaryzacji ze względu na jego historyczną dwuznaczność. Można łatwo określić orientację konkretnego wektora pola; a nawet termin płaszczyzna wibracji niesie ze sobą mniejsze ryzyko nieporozumień niż płaszczyzna polaryzacji .

Fizyka terminu

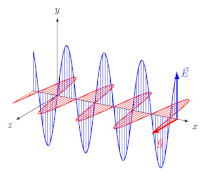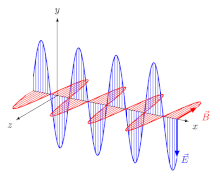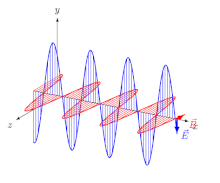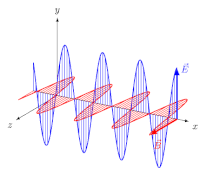
  Ryc. 2 : Liniowo spolaryzowana (spolaryzowana płasko) sinusoidalna fala elektromagnetyczna w ośrodku izotropowym , rozchodząca się w kierunku x (kierunek promienia i kierunek normalny fali), z wektorami pola elektrycznego E i D w kierunku y oraz wektory pola magnetycznego B i H w kierunku z . (Sytuacja w nieizotropowym jest bardziej skomplikowana; por. ryc. 1.)

W przypadku fal elektromagnetycznych (EM) w ośrodku izotropowym (to znaczy ośrodku, którego właściwości są niezależne od kierunku), wektory pola elektrycznego ( E i D ) są w jednym kierunku, a wektory pola magnetycznego ( B i H ) są w jednym kierunku inny kierunek, prostopadły do ​​pierwszego, a kierunek propagacji jest prostopadły zarówno do wektora elektrycznego, jak i magnetycznego. W tym przypadku kierunkiem propagacji jest zarówno promienia , jak i normalny fali (kierunek prostopadły do ​​czoła fali ). Dla spolaryzowanej liniowo (zwanej także falą spolaryzowaną płasko) orientacje wektorów pola są stałe (rys. 2).

Ponieważ niezliczona ilość materiałów to dielektryki lub przewodniki , a stosunkowo niewiele to ferromagnetyki , odbicie lub załamanie fal elektromagnetycznych (w tym światła ) częściej wynika z różnic we właściwościach elektrycznych mediów niż z różnic w ich właściwościach magnetycznych. Ta okoliczność zwykle zwraca uwagę na elektrykę wektory, tak że mamy tendencję do myślenia o kierunku polaryzacji jako o kierunku wektorów elektrycznych, a o „płaszczyźnie polaryzacji” jako o płaszczyźnie zawierającej wektory elektryczne i kierunek propagacji.

  Ryc. 3 : Antena mikrofalowa z polaryzacją pionową, paraboliczną . W tym przypadku podana polaryzacja odnosi się do ustawienia pola elektrycznego ( E ), a więc do ustawienia blisko rozmieszczonych metalowych żeberek w reflektorze.

Rzeczywiście, taką konwencję zastosowano w internetowej Encyklopedii Britannica oraz w wykładzie Feynmana na temat polaryzacji. W tym drugim przypadku konwencję należy wywnioskować z kontekstu: Feynman cały czas podkreśla kierunek wektora elektrycznego ( E ) i pozostawia czytelnikowi domniemanie, że „płaszczyzna polaryzacji” zawiera ten wektor — i ta interpretacja rzeczywiście pasuje do przykładów, które podał daje. Ten sam wektor służy do opisu polaryzacji sygnałów radiowych i anten (ryc. 3).

Jeśli ośrodek jest magnetycznie izotropowy, ale elektrycznie nieizotopowy (jak kryształ podwójnie załamujący światło), wektory magnetyczne B i H są nadal równoległe, a wektory elektryczne E i D są nadal prostopadłe do obu, a kierunek promienia jest nadal prostopadły do E i wektorów magnetycznych, a kierunek normalny fali jest nadal prostopadły do ​​D i wektorów magnetycznych; ale ogólnie istnieje mały kąt między wektorami elektrycznymi E i D   , stąd ten sam kąt między kierunkiem promienia a kierunkiem normalnej fali (ryc. 1). Stąd D , E , kierunek normalny fali i kierunek promienia znajdują się w tej samej płaszczyźnie, a tym bardziej naturalne jest zdefiniowanie tej płaszczyzny jako „płaszczyzny polaryzacji”.

Ta „naturalna” definicja opiera się jednak na teorii fal elektromagnetycznych opracowanej przez Jamesa Clerka Maxwella w latach sześćdziesiątych XIX wieku – podczas gdy słowo polaryzacja powstało około 50 lat wcześniej, a związana z nim tajemnica sięga jeszcze dalej.

Historia terminu

Trzej kandydaci

Czy to przez przypadek, czy z założenia, płaszczyzna polaryzacji zawsze była definiowana jako płaszczyzna zawierająca wektor pola i kierunek propagacji. Na rys. 1 przedstawiono trzy takie płaszczyzny, którym dla ułatwienia można przypisać numery:

(1) płaszczyzna zawierająca oba wektory elektryczne i oba kierunki propagacji (tj. płaszczyznę prostopadłą do wektorów magnetycznych);
(2a) płaszczyzna zawierająca wektory magnetyczne i normalną falową (tj. płaszczyzna normalna do D );
(2b) płaszczyzna zawierająca wektory magnetyczne i promień (tj. płaszczyzna normalna do E ).

W ośrodku izotropowym E i D mają ten sam kierunek, tak że kierunki normalne do fali i promienia łączą się, a płaszczyzny (2a) i (2b) stają się jedną:

(2) płaszczyzna zawierająca oba wektory magnetyczne i oba kierunki propagacji (tj. płaszczyznę prostopadłą do wektorów elektrycznych).

Wybór Malusa

  Ryc. 4 : Wydrukowana etykieta widziana przez podwójnie załamujący kryształ kalcytu i nowoczesny filtr polaryzacyjny (obrócony, aby pokazać różne polaryzacje dwóch obrazów).

Polaryzację odkrył – choć nie nazwał jej ani nie rozumiał – Christiaan Huygens , badając podwójne załamanie „islandzkiego kryształu” (przezroczystego kalcytu , obecnie zwanego drzewcem islandzkim ). Istota jego odkrycia, opublikowana w Traktacie o świetle (1690), była następująca. Kiedy promień (czyli wąska wiązka światła) przechodzi przez dwa podobnie zorientowane kryształy kalcytu z normalnym padaniem, zwykły promień wychodzący z pierwszego kryształu ulega jedynie zwykłemu załamaniu w drugim, podczas gdy niezwykły promień wychodzący z pierwszego ulega jedynie niezwykłe załamanie w drugim. Kiedy jednak drugi kryształ obróci się o 90° wokół padających promieni, role ulegają zamianie, tak że zwykły promień wychodzący z pierwszego kryształu ulega jedynie niezwykłemu załamaniu w drugim i odwrotnie. W pośrednich pozycjach drugiego kryształu każdy promień wychodzący z pierwszego jest podwójnie załamywany przez drugi, dając w sumie cztery promienie; a gdy kryształ jest obracany od orientacji początkowej do orientacji prostopadłej, jasność promieni zmienia się, dając płynne przejście pomiędzy skrajnymi przypadkami, w których są tylko dwa promienie końcowe.

Huygens zdefiniował główny przekrój kryształu kalcytu jako płaszczyznę prostopadłą do naturalnej powierzchni i równoległą do osi kąta rozwartego. Oś ta była równoległa do osi sferoidalnych fal wtórnych , za pomocą których (poprawnie) wyjaśnił kierunki niezwykłego załamania.

Étienne-Louis Malus (1775–1812).

Termin polaryzacja został ukuty przez Étienne-Louis Malus w 1811 r. W 1808 r., w trakcie potwierdzania geometrycznego opisu podwójnego załamania przez Huygensa (kwestionując jego fizyczne wyjaśnienie), Malus odkrył, że kiedy promień światła odbija się od nie -metaliczna powierzchnia pod odpowiednim kątem zachowuje się jak jeden z dwóch promieni wychodzących z kryształu kalcytu. Ponieważ to zachowanie było wcześniej znane tylko w związku z podwójnym załamaniem, Malus opisał je w tym kontekście. W szczególności zdefiniował płaszczyznę polaryzacji spolaryzowanego promienia jako płaszczyzny zawierającej promień, w której musi leżeć główna część kryształu kalcytu, aby powodować jedynie zwykłe załamanie. Definicja ta była tym bardziej rozsądna, że ​​oznaczała, że ​​gdy promień był spolaryzowany przez odbicie (od ośrodka izotopowego), płaszczyzną polaryzacji była płaszczyzna padania i odbicia, to znaczy płaszczyzna zawierająca promień padający, normalna do powierzchnia odbijająca i spolaryzowany promień odbity. Ale jak już wiemy, płaszczyzna ta zawiera magnetyczne promienia spolaryzowanego, a nie wektory elektryczne.

Płaszczyzną promienia i wektorów magnetycznych jest ta o numerze (2b) powyżej. Sugestię, że płaszczyzna polaryzacji zawiera magnetyczne , nadal można znaleźć w definicji podanej w internetowym słowniku Merriam-Webster. Nawet Julius Adams Stratton , stwierdzając, że „zwyczajowo definiuje się polaryzację w kategoriach E ”, natychmiast dodaje: „Jednak w optyce orientacja wektorów jest tradycyjnie określana przez „płaszczyznę polaryzacji”, za pomocą której oznaczało płaszczyznę normalną do E zawierającą zarówno H i oś propagacji.” Ta definicja jest identyczna z definicją Malusa.

Wybór Fresnela

Augustin-Jean Fresnel (1788–1827).

W 1821 roku Augustin-Jean Fresnel ogłosił swoją hipotezę, że fale świetlne są wyłącznie poprzeczne , a zatem zawsze spolaryzowane w tym sensie, że mają określoną orientację poprzeczną, oraz że to, co nazywamy światłem niespolaryzowanym , to w rzeczywistości światło, którego orientacja zmienia się szybko i losowo. Zakładając, że fale świetlne są analogiczne do fal ścinających w elastycznych ciałach stałych i że wyższy współczynnik załamania światła odpowiada większej gęstości świetlistego eteru odkrył, że może wyjaśnić częściowe odbicie (w tym polaryzację przez odbicie) na styku dwóch przezroczystych ośrodków izotropowych, pod warunkiem, że wibracje eteru są prostopadłe do płaszczyzny polaryzacji. Zatem polaryzacja, zgodnie z otrzymaną definicją, znajdowała się „w” pewnej płaszczyźnie, jeśli drgania były prostopadłe do tej płaszczyzny!

Sam Fresnel uznał tę implikację za niewygodną; później w tym samym roku napisał:

Przyjmując tę ​​hipotezę, bardziej naturalne byłoby nazwanie płaszczyzny polaryzacji tą, w której przypuszcza się, że zachodzą oscylacje, chciałem jednak uniknąć dokonywania jakichkolwiek zmian w otrzymanych nazwach.

Wkrótce jednak poczuł się zobowiązany do wprowadzenia mniej radykalnych zmian. W jego udanym modelu podwójnego załamania przemieszczenie ośrodka było ograniczone do stycznego do czoła fali, podczas gdy siła mogła odchylać się od przemieszczenia i od czoła fali. Zatem jeśli drgania były prostopadłe do płaszczyzny polaryzacji, wówczas płaszczyzna polaryzacji zawierała normalną falową, ale niekoniecznie promień. W swoim „Drugim wspomnieniu” na temat podwójnego załamania światła Fresnel formalnie przyjął tę nową definicję, potwierdzając, że jest ona zgodna ze starą definicją w ośrodku izotropowym, takim jak powietrze, ale nie w krysztale dwójłomnym.

Drgania normalne do płaszczyzny polaryzacji Malusa mają charakter elektryczny, a drgania elektryczne styczne do czoła fali wynoszą D (ryc. 1). Zatem biorąc pod uwagę powyższą numerację, Fresnel zmienił „płaszczyznę polaryzacji” z (2b) na (2a) . Definicja Fresnela pozostaje zgodna z definicją Merriama-Webstera, która nie określa kierunku propagacji. I pozostaje to zgodne z definicją Strattona, ponieważ jest ona podana w kontekście ośrodka izotropowego, w którym płaszczyzny (2a) i (2b) łączą się w (2) .

Tym, co Fresnel nazwał „bardziej naturalnym” wyborem, była płaszczyzna zawierająca D i kierunek propagacji. Na ryc. 1 jedyną płaszczyzną spełniającą tę specyfikację jest ta oznaczona jako „Płaszczyzna wibracji” i później oznaczona numerem (1) — czyli ta, którą współcześnie autorzy mają tendencję do identyfikowania się z „płaszczyzną polaryzacji”. Moglibyśmy zatem żałować, że Fresnel nie okazywał swoim poprzednikom mniejszego szacunku. Scenariusz ten jest jednak mniej realistyczny, niż mogłoby się wydawać, gdyż nawet po powszechnym przyjęciu teorii fali poprzecznej Fresnela kierunek drgań był przedmiotem ciągłej debaty.

„Płaszczyzna wibracji”

Zasada, że ​​współczynnik załamania światła zależy od gęstości eteru, była istotna dla hipotezy oporu eteru Fresnela . Nie można go jednak rozszerzyć na kryształy dwójłomne, w których co najmniej jeden współczynnik załamania światła zmienia się w zależności od kierunku, ponieważ gęstość nie jest kierunkowa. Dlatego jego wyjaśnienie załamania wymagało kierunkowej zmiany sztywności eteru w ośrodku dwójłomnym oraz zmiany gęstości pomiędzy ośrodkami.

James MacCullagh i Franz Ernst Neumann uniknęli tej komplikacji, zakładając, że wyższy współczynnik załamania światła odpowiada zawsze tej samej gęstości, ale większej podatności sprężystej (mniejsza sztywność). Aby uzyskać wyniki zgodne z obserwacjami częściowego odbicia, należało założyć, w przeciwieństwie do Fresnela, że ​​drgania mieszczą się w płaszczyźnie polaryzacji.

George Gabriel Stokes (1819–1903).

Pytanie wymagało eksperymentalnego określenia kierunku drgań, a na wyzwanie odpowiedział George Gabriel Stokes . Zdefiniował płaszczyznę drgań jako „płaszczyznę przechodzącą przez promień i kierunek drgań” (zgodnie z rys. 1). Załóżmy teraz, że mamy do czynienia z drobną siatką dyfrakcyjną świeci się z normalną częstotliwością. Przy dużych kątach dyfrakcji siatka będzie wyglądać nieco krawędziowo, tak że kierunki drgań będą skupione w kierunku równoległym do płaszczyzny siatki. Jeśli płaszczyzny polaryzacji pokrywają się z płaszczyznami wibracji (jak powiedzieli MacCullagh i Neumann), będą one stłoczone w tym samym kierunku; i jeśli płaszczyzny polaryzacji są normalne do płaszczyzn drgań (jak powiedział Fresnel), płaszczyzny polaryzacji będą stłoczone w kierunku normalnym. Aby znaleźć kierunek stłoczenia, można zmieniać polaryzację padającego światła w równych krokach i w zwykły sposób wyznaczać płaszczyzny polaryzacji światła ugiętego. Stokes przeprowadził taki eksperyment w 1849 roku i okazał się korzystny dla Fresnela.

W 1852 roku Stokes zaobserwował znacznie prostszy eksperyment, który prowadzi do tego samego wniosku. Metodą Malusa stwierdzono, że światło słoneczne rozproszone z kawałka błękitnego nieba pod kątem 90° od Słońca jest spolaryzowane w płaszczyźnie zawierającej linię wzroku i słońce. Ale z geometrii jasno wynika, że ​​wibracje tego światła mogą być tylko prostopadłe do tej płaszczyzny.

Jednak w pewnym sensie MacCullagh i Neumann mieli rację. Jeśli spróbujemy zastosować analogię pomiędzy falami ścinającymi w nieizotropowym elastycznym ciele stałym i falami EM w magnetycznie izotropowym, ale elektrycznie nieizotropowym krysztale, gęstość musi odpowiadać przenikalności magnetycznej (oba są bezkierunkowe), a zgodność musi odpowiadają przenikalności elektrycznej (obie są kierunkowe). W rezultacie prędkość ciała stałego odpowiada polu H , tak że drgania mechaniczne fali ścinającej są skierowane w kierunku pola magnetycznego drgania fali EM. Ale eksperymenty Stokesa musiały wykryć elektryczne , ponieważ mają one większą skłonność do interakcji z materią. Krótko mówiąc, drgania MacCullagha-Neumanna miały mechaniczny odpowiednik, ale drgania Fresnela były tymi, które z większym prawdopodobieństwem można było wykryć w eksperymentach.

Nowoczesna praktyka

Elektromagnetyczna teoria światła dodatkowo kładła nacisk na wibracje elektryczne ze względu na ich interakcje z materią, podczas gdy stara „płaszczyzna polaryzacji” zawierała wektory magnetyczne . Stąd teoria elektromagnetyczna wzmocniłaby konwencję, że drgania są normalne do płaszczyzny polaryzacji – oczywiście pod warunkiem, że zna się historyczną definicję płaszczyzny polaryzacji. Ale jeśli ktoś kierował się wyłącznie względami fizycznymi , to tak jak Feynman i Britannica ilustrując, należałoby zwrócić uwagę na wektory elektryczne i założyć, że „płaszczyzna” polaryzacji (jeśli potrzeba takiego pojęcia) zawiera te wektory.

Nie jest jednak jasne, czy „płaszczyzna polaryzacji” jest w ogóle potrzebna: wiedząc, jakie wektory pola wchodzą w grę, można określić polaryzację poprzez określenie orientacji konkretnego wektora lub, jak sugerują Born i Wolf , poprzez określenie „płaszczyzna drgań” tego wektora. Hecht preferuje również termin płaszczyzna wibracji (lub, częściej, płaszczyzna wibracji ), którą definiuje jako płaszczyznę E i normalną falową, zgodnie z rys. 1 powyżej.

Pozostałe zastosowania

W ośrodku optycznie chiralnym - to znaczy takim, w którym kierunek polaryzacji stopniowo zmienia się w miarę rozchodzenia się fali - wybór definicji „płaszczyzny polaryzacji” nie wpływa na istnienie ani kierunek („ręczność”) obrotu. Jest to jeden z kontekstów, w którym dwuznaczność terminu płaszczyzna polaryzacji nie powoduje dalszego zamieszania.

Istnieje również kontekst, w którym pierwotna definicja może nadal nasuwać się sama. W niemagnetycznym, niechiralnym krysztale klasy dwuosiowej (w którym nie zachodzi zwykłe załamanie, ale oba załamania naruszają prawo Snella ) istnieją trzy wzajemnie prostopadłe płaszczyzny, dla których prędkość światła jest w obrębie tej płaszczyzny izotropowa pod warunkiem, że wektory elektryczne są normalne do płaszczyzny. Sytuacja ta w naturalny sposób zwraca uwagę na płaszczyznę normalną do wibracji przewidywaną przez Fresnela i płaszczyzna ta jest w istocie płaszczyzną polaryzacji określoną przez Fresnela lub Malusa.

Jednakże w większości kontekstów koncepcja „płaszczyzny polaryzacji” odrębnej od płaszczyzny zawierającej „wibracje” elektryczne stała się prawdopodobnie zbędna i z pewnością stała się źródłem zamieszania. Według słów Born & Wolf: „lepiej… lepiej nie używać tego terminu”.

Zobacz też

Notatki

Bibliografia

Źródło: „ https://en.wikipedia.org/w/index.php?title=Plane_of_polarization&oldid=1143058625 ”