Powierzchnia katalońska

Ten artykuł dotyczy powierzchni rządzonych. Aby zapoznać się z minimalną powierzchnią, zobacz minimalną powierzchnię katalońskiego .

Katalońska powierzchnia.

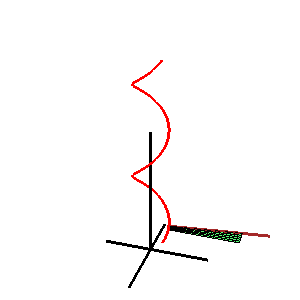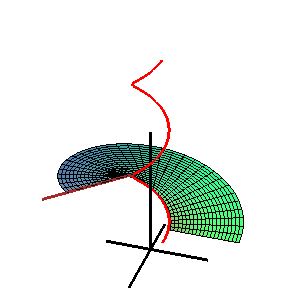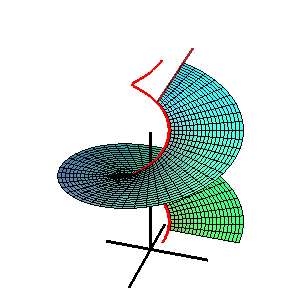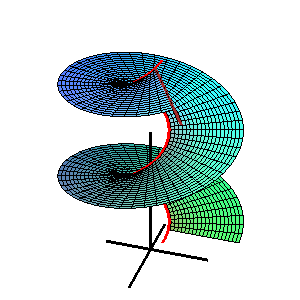
W geometrii powierzchnia katalońska , nazwana na cześć belgijskiego matematyka Eugène Charlesa Catalana , jest powierzchnią prostoliniową , której wszystkie linie są równoległe do ustalonej płaszczyzny .

równania

Równanie wektorowe katalońskiej powierzchni jest podane przez

r = s ( u ) + v L ( u ),

gdzie r = s ( u ) jest krzywą przestrzenną , a L ( u ) jest wektorem jednostkowym rządzącym przy u = u . Wszystkie wektory L ( u ) są równoległe do tej samej płaszczyzny, zwanej płaszczyzną kierowniczą powierzchni. Można to scharakteryzować za pomocą warunku: produkt mieszany [ L ( u ), L' ( u ), L" ( u )] = 0. [1]

Równania parametryczne powierzchni katalońskiej to [2]

${\ Displaystyle x = f (u) + vi ( u),\quad y=g(u)+vj(u),\quad z=h(u)+vk(u)\,}$

Przypadki specjalne

Jeśli wszystkie rzędy powierzchni katalońskiej przecinają się z linią stałą , to powierzchnia ta nazywana jest stożkiem .

Catalan udowodnił, że helikoida i płaszczyzna były jedynymi minimalnymi powierzchniami rządzonymi .

Zobacz też

• Uogólniona helikoida

•   A. Gray, E. Abbena, S. Salamon, Nowoczesna geometria różniczkowa krzywych i powierzchni z Mathematica , wyd. Boca Raton, Floryda: CRC Press, 2006. [3] ( ISBN 978-1-58488-448-4 )
• „Powierzchnia katalońska” , Encyklopedia matematyki , EMS Press , 2001 [1994]
•   VY Rovenskii, Geometria krzywych i powierzchni z klonem [4] ( ISBN 978-0-8176-4074-3 )