Prawo rozdzielności między monadami

W teorii kategorii , abstrakcyjnej gałęzi matematyki , prawa dystrybucji między monadami są sposobem abstrakcyjnego wyrażenia, że ​​dwie struktury algebraiczne rozdzielają jedną na drugą.

Załóżmy, że ${\ Displaystyle (S, \ mu ^ {S}, \ eta ^ {S})}$ i ${\ Displaystyle (T, \ mu ^{T},\eta ^{T})}$ to dwie monady na kategorii C . Ogólnie rzecz biorąc, na funktorze złożonym ST nie ma naturalnej monady . Istnieje jednak naturalna struktura monady na funktorze ST , jeśli istnieje prawo rozdzielności monady S względem monady T .

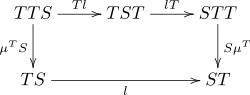
Formalnie prawo rozdzielności monady S względem monady T jest naturalną transformacją

${\ Displaystyle l: TS \ do ST}$

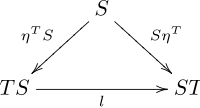
takie, że diagramy

        

        

dojeżdżać.

To prawo indukuje złożoną monadę ST z

• jako mnożenie: ${\ Displaystyle STST {\ xrightarrow {SlT}} SSTT {\ xrightarrow {\ mu ^ {S} \ mu ^ {T} }}ST}$ ,
• jako jednostka: ${\ Displaystyle 1 {\ xrightarrow {\ eta ^ {S} \ eta ^ {T}}} ST}$ .

Zobacz też

• prawo dystrybucji

•   Beck, Jon (1969). „Prawa dystrybucyjne”. Seminarium na temat trójek i teorii homologii kategorycznej, ETH 1966/67 . Notatki z wykładów z matematyki. Tom. 80. s. 119–140. doi : 10.1007/BFb0083084 . ISBN 978-3-540-04601-1 .

•   Barr, Michał ; Wells, Charles (1985). Toposy, trójki i teorie (PDF) . Springer-Verlag . ISBN 0-387-96115-1 . Zarchiwizowane od oryginału (PDF) w dniu 14.05.2011 r.
• Prawo dystrybucji w n Lab
•   Böhm, G. (2005). „Wewnętrzne bialgebroidy, struktury oplatające i rdzenie”. Struktury algebraiczne i ich reprezentacje . Współczesna matematyka. Tom. 376. s. 207–226. arXiv : math.QA/0311244 . ISBN 9780821836309 .
•   Brzeziński T.; Majid, S. (1998). „Wiązki koalgebry”. Kom. Matematyka fizyka . 191 (2): 467–492. ar Xiv : q-alg/9602022 . Bibcode : 1998CMaPh.191..467B . doi : 10.1007/s002200050274 . S2CID 189829500 .
•   Brzeziński Tomasz; Wisbauer, Robert (2003). Rdzenie i komoduły . Seria notatek z wykładów London Mathematical Society. Tom. 309. Cambridge University Press. ISBN 978-0-521-53931-9 .
•   Lis, TF; Markl, M. (1997). „Prawa dystrybucji, bialgebry i kohomologia”. Opery: Proceedings of Renaissance Conferences . Współczesna matematyka. Tom. 202. Amerykańskie Towarzystwo Matematyczne. s. 167–205. ISBN 9780821805138 .
• Brak, S. (2004). „Komponowanie rekwizytów” . aplikacja teoretyczna kategoria . 13 (9): 147–163.
• Brak, S.; Ulica, R. (2002). „Formalna teoria monad II” . J. Czysta aplikacja. Algebra . 175 (1–3): 243–265. doi : 10.1016/S0022-4049(02)00137-8 .
•   Markl, M. (1996). „Prawa dystrybucyjne i Koszulness” . Annales de l'Institut Fourier . 46 (2): 307–323. doi : 10.5802/aif.1516 . Zbl 0853.18005 .
• Ulica, R. (1972). „Formalna teoria monad” . J. Czysta aplikacja. Alg . 2 (2): 149–168. doi : 10.1016/0022-4049(72)90019-9 .
• Skoda, Z. (2004). „Prawa dystrybucji dla kategorii monoidalnych”. arXiv : matematyka/0406310 .
• — (2007). „Ekwiwariantne monady i ekwiwariantne windy a 2-kategoria praw dystrybucji”. arXiv : 0707.1609 [ matematyka.CT ].
• — (2008). „Bikategoria splotów”. arXiv : 0805.4611 [ matematyka. RA ].
•   — (2009). „Niektóre konstrukcje ekwiwariantne w geometrii nieprzemiennej”. matematyka gruzińska. J. _ 16 (1): 183–202. ar Xiv : 0811.4770 . doi : 10.1515/GMJ.2009.183 . S2CID 121946556 .
•   Wisbauer, R. (2008). „Algebry kontra węglagebry”. Aplikacja Kategoria Struktury . 16 (1–2): 255–295. doi : 10.1007/s10485-007-9076-5 . S2CID 8150337 .