Problem z kratą

W informatyce problemy kratowe są klasą problemów optymalizacyjnych związanych z obiektami matematycznymi zwanymi kratami . Przypuszczalna trudność takich problemów ma kluczowe znaczenie dla budowy bezpiecznych kryptosystemów opartych na sieciach : problemy z sieciami są przykładem problemów NP-trudnych , które okazały się trudne do przeciętnego przypadku , zapewniając przypadek testowy dla bezpieczeństwa algorytmów kryptograficznych. Ponadto niektóre problemy sieciowe, które są trudne w najgorszym przypadku, można wykorzystać jako podstawę dla wyjątkowo bezpiecznych schematów kryptograficznych. Zastosowanie najgorszego przypadku twardości w takich schematach czyni je jednymi z nielicznych schematów, które z dużym prawdopodobieństwem są bezpieczne nawet przed komputerami kwantowymi . W przypadku zastosowań w takich $)$ kraty w przestrzeni wektorowej często lub wolne moduły (często są ogólnie brane pod uwagę $.$

Dla wszystkich poniższych problemów załóżmy, że mamy (oprócz innych bardziej szczegółowych danych wejściowych) podstawę przestrzeni wektorowej V i normę N . Zwykle rozważaną normą jest norma euklidesowa L ² . Jednak inne normy (takie jak L ^p ) są również brane pod uwagę i pojawiają się w różnych wynikach. Niech oznacza długość najkrótszego niezerowego wektora w sieci L , to znaczy ${\ Displaystyle \ lambda (L)}$

${\ Displaystyle \ lambda (L) = \ min _ {v \ w L \ smallsetminus \ {\ mathbf {0} \}} \ | v \ | _ {N}.}$

Problem z najkrótszym wektorem (SVP)

To jest ilustracja problemu z najkrótszymi wektorami (wektory bazowe na niebiesko, najkrótszy wektor na czerwono).

W SVP baza przestrzeni wektorowej V i norma N (często L ² ) są podane dla sieci L i należy znaleźć najkrótszy niezerowy wektor w V , mierzony przez N , w L . Innymi słowy, algorytm powinien generować niezerowy wektor v taki, że ${\ Displaystyle N (v) = \ lambda (L)}$ .

W wersji z przybliżeniem γ SVP _γ należy znaleźć niezerowy wektor kratowy o długości co najwyżej ${\ Displaystyle \ gamma \ cdot \ lambda (L)}$ dla danego ${\ Displaystyle \ \ gamma \geq 1}$ .

Wyniki twardości

Wiadomo, że dokładna wersja problemu jest NP-trudna tylko dla losowych redukcji.

Natomiast odpowiedni problem w odniesieniu do jednolitej normy jest znany jako NP-trudny .

Algorytmy dla normy euklidesowej

Aby rozwiązać dokładną wersję SVP zgodnie z normą euklidesową, znanych jest kilka różnych podejść, które można podzielić na dwie klasy: algorytmy wymagające czasu superwykładniczego ( ${\ Displaystyle 2 ^ {\ omega (n)}}$ ) i ${\ Displaystyle \ operatorname {poli} (n)}$ pamięć i algorytmy wymagające zarówno wykładniczego czasu, jak i przestrzeni ( ${\ Displaystyle 2 ^ {\ Theta (n)}}$ ) w wymiarze kratowym. Pierwsza klasa algorytmów obejmuje przede wszystkim wyliczanie sieci i redukcję losowego próbkowania, podczas gdy druga obejmuje przesiewanie sieci, obliczanie komórki Woronoja sieci i dyskretne próbkowanie Gaussa. $wymagające wielomianowego$ do rozwiązywania dokładnych SVP działające w jednym czasie wykładniczym ( pamięci w wymiarze kratowym.

Aby rozwiązać wersję z przybliżeniem γ SVP $euklidesowej$ _dla normy , najbardziej znane podejścia opierają się na wykorzystaniu sieci . Dla dużych $znaleźć$ Lenstra Lenstra – Lovász (LLL) czasowym w wymiarze sieci. Dla mniejszych wartości ${\ displaystyle \ gamma}$ , powszechnie używany jest algorytm blokowy Korkine-Zolotarev (BKZ), w którym dane wejściowe do algorytmu (rozmiar bloku $określa$ złożoność czasową i jakość wyjściową: dla dużych współczynników przybliżenia ${\ displaystyle \ gamma}$$, wystarczy$ mały rozmiar bloku a algorytm szybko się kończy. Dla małych $}$ większych ${\ Displaystyle \ gamma$ są potrzebne do znalezienia wystarczająco krótkich wektorów sieciowych, a algorytm zajmuje więcej czasu, aby znaleźć rozwiązanie. Algorytm BKZ $\ displaystyle \ beta} beta }$ wykorzystuje dokładny algorytm SVP jako podprogram (działający w sieciach wymiarowych co najwyżej ), a jego ogólna złożoność jest ściśle związana z kosztami tych wywołań SVP w wymiarze ${$ .

GapSVP

Problem GapSVP _β polega na rozróżnieniu przypadków SVP, w których długość najkrótszego wektora jest co najwyżej $beta}$$można$ niż , gdzie β $\ displaystyle \$ stała funkcja wymiaru kraty ${\ displaystyle n}$ . Biorąc pod uwagę podstawę sieci, algorytm musi zdecydować, czy ${\ Displaystyle \ lambda (L) \ równoważnik 1}$ lub ${\ Displaystyle \ lambda (L)> \ beta}$ . Podobnie jak inne problemy z obietnicami , algorytm może popełniać błędy we wszystkich innych przypadkach.

Jeszcze inną wersją problemu jest GapSVP _{ζ, γ} dla niektórych funkcji ${\ Displaystyle \ zeta, \ gamma}$ . Dane wejściowe do $algorytmu$$to$ liczba . Zapewnia się, że wszystkie wektory w ortogonalizacji Grama-Schmidta mają długość co najmniej 1 i że ${\ Displaystyle \ lambda (L (B)) \ równoważnik \ zeta (n)}$ i że ${\ Displaystyle 1 \ równoważnik d \ równoważnik \ zeta (n) / \ gamma (n)}$ gdzie jest wymiarem ${\ displaystyle n} .$ Algorytm musi zaakceptować, jeśli ${\ Displaystyle \ lambda (L (B)) \ równoważnik d}$ i odrzucić, jeśli ${\ Displaystyle \ lambda (L (B)) \ geq \ gamma (n). d}$ . W przypadku dużych $($ tj. _ζ $\ Displaystyle \ zeta (n)> 2 ^ {n/2}} )$ problem jest równoważny z GapSVP , ponieważ wykonano przetwarzanie wstępne użycie algorytmu LLL sprawia $)$ że ​​drugi warunek (a co za tym idzie jest zbędny.

Problem z najbliższym wektorem (CVP)

To jest ilustracja problemu z najbliższymi wektorami (wektory bazowe na niebiesko, wektor zewnętrzny na zielono, najbliższy wektor na czerwono).

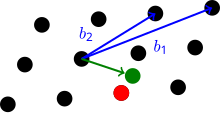
W CVP baza przestrzeni wektorowej V i metryka M (często L ² ) są podane dla sieci L , jak również wektor v w V , ale niekoniecznie w L . Pożądane jest znalezienie wektora w L najbliższego v (mierzonego przez M ). W przybliżonej wersji CVP $\ displaystyle \ gamma}$ należy znaleźć wektor kratowy w odległości co najwyżej _{ ${\ displaystyle \ gamma}$ .

Związek z SVP

Najbliższy problem wektorowy jest uogólnieniem problemu najkrótszego wektora. Łatwo jest pokazać, że mając wyrocznię dla CVP _γ (zdefiniowaną poniżej), można rozwiązać SVP _γ , zadając pewne zapytania do wyroczni. Naiwna metoda znajdowania najkrótszego wektora przez wywołanie wyroczni CVP _γ w celu znalezienia wektora najbliższego 0 nie działa, ponieważ 0 samo w sobie jest wektorem kratowym, a algorytm mógłby potencjalnie wyprowadzić 0.

Redukcja z SVP _γ do CVP _γ jest następująca: Załóżmy, że wejście do SVP _γ jest podstawą sieci ${\ Displaystyle B = [b_ {1}, b_{2},\ldots ,b_{n}]}$ . Rozważmy podstawę ${\ Displaystyle B ^ {i} = [b_ {1}, \ ldots, 2b_ {i}, \ ldots, b_ {n}]} i niech x ja {\ Displaystyle$ x_ $}}$ będzie wektorem zwróconym przez CVP _γ (Bi ^, bi ₎ . Twierdzenie jest takie, że najkrótszy wektor $zbiorze$ wektorem

Wyniki twardości

Goldreich i in. wykazało, że każda twardość SVP implikuje taką samą twardość dla CVP. Używając narzędzi PCP , Arora i in. pokazał, że CVP jest trudny do przybliżenia w ramach czynnika ${\ Displaystyle 2 ^ {\ log ^ {1- \ epsilon} (n)}},$ chyba że ${\ Displaystyle \ nazwa operatora {NP} \ subseteq \ nazwa operatora {DTIME} (2 ^ {\ nazwa operatora {poly} (\ log n)})}$ . Dinur i in. wzmocniłem to, podając wynik twardości NP z ${\ Displaystyle \ epsilon = (\ log \ log n) ^ {c}}$ dla ${\ Displaystyle c <1 /2}$ .

Dekodowanie sfery

systemach komunikacji bezprzewodowej z wieloma wejściami i wyjściami ( MIMO ) (dla sygnałów kodowanych i niekodowanych). W tym kontekście nazywa się to dekodowaniem sferycznym ze względu na promień używany w wielu rozwiązaniach CVP.

Została ona zastosowana w dziedzinie rozdzielczości całkowitoliczbowej GNSS (GPS) w fazie nośnej. W tej dziedzinie nazywa się to metodą LAMBDA . W tym samym polu ogólny problem CVP jest określany jako liczba całkowita najmniejszych kwadratów .

GapCVP

Ten problem jest podobny do problemu GapSVP. W przypadku GapSVP _β dane wejściowe składają się z podstawy sieci i wektora, a algorytm musi odpowiedzieć, czy zachodzi jedno z poniższych stwierdzeń: ${\ displaystyle v}$

• istnieje taki wektor kratowy, że odległość między nim $wynosi$ co najwyżej 1.
• $się$$sieci znajduje$ w odległości większej od .

Odwrotnym warunkiem jest to, że najbliższy wektor sieci znajduje się w odległości ${\ Displaystyle 1 <\ lambda (L) \ równoważnik \ beta}$ , stąd nazwa Gap CVP.

Znane wyniki

Problem jest trywialnie zawarty w NP dla dowolnego współczynnika przybliżenia.

Schnorr w 1987 roku wykazał, że deterministyczne algorytmy czasu wielomianowego mogą rozwiązać problem dla ${\ Displaystyle \ beta = 2 ^ {O (n (\ log \log n)^{2}/\log n)}}$ . Ajtai i in. pokazał, że algorytmy probabilistyczne mogą osiągnąć nieco lepszy współczynnik aproksymacji ${\ Displaystyle \ beta = 2 ^ {O (n \ log \ log n/\ log n)}}$ .

W 1993 Banaszczyk wykazał, że GapCVP _n jest w ${\ Displaystyle {\ mathsf {NP \ cap coNP}}}$ . W 2000 roku Goldreich i Goldwasser wykazali, że $.$ problem w $problem$ 2005 roku Aharonov i Regev wykazali, że dla pewnej stałej z ${\ Displaystyle \ beta = c {\ sqrt {n}}}$ jest w ${\ Displaystyle {\ mathsf {NP \ cap coNP}}}$ .

Dla dolnych granic Dinur i in. $_$ problem _

Najkrótszy problem wektorów niezależnych (SIVP)

Biorąc pod uwagę siatkę L o wymiarze n , algorytm musi wyprowadzać n liniowo niezależnych ${\ Displaystyle v_ {1}, v_ {2}, \ ldots, v_ {n}}$ tak, że ${\ Displaystyle \ max \|v_ {i} \|\ równoważnik \ max _ {B} \|b_ {i} \|} gdzie prawa$ strona uwzględnia wszystkie podstawy ${\ Displaystyle B = \ {b_ {1}, \ ldots, b_ {n} \}}$ kraty.

W $wektorów$ wersji, biorąc pod uwagę siatkę L o wymiarze n , znajdź n liniowo niezależnych v $\ displaystyle v_ {1}, v_ {2}, \ ldots, v_ {n}}$ długości ${\ Displaystyle \ max \| v_ {i} \|\ równoważnik \ gamma \ lambda _ {n} (L)$ } ${\ Displaystyle \ lambda _ {n} (L)}$ jest ${\ Displaystyle n}$ 'tym kolejnym minimum ${\ Displaystyle L}$ .

Dekodowanie ograniczonej odległości

Ten problem jest podobny do CVP. Biorąc $pod uwagę wektor$ od sieci wynosi co najwyżej wyprowadzić najbliższy mu wektor sieci.

Problem z promieniem pokrycia

Biorąc pod uwagę podstawę sieci, algorytm musi znaleźć największą odległość (lub w niektórych wersjach jej przybliżenie) od dowolnego wektora do sieci.

Problem z najkrótszą bazą

Wiele problemów staje się łatwiejszych, jeśli baza wejściowa składa się z krótkich wektorów. Algorytm, który rozwiązuje problem najkrótszej podstawy $B'}$ biorąc pod uwagę podstawę sieci , wyprowadzić równoważną podstawę taką $,$ że długość najdłuższego wektora w $}$${\ displaystyle B$ jest możliwie najkrótszy.

wersji aproksymacyjnej SBP _γ polega na znalezieniu podstawy, której najdłuższy wektor jest co najwyżej $.$ dłuższy niż najdłuższy wektor w najkrótszej podstawie

Zastosowanie w kryptografii

Główny artykuł: Kryptografia oparta na sieciach

Średnia twardość przypadków stanowi podstawę dla dowodów bezpieczeństwa dla większości schematów kryptograficznych. Jednak dowody eksperymentalne sugerują, że większość problemów NP-trudnych nie ma tej właściwości: prawdopodobnie są one trudne tylko w najgorszym przypadku. Przypuszczano lub udowodniono, że wiele problemów z sieciami jest średnio trudnych, co czyni je atrakcyjną klasą problemów, na których można oprzeć schematy kryptograficzne. Co więcej, do stworzenia bezpiecznych schematów kryptograficznych wykorzystano twardość najgorszego przypadku niektórych problemów sieciowych. Zastosowanie najgorszego przypadku twardości w takich schematach czyni je jednymi z nielicznych schematów, które z dużym prawdopodobieństwem są bezpieczne nawet przed komputerami kwantowymi .

Powyższe problemy sieciowe są łatwe do rozwiązania, jeśli algorytm ma „dobrą” podstawę. Algorytmy redukcji sieci mają na celu, biorąc pod uwagę podstawę sieci, wygenerowanie nowej bazy składającej się ze stosunkowo krótkich, prawie ortogonalnych wektorów. Algorytm redukcji podstawy sieci Lenstra – Lenstra – Lovásza (LLL) był wczesnym wydajnym algorytmem dla tego problemu, który mógł generować prawie zredukowaną podstawę sieci w czasie wielomianowym. Algorytm ten i jego dalsze udoskonalenia zostały wykorzystane do złamania kilku schematów kryptograficznych, ustanawiając jego status bardzo ważnego narzędzia w kryptoanalizie. Sukces LLL na danych eksperymentalnych doprowadził do przekonania, że ​​redukcja sieci może być łatwym problemem w praktyce. Jednak to przekonanie zostało zakwestionowane, gdy pod koniec lat 90. uzyskano kilka nowych wyników dotyczących problemów z twardością sieci, poczynając od wyniku Ajtai .

W swoich przełomowych artykułach Ajtai wykazał, że problem SVP był NP-trudny i odkrył pewne powiązania między złożonością najgorszego przypadku a złożonością przypadku średniego niektórych problemów sieciowych. Opierając się na tych wynikach, Ajtai i Dwork stworzyli kryptosystem z kluczem publicznym , którego bezpieczeństwo można było udowodnić przy użyciu tylko najgorszej twardości określonej wersji SVP, co czyni go pierwszym wynikiem, w którym wykorzystano twardość najgorszego przypadku do stworzenia bezpiecznych systemów.

Zobacz też

• Nauka z błędami
• Problem rozwiązania krótkich liczb całkowitych

Dalsza lektura

• Agrell, E.; Eriksson, T.; Vardy, A.; Zeger, K. (2002). „Wyszukiwanie najbliższego punktu w kratach” . IEEE Trans. Inf. Teoria . 48 (8): 2201–2214. doi : 10.1109/TIT.2002.800499 .
•    Micciancio, Daniele (2001). „Najkrótszy problem wektorowy jest {NP} trudny do przybliżenia w obrębie pewnej stałej” . SIAM Journal o informatyce . 30 (6): 2008–2035. CiteSeerX 10.1.1.93.6646 . doi : 10.1137/S0097539700373039 . S2CID 42794945 .
•   Nguyen, Phong Q.; Stern, Jacques (2000). „Redukcja kraty w kryptologii: aktualizacja” . Materiały z 4. Międzynarodowego Sympozjum Algorytmicznej Teorii Liczb . Springer-Verlag. s. 85–112. ISBN 978-3-540-67695-9 .