Przepływ punktu stagnacji

W dynamice płynów przepływ w punkcie stagnacji reprezentuje przepływ płynu w bezpośrednim sąsiedztwie punktu stagnacji (lub linii stagnacji), za pomocą którego punkt stagnacji (lub linia) jest identyfikowany dla przepływu potencjalnego lub przepływu nielepkiego. Przepływ w szczególności uwzględnia klasę punktów stagnacji zwanych punktami siodłowymi, w których przychodzące linie prądu są odchylane i kierowane na zewnątrz w innym kierunku; ugięcia linii prądu są kierowane przez separatory. Przepływ w sąsiedztwie punktu lub linii spiętrzenia można ogólnie opisać za pomocą przepływu potencjalnego teoria, chociaż efektów lepkości nie można pominąć, jeśli punkt stagnacji leży na twardej powierzchni.

Przepływ w punkcie stagnacji bez stałych powierzchni

Kiedy dwa strumienie o charakterze dwuwymiarowym lub osiowosymetrycznym zderzają się ze sobą prostopadle, powstaje płaszczyzna stagnacji, w której napływające strumienie są kierowane stycznie na zewnątrz; tak więc na płaszczyźnie stagnacji składowa prędkości normalna do tej płaszczyzny wynosi zero, podczas gdy składowa styczna jest niezerowa. W sąsiedztwie punktu stagnacji można opisać lokalny opis pola prędkości.

Ogólne trójwymiarowe pole prędkości

$,$ od współrzędnych, którą można opisać ${\ Displaystyle (v_ {x}, v_ {y}, v_ {z})}$ składowymi w następujący sposób

${\ Displaystyle v_ {x} = \ alfa x, \ quad v_ {y} = \ beta y, \ quad v_ {z} = \ gamma z }$

gdzie ${\ Displaystyle (\ alfa, \ beta, \ gamma)}$ to stałe określane jako szybkości odkształcenia; $,$ ponieważ równanie ciągłości wymaga tylko dwie z trzech stałych są Założymy, że przepływ jest skierowany w stronę punktu stagnacji w ${\ Displaystyle \ gamma <0 \ równoważnik \ alfa}$${\ displaystyle z}$ kierunku i od punktu stagnacji w kierunku ${\ displaystyle x}$ . Bez utraty ogólności można założyć, że ${\ Displaystyle \ beta \ geq \ alpha}$ . Pole przepływu można podzielić na różne typy na podstawie jednego parametru

${\ Displaystyle \ lambda = {\ Frac {\ alfa - \ beta} {\ alfa + \ beta}}}$

Planarny przepływ w punkcie stagnacji

Dwuwymiarowy przepływ w punkcie stagnacji należy do przypadku . ${\ Displaystyle \ beta = 0 \, (\ lambda = 1)}$ . Pole przepływu jest opisane w następujący sposób

${\ Displaystyle v_ {x} = kx, \ quad v_ {z} = - kz}$

gdzie pozwalamy ${\ Displaystyle k = \ alfa = - \ gamma > 0}$ . To pole przepływu zostało zbadane już w 1934 roku przez GI Taylora . W laboratorium to pole przepływu jest tworzone za pomocą aparatu czteromilimetrowego, chociaż te pola przepływu są wszechobecne w przepływach turbulentnych.

Osiowosymetryczny przepływ w punkcie stagnacji

Osiowosymetryczny przepływ w punkcie stagnacji odpowiada ${\ Displaystyle \ alpha = \ beta \, (\ lambda = 0)}$ . Pole przepływu można po prostu opisać w cylindrycznym układzie współrzędnych $0,v_{z})}$ v $Displaystyle$${r$ w następujący sposób

${\ Displaystyle v_ {r} = kr, \ quad v_ {z} = -2kz}$

gdzie pozwalamy ${\ Displaystyle k = \ alfa = \ beta = - \ gamma / 2> 0}$ .

Radialne przepływy stagnacyjne

W radialnych przepływach stagnacyjnych zamiast punktu stagnacyjnego mamy koło stagnacyjne, a płaszczyznę stagnacyjną zastępuje cylinder stagnacyjny. Promieniowy przepływ stagnacji jest opisany za pomocą cylindrycznego układu współrzędnych ${\ Displaystyle (r, z)}$ ze składowymi prędkości ${\ Displaystyle (v_ {r}, v_ {z})}$ następująco

${\ Displaystyle v_ {r} = - k \ lewo (r - {\ Frac {r_ {s} ^ {2}} {r }}\right),\quad v_{z}=2kz}$

gdzie $położeniem$ cylindra stagnacji

Przepływ Hiemenza

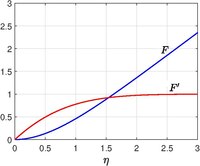
Dwuwymiarowy przepływ w punkcie stagnacji

Przepływ spowodowany obecnością stałej powierzchni w $punkcie spiętrzenia został opisany po raz pierwszy przez Karla Hiemenza w 1911 r.,$ obliczenia numeryczne rozwiązań zostały później ulepszone przez Leslie Howarth . Znanym przykładem zastosowania przepływu Hiemenza jest przednia linia stagnacji, która występuje w przepływie przez okrągły cylinder.

Stała powierzchnia leży na ${\ displaystyle xy}$ . Zgodnie z teorią przepływu potencjalnego, ruch płynu opisany za pomocą funkcji strumienia $Displaystyle$ składowych prędkości $(v_ {x}, 0, v_ {z} )}$ są podane przez

${\ Displaystyle \ psi = kxz, \ quad v_ {x} = kx, \ quad v_ {z} = - kz.}$

Linia stagnacji dla tego przepływu to ${\ Displaystyle (x, y, z) = (0, y, 0)}$ . $ścianie$ prędkości jest różna od zera na powierzchni stałej, co wskazuje, że powyższe pole prędkości nie spełnia warunku brzegowego braku poślizgu na Aby znaleźć składowe prędkości, które spełniają warunek brzegowy braku poślizgu, przyjmuje się następującą postać

${\ Displaystyle \ psi = {\ sqrt {\ nu k}} x F (\ eta), \ quad \ eta = {\ Frac {z} {\ sqrt {\nu /k}}}}$

gdzie jest $lepkością$ i jest charakterystyczną grubością, przy której $.$ lepkości Istnienie stałej wartości grubości efektów lepkich wynika z konkurencyjnej równowagi między konwekcją płynu skierowaną w stronę powierzchni ciała stałego a dyfuzją lepkości skierowaną od powierzchni. Zatem wirowość wytwarzana na powierzchni ciała stałego może rozprzestrzeniać się tylko na odległości rzędu ${\ Displaystyle {\ sqrt {\ nu / k}}}$ ; analogiczne sytuacje przypominające to zachowanie występują w asymptotycznym profilu ssania i przepływie wirowym von Kármána . Składowe prędkości, ciśnienie i równania Naviera-Stokesa stają się wtedy

${\ Displaystyle v_ {x} = kxF' ,\quad v_{z}=-{\sqrt {\nu k}}F,\quad {\frac {p_{o}-p}{\rho }}={\frac {1}{2}}k ^{2}x^{2}+k\nu F'+{\frac {1}{2}}k\nu F^{2}}$

${\ Displaystyle F ''' + FF ''-F' ^ {2} + 1 = 0}$

Wymagania, które ${\ Displaystyle (v_ {x}, v_ {z}) = (0,0)}$ w ${\ Displaystyle z = 0}$ i że ${\ Displaystyle v_ {x} \ rightarrow kx}$ jak ${\ Displaystyle z \ rightarrow \ infty}$ przekładać na

${\ Displaystyle F (0) = 0, \ F' (0) = 0, F '(\ infty) = 1.}$

Warunek dla $jako$ może $być$ określony i jest uzyskiwany Sformułowany tu problem jest szczególnym przypadkiem warstwy granicznej Falknera-Skana . Rozwiązanie można otrzymać z całkowania numerycznego i pokazano na rysunku. Asymptotyczne zachowania dla dużych to ${\ Displaystyle \ eta \ rightarrow \ infty}$

${\ Displaystyle F \ sim \ eta -0,6479, \ quad v_ {x} \ sim kx, \quad v_{z}\sim -k(z-\delta ^{*}),\quad \delta ^{*}=0,6479\delta }$

gdzie $_$ grubością . _

Przepływ punktowy z przesuwającą się ścianą

$,$$osi$ ściana przesuwa się ze stałą prędkością wzdłuż został rozwiązany przez Rotta (1956). Problem ten opisuje przepływ w sąsiedztwie przedniej linii spiętrzenia występujący w przepływie przez obracający się cylinder. Wymagana funkcja strumienia to

${\ Displaystyle \ psi = {\ sqrt {\ nu k}} xF (\ eta) + U \ delta \ int _ {0} ^{\eta}G(\eta)d\eta}$

spełnia funkcja ${\ Displaystyle G (\ eta)}$

${\ Displaystyle G'' + FG'-F'G = 0, \ quad G (0) = 1, \ quad G(\infty)=0}$

Rozwiązanie powyższego równania jest dane przez ${\ Displaystyle G (\ eta) = F '' (\ eta) / F'' (0).}$

Ukośny przepływ w punkcie stagnacji

$się ukośnie, przepływ$ jest potencjalny, ale ma stałą wirowość . Odpowiednią funkcję strumienia dla ukośnego przepływu w punkcie stagnacji podaje wzór

${\ Displaystyle \ psi = kxz + {\ Frac {1} {2}} \ zeta _ {o} z ^ {2}}$

Efekty lepkości spowodowane obecnością litej ściany badali Stuart (1959), Tamada (1979) i Dorrepaal (1986). W ich podejściu funkcja strumienia przybiera formę

${\ Displaystyle \ psi = {\ sqrt {\ nu k}} xF (\ eta) + \ zeta _ {o} \ delta ^{2}\int _{0}^{\eta }H(\eta )d\eta }$

gdzie funkcja ${\ Displaystyle H (\ eta)}$

${\ Displaystyle H'' + FH'-F'H = 0, \ quad H (0) = 0, \ quad H'(\infty )=1}$ .

Przepływ Homanna

Homann flow z wtryskiem

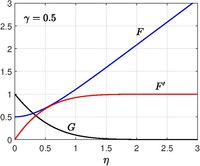
Przepływ Homann z odsysaniem

Rozwiązanie osiowosymetrycznego przepływu w punkcie spiętrzenia w obecności litej ściany zostało po raz pierwszy otrzymane przez Homanna (1936). Typowym przykładem tego przepływu jest punkt stagnacji do przodu, który pojawia się w przepływie obok kuli. Paul A. Libby (1974) (1976) rozszerzył pracę Homanna, umożliwiając litej ścianie przesuwanie się wzdłuż własnej płaszczyzny ze stałą prędkością i umożliwiając stałe zasysanie lub wstrzykiwanie na stałą powierzchnię.

Rozwiązanie tego problemu uzyskuje się w cylindrycznym układzie współrzędnych ${\ Displaystyle (r, \ theta, z)}$ przez wprowadzenie

${\ Displaystyle \ eta = {\ Frac {z} {\ sqrt {\ nu / k}}}, \ quad \ gamma = - {\ Frac {V} {2 {\ sqrt {k \ \ nu }}}},\quad v_{r}=krF'(\eta )+U\cos \theta G(\eta ),\quad v_{\theta }=-U\sin \theta G(\eta ) ,\quad v_{z}=-2{\sqrt {k\nu }}F(\eta )}$

gdzie jest prędkością $translacji$ ściany i jest prędkością $)$ na ścianie. Problem jest osiowosymetryczny tylko wtedy, gdy ${\ displaystyle U = 0}$ . Ciśnienie jest podane przez

${\ Displaystyle {\ Frac {pp_ {o}} {\ rho}} = - {\ Frac {1 }{2}}k^{2}r^{2}-2k\nu (F^{2}+F')}$

Równania Naviera-Stokesa redukują się następnie do

${\ Displaystyle {\ rozpocząć {wyrównane} F'''+ 2FF''-F' ^ {2 }+1&=0,\\G''+2FG'-F'G&=0\end{wyrównane}}}$

wraz z warunkami brzegowymi,

${\ Displaystyle F (0) = \ gamma \ quad F '(0 )=0,\quad F'(\infty )=1,\quad G(0)=1,\quad G(\infty )=0.}$

Kiedy ${\ displaystyle U = V = 0}$ , klasyczny problem Homanna zostaje przywrócony.

Płaskie przeciwprądy

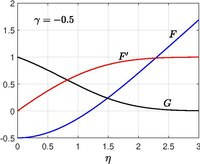
Strumienie wychodzące z dysz szczelinowych tworzą punkt stagnacji pomiędzy nimi, zgodnie z teorią potencjału. Przepływ w pobliżu punktu spiętrzenia można badać za pomocą rozwiązania samopodobnego. Ta konfiguracja jest szeroko stosowana w ze spalaniem . Wstępne badanie zderzających się przepływów stagnacyjnych jest dziełem CY Wanga. $_$ oznaczymy płynący z przeciwnego kierunku zderzają się i załóżmy, że te dwa płyny nie mieszają się, a interfejs (znajdujący się $)$ płaski. Prędkość jest dana przez

${\ Displaystyle u_ {1} = k_ {1} x \ quad v_ {1} = -k_{1}y,\quad u_{2}=k_{2}x,\quad v_{2}=-k_{2}y}$

gdzie ${\ Displaystyle k_ {1}, \ k_ {2}}$ to szybkości odkształcania płynów. Na granicy faz prędkości, naprężenia styczne i ciśnienie muszą być ciągłe. Wprowadzenie transformacji samopodobnej,

${\ Displaystyle \ eta _ {1} = {\ sqrt {\ Frac {\ nu _ { 1}}{k_{1}}}}y,\quad u_{1}=k_{1}xF_{1}',\quad v_{1}=-{\sqrt {\nu _{1}k_{ 1}}}F_{1}}$

${\ Displaystyle \ eta _ {2} = {\ sqrt {\ Frac {\ nu _ {2}} {k_ {2}}}} y, \quad u_{2}=k_{2}xF_{2}',\quad v_{2}=-{\sqrt {\nu _{2}k_{2}}}F_{2}}$

równania wyników,

${\ Displaystyle F_ {1} ''' + F_ {1} F_ {1} '' - F_ {1} ' ^ {2} + 1 = 0, \ quad {\ Frac {p_ {o1} - p_ {1 }}{\rho _{1}}}={\frac {1}{2}}k_{1}^{2}x^{2}+k_{1}\nu _{1}F_{1} '+{\frac {1}{2}}k_{1}\nu _{1}F_{1}^{2}}$

${\ Displaystyle F_ {2} ''' + F_ {2} F_ {2} '' - F_ {2} ' ^ {2} + 1 = 0, \ quad {\ Frac {p_ {o2} - p_ {2 }}{\rho _{2}}}={\frac {1}{2}}k_{2}^{2}x^{2}+k_{2}\nu _{2}F_{2} '+{\frac {1}{2}}k_{2}\nu _{2}F_{2}^{2}.}$

Stan braku penetracji na granicy faz i warunek swobodnego strumienia daleko od płaszczyzny stagnacji stają się

${\ Displaystyle F_ {1} (0) = 0, \ quad F_ {1} '(\infty )=1,\quad F_{2}(0)=0,\quad F_{2}'(-\infty)=1.}$

Ale równania wymagają jeszcze dwóch warunków brzegowych. η ${\ Displaystyle \ eta = 0}$ , prędkości styczne ${\ Displaystyle u_ {1} = u_ {2}}$ naprężenie styczne ${\ Displaystyle \ rho _ {1} \ nu _ {1} \ częściowe u_ {1} / \ częściowe y = \ rho _ {2} \ nu _ {2} \ częściowe u_ { 2}/\częściowe y}$$_$ ciśnienie _ Dlatego,

${\ Displaystyle {\ rozpocząć {wyrównane} k_ {1} F_ {1} '(0) & = k_ {2} F_ {2} ' (0), \\\ rho _ {1} {\ sqrt {\ nu _{1}k_{1}^{3}}}F_{1}''(0)&=\rho _{2}{\sqrt {\nu _{2}k_{2}^{3}} }F_{2}''(0),\\p_{o1}-\rho_{1}\nu _{1}k_{1}F_{1}'(0)&=p_{o2}-\ rho _{2}\nu _{2}k_{2}F_{2}'(0).\end{wyrównane}}}$

gdzie ${1} ^ {2} = \ rho _ {2} k_ {2} ^ {2}}}$ k_ ) Jest używane. Oba $_$ _ _ _ Trzecie równanie to wyznaczenie zmiany ciśnienia zewnętrznego ${\ displaystyle p_ {o1} -p_ {o2}}$ ze względu na wpływ lepkości. Są więc tylko dwa parametry, którymi rządzi przepływ, czyli tzw

${\ Displaystyle \ Lambda = {\ Frac {k_ {1}} {k_ {2}}} = \ lewo ({{ \frac {\rho _{2}}{\rho _{1}}}\right)^{1/2},\quad \Gamma ={\frac {\nu _{2}}{\nu _{ 1}}}}$

wówczas staną się warunki brzegowe

${\ Displaystyle F_ {1} '(0) = \ Lambda F_ {2}' (0), \ quad F_{1}''(0)={\sqrt {\frac {\Gamma}} {\Lambda}}}F_{2}''(0)}$ .