Schemat motyla

Ten artykuł dotyczy diagramów motylkowych w algorytmach FFT. Aby zapoznać się z diagramami plam słonecznych, zobacz Cykl słoneczny .

Wykres przepływu sygnału łączący wejścia x (po lewej) z wyjściami y , które od nich zależą (po prawej) dla kroku „motylkowego” radix-2 Cooley – Tukey FFT. Diagram ten przypomina motyla (jak u pokazanego dla porównania motyla morpho ), stąd nazwa, chociaż w niektórych krajach nazywany jest również diagramem klepsydry.

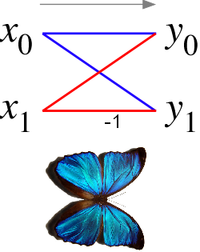
W kontekście szybkich algorytmów transformaty Fouriera motyl jest częścią obliczeń, która łączy wyniki mniejszych dyskretnych transformat Fouriera (DFT) w większą DFT lub odwrotnie (podział większej DFT na podtransformacje). Nazwa „motyl” pochodzi od kształtu diagramu przepływu danych w przypadku radix-2, jak opisano poniżej. Uważa się, że najwcześniejsze wystąpienie tego terminu w druku pojawiło się w MIT Subhranila Majumdera z 1969 roku . Tę samą strukturę można znaleźć również w algorytmie Viterbiego , służącym do znajdowania najbardziej prawdopodobnej sekwencji stanów ukrytych.

Najczęściej termin „motyl” pojawia się w kontekście algorytmu Cooley-Tukey FFT , który rekurencyjnie rozkłada DFT o złożonym rozmiarze n = rm na r mniejszych transformat o rozmiarze m , gdzie r jest „podstawą” transformacji. Te mniejsze DFT są następnie łączone za pomocą motyli o rozmiarze r , które same są DFT o rozmiarze r (wykonywane m razy na odpowiednich wyjściach podprzekształceń) wstępnie pomnożone przez pierwiastki jedności (znane jako współczynniki twiddle ). (To jest przypadek „dziesiątkowania w czasie”; można również wykonać kroki w odwrotnej kolejności, znane jako „dziesiątkowanie częstotliwości”, w którym motyle są pierwsze i są mnożone przez współczynniki twiddle. Zobacz także artykuł Cooley – Tukey FFT .)

Schemat motyla Radix-2

₀₀ W przypadku algorytmu radix-2 Cooley-Tukey motyl jest po prostu DFT o rozmiarze-2, który przyjmuje dwa wejścia ( x , x ₁ ) (odpowiednie wyjścia dwóch podprzekształceń) i daje dwa wyjścia ( y , y ₁ ) według wzoru (bez uwzględnienia współczynników twiddle ):

${\ Displaystyle y_ {0} = x_ {0} + x_ {1} \,}$

${\ displaystyle y_ {1} = x_ {0} -x_ {1}. \,}$

₀₀ Jeśli narysujemy diagram przepływu danych dla tej pary operacji, linie ( _x , x1 ) do ( y , y1 ) przecinają się i przypominają skrzydła motyla , stąd _nazwa (patrz także ilustracja po prawej).

Decymacja w czasie radix-2 FFT dzieli długość- N DFT na dwie długości- N /2 DFT, po których następuje etap łączenia składający się z wielu operacji motylkowych.

  Dokładniej, algorytm FFT radix-2 z dziesiątkowaniem w czasie na wejściach n = 2   ^p w odniesieniu do prymitywnego n -tego pierwiastka jedności ${\ Displaystyle \ omega _ {n }^{k}=e^{-{\frac {2\pi ik}{n}}}}$ opiera się na O( n log ₂ n ) motylach postaci:

${\ Displaystyle y_ {0} = x_ {0} + x_ {1} \ omega _ {n} ^ {k} \,}$

${\ Displaystyle y_ {1} = x_ {0} -x_ {1} \ omega _ {n} ^ {k}, \,}$

gdzie k jest liczbą całkowitą zależną od obliczanej części transformacji. Podczas gdy odpowiednią transformację odwrotną można wykonać matematycznie, zastępując ω przez ω ^-1 (i ewentualnie mnożąc przez ogólny współczynnik skali, w zależności od konwencji normalizacji), można również bezpośrednio odwrócić motyle:

${\ Displaystyle x_ {0} = {\ Frac {1} {2}} (y_ {0} + y_ {1}) \,}$

${\ Displaystyle x_ {1} = {\ Frac {\ omega _ {n} ^ {-k}} {2}} (y_ {0} -y_ {1}), \,}$

odpowiadający algorytmowi FFT z decymacją w częstotliwości.

Inne zastosowania

Motyl może być również użyty do poprawy losowości dużych tablic częściowo losowych liczb, poprzez doprowadzenie każdego 32- lub 64-bitowego słowa do kontaktu przyczynowego z każdym innym słowem za pomocą pożądanego algorytmu mieszającego, tak aby zmiana dowolnego bitu miała możliwość zmiany wszystkich bitów w dużej tablicy.

Zobacz też

• Schemat matematyczny
• Lemat Zassenhausa
• Wykres przepływu sygnału

Linki zewnętrzne

• wyjaśnienie diagramów FFT i motyli .
• diagramy motylkowe różnych implementacji FFT (Radix-2, Radix-4, Split-Radix) .