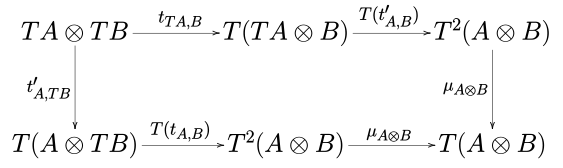Silna monada

W teorii kategorii silna monada nad kategorią monoidalną ( C , ⊗, I) jest monadą ( T , η, μ) wraz z naturalną transformacją t _A,B : A ⊗ TB → T ( A ⊗ B ), zwaną ( wytrzymałość na rozciąganie ) , taka jak na diagramach

, ,

, i

dojazdy dla każdego obiektu A , B i C (patrz Definicja 3.2 w ).

Jeśli kategoria monoidalna ( C , ⊗, I) jest domknięta , to silna monada jest tym samym, co monada wzbogacona w C.

Przemienne silne monady

Dla każdej silnej monady T w symetrycznej kategorii monoidalnej można zdefiniować naturalną transformację kosztowo -siłową

${\ Displaystyle t'_ {A, B} = T ( \gamma _{B,A})\circ t_{B,A}\circ \gamma _{TA,B}:TA\otimes B\to T(A\otimes B)}$ .

, że silna monada T jest przemienna , gdy diagram

dojazdy do pracy dla wszystkich obiektów i ZA {\ displaystyle $}$ i ${\ displaystyle B}$ .

Interesującym faktem dotyczącym przemiennych silnych monad jest to, że są one „takie same jak” symetryczne monady monodyczne . bardziej wyraźnie,

• przemienna silna monada ${\ Displaystyle (T, \ eta, \ mu, t)}$ definiuje symetryczną monadę monoidalną ${\ Displaystyle (T, \ eta) ,\mu ,m)}$ przez

${\ Displaystyle m_ {A, B} = \ mu _ {A \ otimes B} \ circ Tt'_ {A, B} \ circ t_ {TA,$

• i odwrotnie, symetryczna monodyczna monada ${\ Displaystyle (T, \ eta, \ mu, m)}$ definiuje moc przemienną monada ${\ Displaystyle (T, \ eta, \ mu, t)}$ przez

${\ Displaystyle t_ {A,B}=m_{A,B}\circ (\eta _{A}\otimes 1_{TB}):A\otimes TB\to T(A\otimes B)}$

a konwersja między jedną a drugą prezentacją jest bijektywna.

•   Andersa Kocka (1972). „Silne funktory i monady monoidalne” (PDF) . Archiv der Mathematik . 23 : 113–120. doi : 10.1007/BF01304852 . S2CID 13246783 .
•   Jean Goubault-Larrecq, Sławomir Lasota i David Nowak (2005). „Relacje logiczne dla typów monadycznych”. Struktury matematyczne w informatyce . 18 (6): 1169. arXiv : cs/0511006 . doi : 10.1017/S0960129508007172 . S2CID 741758 .