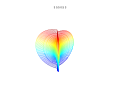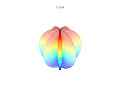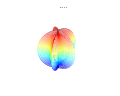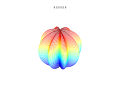Super formuła

Superformuła jest uogólnieniem superelipsy i została zaproponowana przez Johana Gielisa około 2000 roku. Gielis zasugerował, że formuła może być używana do opisu wielu złożonych kształtów i krzywych występujących w przyrodzie. Gielis złożył wniosek patentowy dotyczący syntezy wzorców generowanych przez superformułę, który wygasł z dniem 10.05.2020.

We współrzędnych biegunowych , z promieniem i $\ displaystyle$ , superformuła to: $r}$

{\ Displaystyle r \ lewo (\ varphi \ prawej) = \ lewo (\ lewo | {\ Frac {\ cos \ lewo ({\ Frac {m \ varphi }{4}} \ prawej)}}} {a}} \ prawo |^{n_{2}}+\left|{\frac {\sin \left({\frac {m\varphi}}{4}}\right)}{b}}\right|^{n_{3} }\right)^{-{\frac {1}{n_{1}}}}.}

Wybierając różne wartości parametrów za ${\ Displaystyle a, b, m, n_ {1}, n_ {2},}$ n $\ Displaystyle n_ {3} ,}$ można wygenerować różne kształty.

Formuła została uzyskana przez uogólnienie superelipsy, nazwanej i spopularyzowanej przez duńskiego matematyka Pieta Heina .

Działki 2D

W poniższych przykładach wartości pokazane nad każdą cyfrą powinny wynosić m , n ₁ , n ₂ i n ₃ .

Program GNU Octave do generowania tych liczb

 
    0  
                   funkcja  sf2d  (  n, a  )  u  =  [  :  0,001  :  2  *  pi  ];  raux  =  abs  (  1  /  za  (  1  )  .*  abs  (  cos  (  n  (  1  )  *  u  /  4  )))  .^  n  (  3  )  +  abs  (  1  /  za  (         
         
      
       2  )  .*  abs  (  sin  (  n  (  1  )  *  u  /  4  )))  .^  n  (  4  );  r  =  abs  (  raux  )  .^  (  -  1  /  n  (  2  ));  x  =  r  .*  cos  (  u  );  y  =  r  .*  grzech  (  u 
   
 );  działka  (  x  ,  y  );  koniec

Rozszerzenie do wyższych wymiarów

Możliwe jest rozszerzenie formuły do 3, 4 lub n wymiarów za pomocą iloczynu sferycznego nadformuł. Na przykład powierzchnię parametryczną 3D uzyskuje się przez pomnożenie dwóch nadformuł r ₁ i r ₂ . Współrzędne są określone przez zależności:

{\ Displaystyle x = r_ {1} (\ teta) \ cos \ teta \ cdot r_ {2} (\ phi) \ cos \ phi }

{\ Displaystyle y = r_ {1} (\ teta) \ sin \ teta \ cdot r_ {2} (\ phi) \cos \phi ,}

{\ Displaystyle z = r_ {2} (\ phi) \ sin \ phi,}

gdzie ${\ Displaystyle \ phi}$ ( szerokość geograficzna ) waha się między - π / 2 a π / 2 i θ ( długość geograficzna ) między - π a π .

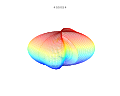
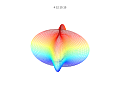
Działki 3D

Nadformuła 3D: a = b = 1; m , n ₁ , n ₂ i n ₃ są pokazane na rysunkach.

Program GNU Octave do generowania tych liczb:

 
     
         
    
    
     
       funkcja  sf3d  (  n, a  )  u  =  [  -  pi  :  0,05  :  pi  ];  v  =  [  -  pi  /  2  :  0,05  :  pi  /  2  ];  nu  =  długość  (  u  );  nv  =  długość  (  v  );  dla  i  =  1  :  nu  dla  j  =  
                         1  :  nv  raux1  =  abs  (  1  /  za  (  1  )  *  abs  (  cos  (  n  (  1  )  .*  u  (  ja  )  /  4  )))  .^  n  (  3  )  +  abs  (  1  /  a  (  2  )  *  abs  (  grzech  (  n  (  1       
             
               )  *  u  (  ja  )  /  4  )))  .^  n  (  4  );  r1  =  abs  (  raux1  )  .^  (  -  1  /  n  (  2  ));  raux2  =  abs  (  1  /  a  (  1  )  *  abs  (  cos  (  n  (  1  )  *  v  (  j                 
              )  /  4  )))  .^  n  (  3  )  +  abs  (  1  /  za  (  2  )  *  abs  (  sin  (  n  (  1  )  *  v  (  j  )  /  4  )))  .^  n  (  4  );  r2  =  abs  (  raux2  )  .^  (  -  1  /  rz 
               
               
       (  2  ));  x  (  ja  ,  jot  )  =  r1  *  sałata  (  u  (  ja  ))  *  r2  *  sałata  (  v  (  jo  ));  y  (  ja  ,  jot  )  =  r1  *  grzech  (  u  (  ja  ))  *  r2  *  sałata  (  v  (  jot  ));  z      
    
  
    
 (  ja  ,  jot  )  =  r2  *  grzech  (  v  (  jot  ));  koniec dla  ;  koniec dla  ;  siatka  (  x  ,  y  ,  z  );  funkcja końcowa  ;

Uogólnienie

Superformułę można uogólnić, dopuszczając różne m parametrów w dwóch wyrazach superformuły. Zastępując pierwszy parametr przez $displaystyle$ i drugi parametr przez z : $m$ }

{\ Displaystyle r \ lewo (\ varphi \ prawo) = \ lewo (\ lewo | {\ Frac {\ cos \ lewo ({\ Frac {y \ varphi} {4}} \ prawo)}} {a}} \ prawo |^{n_{2}}+\left|{\frac {\sin \left({\frac {z\varphi}}{4}}\right)}{b}}\right|^{n_{3} }\right)^{-{\frac {1}{n_{1}}}}}

Pozwala to na tworzenie struktur rotacyjnie asymetrycznych i zagnieżdżonych. W poniższych przykładach a, b, ${\ displaystyle {n_ {2}}}$ i ${\ displaystyle {n_ {3}}}$ wynoszą 1:

Linki zewnętrzne