Teoria hazardu i informacji

Wnioskowanie statystyczne można traktować jako teorię hazardu stosowaną do otaczającego nas świata. Niezliczone zastosowania logarytmicznych miar informacyjnych mówią nam dokładnie, jak najlepiej zgadywać w obliczu częściowych informacji. W tym sensie teorię informacji można uznać za formalne wyrażenie teorii hazardu. Nic więc dziwnego, że teoria informacji ma zastosowanie w grach losowych.

Zakłady Kelly'ego

Zakłady Kelly'ego lub zakłady proporcjonalne to zastosowanie teorii informacji do inwestowania i hazardu . Jej odkrywcą był John Larry Kelly Jr.

Częścią spostrzeżeń Kelly'ego było to, aby gracz maksymalizował oczekiwany logarytm swojego kapitału, a nie oczekiwany zysk z każdego zakładu. Jest to ważne, ponieważ w tym drugim przypadku ktoś byłby skłonny postawić wszystko, co miał, gdy zostałby przedstawiony korzystny zakład, a gdyby przegrał, nie miałby kapitału, z którym mógłby obstawiać kolejne zakłady. Kelly zdał sobie sprawę, że to logarytm kapitału gracza jest sumą w kolejnych zakładach i „do którego stosuje się prawo wielkich liczb”.

Informacje poboczne

Bit to wielkość entropii w obstawianym wydarzeniu z dwoma możliwymi wynikami i parzystymi szansami . Oczywiście moglibyśmy podwoić nasze pieniądze, gdybyśmy z góry wiedzieli, jaki będzie wynik tego wydarzenia. Kelly spostrzegł, że bez względu na to, jak skomplikowany jest scenariusz obstawiania, możemy zastosować optymalną strategię obstawiania, zwaną kryterium Kelly'ego , aby nasze pieniądze rosły wykładniczo, niezależnie od informacji pobocznych, które jesteśmy w stanie uzyskać. Wartość tych „nielegalnych” informacji dodatkowych jest mierzona jako wzajemne informacje odnoszące się do wyniku zdarzenia, które można obstawić:

{\ Displaystyle {\ rozpocząć {wyrównane} I (X; Y) & = \ mathbb {E} _ {Y} \ {D _ {\ operatorname {KL}}} {\ duży (} P (X | Y)\|P(X|I){\big )}\}\\&=\mathbb {E} _{Y}\{D_{\mathrm {KL}}}{\big (}P(X|{ \textrm {strona}}\ {\textrm {informacje}}\ Y)\|P(X|{\textrm {podane}}\ {\textrm {szanse}}\ I){\big )}\},\ koniec {wyrównany}}}

gdzie Y to informacja dodatkowa, X to wynik zdarzenia, w którym można postawić zakład, a I to stan wiedzy bukmachera. Jest to średnia dywergencja Kullbacka-Leiblera lub przyrost informacji rozkładu prawdopodobieństwa a posteriori X przy danej wartości Y w stosunku do rozkładu a priori lub określonych szans na X . Zauważ, że oczekiwanie jest przejęte przez Y , a nie X zanim zaczniemy obstawiać prawdziwe pieniądze na X , musimy ocenić, jak dokładne w dłuższej perspektywie są nasze informacje poboczne Y . Jest to proste zastosowanie wnioskowania bayesowskiego . Zauważ, że informacja dodatkowa Y może mieć wpływ nie tylko na naszą wiedzę o zdarzeniu X , ale także na samo zdarzenie. Na przykład Y może być koń, który miał za dużo owsa lub za mało wody. W tym przypadku obowiązuje ta sama matematyka, ponieważ z punktu widzenia bukmachera sporadyczne ustawianie wyścigów jest już brane pod uwagę przy ustalaniu kursów.

Charakter informacji pobocznych jest niezwykle wybredny. Widzieliśmy już, że może to wpłynąć na rzeczywiste zdarzenie, jak również na naszą wiedzę o wyniku. Załóżmy, że mamy informatora, który mówi nam, że wygra pewien koń. Z pewnością nie chcemy stawiać wszystkich naszych pieniędzy na tego konia tylko na podstawie plotki: ten informator może obstawiać innego konia i może rozpowszechniać plotki tylko po to, by sam uzyskać lepsze szanse. Zamiast tego, jak wskazaliśmy, musimy ocenić nasze informacje poboczne w dłuższej perspektywie, aby zobaczyć, jak korelują one z wynikami wyścigów. W ten sposób możemy dokładnie określić, jak rzetelny jest nasz informator i obstawiać precyzyjnie, aby zmaksymalizować oczekiwany logarytm naszego kapitału według kryterium Kelly'ego. Nawet jeśli nasz informator nas okłamuje, nadal możemy skorzystać z jego kłamstw, jeśli uda nam się znaleźć odwrotną korelację między jego typami a rzeczywistymi wynikami wyścigu.

Podwojenie stawki

Podwojenie stawki w grach hazardowych na wyścigach konnych jest

{\ Displaystyle W (b, p) = \ mathbb {E} [\ log _{2}S(X)]=\suma _{i=1}^{m}p_{i}\log _{2}b_{i}o_{i}}

gdzie są $i$ , prawdopodobieństwo wygranej tego $b_ {i}}$ wynosi , proporcja zakładu bogactwa na konia jest $}$ $\ displaystyle$ $}$ , a szanse (wypłata) wynoszą ${\ displaystyle o_ {i}}$ (np. ${\ displaystyle o_ {i} = 2},$ jeśli ja $\ displaystyle i}$ wygrany koń wypłaca podwójną kwotę zakładu). Ta ilość jest maksymalizowana przez hazard proporcjonalny (Kelly):

{\ displaystyle b = p \,}

dla którego

{\ Displaystyle \ max _ {b} W (b, p) = \ suma _ {i} p_ {i} \ log _{2}o_{i}-H(p)\,}

gdzie ${\ Displaystyle H (p)}$ to entropia informacji .

Oczekiwane zyski

Istnieje ważna, ale prosta zależność między ilością dodatkowych informacji, jakie otrzymuje gracz, a oczekiwanym wykładniczym wzrostem jego kapitału (Kelly):

{\ Displaystyle \ mathbb {E} \ log K_ {t} = \ log K_ {0} + \ suma _ {i = 1} ^ {t }Cześć}}

$i} }$ optymalnej strategii obstawiania, gdzie $jest$ kapitałem początkowym, jest kapitałem po t- tym zakładzie i $K.$ to ilość uzyskanych informacji pobocznych dotyczących i- tego zakładu (w szczególności informacji wzajemnych w stosunku do wyniku każdego możliwego do pokonania wydarzenia). To równanie ma zastosowanie w przypadku braku jakichkolwiek kosztów transakcyjnych lub minimalnych zakładów. Kiedy te ograniczenia mają zastosowanie (jak niezmiennie mają miejsce w prawdziwym życiu), w grę wchodzi kolejna ważna koncepcja hazardu: gracz (lub pozbawiony skrupułów inwestor) musi stawić czoła pewnemu prawdopodobieństwu ostatecznej ruiny, co jest znane jako scenariusz ruiny hazardzisty . Zauważ, że nawet jedzenie, odzież i schronienie można uznać za stałe koszty transakcyjne, a tym samym przyczynić się do prawdopodobieństwa ostatecznej ruiny gracza.

To równanie było pierwszym zastosowaniem teorii informacji Shannona poza dominującym paradygmatem komunikacji danych (Pierce).

Wnioski o samoinformację

Zaskoczenie i dowody w bitach, odpowiednio jako logarytmiczne miary prawdopodobieństwa i prawdopodobieństwa.

Logarytmiczna miara prawdopodobieństwa samoinformacji lub zaskoczenia, której średnią jest entropia /niepewność informacji i której średnią różnicą jest dywergencja KL , sama w sobie ma zastosowanie w analizie prawdopodobieństwa. Jego dwie główne mocne strony polegają na tym, że zaskakuje: (i) redukuje maleńkie prawdopodobieństwa do liczb o możliwej do opanowania wielkości oraz (ii) dodaje się, gdy prawdopodobieństwa się mnożą.

Na przykład można powiedzieć, że „liczba stanów równa się dwa liczbie bitów”, tj. #states = 2 ^#bits . Tutaj wielkość mierzona w bitach jest logarytmiczną miarą informacji wspomnianą powyżej. Dlatego jest N kawałków niespodzianki w wyrzuceniu wszystkich orłów w pierwszym rzucie N monet.

Addytywny charakter niespodzianek i umiejętność wyczucia ich znaczenia za pomocą garści monet może pomóc umieścić nieprawdopodobne zdarzenia (takie jak wygrana na loterii lub wypadek) w odpowiednim kontekście. Na przykład, jeśli jeden z 17 milionów losów jest zwycięzcą, to niespodzianka wygranej z pojedynczego losowania wynosi około 24 bitów. Rzucenie 24 monetami kilka razy może dać ci poczucie zaskoczenia, jakim jest zdobycie wszystkich orłów za pierwszym podejściem.

Addytywny charakter tego środka jest również przydatny przy ważeniu alternatyw. Na przykład wyobraź sobie, że zaskoczenie szkodliwości szczepionki wynosi 20 bitów. Jeśli zaskoczenie wywołane złapaniem choroby bez szczepionki wynosi 16 bitów, ale zaskoczenie szkodą spowodowaną chorobą, jeśli się ją złapie, wynosi 2 bity, to zaskoczenie krzywdą wynikającą z NIE otrzymania szczepionki wynosi tylko 16+2=18 bitów. Bez względu na to, czy zdecydujesz się na szczepienie, czy nie (np. koszt pieniężny za to nie jest omawiany w tej dyskusji), możesz w ten sposób przynajmniej wziąć odpowiedzialność za decyzję świadomą faktu, że nieszczepienie się wiąże się z więcej niż trochę dodatkowego ryzyka.

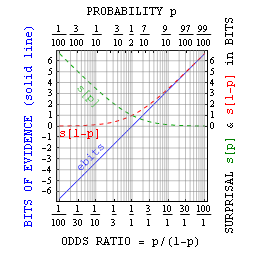
Mówiąc bardziej ogólnie, można powiązać prawdopodobieństwo p z bitami niespodziewanych bitów jako prawdopodobieństwo = 1/2 ^bitów . Jak zasugerowano powyżej, jest to przydatne głównie w przypadku małych prawdopodobieństw. Jednak Jaynes zwrócił uwagę, że przy twierdzeniach prawda-fałsz można również zdefiniować bity dowodów jako zaskoczenie przeciw minus zaskoczenie dla. Ten dowód w bitach odnosi się po prostu do ilorazu szans = p/(1-p) = 2 ^ebits i ma zalety podobne do zalet samej informacji o sobie.

Zastosowania w grach losowych

Teorię informacji można traktować jako sposób ilościowego określania informacji w celu podjęcia najlepszej decyzji w obliczu niedoskonałych informacji. To znaczy, jak podjąć najlepszą decyzję, korzystając tylko z dostępnych informacji. Celem obstawiania jest racjonalna ocena wszystkich istotnych zmiennych niepewnej gry/wyścigu/meczu, a następnie porównanie ich z ocenami bukmachera, które zazwyczaj mają postać kursów lub spreadów, i postawienie właściwego zakładu, jeśli oceny różnią się wystarczająco. Obszarem hazardu, w którym ma to największe zastosowanie, są zakłady sportowe. Upośledzenie sportowe bardzo dobrze nadaje się do teorii informacji ze względu na dostępność statystyk. Przez wiele lat znani ekonomiści testowali różne teorie matematyczne, używając sportu jako swojego laboratorium, z bardzo różnymi wynikami.

Jedna z teorii dotyczących zakładów sportowych głosi, że jest to błądzenie losowe . Spacer losowy to scenariusz, w którym nowe informacje, ceny i zwroty będą się wahać przypadkowo, jest to część hipotezy rynku efektywnego . U podstaw hipotezy efektywnego rynku leży przekonanie, że rynek zawsze będzie korygował wszelkie nowe informacje. Dlatego nikt nie może pokonać rynku, ponieważ handluje na tych samych informacjach, na podstawie których rynek się dostosował. Jednak według Famy, aby mieć efektywny rynek, muszą być spełnione trzy cechy:

Nie ma kosztów transakcyjnych w obrocie papierami wartościowymi
Wszystkie dostępne informacje są dostępne bezpłatnie dla wszystkich uczestników rynku
Wszyscy zgadzają się co do wpływu bieżących informacji na bieżącą cenę i rozkłady przyszłych cen każdego papieru wartościowego

Statystycy wykazali, że jest to trzeci warunek, który pozwala na przydatność teorii informacji w handicapach sportowych. Kiedy wszyscy nie są zgodni co do tego, jak informacje wpłyną na wynik wydarzenia, otrzymujemy różne opinie.

Zobacz też

Linki zewnętrzne