Kryterium Kelly'ego

Przykład optymalnego ułamka zakładów Kelly'ego w porównaniu z oczekiwanym zwrotem innych zakładów ułamkowych.

W teorii prawdopodobieństwa kryterium Kelly'ego (lub strategia Kelly'ego lub zakład Kelly'ego ) to wzór , który określa optymalną teoretyczną wielkość zakładu. Jest to ważne, gdy znane są oczekiwane zwroty. Wielkość zakładu Kelly'ego znajduje się poprzez maksymalizację oczekiwanej wartości logarytmu bogactwa, co jest równoważne z maksymalizacją oczekiwanej geometrycznej stopy wzrostu. JL Kelly Jr , naukowiec z Bell Labs , opisał to kryterium w 1956 roku. Ponieważ kryterium Kelly'ego prowadzi na dłuższą metę do większego bogactwa niż jakakolwiek inna strategia (tj. teoretyczny maksymalny zwrot, gdy liczba zakładów dąży do nieskończoności), jest to naukowa metoda hazardu.

Praktyczne zastosowanie formuły zostało zademonstrowane w grach hazardowych i ta sama idea została wykorzystana do wyjaśnienia dywersyfikacji w zarządzaniu inwestycjami . W 2000 roku analiza w stylu Kelly'ego stała się częścią głównego nurtu teorii inwestycji i twierdzono, że znani odnoszący sukcesy inwestorzy, w tym Warren Buffett i Bill Gross , używają metod Kelly'ego. Zobacz także Wybór portfela międzyokresowego .

Przykład optymalnego obstawiania

W jednym z badań każdy uczestnik otrzymał 25 dolarów i został poproszony o postawienie parzystych zakładów na monetę, która wypadnie orzeł w 60% przypadków. Uczestnicy mieli 30 minut na grę, więc mogli postawić około 300 zakładów, a pula nagród była ograniczona do 250 $. Ale zachowanie badanych było dalekie od optymalnego:

Co ciekawe, 28% uczestników zbankrutowało, a średnia wypłata wyniosła zaledwie 91 USD. Tylko 21% uczestników osiągnęło maksimum. 18 z 61 uczestników postawiło wszystko na jeden rzut, podczas gdy dwie trzecie postawiło na reszkę na pewnym etapie eksperymentu.

Stosując kryterium Kelly'ego i opierając się na prawdopodobieństwie w eksperymencie (pomijając górną granicę 250 $ i skończony czas trwania testu), właściwym podejściem byłoby postawienie 20% swojego bankrolla na każdy rzut monetą, co daje średni zysk 2,034% w każdej rundzie. To jest średnia geometryczna , a nie współczynnik arytmetyczny 4% ( ${\ Displaystyle r = (1 + 0,2 \ cdot 1,0) ^ {0,6} \ cdot (1-0,2 \ cdot 1,0) ^ {0,4}})$ . Teoretyczne oczekiwane bogactwo po 300 rundach wynosi 10 505 $ ( ${\ Displaystyle = 25 \ cdot (1,02034) ^ {300}}$ ), gdyby nie było ograniczone.

W tej konkretnej grze, ze względu na limit, strategia obstawiania tylko 12% puli na każdym rzucie przyniosłaby jeszcze lepsze wyniki (95% prawdopodobieństwo osiągnięcia limitu i średnia wypłata 242,03 $).

Formuła hazardu

Tam, gdzie przegranie zakładu wiąże się z utratą całego zakładu, zakład Kelly'ego wynosi:

{\ Displaystyle f ^ {*} = p - {\ Frac {q} {b}} = p - {\ Frac {1-p} {b}} }

Gdzie:

${\ displaystyle f ^ {*}}$ to ułamek obecnego bankrolla do postawienia.
${\ displaystyle p}$ to prawdopodobieństwo wygranej.
${\ displaystyle q}$ to prawdopodobieństwo straty ( ${\ displaystyle q = 1-p}$ ).
${\ displaystyle b}$ to proporcja zakładu wygranej. Np. Jeśli obstawiasz 10 $ na kursie 2 do 1 (po wygranej zwracasz 30 $, wygrywając 20 $), to ${\ Displaystyle b = \ 20 $ / \ 10 $ = 2,0}$ .

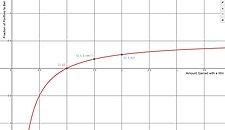Rysunek przedstawia na osi x kwotę uzyskaną dzięki wygranej w stosunku do ułamka portfela, który należy postawić na osi y. Liczba ta zakłada p=0,5 (że prawdopodobieństwo zarówno wygranej, jak i przegranej wynosi 50%). Jeśli kwota wygranej wynosi 1, kwota zakładu Kelly'ego wynosi 0 $, co ma sens w przypadku uczciwego zakładu bez oczekiwanego zysku.

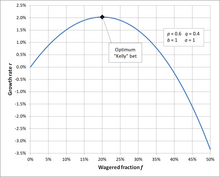
$0,4}$ jeśli hazard ma 60% szans na wygraną ( { $=$ ), a gracz otrzymuje szanse 1 do 1 $($ ( , a następnie, aby zmaksymalizować długoterminową stopę wzrostu bankrolla, gracz powinien obstawiać 20% bankrolla przy każdej ${\ textstyle f ^ {*} = 0,6- {\ frac {0,4} {1}} = 0,2}$ ).

Rysunek przedstawia na osi x kwotę uzyskaną dzięki wygranej w stosunku do ułamka portfela, który należy postawić na osi y. Liczba ta zakłada p=0,6 (że prawdopodobieństwo obu wygranych wynosi 60%).

Rysunek 3D przedstawiający optymalną wielkość zakładu Kelly'ego (oś pionowa) jako funkcję prawdopodobieństwa wygranej i kwoty wygranej.

Jeśli gracz ma zerową przewagę, tj. jeśli $kryterium$ , aby gracz nie stawiał

Jeśli przewaga jest ujemna ( $daje$ wynik ujemny, wskazując, że gracz powinien zająć drugą Na przykład w amerykańskiej ruletce obstawiającemu oferuje się równą wygraną ( ) na $czerwonym$ , gdy na kole jest 18 czerwonych liczb i 20 innych niż ${\ displaystyle p = 18/38}$ ). Zakład Kelly'ego to ${\ Displaystyle -1/19}$ , co oznacza, że gracz powinien postawić jedną dziewiętnastą swojego bankrolla, że czerwony nie pojawi się. W ruletce nie ma jednoznacznego przeciwko czerwonemu z porównywalnymi szansami, więc najlepsze, co gracz Kelly może zrobić, to nic nie postawić.

Formuła inwestycji

Bardziej ogólna postać formuły Kelly'ego dopuszcza częściowe straty, co jest istotne dla inwestycji:

{\ Displaystyle f ^ {*} = {\ Frac {p} {a}} - {\ Frac {q} {b}}}

Gdzie:

${\ displaystyle f ^ {*}}$ to ułamek aktywów, który należy zastosować do zabezpieczenia.
${\ displaystyle p}$ to prawdopodobieństwo, że wartość inwestycji wzrośnie.
${\ displaystyle q}$ to prawdopodobieństwo, że wartość inwestycji spadnie ( ${\ displaystyle q = 1-p}$ ).
${\ displaystyle a}$ to ułamek, który przegrywa w wyniku negatywnym. Jeśli cena papieru wartościowego spadnie o 10%, to ${\ displaystyle a = 0,1}$
${\ displaystyle b}$ to ułamek, który uzyskuje się w wyniku pozytywnym. Jeśli cena papieru wartościowego wzrośnie o 10%, to ${\ displaystyle b = 0,1}$ .

Należy zauważyć, że kryterium Kelly'ego jest ważne tylko dla znanych prawdopodobieństw wyniku, co nie ma miejsca w przypadku inwestycji. Inwestorzy niechętni do ryzyka nie powinni inwestować pełnej części Kelly'ego.

Ta formuła może skutkować ułamkami Kelly'ego wyższymi niż 1. W tym przypadku teoretycznie korzystne jest użycie dźwigni do zakupu dodatkowych papierów wartościowych na marży .

Dowód

Heurystyczne dowody kryterium Kelly'ego są proste. Kryterium Kelly'ego maksymalizuje oczekiwaną wartość logarytmu bogactwa (wartość oczekiwana funkcji jest sumą wszystkich możliwych wyników prawdopodobieństwa każdego konkretnego wyniku pomnożonego przez wartość funkcji w przypadku tego wyniku ). Zaczynamy od 1 jednostki bogactwa i stawiamy ułamek $bogactwa$ na wynik, który występuje z prawdopodobieństwem $displaystyle$ daje szanse równe $b}$ . Prawdopodobieństwo wygranej jest ${\ displaystyle p}$ iw takim przypadku powstałe bogactwo jest równe ${\ displaystyle 1 + fb}$ . Prawdopodobieństwo przegranej wynosi ${\ displaystyle q = 1-p}$ iw takim przypadku powstałe bogactwo jest równe ${\ displaystyle 1-fa}$ . Dlatego oczekiwana geometryczna stopa wzrostu wynosi: ${\ displaystyle r}$

\ Displaystyle R = (1 + fb) ^ {p} \ cdot (1-fa) ^ {q}}

Chcemy znaleźć maksymalne r tej krzywej (w funkcji f ), co wiąże się ze znalezieniem pochodnej równania. Łatwiej to osiągnąć, biorąc logarytm z każdej strony. Wynikowe równanie to:

{\ Displaystyle E = \ log (r) = p \ log (1 + fb) + q \ log (1-fa)}

gdzie oznacza $logarytmiczny$ bogactwa. Aby $znaleźć$ wartość, której tempo wzrostu jest zmaksymalizowane, oznaczoną jako , różniczkujemy powyższe wyrażenie i ustawiamy je $zero$ To daje:

{\ Displaystyle \ lewo. {\ Frac {dE} {df}} \ prawo | _ {f = f ^ {*} }={\frac {pb}{1+f^{*}b}}+{\frac {-qa}{1-f^{*}a}}=0}

Przekształcenie tego równania w celu rozwiązania dla wartości daje kryterium Kelly'ego: ${\ displaystyle f ^ {*}}$

{\ Displaystyle f ^ {*} = {\ Frac {p} {a}} - {\ Frac {q} {b}}}

$przegrana$ że to wyrażenie sprowadza się do prostej formuły hazardu, powoduje całkowitą utratę

Bernoulliego

W artykule z 1738 roku Daniel Bernoulli zasugerował, że mając do wyboru zakłady lub inwestycje, należy wybrać ten, który ma najwyższą średnią geometryczną wyników. Jest to matematycznie równoważne kryterium Kelly'ego, chociaż motywacja jest inna (Bernoulli chciał rozwiązać paradoks petersburski ).

Angielskie tłumaczenie artykułu Bernoulliego zostało opublikowane dopiero w 1954 roku, ale praca była dobrze znana wśród matematyków i ekonomistów .

Aplikacja na giełdę

W finansach matematycznych, jeśli wagi bezpieczeństwa maksymalizują oczekiwaną geometryczną stopę wzrostu (co jest równoważne z maksymalizacją bogactwa dziennika), to portfel jest optymalny dla wzrostu.

Obliczenia optymalnych portfeli wzrostu mogą napotkać ogromne problemy ze śmieciami. Na przykład w poniższych przypadkach przyjmuje się oczekiwaną stopę zwrotu i strukturę kowariancji aktywów, ale te parametry są w najlepszym przypadku szacunkami lub modelami obarczonymi znaczną niepewnością. Jeśli wagi portfeli są w dużej mierze funkcją błędów oszacowań, to ex post portfela optymalnego dla wzrostu mogą różnić się fantastycznie od przewidywań ex ante . Niepewność parametrów i błędy oszacowań to duży temat w teorii portfela. Podejściem do przeciwdziałania nieznanemu ryzyku jest inwestowanie mniej niż kryterium Kelly'ego (np. połowa).

Krytyka

Chociaż obietnica strategii Kelly'ego polegająca na osiąganiu lepszych wyników niż jakakolwiek inna strategia na dłuższą metę wydaje się przekonująca, niektórzy ekonomiści zaciekle argumentowali przeciwko niej, głównie dlatego, że specyficzne ograniczenia inwestycyjne danej osoby mogą przesłonić pragnienie optymalnej stopy wzrostu. Konwencjonalną alternatywą jest oczekiwanej użyteczności , która mówi, że wielkość zakładów powinna być tak dobrana, aby zmaksymalizować oczekiwaną użyteczność wyniku (dla osoby z logarytmem użyteczność, zakład Kelly'ego maksymalizuje oczekiwaną użyteczność, więc nie ma konfliktu; co więcej, oryginalna praca Kelly'ego wyraźnie stwierdza potrzebę funkcji użyteczności w przypadku gier hazardowych rozgrywanych skończenie wiele razy). Nawet zwolennicy Kelly'ego zwykle opowiadają się za ułamkowym Kelly'm (postawienie stałego ułamka kwoty zalecanej przez Kelly'ego) z różnych praktycznych powodów, takich jak chęć zmniejszenia zmienności lub ochrona przed niedeterministycznymi błędami w obliczeniach przewagi (przewagi).

Zaawansowana matematyka

Aby uzyskać rygorystyczny i ogólny dowód, zobacz oryginalny artykuł Kelly'ego lub niektóre inne odniesienia wymienione poniżej. Opublikowano kilka poprawek. Podajemy następujący nierygorystyczny argument dla przypadku z $pewnych$ zakład „parzyste pieniądze” 50:50), aby pokazać ogólny pomysł i dostarczyć Kiedy ${\ Displaystyle b = 1}$ , gracz Kelly stawia ${\ displaystyle 2p-1}$ razy ich początkowe bogactwo ${\ displaystyle W}$ , jak pokazane powyżej. $po$ wygrają, mają . Jeśli przegrają, mają ${\ Displaystyle 2 (1-p) W}$ . $Załóżmy,$ $razy$ takie zakłady i wygrywają $z$ tej serii . Powstałe bogactwo będzie:

{\ Displaystyle 2 ^ {N} p ^ {K} (1-p) ^ {NK} W \ !.}

Należy zauważyć, że uporządkowanie wygranych i przegranych nie wpływa na wynikowe bogactwo. $2p-1 + \$ $Displaystyle$ że inny gracz stawia inną kwotę, gdzie ${\ Displaystyle \ Delta}$ Delta może być dodatnia lub ujemna). Będą mieli ${\ Displaystyle (2p + \ Delta) W}$ po wygranej i ${\ Displaystyle [2 (1-p) - \ Delta] W}$ po przegranej. Po tej samej serii zwycięstw i porażek, co obstawiający Kelly, będą mieli:

{\ Displaystyle (2p + \ Delta) ^ {K} [2 (1-p) - \ Delta] ^ {NK} W}

Weź pochodną tego względem ${\ displaystyle \ Delta}$ i uzyskaj: Δ {\ displaystyle \ Delta}

{\ Displaystyle K (2p + \ Delta) ^ {K-1} [2 (1-p) - \ Delta] ^ {NK} W- (NK) (2p + \ Delta) ^ {K} [2 (1-p )-\Delta ]^{NK-1}W}

Funkcja jest maksymalizowana, gdy ta pochodna jest równa zeru, co występuje w:

{\ Displaystyle K [2 (1-p) - \ Delta] = (NK) (2p + \ Delta)}

co implikuje, że

{\ Displaystyle \ Delta = 2 \ lewo ({\ Frac {K} {N}} -p \ prawej)}

ale proporcja zwycięskich zakładów ostatecznie zbiegnie się do:

{\ Displaystyle \ lim _ {N \ do + \ infty} {\ Frac {K} {N}} = p}

według słabego prawa wielkich liczb . Tak więc na dłuższą metę ostateczne bogactwo jest maksymalizowane przez ustawienie $zero$ , co oznacza podążanie za strategią Kelly'ego. To pokazuje, że Kelly ma zarówno deterministyczny, jak i stochastyczny składnik. Jeśli ktoś zna K i N i chce obstawiać stałą część bogactwa za każdym razem (w przeciwnym razie mógłby oszukiwać i ^np . z największą ilością pieniędzy, jeśli ktoś obstawia:

{\ Displaystyle \ lewo (2 {\ Frac {K} {N}} -1 \ prawej) W}

za każdym razem. To prawda, czy $jest$ czy duży. $, ponieważ K nie$ $góry$ $staje$ , po prostu gdy się duży, zbliża . $,$ kto obstawia więcej niż Kelly, może zrobić lepiej, chwilę ktoś, kto stawia mniej niż Kelly, może wygrać lepiej, jeśli ${\ displaystyle K <pN}$ przez chwilę, ale na dłuższą metę Kelly zawsze wygrywa. Dowód heurystyczny dla przypadku ogólnego przebiega w następujący sposób. ^{[ potrzebne źródło ]} W pojedynczej próbie, jeśli zainwestujesz ułamek $swojego$ ${\ Displaystyle 1-f + f (1 + b) = 1 + fb}$ , jeśli twoja strategia się powiedzie, twój kapitał na koniec próby wzrośnie o współczynnik i podobnie, jeśli strategia się nie powiedzie, Twój kapitał zmniejszy się o czynnik ${\ Displaystyle 1-fa}$ . Tak więc na koniec $N$ (z $N$ i ) kapitał początkowy w wysokości 1 $ daje p $\ displaystyle$

{\ Displaystyle C_ {N} = (1 + fb) ^ {pN} (1-fa) ^ {qN}.}

Maksymalizacja $\ Displaystyle \ log (C_ {N}) / N}$ ${N}}$ , aw konsekwencji , w odniesieniu do prowadzi do pożądanego do ${\ Displaystyle$ wynik

{\ displaystyle f ^ {*} = p / aq / b.}

Edward O. Thorp przedstawił bardziej szczegółowe omówienie tego wzoru dla ogólnego przypadku. Można tam zauważyć, że podstawienie $sukcesów$ ” do liczby prób oznacza, że liczba prób musi być bardzo duża, ponieważ ${\ displaystyle p$ } zdefiniowany jako granica tego stosunku, gdy liczba prób dąży do nieskończoności. Krótko mówiąc, obstawianie za każdym razem prawdopodobnie zmaksymalizuje tempo wzrostu bogactwa tylko w przypadku, gdy liczba prób jest bardzo duża i fa $\ displaystyle f ^ {*}}$ ${\ displaystyle p}$ i ${\ displaystyle b}$ są takie same dla każdej próby. W praktyce jest to granie w kółko w tę samą grę, w której prawdopodobieństwo wygranej i szansa wypłaty są zawsze takie same. $niepowodzenia$ $powyższym$ heurystycznym dowodzie sukcesy i są wysoce prawdopodobne tylko $przypadku$

Wiele wyników

Kryterium Kelly'ego można uogólnić na hazard na wiele wzajemnie wykluczających się wyników, takich jak wyścigi konne. Załóżmy, że istnieje kilka wzajemnie wykluczających się wyników. Prawdopodobieństwo, że ${$ koń wygra wyścig, wynosi $\ displaystyle p_ {k}}$ , łączna kwota zakładów postawionych na $}$ koń wynosi ${\ displaystyle$ , i

{\ Displaystyle \ beta _ {k} = {\ Frac {B_ {k}}} {\ suma _ {i} B_ {i}}} = { \frac {D}{1+Q_{k}}},}

gdzie ${\ displaystyle Q_ {k}}$ to szanse wypłaty. ${\ Displaystyle D = 1-tt}$ , to stopa dywidendy, gdzie ${\ displaystyle tt}$ to przejęcie toru lub podatek, ${\ Displaystyle {\ Frac {D} {\ beta _ {k}}}} to stopa przychodów po odjęciu$ $przebicia$ toru, gdy koń wygrywa. Ułamek środków obstawiającego, na który można postawić ${\ displaystyle k}$ -ty koń to ${\ displaystyle f_ {k}}$ . Kryterium Kelly'ego dla hazardu z wieloma wzajemnie wykluczającymi się wynikami daje algorytm znajdowania optymalnego zestawu $postawić zakład$ i podaje wyraźny wzór na znalezienie optymalnych ${\ Displaystyle f_ {k} ^ {o}}$ bogactwa obstawiającego, aby postawić na wyniki zawarte w optymalnym zestawie ${\ Displaystyle S ^ {o}}$ . Algorytm optymalnego zestawu wyników składa się z czterech kroków:

Oblicz oczekiwaną stopę przychodu dla wszystkich możliwych (lub tylko kilku najbardziej obiecujących) wyników: ${\ Displaystyle er_ {i} = {\ Frac {DP_ {i}}} {\ beta _ {i}}} = p_ {i} ( Q_{i}+1)}$
$,$ aby nowa sekwencja była rosnąca. Zatem ${\ displaystyle er_ {1}}$ będzie najlepszym rozwiązaniem.
Zestaw ${\ Displaystyle S = \ varnothing}$ (pusty zestaw), ${\ Displaystyle k = 1}$ , ${\ Displaystyle R (S) = 1}$ . $_$ najlepszy _
Powtarzać:
Jeśli ${\ Displaystyle er_ {k} = {\ Frac {D} {\ beta _ {k}}} p_ {k}> R (S)} to$ wstaw ${\ Displaystyle k}$ -ty wynik do zestawu: ${\ Displaystyle S = S \ puchar \ {k \}}$ , przelicz zgodnie z ${\ Displaystyle R (S)}$ Formuła: ${\ Displaystyle R (S) = {\ Frac {D \ suma _ {k \ notin S} p_ {k}} {D- \sum _{k\w S}\beta _{k}}}}$
$k + 1}$ ${ \ Displaystyle$ , W przeciwnym razie ustaw i zatrzymaj

Jeśli optymalny zestaw $,$ to w ogóle nie obstawiaj. Jeśli zbiór optymalnych wyników nie jest pusty, to optymalny ułamek ${\ displaystyle k} -$ postawienia na $S$ $\ displaystyle S$ } wynik można obliczyć ze wzoru:

{\ Displaystyle f_ {i} = p_ {i} - \ beta _ {i} {\ Frac {\ suma _ {k \ notin S} p_ {k}} {\ lewo (D- \ suma _ {k \ in S}\beta _{k}\right)}}.}

Można to udowodnić

\ Displaystyle R (S ^ {o}) = 1 - \ suma _ {i \ w S ^ {o}} {f_ {i} ^ { o}}}

gdzie po prawej stronie jest stopa rezerwy ^{[ wymagane wyjaśnienie ]} . Dlatego mi $\ Displaystyle er_ {k} = {\ Frac {D} {\ beta _ {k}}} p_ {k}> R (S) }$ można interpretować w następujący sposób: ${\ displaystyle k}$ -ty wynik jest zawarty w zbiorze ${\ displaystyle S ^ {o}}$ optymalnych wyników wtedy i tylko wtedy, gdy oczekiwana stopa dochodu jest większa niż stopa rezerwy. Wzór na optymalny ułamek ${$ $displaystyle k$ jako nadwyżkę oczekiwanej stopy dochodów -tego konia nad stopą rezerwy podzieloną przez dochód k o po odjęciu toru weź, gdy $koń$ wygrywa lub jako przekroczenie prawdopodobieństwa ${\ displaystyle k}$ $odliczeniu$ toru, gdy -ty koń wygrywa. Binarny wykładnik wzrostu to

{\ Displaystyle G ^ {o} = \ suma _{i\in S}{p_{i}\log _{2}(er_{i})}+\left(1-\suma _{i\in S}{p_{i}}\right)\ log _{2}(R(S^{o})),}

a czas podwojenia wynosi

{\ Displaystyle T_ {d} = {\ Frac {1} {G ^ {o}}}.}

Ta metoda doboru optymalnych zakładów może być zastosowana również wtedy, gdy prawdopodobieństwa $są$ tylko dla kilku najbardziej obiecujących wyników, podczas gdy pozostałe wyniki nie mają szans na wygraną W tym przypadku tak musi być

{\ Displaystyle \ suma _ {i} {p_ {i} <1,} i

∑

\ Displaystyle \ suma _ {i} {\ beta _ {i}} <1}

.

Inwestycje giełdowe

Wielomian Taylora drugiego rzędu może służyć jako dobre przybliżenie głównego kryterium. Przede wszystkim jest to przydatne w przypadku inwestycji giełdowych, gdzie ułamek przeznaczony na inwestycję opiera się na prostych cechach, które można łatwo oszacować na podstawie istniejących danych historycznych – wartości oczekiwanej i wariancji . To przybliżenie prowadzi do wyników, które są solidne i dają wyniki podobne do pierwotnego kryterium.

W przypadku pojedynczych aktywów (akcji, funduszu indeksowego itp.) i stopy wolnej od ryzyka łatwo jest uzyskać optymalny ułamek do zainwestowania za pomocą geometrycznych ruchów Browna . Wartość zasobu o rozkładzie logarytmicznym $displaystyle$ czasie ( $wynosi$ S $S }$

{\ Displaystyle S_ {t} = S_ {0} \ exp \ lewo (\ lewo (\ mu - {\ Frac {\ sigma ^{2}}{2}}\right)t+\sigma W_{t}\right),}

z rozwiązania geometrycznego ruchu Browna, gdzie $procentowy$ ${\ Displaystyle W_ {t}}$ Wienera i $($ dryf ) i (procentowa zmienność) to stałe. Biorąc oczekiwania logarytmu:

{\ Displaystyle \ mathbb {E} \ log (S_ {t}) = \ log (S_ {0}) + \ lewo (\ mu - {\ Frac {\ sigma ^ {2}} {2}} \ prawo) T.}

Wtedy oczekiwany powrót dziennika wynosi R $\ displaystyle R_ {s}}$

{\ Displaystyle R_ {s} = \ lewo (\ mu - {\ Frac {\ sigma ^ {2}} {2}} \, \ prawo) s.}

Dla portfela składającego się z aktywów $S }$ obligacji płacących stopę wolną od ryzyka , z ułamkiem $}$ $\ displaystyle$ S ${\ displaystyle S$ i ${\ displaystyle (1-f)}$ w obligacji oczekiwany zwrot z jednego okresu jest określony przez

{\ Displaystyle \ mathbb {E} {\ lewo (f \ lewo [{\ Frac {S_ {1}} {S_ {0}}} -1 \ prawo] + (1-f) r \ prawo)} = \ mathbb {E} {\left(f\left[\exp \left(\left(\mu -{\frac {\sigma ^{2}}{2}}\right)+\sigma W_{1}\right )-1\prawo]\prawo)}+(1-f)r}

jednak wydaje się, że ludzie radzą sobie z oczekiwanym zwrotem dziennika dla jednego okresu zamiast w kontekście Kelly: sol ${\ displaystyle G (f)$

{\ Displaystyle G (f) = f \ mu - {\ Frac {(f \ sigma) ^ {2}} {2}} + ((1-f) \ r).}

Rozwiązując ${\ Displaystyle \ max (G (f))}$ otrzymujemy

{\ Displaystyle f ^ {*} = {\ Frac {\ mu -r} {\ sigma ^ {2}}}.}

${\ displaystyle f ^ {*}}$ to ułamek, który maksymalizuje oczekiwany zwrot logarytmiczny, a więc ułamek Kelly'ego. Thorp doszedł do tego samego wyniku, ale w inny sposób. $\ displaystyle R_ {s}}$ że różni się od powrotu z dziennika zasobów. $R$ . Mylenie tego jest częstym błędem popełnianym przez strony internetowe i artykuły mówiące o kryterium Kelly'ego.

$,$ wielu aktywów rozważmy rynek ze $r$ akcjami ze stochastycznymi zwrotami $displaystyle r_ {k}}$ $\ displaystyle k = 1, \ kropki, n,}$ k i wiązanie bez ryzyka ze zwrotem ${\ displaystyle r}$ . Inwestor wkłada $ułamek$ kapitału ${\ displaystyle S_ {k}},$ a reszta jest inwestowana w obligacje. Bez utraty ogólności załóżmy, że kapitał początkowy inwestora jest równy 1. Zgodnie z kryterium Kelly'ego należy maksymalizować

{\ Displaystyle \ mathbb {E} \ lewo [\ ln \ lewo ((1 + r) + \ sum \ limity _ {k = 1} ^ {n} u_ {k} (r_ {k} -r) \ prawo )\Prawidłowy].}

Rozszerzając to o szereg Taylora wokół ${\ Displaystyle {\ vec {u_ {0}}} = (0, \ ldots, 0)}$

{\ Displaystyle \ mathbb {E} \ lewo [\ ln (1 + r) + \ suma \ limity _ {k = 1} ^ {n} {\ Frac {u_ {k} (r_ {k} -r)} {1+r}}-{\frac {1}{2}}\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}u_{k}u_ {j}{\frac {(r_{k}-r)(r_{j}-r)}{(1+r)^{2}}}\right].}

W ten sposób redukujemy problem optymalizacji do programowania kwadratowego i rozwiązaniem nieograniczonym jest

{\ Displaystyle {\ vec {u ^ {\ gwiazda}}} = (1 + r) ({\ widehat {\ Sigma }})^{-1}({\widehat {\vec {r}}}-r)}

gdzie ${r}}}}$ $i$ są wektorem średnich i macierzą drugich mieszanych niecentralnych nadmiaru zwroty. Istnieje również algorytm numeryczny dla ułamkowych strategii Kelly'ego i dla optymalnego rozwiązania bez dźwigni finansowej i bez ograniczeń krótkiej sprzedaży.

Zobacz też

Linki zewnętrzne