Test rozcieńczenia

Termin test rozcieńczenia jest ogólnie używany do określenia specjalnego rodzaju testu biologicznego , w którym jeden lub więcej preparatów (np. lek) jest podawany jednostkom doświadczalnym w różnych poziomach dawek wywołujących mierzalną odpowiedź biologiczną. Poziomy dawek przygotowuje się przez rozcieńczenie w rozcieńczalniku, który jest obojętny pod względem odpowiedzi. Jednostkami doświadczalnymi mogą być na przykład kultury komórkowe, tkanki, narządy lub żywe zwierzęta. Odpowiedź biologiczna może być ilościowa (np. pozytywna/ujemna) lub ilościowa (np. wzrost). Celem jest powiązanie odpowiedzi z dawką, zwykle za pomocą interpolacji , aw wielu przypadkach wyrażenie mocy/aktywności badanego preparatu(-ów) w stosunku do wzorca znanej mocy/aktywności.

Testy rozcieńczeń mogą być bezpośrednie lub pośrednie. W teście bezpośredniego rozcieńczenia mierzy się ilość dawki potrzebną do wywołania specyficznej (ustalonej) odpowiedzi, tak że dawka jest zmienną stochastyczną określającą rozkład tolerancji . I odwrotnie, w teście pośredniego rozcieńczania poziomy dawek są podawane na ustalonych poziomach dawek, tak że odpowiedź jest zmienną stochastyczną.

Modele statystyczne

W celu matematycznej definicji testu rozcieńczenia przestrzeń obserwacyjna $zdefiniowana$ funkcja taka $,$ że odpowiedzi $}}$ są odwzorowywane na zbiór liczb rzeczywistych. $displaystyle$ funkcja , która wiąże dawkę z odpowiedzią { $F }$

{\ Displaystyle f (u) = F (z) + e}

w którym $,$ terminem błędu z oczekiwaniem 0. $się$ że jest ciągły i monotonny . W sytuacjach, w których zawarty jest preparat standardowy $S}$ zakłada się ponadto, że preparat testowy zachowuje się jak rozcieńczenie (lub stężenie) standardowego $displaystyle$

{\ Displaystyle F_ {T} (z) = F_ {S} (\ rho z)}

dla wszystkich

{\ Displaystyle z}

gdzie ${\ displaystyle \ rho > 0}$ jest względną siłą ${\ displaystyle T}$ . Jest to fundamentalne założenie podobieństwa krzywych dawka-odpowiedź, które jest niezbędne do sensownego i jednoznacznego zdefiniowania względnej siły działania. W wielu przypadkach wygodnie jest zastosować transformację potęgową $lub$ $0}$ $x=\log(z)$ transformację logarytmiczną ⁡ . Można wykazać, że ten ostatni przypadek $\lambda =0$ przypadkiem granicznym $\lambda \downarrow 0$ so if is written for the log transformation the above equation can be redefined as

{\ Displaystyle F_ {T} (x) = F_ {S} (\ rho ^ {\ lambda} x)}

dla wszystkich

{\ Displaystyle x}

.

Oszacowania są zwykle ograniczone do członków dobrze zdefiniowanej $przykład$ $się$ , na rodziny funkcji liniowych charakteryzujących wyrazem wolnym i a nachylenie. Techniki statystyczne, takie jak optymalizacja przez największe prawdopodobieństwo, mogą być wykorzystane do obliczenia oszacowań parametrów. Pod tym względem szczególne znaczenie ma teoria uogólnionych modeli liniowych , za pomocą których można modelować szeroki zakres testów rozcieńczania. Szacunki mogą opisywać $zadowalająco$ w zakresie testowanych dawek, ale niekoniecznie $opisywać$ poza $zakresem$ Nie oznacza to jednak, że odmienne krzywe można ograniczyć do przedziału, w którym są one podobne.

W praktyce $sobie$ rzadko jest interesujące. Bardziej interesujące jest oszacowanie $oszacowanie$ dawki, która wywołuje określoną odpowiedź. Szacunki te obejmują przyjmowanie stosunków statystycznie zależnych oszacowań parametrów. Twierdzenie Fiellera można wykorzystać do obliczenia przedziałów ufności tych stosunków.

Niektóre szczególne przypadki zasługują na szczególną uwagę ze względu na ich powszechne zastosowanie: jeśli $znane$ liniowy i $jako$ model współczynnika nachylenia . Jeśli $jest$ i jest $równoległej$ jako model linii . Innym powszechnie stosowanym modelem jest $dwumianowym$ probitowy $jest$ $w$ którym skumulowaną funkcją rozkładu normalnego , a zgodny z rozkładem .

Przykład: Test mikrobiologiczny antybiotyków

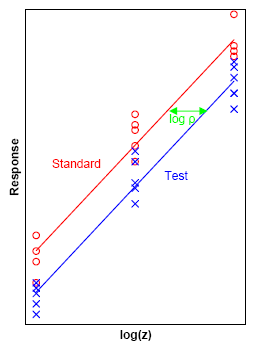
antybiotyku (pokazany na czerwono) i preparat testowy (pokazany na niebiesko) są nakładane w trzech poziomach dawek na wrażliwe mikroorganizmy na warstwie agaru na płytkach Petriego . Im silniejsza dawka, tym większa strefa zahamowania wzrostu mikroorganizmów. Odpowiedź biologiczna $odpowiedź$ $strefą$ zahamowania, a średnicę tej strefy można wykorzystać jako mierzalną Dawki $dwóch$ na logarytmy, najmniejszych kwadratów jest używana do dopasowania $.$ $) służy jako$ odległości w poziomie na zielono mocy ${\ Displaystyle \$ przygotowanie testu w stosunku do normy.

Oprogramowanie

Główne pakiety oprogramowania statystycznego nie obejmują testów rozcieńczeń, chociaż statystyk nie powinien mieć trudności z napisaniem odpowiednich skryptów lub makr w tym celu. Istnieje kilka pakietów oprogramowania specjalnego przeznaczenia do testów rozcieńczeń.

Finney, DJ (1971). Analiza probitowa, wyd. Cambridge University Press, Cambridge. ISBN 0-521-08041-X
Finney, DJ (1978). Metoda statystyczna w teście biologicznym, wyd. 3. Griffin, Londyn. ISBN 0-02-844640-2
Govindarajulu, Z. (2001). Statistical Techniques in Bioassay, wydanie drugie poprawione i rozszerzone, Karger, Nowy Jork. ISBN 3-8055-7119-4

Linki zewnętrzne

Oprogramowanie do testów rozcieńczeń: