Twierdzenie Pompejusza

Twierdzenie Pompeiu jest wynikiem geometrii płaskiej , odkrytej przez rumuńskiego matematyka Dimitrie Pompeiu . Twierdzenie jest proste, ale nie klasyczne. Stwierdza, co następuje:

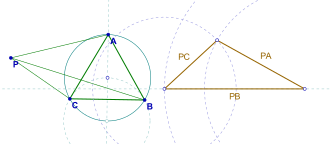
Biorąc pod uwagę trójkąt równoboczny ABC w płaszczyźnie i punkt P w płaszczyźnie trójkąta ABC, długości PA, PB i PC tworzą boki (być może zdegenerowanego) trójkąta.

Dowód twierdzenia Pompejusza z trójkątem Pompejusza ${\ displaystyle \ trójkąt PCP'}$

Dowód jest szybki. Rozważmy obrót o 60° wokół punktu B. Załóżmy, że A jest odwzorowane na C i P jest odwzorowane na P '. Następnie ${\ Displaystyle \ scriptstyle PB \ =\ P'B}$ i ${\ Displaystyle \ scriptstyle \ kąt PBP'\ = \ 60 ^ {\ circ}}$ . Stąd trójkąt PBP ' jest równoboczny, a ${\ Displaystyle \ scriptstyle PP'\ =\ PB}$ . Następnie ${\ displaystyle \ scriptstyle PA \ =\ P'C}$ . Zatem trójkąt PCP ' ma boki równe PA , PB i PC i dowód konstrukcji jest zakończony (patrz rysunek).

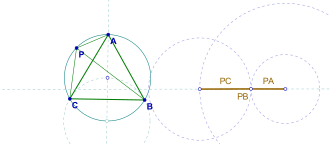
Dalsze badania ujawniają, że jeśli P nie znajduje się we wnętrzu trójkąta, ale raczej na okręgu opisanym , to PA , PB , PC tworzą zdegenerowany trójkąt, w którym największy jest równy sumie pozostałych. Obserwacja ta jest również znana jako Twierdzenie Van Schootena .

Ogólnie rzecz biorąc, na podstawie punktu P i długości wierzchołków trójkąta równobocznego - PA , PB i PC dwa trójkąty równoboczne (większy i mniejszy) o bokach za $\ displaystyle a_ {1}}$ i ${\ styl wyświetlania a_{2}}$ są zdefiniowane:

${\ Displaystyle {\ początek {wyrównane} a_ {1,2} ^{2}&={\frac {1}{2}}\left(PA^{2}+PB^{2}+PC^{2}\pm 4{\sqrt {3}}\triangle _{ (PA, PB, PC)}\right)\end{aligned}}}$ .

Symbol △ oznacza pole trójkąta, którego boki mają długości PA , PB , PC .

Pompejusz opublikował to twierdzenie w 1936 r., jednak August Ferdinand Möbius opublikował bardziej ogólne twierdzenie o czterech punktach na płaszczyźnie euklidesowej już w 1852 r. W tym artykule Möbius również wyraźnie wyprowadził stwierdzenie twierdzenia Pompejusza jako szczególny przypadek jego bardziej ogólnego twierdzenia. Z tego powodu twierdzenie to jest również znane jako twierdzenie Möbiusa-Pompeiu .

Linki zewnętrzne

• Strona MathWorld poświęcona twierdzeniu Pompejusza
• Twierdzenie Pompeiu na stronie cut-the-knot.org