Twierdzenie Siacciego

W kinematyce przyspieszenie cząstki poruszającej się po krzywej w przestrzeni jest pochodną jej prędkości po czasie . W większości zastosowań wektor przyspieszenia jest wyrażany jako suma składowych normalnych i stycznych , które są do siebie ortogonalne . Twierdzenie Siacciego, sformułowane przez włoskiego matematyka Francesco Siacciego (1839–1907), to kinematyczny rozkład wektora przyspieszenia na składowe promieniowe i styczne. Ogólnie komponenty promieniowe i styczne nie są do siebie prostopadłe. Twierdzenie Siacciego jest szczególnie przydatne w przypadku ruchów, w których moment pędu jest stały.

Twierdzenie Siacciego na płaszczyźnie

Ruch cząstki P w płaszczyźnie.

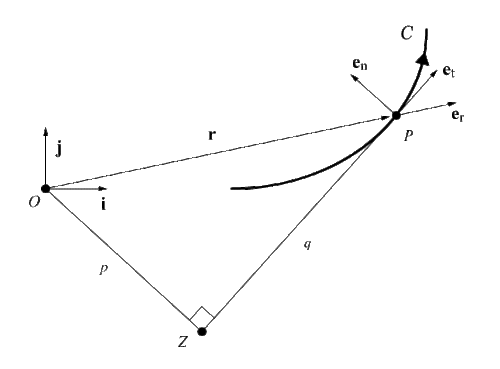
Niech cząstka P o masie m porusza się w dwuwymiarowej przestrzeni euklidesowej (ruch płaski). Załóżmy, że C jest krzywą wyznaczoną przez P , a s jest długością łuku C odpowiadającą czasowi t . Niech O będzie dowolnym początkiem płaszczyzny i { i , j } będzie ustaloną bazą ortonormalną . Wektor położenia cząstki to

{\ Displaystyle \ mathbf {r} = r \ mathbf {e} _ {r}.}

Wektor jednostkowy er _jest radialnym wektorem bazowym biegunowego układu współrzędnych na płaszczyźnie. Wektor prędkości cząstki to

{\ Displaystyle \ mathbf {v} = {\ Frac {d \ mathbf {r}} {dt}} = {\ kropka {s}} \ mathbf {e} _{t}=v\mathbf {e} _{t},}

gdzie e _t jest jednostkowym wektorem stycznym do C . Zdefiniuj moment pędu P jako

{\ Displaystyle \ mathbf {h} = \ mathbf {r} \ razy m \ mathbf {v} = h \ mathbf {k}}

gdzie k = ja x j . Załóżmy, że h ≠ 0 . Wektor pozycji r można zatem wyrazić jako

{\ Displaystyle \ mathbf {r} = q \ mathbf {e} _ {t} -p \ mathbf {e} _ {n}}

w układzie Serret-Frenet { e _t , en , e _b } _. Wielkość momentu pędu wynosi h = mpv , gdzie p jest prostopadłą od początku do stycznej ZP . Zgodnie z twierdzeniem Siacciego przyspieszenie a P można wyrazić jako

{\ Displaystyle \ mathbf {a} = - {\ Frac {\ kappa v ^ {2} r} {p}} \ mathbf {e} _ {r} + {\ Frac {(h ^ {2}) '} {2p^{2}}}\mathbf {e} _{t}=S_{r}\mathbf {e} _{r}+S_{t}\mathbf {e} _{t}.}

gdzie liczba pierwsza oznacza różniczkowanie względem długości łuku s , a κ jest funkcją krzywizny krzywej C . Ogólnie rzecz biorąc, nie _S r _i St są równe rzutom _ortogonalnym a na er i e _t .

Przykład: siły centralne

Załóżmy, że moment pędu cząstki P jest niezerową stałą i że S _r jest funkcją r . Następnie

{\ Displaystyle S_ {r} = - f (r) = - {\ Frac {\ kappa rh ^ {2}} { p^{3}}},\qquad S_{t}=0.}

Ponieważ krzywizna w punkcie orbity jest dana przez

{\ Displaystyle \ kappa = {\ Frac {1} {r}} {\ Frac {dp} {dr}},}

funkcję f można wygodnie zapisać jako ODE pierwszego rzędu

{\ Displaystyle f (r) = {\ Frac {h ^ {2}} {p ^ {3}}} {\ Frac {dp} {dr}}.}

Równanie zachowania energii dla cząstki otrzymuje się wtedy, gdy f ( r ) jest całkowalne.

{\ Displaystyle {\ Frac {1} {2}} {\ Frac {h ^ {2}} {p ^ {2}}} + \ int f (r) = \ operatorname {stała}.}

Twierdzenie Siacciego w przestrzeni

Twierdzenie Siacciego można rozszerzyć na ruchy trójwymiarowe. Zatem niech C będzie krzywą przestrzenną wyznaczoną przez P , a s to długość łuku C odpowiadająca czasowi t . Załóżmy również, że dwunormalna składowa momentu pędu nie znika. Wtedy wektor przyspieszenia P można wyrazić jako

{\ Displaystyle \ mathbf {a} = - {\ Frac {\ kappa v ^ {2} r} {p}} \ mathbf {e} _ {r} + \ lewo (v {\ Frac {dv} {ds} }+{\frac {\kappa v^{2}q}{p}}\right)\mathbf {e} _{t}.}

Składowa styczna jest styczna do krzywej C . Składowa promieniowa jest skierowana od punktu P do punktu, w którym prostopadła z dowolnego ustalonego początku styka się z płaszczyzną oscylacyjną . Inne wyrażenia na a można znaleźć w, gdzie podany jest nowy dowód twierdzenia Siacciego.

Zobacz też

F. Siacci. Moto per una linea plana. Atti della Reale Accademia della Scienze di Torino, XIV, 750–760, 1879.
F. Siacci. Moto per una linea gobba. Atti della Reale Accademia della Scienze di Torino, XIV, 946–951, 1879.
ET Whittaker . Traktat o dynamice analitycznej cząstek i ciał sztywnych . Wydanie 4, Cambridge University Press, Cambridge. Przedrukowane przez Dover Publications, Inc., Nowy Jork (1944).
Nathaniela Grossmana. Czysta radość mechaniki nieba. Birkäuser, Bazylea, 1996.