Twierdzenie Vincenta

W matematyce twierdzenie Vincenta - nazwane na cześć Alexandre'a Josepha Hidulphe'a Vincenta - jest twierdzeniem, które izoluje rzeczywiste pierwiastki wielomianów za pomocą współczynników wymiernych.

Chociaż twierdzenie Vincenta jest podstawą najszybszej metody izolowania pierwiastków rzeczywistych wielomianów, zostało prawie całkowicie zapomniane, przyćmione przez twierdzenie Sturma ; w związku z tym nie pojawia się w żadnej z klasycznych książek z teorii równań (z XX wieku), z wyjątkiem książki Uspienskiego . Przedstawiono dwa warianty tego twierdzenia wraz z kilkoma (ułamki ciągłe i bisekcja) wyprowadzonymi z nich metodami izolowania pierwiastków rzeczywistych.

Odmiana znaku

₀ Niech c , c ₁ , c ₂ , ... będzie skończonym lub nieskończonym ciągiem liczb rzeczywistych. Załóżmy, że l < r i spełnione są następujące warunki:

1. Jeśli r = l +1, to liczby c _l i c _r mają przeciwne znaki.
2. Jeśli r ≥ l +2, wszystkie liczby c _{l +1} , ..., c _{r −1} są równe zero, a liczby c _l i c _r mają przeciwne znaki.

Nazywa się to odmianą znaku lub zmianą znaku między liczbami c _l i c _r .

Gdy mamy do czynienia z wielomianem p ( x ) w jednej zmiennej, liczbę zmian znaku p ( x ) definiujemy jako liczbę zmian znaku w ciągu jego współczynników.

Przedstawiono dwie wersje tego twierdzenia: wersję ułamkową ciągłą ze względu na Vincenta oraz wersję bisekcji ze względu na Alesinę i Galuzziego.

Twierdzenie Vincenta: wersja ułamków ciągłych (1834 i 1836)

Jeżeli w równaniu wielomianowym o współczynnikach wymiernych i bez pierwiastków wielokrotnych dokonuje się kolejnych przekształceń postaci

${\ Displaystyle x = a_ {1} + {\ Frac {1} {x'} },\quad x'=a_{2}+{\frac {1}{x''}},\quad x''=a_{3}+{\frac {1}{x'''}}, \ldotki }$

gdzie za ${\ Displaystyle a_ {1}, a_ {2}, a_ {3}, \ ldots}$ dowolnymi liczbami dodatnimi większymi lub równymi jeden, to po pewnej liczbie takich przekształceń , otrzymane przekształcone równanie ma zmienność znaku zerowego lub zmianę pojedynczego znaku . W pierwszym przypadku nie ma pierwiastka, podczas gdy w drugim jest jeden dodatni pierwiastek rzeczywisty. Ponadto odpowiedni pierwiastek proponowanego równania jest przybliżony skończonym ułamkiem ciągłym:

${\ Displaystyle a_ {1} + {\ cfrac {1} {a_ {2} + {\ cfrac {1} {a_ {3} + {\ cfrac {1 }{\ddots }}}}}}}$

$,$ nieskończenie wiele liczb tę właściwość, to (nieskończony) odpowiedni ułamek ciągły.

Powyższe stwierdzenie jest dokładnym tłumaczeniem twierdzenia znalezionego w oryginalnych pracach Vincenta; jednak dla lepszego zrozumienia potrzebne są następujące uwagi:

• Jeśli $n podstawieniach (i$ wielomian uzyskany po mianownika), to istnieje N , że dla wszystkich $geq N }$ n albo $znaku lub$ . W tym drugim przypadku ${\ Displaystyle f_ {n} (x)}$ ma jeden dodatni pierwiastek rzeczywisty dla wszystkich ${\ displaystyle n \ geq N}$ .
• Ułamek ciągły reprezentuje dodatni pierwiastek pierwotnego równania, a oryginalne równanie może mieć więcej niż jeden pierwiastek dodatni. Co więcej, zakładając , możemy uzyskać tylko pierwiastek z pierwotnego równania, który wynosi > 1. Aby uzyskać dowolny dodatni pierwiastek, musimy założyć, że $geq$$1} styl wyświetlania a_{1}\geq 0}$ .
• Pierwiastki ujemne uzyskuje się przez zastąpienie x przez − x , w którym to przypadku pierwiastki ujemne stają się dodatnie.

Twierdzenie Vincenta: wersja bisekcji (Alesina i Galuzzi 2000)

Niech p ( x ) będzie wielomianem rzeczywistym stopnia deg ( p ), który ma tylko pierwiastki proste. Można wyznaczyć taką wielkość dodatnią δ, że dla każdej pary dodatnich liczb rzeczywistych a , b z ${\ Displaystyle | ba | <\ delta}$ , każdy przekształcony wielomian postaci

${\ Displaystyle f (x) = (1 + x) ^ {\ stopień (p)} p \ lewo ( {\frac {a+bx}{1+x}}\right)}$

 

 

 

 

()

ma dokładnie 0 lub 1 odmianę znaku . Drugi przypadek jest możliwy wtedy i tylko wtedy, gdy p ( x ) ma pojedynczy pierwiastek w obrębie ( a , b ).

„Test korzeni a_b” Alesiny – Galuzziego

Z równania ( 1 ) otrzymujemy następujące kryterium określające, czy wielomian ma pierwiastki w przedziale ( a , b ):

Wykonaj na p ( x ) podstawienie

${\ Displaystyle x \ strzałka w lewo {\ Frac {a + bx} {1 + x}}}$

i policz liczbę zmian znaku w ciągu współczynników przekształconego wielomianu; ta liczba daje górną granicę liczby pierwiastków rzeczywistych p ( x ) w przedziale otwartym ( a , b ). Dokładniej, liczba ρ _ab ( p ) pierwiastków rzeczywistych w przedziale otwartym ( a , b ) — zliczone krotności — wielomianu p ( x ) w R [ x ], stopnia deg( p ), jest ograniczona powyżej liczbą zmian znaku var _ab ( p ), gdzie

${\ Displaystyle \ nazwa operatora {var} _ {ab} (p) =$

${\ Displaystyle \ nazwa operatora {var} _ {ab} (p) = \ nazwa operatora {var} _ {ba} (p) \ geq \ rho _ {ab} (p).}$

Podobnie jak w przypadku reguły znaków Kartezjusza, jeśli var _ab ( p ) = 0, to ρ _ab ( p ) = 0, a jeśli var _ab ( p ) = 1, to ρ _ab ( p ) = 1.

Szczególnym przypadkiem „testu korzeni a_b” Alesiny – Galuzziego jest „test korzeni 0_1” Budana .

Szkic dowodu

Szczegółowe omówienie twierdzenia Vincenta, jego rozszerzenia, geometrycznej interpretacji zachodzących przekształceń oraz trzech różnych dowodów można znaleźć w pracy Alesiny i Galuzziego. Czwarty dowód pochodzi od Ostrowskiego , który ponownie odkrył szczególny przypadek twierdzenia podanego przez Obreschkoffa , s. 81, w latach 1920–1923.

Aby udowodnić (obie wersje) twierdzenia Vincenta, Alesina i Galuzzi pokazują, że po serii przekształceń wymienionych w twierdzeniu, wielomian z jednym pierwiastkiem dodatnim ostatecznie ma jedną odmianę znaku. Aby to pokazać, używają następującego wniosku do wspomnianego wcześniej twierdzenia Obreschkoffa z lat 1920–1923; to znaczy następujący wniosek podaje warunki konieczne, w których wielomian z jednym dodatnim pierwiastkiem ma dokładnie jedną zmianę znaku w sekwencji swoich współczynników; patrz także odpowiedni rysunek.

Następstwo. ( Twierdzenie o stożku lub sektorze Obreschkoffa , 1920–1923 s. 81): Jeśli prawdziwy wielomian ma jeden pierwiastek prosty x ₀ , a wszystkie inne (prawdopodobnie wielokrotne) pierwiastki leżą w sektorze

${\ Displaystyle S _ {\ sqrt {3}} = \ lewo \ {x = - \ alfa + i \ beta \: \ | \ beta | \ równoważnik {\ sqrt {3}} | \ alfa |, \alpha >0\prawo\}}$

wtedy sekwencja jego współczynników ma dokładnie jedną zmianę znaku.

S ${\ Displaystyle S _ {\ sqrt {3}}}$ Obreschkoffa i jego słynna figura w kształcie ósemki (okręgów)

Rozważmy teraz transformację Möbiusa

${\ Displaystyle M (x) = {\ Frac {ax + b} {cx + d}} \ qquad za ,b,c,d\w \mathbb {Z} _{>0}}$

oraz trzy okręgi pokazane na odpowiednim rysunku; załóżmy, że   a / c < b / d .

• (Żółte) kółko

${\ Displaystyle \ lewo | x - {\ tfrac {1} {2}} \ lewo ({\ tfrac {a} {c}} + {\ tfrac {b} {d} }}\right)\right|={\tfrac {1}{2}}\left({\tfrac {b}{d}}-{\tfrac {a}{c}}\right)} którego średnica$

leży na osi rzeczywistej, z punktami końcowymi a / c i b / d ,

${\ Displaystyle M ^ {-1} (x) = {\ Frac {dx-b} {-cx + a$

re

na wyimaginowaną oś. Na przykład punkt

${\ Displaystyle {\ tfrac {1} {2}} \ lewo ({\ tfrac {a} {c}} + {\ tfrac {b} {d}} \ prawej) + {\ tfrac {i} {2} }\left({\tfrac {b}{d}}-{\tfrac {a}{c}}\right)} zostaje$

odwzorowane na punkt   − i d / c . Punkty zewnętrzne są mapowane na półpłaszczyznę z Re( x ) < 0 .

• Dwa okręgi (widoczne są tylko ich niebieskie półksiężyce) ze środkiem

${\ Displaystyle {\ tfrac {1} {2}} \ lewo ({\ tfrac {a} {c}} + {\ tfrac {b} {d}} \ prawej) \ pm {\ tfrac {i }{2{\sqrt {3}}}}\left({\tfrac {b}{d}}-{\tfrac {a}{c}}\right)} i$

promień

${\ Displaystyle {\ tfrac {1} {\ sqrt {3}}} \ lewo ({\ tfrac {b} {d}} - {\ tfrac {a} {c}} \ prawej)$

} odwrotna transformacja Möbiusa

${\ Displaystyle M ^ {- 1} (x) = {\ Frac {dx-b} {-cx + a}}}$

na linie Im ( x ) = ± √ 3 Re ( x ) . Na przykład punkt

$\ Displaystyle {\ tfrac {1} {2}} \ lewo ({\ tfrac {a} {c} }+{\tfrac {b}{d}}\right)-{\tfrac {3i}{2{\sqrt {3}}}}\left({\tfrac {b}{d}}-{\tfrac {a}{c}}\prawo)}$

zostaje odwzorowany na punkt

${\ Displaystyle {\ tfrac {-d} {2c}} \ lewo (1-i {\ sqrt {3}} \ prawej).} Punkty$

zewnętrzne (te poza figurą w kształcie ósemki) są mapowane na ${\ displaystyle S _ {\ sqrt {3}}}$ .

Z powyższego staje się oczywiste, że jeśli wielomian ma jeden dodatni pierwiastek wewnątrz ósemki, a wszystkie inne pierwiastki są poza nim, przedstawia zmianę jednego znaku w sekwencji jego współczynników. Gwarantuje to również zakończenie procesu.

Tło historyczne

Wczesne zastosowania twierdzenia Vincenta

W swoich fundamentalnych pracach Vincent przedstawił przykłady, które dokładnie pokazują, jak wykorzystać jego twierdzenie do wyodrębnienia pierwiastków rzeczywistych wielomianów z ułamkami ciągłymi . Jednak wynikowa metoda miała wykładniczy czas obliczeń, z czego matematycy musieli zdawać sobie wtedy sprawę, jak zdał sobie sprawę Uspienski p. 136, sto lat później.

Poszukiwanie pierwiastka przez Vincenta (z zastosowaniem twierdzenia Budana)

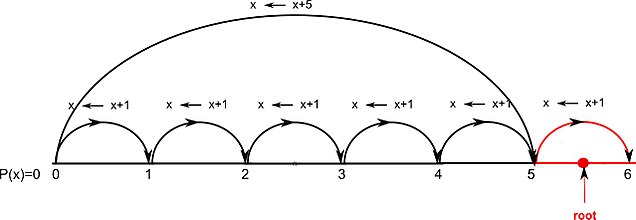
Wykładniczy charakter algorytmu ai _Vincenta wynika ze sposobu obliczania ilorazów cząstkowych (w twierdzeniu Vincenta ). To znaczy, aby obliczyć każdy iloraz częściowy ai _{jako „} (czyli zlokalizować pierwiastki na osi x ) Vincent używa twierdzenia Budana testu braku pierwiastków” ; innymi słowy, aby znaleźć część całkowitą pierwiastka Vincent wykonuje kolejne podstawienia postaci x ← x +1 i ustaje tylko wtedy, gdy wielomiany p ( x ) i p ( x +1) różnią się liczbą zmian znaku w ciągu ich współczynników (tj. gdy liczba zmian znaku p ( x +1 ) maleje) .

Zobacz odpowiedni diagram, gdzie pierwiastek leży w przedziale (5, 6). Można łatwo wywnioskować, że jeśli pierwiastek jest daleko od początku, znalezienie w ten sposób jego części całkowitej zajmuje dużo czasu, stąd wykładniczy charakter metody Vincenta. Poniżej znajduje się wyjaśnienie, w jaki sposób przezwyciężono tę wadę.

Zniknięcie twierdzenia Vincenta

Vincent był ostatnim autorem w XIX wieku, który użył swojego twierdzenia do wyodrębnienia pierwiastków rzeczywistych wielomianu.

Powodem tego było pojawienie się w 1827 r. twierdzenia Sturma , które rozwiązało problem izolacji pierwiastków rzeczywistych w czasie wielomianowym , określając dokładną liczbę pierwiastków rzeczywistych wielomianu w rzeczywistym przedziale otwartym ( a , b ). Powstała metoda (Sturma) obliczania pierwiastków rzeczywistych wielomianów była jedyną szeroko znaną i stosowaną od tamtej pory - do około 1980 roku, kiedy to została zastąpiona (w prawie wszystkich systemach algebry komputerowej) metodami wywodzącymi się z twierdzenia Vincenta , z których najszybszą jest metoda Vincenta–Akritasa–Strzebońskiego (VAS).

Serret zawarł w swojej Algebrze, s. 363–368, twierdzenie Vincenta wraz z jego dowodem i skierował wszystkich zainteresowanych czytelników do artykułów Vincenta, aby zapoznać się z przykładami jego użycia. Serret był ostatnim autorem, który wspomniał o twierdzeniu Vincenta w XIX wieku.

Powrót twierdzenia Vincenta

W XX wieku twierdzenia Vincenta nie można znaleźć w żadnym podręczniku teorii równań; jedynymi wyjątkami są książki Uspienskiego i Obreschkoffa , gdzie w drugiej jest tylko stwierdzenie twierdzenia.

To właśnie w książce Uspienskiego Akritas znalazł twierdzenie Vincenta i uczynił z niego temat swojego doktoratu. Thesis „Vincent's Theorem in Algebraic Manipulation”, North Carolina State University, USA , 1978. Głównym osiągnięciem w tamtym czasie było zdobycie oryginalnej pracy Vincenta z 1836 roku, coś, co umknęło Uspienskiemu — co doprowadziło do wielkiego nieporozumienia . Oryginalna praca Wincentego z 1836 roku została udostępniona Akritasowi dzięki godnym pochwały wysiłkom (wypożyczanie międzybiblioteczne) bibliotekarza w Bibliotece Uniwersytet Wisconsin-Madison, Stany Zjednoczone .

Metody izolacji pierwiastków rzeczywistych wyprowadzone z twierdzenia Vincenta

Wyodrębnianie pierwiastków rzeczywistych wielomianu to proces znajdowania otwartych przedziałów rozłącznych, z których każdy zawiera dokładnie jeden pierwiastek rzeczywisty, a każdy pierwiastek rzeczywisty mieści się w jakimś przedziale. Według francuskiej szkoły matematycznej XIX wieku jest to pierwszy krok w obliczaniu rzeczywistych pierwiastków, a drugim jest ich przybliżenie z dowolnym stopniem dokładności; ponadto nacisk kładziony jest na dodatnie , ponieważ aby wyodrębnić pierwiastki ujemne wielomianu p ( x ) zastąp x przez − x ( x ← − x ) i powtórz proces.

Wersję twierdzenia Vincenta o ułamkach ciągłych można wykorzystać do wyodrębnienia dodatnich pierwiastków danego wielomianu p ( x ) stopnia deg ( p ). Aby to zobaczyć, przedstaw transformację Möbiusa

${\ Displaystyle M (x) = {\ Frac {ax + b} {cx + d}}, \ qquad a, b,c,d\w \mathbb {N} }$

ułamek ciągły, który prowadzi do przekształconego wielomianu

${\ Displaystyle f (x) = (cx + d) ^ {\ stopień (p)} p \ lewo({\frac {ax+b}{cx+d}}\prawo)}$

 

 

 

 

()

z jedną zmianą znaku w sekwencji jego współczynników. Wtedy pojedynczy dodatni pierwiastek z f ( x ) (w przedziale (0, ∞)) odpowiada temu dodatniemu pierwiastkowi z p ( x ), który znajduje się w przedziale otwartym z punktami końcowymi ${\ displaystyle {\ frac {b} {d}}}$ i ${\ Displaystyle {\ Frac {a} {c}}}$ . Te punkty końcowe nie są uporządkowane i odpowiadają odpowiednio M (0) i M (∞).

Dlatego, aby wyizolować dodatnie pierwiastki wielomianu, wszystko, co należy zrobić, to obliczyć - dla każdego pierwiastka - zmienne a , b , c , d odpowiedniej transformacji Möbiusa

${\ Displaystyle M (x) = {\ Frac {ax + b} {cx + d}}}$

co prowadzi do przekształconego wielomianu jak w równaniu ( 2 ), z jedną zmianą znaku w sekwencji jego współczynników.

Kluczowa obserwacja: Zmienne a , b , c , d transformacji Möbiusa

${\ Displaystyle M (x) = {\ Frac {ax + b} {cx + d}}}$

(w twierdzeniu Vincenta ) prowadzący do przekształconego wielomianu — jak w równaniu ( 2 ) — przy jednym znaku zmiany ciągu jego współczynników można obliczyć:

• albo przez ułamki ciągłe , co prowadzi do metody ułamków ciągłych Vincenta – Akritasa – Strzebońskiego (VAS) ,
• lub przez bisekcję , prowadzącą (między innymi) do metody bisekcji Vincenta – Collinsa – Akritasa (VCA) .

„Część bisekcji” tej bardzo ważnej obserwacji pojawiła się jako specjalne twierdzenie w artykułach Alesiny i Galuzziego.

Wszystkie metody opisane poniżej (patrz artykuł na temat twierdzenia Budana, aby zapoznać się z ich tłem historycznym) muszą obliczyć (raz) górną granicę, ub , wartości dodatnich pierwiastków rozważanego wielomianu. Wyjątkiem jest VAS , gdzie dodatkowo dolne granice lb muszą być wyliczane niemal w każdym cyklu pętli głównej. Aby obliczyć dolną granicę lb wielomianu p ( x ) oblicz górną granicę ub wielomianu ${\ Displaystyle x ^ {\ stopień (p)} p \ lewo ({\ Frac {1} {x}} \ prawej)} i$ ustawić ${\ Displaystyle lb = {\frac {1}{ub}}}$ .

Doskonałe (górne i dolne) granice wartości samych pierwiastków dodatnich wielomianów zostały opracowane przez Akritasa, Strzebońskiego i Vigklasa na podstawie wcześniejszych prac Doru Stefanescu. Są one opisane w pracy doktorskiej PS Vigklasa. Praca dyplomowa i gdzie indziej. Granice te zostały już zaimplementowane w systemach algebry komputerowej Mathematica , SageMath , SymPy , Xcas itp.

Wszystkie trzy metody opisane poniżej są zgodne z doskonałą prezentacją François Boulier, s. 24.

Metoda ułamków ciągłych

Tylko jedna metoda ułamków ciągłych wywodzi się z twierdzenia Vincenta . Jak wspomniano powyżej , zaczęło się to w latach trzydziestych XIX wieku, kiedy Vincent przedstawił w artykułach kilka przykładów, które pokazują, jak wykorzystać jego twierdzenie do wyodrębnienia pierwiastków rzeczywistych wielomianów z ułamkami ciągłymi . Jednak wynikowa metoda miała wykładniczy czas obliczeniowy. Poniżej znajduje się wyjaśnienie ewolucji tej metody.

Vincent–Akritas–Strzeboński (VAS, 2005)

Jest to druga metoda (po VCA ) opracowana do obsługi wykładniczego zachowania metody Vincenta.

Metoda ułamków ciągłych VAS jest bezpośrednią implementacją twierdzenia Vincenta. Pierwotnie został przedstawiony przez Vincenta w latach 1834-1938 w artykułach w formie wykładniczej; mianowicie Vincent obliczył każdy iloraz częściowy + 1, które _ai przez szereg _równoważne przyrostów jednostek ai ← _ai są podstawieniom postaci x ← x + 1.

Metoda Vincenta została przekształcona w formę złożoności wielomianowej przez Akritasa, który w swoim doktoracie z 1978 r. Teza ( Twierdzenie Vincenta w manipulacji algebraicznej , North Carolina State University ai _, USA) obliczyła każdy iloraz częściowy jako dolną granicę, lb , wartości dodatnich pierwiastków wielomianu. Nazywa się to idealną dodatnią dolną granicą pierwiastka, która oblicza całkowitą część najmniejszego dodatniego pierwiastka (patrz odpowiedni rysunek). Mianowicie, ustaw teraz a _i ← lb lub równoważnie wykonaj podstawienie x ← x + lb , które zajmuje mniej więcej tyle samo czasu co podstawienie x ← x + 1.

VAS szuka pierwiastka: idealna dolna granica to 5, stąd x ← x + 5.

dodatnia $\ Displaystyle lb_ {obliczone}> 16}$ granica pierwiastka nie istnieje, Strzeboński wprowadził w 2005 roku podstawienie $\ Displaystyle x \ leftarrow lb_ {obliczony} * x$ ; ogólnie ${\ displaystyle lb> lb_ {obliczone}}$ a wartość 16 została określona eksperymentalnie. Ponadto wykazano, że metoda VAS ( ułamki ciągłe ) jest szybsza od najszybszej implementacji metody VCA (bisekcji), co zostało niezależnie potwierdzone; dokładniej, dla wielomianów Mignotte'a wysokiego stopnia VAS jest około 50 000 razy szybszy niż najszybsza implementacja VCA.

W 2007 roku Sharma usunął hipotezę idealnej dodatniej dolnej granicy i udowodnił, że VAS jest nadal wielomianem w czasie.

VAS jest domyślnym algorytmem izolacji roota w Mathematica , SageMath , SymPy , Xcas .

Aby porównać metodę Sturma i VAS, użyj funkcji realroot(poly) i time(realroot(poly)) Xcas . Domyślnie, aby wyizolować prawdziwe korzenie poly realroot, stosuje się metodę VAS; aby użyć metody Sturma, napisz realroot(sturm, poly). Zobacz także Linki zewnętrzne do aplikacji autorstwa A. Berkakisa na urządzenia z Androidem, która robi to samo.

Oto jak działa VAS( p , M ), gdzie dla uproszczenia nie uwzględniono wkładu Strzebońskiego:

• Niech p ( x ) będzie wielomianem stopnia deg ( p ) takim, że p (0) ≠ 0. Aby wyizolować jego dodatnie pierwiastki, skojarz z p ( x ) transformację Möbiusa M ( x ) = x i powtórz następujące kroki podczas są pary { p ( x ), M ( x )} do przetworzenia.
• Użyj reguły znaków Kartezjusza na p ( x ), aby obliczyć, jeśli to możliwe, (używając liczby var zmian znaku w sekwencji jego współczynników) liczbę jego pierwiastków w przedziale (0, ∞). Jeśli nie ma pierwiastków, zwróć zbiór pusty, ∅ natomiast jeśli pierwiastek jest jeden, zwróć przedział ( a , b ), gdzie a = min( M (0), M (∞)), a b = max ( M (0) ), M (∞)); jeśli b = ∞ zbiór b = ub , gdzie ub jest górną granicą wartości dodatnich pierwiastków p ( x ).
• Jeśli istnieją dwie lub więcej odmian znaków, reguła znaków Kartezjusza implikuje, że w przedziale (0, ∞) może być zero, jeden lub więcej rzeczywistych pierwiastków; w tym przypadku rozważ osobno pierwiastki z p ( x ), które leżą w przedziale (0, 1) od pierwiastków z przedziału (1, ∞). Należy przeprowadzić specjalny test dla 1.
  • Aby zagwarantować, że w przedziale (0, 1) idealnej dolnej granicy znajdują się pierwiastki, stosuje się lb ; $dodatniego$ pomocą dolnej wartościach p ( x ). Jeżeli $x$$\$ > podstawienie wykonywane p ( ) _ _ x ), podczas gdy ${\ Displaystyle lb_ {obliczony} \ równoważnik 1$ użyj podstawienia(ów) x ← x +1, aby znaleźć część całkowitą pierwiastka(ów).
  • Aby obliczyć pierwiastki w przedziale (0, 1), wykonaj podstawienie na p ( x ) i M ( x ) ${\ Displaystyle x \ leftarrow {\ Frac {1} {1 + x}}}$ i przetworzyć parę

${\ Displaystyle \ lewo \ {(1 + x) ^ {\ stopień (p)} p \ left({\tfrac {1}{1+x}}\right),M({\tfrac {1}{1+x}})\right\},} natomiast aby obliczyć pierwiastki z przedziału (1$

, ∞) wykonaj podstawienie x ← x + 1 na p ( x ) i M ( x ) i przetwarzamy parę { p (1 + x ), M (1 + x )}. Równie dobrze może się okazać, że 1 jest pierwiastkiem p ( x ), w którym to przypadku M (1) jest pierwiastkiem pierwotnego wielomianu, a przedział izolacji zmniejsza się do punktu.

Poniżej znajduje się rekurencyjna prezentacja VAS( p , M ).

VAS ( p , M ):

Dane wejściowe : jednowymiarowy wielomian bez kwadratów ${\ Displaystyle p (x) \ in \ mathbb {Z} [x], p (0) \ neq 0}$ , stopnia deg( p ) i transformację Möbiusa

${\ Displaystyle M (x) = {\ Frac {ax + b} {cx + d}} = x, \ qquad a, b, c, d \ in \ mathbb {N}.}$

Wyjście : Lista izolujących przedziałów pierwiastków dodatnich p ( x ).

   1  var  ← liczba  odmian znaku  p  (  x  )  //  Reguła znaków Kartezjusza  ; 2   jeśli  var  = 0 to  POWRÓT  ∅; 3   jeśli  var  = 1 to  RETURN  {(  a  ,  b  )} //  a  = min(  M  (0),  M  (∞)),  b  = max (  M  (0),  M  (∞)), ale jeśli  b  = ∞ ustaw  b  =    ub  , gdzie  ub  jest górną granicą wartości dodatnich pierwiastków  p  (  x  ); 4   funty  ←  idealna  dolna granica dodatnich pierwiastków  p  (  x  ); 5   jeśli  funt  ≥ 1  to  p  ←  p  (  x  +  funt  ),  M  ←  M  (  x  +  funt  ); 6   str.  01  ← (  x  + 1)    deg(  p  )  p  (  1  /  x  + 1  ),  M  01  ←  M  (  1  /  x  + 1  ) // Szukaj pierwiastków rzeczywistych w (0, 1); 7   m  ←  M  (1) // Czy 1 jest pierwiastkiem? 8   p  1∞  ←  p  (  x  + 1),  M  1∞  ←  M  (  x  + 1) // Szukaj pierwiastków rzeczywistych w (1, ∞); 9   jeśli  p  (1) ≠ 0  to wtedy  10  POWRÓT  VAS(  p  01  ,  M  01  ) ∪ VAS(  p  1∞  ,  M  1∞  ) 11  jeszcze  12  POWRÓT  VAS(  p  01  ,  M  01  ) ∪ {[  m  ,  m  ]} ∪ VAS (  p  1∞  ,  M  1 ∞  ) 13  koniec 

Uwagi

• Dla uproszczenia nie uwzględniono wkładu Strzebońskiego.
• W powyższym algorytmie z każdym wielomianem związana jest transformacja Möbiusa M ( x ).
• W wierszu 1 zastosowano regułę znaków Kartezjusza .
• Jeśli linie 4 i 5 zostaną usunięte z VAS( p , M ), wynikowy algorytm jest algorytmem wykładniczym Vincenta.
• Każde podstawienie dokonane na wielomianie p ( x ) jest również wykonywane na powiązanej transformacji Möbiusa M ( x ) (wiersze 5, 6 i 8).
• Przedziały izolacji są obliczane z transformacji Möbiusa w wierszu 3, z wyjątkiem pierwiastków całkowitych obliczanych w wierszu 7 (również 12).

Przykład VAS( p , M )

Metodę VAS stosujemy do p ( x ) = x ³ − 7 x + 7 (zauważ, że: M ( x ) = x ).

Iteracja 1

 VAS(  x  3  − 7  x  + 7,  x  ) 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników  p  (  x  ) =  x  3  − 7  x  + 7 4  lb  ← 1 // idealny niższy granica — znaleziona za pomocą  obliczenia  lb  i podstawienia(a)  x  ←  x  + 1 5  p  ←  x  3  + 3  x  2  − 4  x  + 1,  M  ←  x  + 1 6  p  01  ←  x  3  -  x  2  - 2  x  + 1,  M  01  ←  x  + 2  /  x  + 1  7  m  ← 1 8  p  1∞  ←  x  3  + 6  x  2  + 5  x  + 1,  M  1∞  ←  x  + 2 10  POWRÓT  VAS(  x  3  −  x  2  − 2  x  + 1,  x  + 2  /  x  + 1  ) ∪ VAS(  x  3  + 6  x  2  + 5  x  + 1,  x  + 2) 

Lista odstępów izolacji: { }.

Lista par { p , M } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {x ^ {3} -x ^ {2} -2x + 1, {\ tfrac {x + 2} {x + 1}} \ prawo \}, \ {x ^ {3}+6x^{2}+5x+1,x+2\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 2

 VAS(  x  3  −  x  2  − 2  x  + 1,  x  + 2  /  x  + 1  ) 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników  p  (  x  ) =  x  3  −  x  2  − 2  x  + 1 4  lb  ← 0 // idealna dolna granica — znaleziona za pomocą  obliczenia  lb  i podstawienia(ów)  x  ←  x  + 1 6  p  01  ←  x  3  +  x  2  - 2  x  - 1,  M  01  ←  2  x  + 3  /  x  + 1  7  m  ←  3  /  2  8  p  1∞  ←  x  3  + 2  x  2  -  x  - 1,  M  1∞  ←  x  + 3  /  x  + 2  10  ZWRÓĆ  VAS(  x  3  +  x  2  − 2  x  − 1,  2  x  + 3  /  x  + 2  ) ∪ VAS(  x  3  + 2  x  2  −  x  − 1,  x  + 3  /  x  + 2  ) 

Lista odstępów izolacji: { }.

Lista par { p , M } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {x ^ {3} + x ^ {2} -2x -1, {\ tfrac {2x + 3} {x + 2}} \ prawo \}, \ lewo \ { x^{3}+2x^{2}-x-1,{\tfrac {x+3}{x+2}}\right\},\{x^{3}+6x^{2}+5x +1,x+2\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 3

 VAS(  x  3  +  x  2  − 2  x  − 1,  2  x  + 3  /  x  + 2  ) 1  var  ← 1 // liczba  zmian znaku  w ciągu współczynników  p  (  x  ) =  x  3  +  x  2  − 2  x  − 1 3  POWRÓT  {(  3  /  2  , 2)} 

Lista odstępów izolacji: {( 3 / 2 , 2)}.

Lista par { p , M } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {x ^ {3} + 2x ^ {2} -x -1, {\ tfrac {x + 3} {x + 2}} \ prawo \}, \ {x ^ {3}+6x^{2}+5x+1,x+2\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 4

 VAS(  x  3  + 2  x  2  −  x  − 1,  x  + 3  /  x  + 2  ) 1  var  ← 1 // liczba  zmian znaku  w ciągu współczynników  p  (  x  ) =  x  3  + 2  x  2  −  x  − 1 3  ZWROT  {(1,  3  /  2  )} 

Lista przedziałów izolacji: {(1, 3 / 2 ), ( 3 / 2 , 2)}.

Lista par { p , M } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {x ^ {3} + 6x ^ {2} + 5x + 1, x + 2 \ prawo \} \ prawo \}.}$

Usuń pierwszy i przetwórz go.

Iteracja 5

 VAS(  x  3  + 6  x  2  + 5  x  + 1,  x  + 2) 1  var  ← 0 // liczba  zmian znaku  w ciągu współczynników  p  (  x  ) =  x  3  + 6  x  2  + 5  x  + 1 2  POWRÓT  ∅ 

Lista przedziałów izolacji: {(1, 3 / 2 ), ( 3 / 2 , 2)}.

Lista par { p , M } do przetworzenia: ∅ .

Skończone.

Wniosek

Dlatego dwa dodatnie pierwiastki wielomianu p ( x ) = x ³ - 7 x + 7 leżą wewnątrz przedziałów izolacji (1, 3 / 2 ) i ( 3 / 2 , 2) }. Każdy pierwiastek można przybliżyć (na przykład) dzieląc na pół przedział izolacji 10-6 ^, w którym się znajduje, aż różnica punktów końcowych będzie mniejsza niż ; zgodnie z tym podejściem pierwiastki okazują się ρ ₁ = 1,3569 i ρ2 = _1,69202 .

Metody bisekcji

Istnieją różne metody bisekcji wywodzące się z twierdzenia Vincenta ; wszystkie są przedstawione i porównane gdzie indziej. Poniżej opisano dwie najważniejsze z nich, a mianowicie Vincenta-Collinsa-Akritasa (VCA) oraz metodę Vincenta-Alesiny-Galuzziego (VAG) .

Metoda Vincenta – Alesiny – Galuzziego (VAG) jest najprostszą ze wszystkich metod wywodzących się z twierdzenia Vincenta, ale ma najbardziej czasochłonny test (w wierszu 1) w celu ustalenia, czy wielomian ma pierwiastki w przedziale zainteresowania; sprawia to, że jest to najwolniejsza z metod przedstawionych w tym artykule.

Natomiast metoda Vincenta-Collinsa-Akritasa (VCA) jest bardziej złożona, ale wykorzystuje prostszy test (w linii 1) niż VAG . To wraz z pewnymi ulepszeniami sprawiło, że VCA jest najszybszą metodą bisekcji.

Vincent – ​​Collins – Akritas (VCA, 1976)

Była to pierwsza metoda opracowana w celu przezwyciężenia wykładniczej natury oryginalnego podejścia Vincenta i ma dość interesującą historię, jeśli chodzi o jej nazwę. Ta metoda, która wyodrębnia pierwiastki rzeczywiste, wykorzystując regułę znaków Kartezjusza i twierdzenie Vincenta , była pierwotnie nazywana zmodyfikowanym algorytmem Uspienskiego przez jego wynalazców Collinsa i Akritasa. Po przejrzeniu nazw takich jak „Metoda Collinsa-Akritasa” i „Metoda Kartezjusza” (zbyt myląca, jeśli weźmie się pod uwagę artykuł Fouriera), w końcu François Boulier z Uniwersytetu w Lille nadał jej nazwę Vincent – ​​Collins – Akritas ( VCA ) metoda, str. 24, opierając się na fakcie, że „metoda Uspienskiego” nie istnieje, podobnie jak „metoda Kartezjusza”. Najlepsze wdrożenie tej metody zawdzięczają Rouillierowi i Zimmermanowi i do tej pory jest to najszybsza metoda bisekcji. Ma taką samą złożoność najgorszego przypadku jak algorytm Sturma, ale prawie zawsze jest znacznie szybszy. Został on zaimplementowany w Maple 's RootFinding.

Oto jak działa VCA( p , ( a , b )):

• Mając dany wielomian p _orig ( x ) stopnia deg( p ), taki że p _orig (0) ≠ 0, którego dodatnie pierwiastki muszą być izolowane, najpierw oblicz górną granicę, ub na wartościach tych dodatnich pierwiastków i ustal p ( x ) = p _orig ( ub * x ) i ( za , b ) = (0, ub ). Dodatnie korzenie p ( x ) wszystkie leżą w przedziale (0, 1) i istnieje bijekcja między nimi a pierwiastkami p _orig ( x ), które wszystkie leżą w przedziale ( a , b ) = (0, ub ) (patrz odpowiedni rysunek ); ta bijekcja jest wyrażona przez α _{( a , b )} = a + α _(0,1) ( b − a ). Podobnie istnieje bijekcja między przedziałami (0, 1) i (0, ub ).

Bijekcja między pierwiastkami p _orig ( x ) i p ( x ).

• Powtórz następujące kroki, dopóki są pary { p ( x ), ( a , b )} do przetworzenia.
• „ testu pierwiastków 0_1 ” Budana na p ( x ), aby obliczyć (używając liczby var zmian znaku w sekwencji jego współczynników) liczbę jego pierwiastków w przedziale (0, 1). Jeśli nie ma pierwiastków, zwróć zbiór pusty, ∅, a jeśli pierwiastek jest jeden, zwróć przedział ( a , b ).
• Jeśli istnieją dwie lub więcej odmian znaku, „ test pierwiastków 0_1 ” Budana implikuje, że wewnątrz przedziału (0, 1) może być zero, jeden, dwa lub więcej pierwiastków rzeczywistych. W tym przypadku przetnij to na pół i rozważ osobno pierwiastki z p ( x ) wewnątrz przedziału (0, 1 / 2 ) — które odpowiadają pierwiastkom z p _orig ( x ) wewnątrz przedziału ( a , 1 / 2 ( a + b )) z przedziału ( 1 / 2 , 1) i odpowiadają pierwiastkom z p _orig ( x ) wewnątrz przedziału ( 1 / 2 ( a + b ), b ); to znaczy przetwarzać odpowiednio pary

${\ Displaystyle \ lewo \ {2 ^ {\ stopień (p)} p ({\ tfrac {x} {2}}), (a, {\ tfrac {1} {2}} (a + b ))\prawo\},\quad \lewo\{2^{\deg(p)}p({\tfrac {1}{2}}(x+1)),({\tfrac {1}{2 }}(a+b),b)\right\}}$

(patrz odpowiedni rysunek). Równie dobrze może się okazać, że 1/2 . ( jest pierwiastkiem z p (x), w którym to przypadku 1/2 (a + b ) jest pierwiastkiem z zmniejsza się p orig x ) , _a przedział izolacji do punktu

Bijections między pierwiastkami p ( x ) i p ( x / 2 ) i p ( x + 1 / 2 ).

Poniżej znajduje się rekurencyjna prezentacja oryginalnego algorytmu VCA( p , ( a , b )).

VCA ( p , ( a , b ))

Dane wejściowe : Jednowymiarowy wielomian bez kwadratów p ( ub * x ) ∈ Z [ x ], p (0) ≠ 0 stopnia deg ( p ) i przedział otwarty ( a , b ) = (0, ub ), gdzie ub jest górną granicą wartości dodatnich pierwiastków p ( x ). (Dodatnie pierwiastki p ( ub * x ) leżą w przedziale otwartym (0, 1)). Wyjście : Lista izolujących przedziałów dodatnich pierwiastków p ( x )

   1  var  ← liczba  zmian znaku  (  x  + 1)  deg(  p  )  p  (  1  /  x  + 1 ) //   „  test pierwiastków 0_1  ”  Budana  ; 2   jeśli  var  = 0  to POWRÓT  ∅; 3   jeśli  var  = 1  to RETURN  {(  a  ,  b  )}; 4   p 0
 1  /  2  ← 2  stopnie (  str  )  p  (  x  /  2  ) // Poszukaj pierwiastków rzeczywistych w (0,  1  /  2  ); 5   m  ←  1  /  2  (  a  +  b  ) // Czy  1  /  2  to pierwiastek? 6   p 
 1  /  2  1  ← 2  deg(  p  )  p  (  x  + 1  /  2  ) // Szukaj pierwiastków rzeczywistych w (  1  /  2  , 1); 7   jeśli   p  (  1  /  2  ) ≠ 0  wtedy  8  POWRÓT  VCA (  p 0
 1  /  2  , (  a  ,  m  )) ∪ VCA (  p 
 1  /  2  1  , (  m  ,  b  )) 9  inaczej  10  POWRÓT  VCA (  p 0
 1  /  2  , (  za  ,  m  )) ∪ {[  m  ,  m  ]} ∪ VCA (  p 
 1  /  2  1  , (  m  ,  b  )) 11  koniec 

Uwaga

• W powyższym algorytmie z każdym wielomianem związany jest przedział ( a , b ). Jak pokazano w innym miejscu, str. 11, transformacja Möbiusa może być również powiązana z każdym wielomianem, w którym to przypadku VCA wygląda bardziej jak VAS .
• zastosowano „ test pierwiastków 0_1 ” Budana .

Przykład VCA( p , ( a , b ))

Mając wielomian p _orig ( x ) = x ³ − 7 x + 7 i biorąc jako górną granicę wartości pierwiastków dodatnich ub = 4 argumentami metody VCA są: p ( x ) = 64 x ³ − 28 x + 7 i ( za , b ) = (0, 4) .

Iteracja 1

 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = 7  x  3  − 7  x  2  − 35  x  + 43 4  p 0
 1  /  2  ← 64  x  3  − 112  x  + 56 5  m  ← 2 6  p 
 1  /  2  1  ← 64  x  3  + 192  x  2  + 80  x  + 8 7  p  (  1  /  2  ) = 1 8  ZWROT  VCA(64  x  3  − 112  x  + 56, (0, 2)) ∪ VCA(64  x  3  + 192  x  2  + 80  x  + 8, (2, 4)) 

Lista odstępów izolacji: { }.

Lista par { p , I } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {64x ^ {3} -112x + 56, (0,2) \ prawo \}, \ lewo \ {64x ^ {3} + 192x ^ {2} + 80x + 8 ,(2,4)\prawo\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 2

 VCA(64  x  3  − 112  x  + 56, (0, 2)) 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = 56  x  3  + 56  x  2  − 56  x  + 8 4  p 0
 1  /  2  ← 64  x  3  − 448  x  + 448 5  m  ← 1 6  p 
 1  /  2  1  ← 64  x  3  + 192  x  2  − 256  x  + 64 7  p  (  1  /  2  ) = 8 8  POWRÓT  VCA(64  x  3  − 448  x  + 448, (0, 1)) ∪ VCA(64  x  3  + 192  x  2  - 256  x  + 64, (1, 2)) 

Lista odstępów izolacji: { }.

Lista par { p , I } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {64x ^ {3} -448x + 448, (0,1) \ prawo \}, \ lewo \ {64x ^ {3} + 192x ^ {2} -256x + 64 ,(1,2)\prawo\},\lewo\{64x^{3}+192x^{2}+80x+8,(2,4)\prawo\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 3

 VCA(64  x  3  − 448  x  + 448, (0, 1)) 1  var  ← 0 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = 448  x  3  + 896  x  2  + 448  x  + 64 2  POWRÓT  ∅ 

Lista odstępów izolacji: { }.

Lista par { p , I } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {64x ^ {3} +192x ^ {2} -256x + 64, (1,2) \ prawo \}, \ lewo \ {64x ^ {3} + 192x ^ { 2}+80x+8,(2,4)\prawo\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 4

 VCA(64  x  3  + 192  x  2  − 256  x  + 64, (1, 2)) 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = 64  x  3  - 64  x  2  - 128  x  + 64 4  p 0
 1  /  2  ← 64  x  3  + 384  x  2  - 1024  x  + 512 5  m  ←  3  /  2  6  p 
 1  /  2  1  ← 64  x  3  + 576  x  2  − 64  x  + 64 7  p  (  1  /  2  ) = −8 8  POWRÓT  VCA(64  x  3  + 384  x  2  − 1024  x  + 512, (1,  3  /  2  )) ∪ VCA(64  x  3  + 576  x  2  − 64  x  − 64, (  3  /  2  , 2)) 

Lista odstępów izolacji: { }.

Lista par { p , I } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {64x ^ {3} + 384x ^ {2} -1024x + 512, \ lewo (1, {\ tfrac {3} {2}} \ prawo) \ prawo \}, \left\{64x^{3}+576x^{2}-64x-64,\left({\tfrac {3}{2}},2\right)\right\},\left\{64x^{ 3}+192x^{2}+80x+8,(2,4)\prawo\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 5

 VCA(64  x  3  + 384  x  2  − 1024  x  + 512, (1,  3  /  2  )) 1  var  ← 1 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = 512  x  3  + 512  x  2  − 128  x  − 64 3  POWRÓT  {(1,  3  /  2  )} 

Lista odstępów izolacji: {(1, 3 / 2 )}.

Lista par { p , I } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {64x ^ {3} + 576x ^ {2} -64x-64, \ lewo ({\ tfrac {3} {2}}, 2 \ prawo) \ prawo \}, \lewo\{64x^{3}+192x^{2}+80x+8,(2,4)\prawo\}\prawo\}.}$

Usuń pierwszy i przetwórz go.

Iteracja 6

VCA(64 x ³ + 576 x ² − 64 x − 64, ( 3 / 2 , 2))

 1  var  ← 1 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = −64  x  3  − 256  x  2  + 256  x  + 512 3  RETURN  {(  3  /  2  , 2)} 

Lista przedziałów izolacji: {(1, 3 / 2 ), ( 3 / 2 , 2)}.

Lista par { p , I } do przetworzenia:

${\ Displaystyle \ lewo \ {\ lewo \ {64x ^ {3} + 192x ^ {2} + 80x + 8, (2,4) \ prawo \} \ prawo \}.}$

Usuń pierwszy i przetwórz go.

Iteracja 7

 VCA(64  x  3  + 192  x  2  + 80  x  + 8, (2, 4)) 1  var  ← 0 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  1  /  x  + 1  ) = 8  x  3  + 104  x  2  + 376  x  + 344 2  POWRÓT  ∅ 

Lista przedziałów izolacji: {(1, 3 / 2 ), ( 3 / 2 , 2)}.

Lista par { p , I } do przetworzenia: ∅ .

Skończone.

Wniosek

Dlatego dwa dodatnie pierwiastki wielomianu p ( x ) = x ³ - 7 x + 7 leżą wewnątrz przedziałów izolacji (1, 3 / 2 ) i ( 3 / 2 , 2) }. Każdy pierwiastek można przybliżyć (na przykład) dzieląc na pół przedział izolacji 10-6 ^, w którym się znajduje, aż różnica punktów końcowych będzie mniejsza niż ; zgodnie z tym podejściem pierwiastki okazują się ρ ₁ = 1,3569 i ρ2 = _1,69202 .

Vincent – ​​Alesina – Galuzzi (VAG, 2000)

Zostało to opracowane jako ostatnie i jest najprostszą metodą izolacji pierwiastków rzeczywistych wywodzącą się z twierdzenia Vincenta .

Oto jak działa VAG( p , ( a , b )):

• Mając dany wielomian p ( x ) stopnia deg( p ), taki że p (0) ≠ 0, którego dodatnie pierwiastki muszą być izolowane, najpierw oblicz górną granicę, ub na wartościach tych dodatnich pierwiastków i ustal ( a , b ) = (0, ub ). Wszystkie pierwiastki dodatnie p ( x ) leżą w przedziale ( a , b ).
• Powtórz następujące kroki, gdy istnieją interwały ( a , b ) do przetworzenia; w tym przypadku wielomian p ( x ) pozostaje taki sam.
• „ testu pierwiastków a_b ” Alesiny – Galuzziego na p ( x ), aby obliczyć (używając liczby var zmian znaku w sekwencji jego współczynników) liczbę jego pierwiastków w przedziale ( a , b ). Jeśli nie ma pierwiastków, zwróć zbiór pusty, ∅, a jeśli pierwiastek jest jeden, zwróć przedział ( a , b ).
• Jeśli istnieją dwie lub więcej odmian znaku, „ test pierwiastków a_b ” Alesiny – Galuzziego implikuje, że w przedziale ( a , b ) może być zero, jeden, dwa lub więcej pierwiastków rzeczywistych . W tym przypadku przetnij to na pół i rozważ oddzielnie pierwiastki p ( x ) wewnątrz przedziału ( a , 1/2 a b ( a + b )) od pierwiastków wewnątrz przedziału ( 1 / 2 ( + ), b ); to znaczy przetwarzać odpowiednio przedziały ( a , 1 / 2 ( a + b )) i ( 1 / 2 ( a + b ), b ). Równie dobrze może się okazać, że 1/2 , w którym to przypadku przedział izolacji zmniejsza się ( a + b ) jest pierwiastkiem z p ( x ) do punktu.

Poniżej znajduje się rekurencyjna prezentacja VAG( p , ( a , b )).

VAG ( p , ( a , b )) Wejście : Jednowymiarowy wielomian bez kwadratów p ( x ) ∈ Z [ x ], p (0) ≠ 0 stopnia deg ( p ) i przedział otwarty ( a , b ) = (0, ub ), gdzie ub jest górną granicą wartości dodatnich pierwiastków p ( x ). Wyjście : Lista izolujących przedziałów dodatnich pierwiastków p ( x ).

    1  var  ← liczba  zmian znaku  (  x  + 1)  deg (  p  )  p  (  a  +  bx  /  1 +  x ) //   „  Test pierwiastków a_b  ”  Alesiny – Galuzziego  ; 2   jeśli  var  = 0  to POWRÓT  ∅; 3   jeśli  var  = 1  to RETURN  {(  a  ,  b  )}; 4   m  ←  1  /  2   (  a  +  b  ) // Podziel przedział (  a  ,  b  ) na dwie równe części; 5   jeśli  p  (  m  ) ≠ 0  wtedy  6  ZWRÓĆ  VAG(  p  , (  a  ,  m  )) ∪ VAG(  p  , (  m  ,  b  )) 7  else  8  ZWRÓĆ  VAG(  p  , (  a  ,  m  )) ∪ {[  m  ,  m  ]} ∪ VAG(  p  , (  m  ,  b  )) 9  koniec 

Uwagi

• W porównaniu z VCA powyższy algorytm jest niezwykle prosty; dla kontrastu, VAG używa czasochłonnego „testu pierwiastków a_b” , co czyni go znacznie wolniejszym niż VCA .
• Jak zauważają Alesina i Galuzzi, s. 189, istnieje wariant tego algorytmu ze względu na Donato Saeli. 1/2 . Saeli ( a + b ) zasugerował użycie mediany punktów końcowych zamiast ich punktu środkowego Wykazano jednak, że korzystanie z mediany punktów końcowych jest na ogół znacznie wolniejsze niż wersja z „punktem środkowym”.

Przykład VAG( p , ( a , b ))

Biorąc pod uwagę wielomian p ( x ) = x ³ − 7 x + 7 i biorąc pod uwagę górną granicę wartości pierwiastków dodatnich ub = 4 argumentami VAG są: p ( x ) = x ³ − 7 x + 7 oraz ( za , b ) = (0, 4).

Iteracja 1

 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  4  x  /  x  + 1  ) = 43  x  3  − 35  x  2  − 7  x  + 7 4  m  ←  1  /  2  (0 + 4) = 2 5  p  (  m  ) = 1 8  ZWRÓĆ  VAG(  x  3  − 7  x  + 7, (0, 2)) ∪ VAG(  x  3  − 7  x  + 7, (2, 4) 

Lista odstępów izolacji: {}.

Lista interwałów do przetworzenia: {(0, 2), (2, 4)}.

Usuń pierwszy i przetwórz go.

Iteracja 2

 VAG(  x  3  − 7  x  + 7, (0, 2)) 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  2  x  /  x  + 1  ) =  x  3  − 7  x  2  + 7  x  + 7 4  m  ←  1  /  2  (0 + 2) = 1 5  p  (  m  ) = 1 8  ZWRÓĆ  VAG(  x  3  − 7  x  + 7, (0, 1)) ∪ VAG(  x  3  − 7  x  + 7, (1, 2) 

Lista odstępów izolacji: {}.

Lista interwałów do przetworzenia: {(0, 1), (1, 2), (2, 4)}.

Usuń pierwszy i przetwórz go.

Iteracja 3

 VAG(  x  3  − 7  x  + 7, (0, 1)) 1  var  ← 0 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  x  /  x  + 1  ) =  x  3  + 7  x  2  + 14  x  + 7 2  POWRÓT  ∅ 

Lista odstępów izolacji: {}.

Lista interwałów do przetworzenia: {(1, 2), (2, 4)}.

Usuń pierwszy i przetwórz go.

Iteracja 4

 VAG(  x  3  − 7  x  + 7, (1, 2)) 1  var  ← 2 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  2  x  + 1  /  x  + 1  ) =  x  3  − 2  x  2  −  x  + 1 4  m  ←  1  /  2  (1 + 2) =  3  /  2  5  p  (  m  ) = −  1  /  8  8  ZWRÓĆ  VAG(  x  3  − 7  x  + 7, (1,  3  /  2  )) ∪ VAG(  x  3  − 7  x  + 7, (  3  /  2  , 2)) 

Lista odstępów izolacji: {}.

Lista interwałów do przetworzenia: {(1, 3 / 2 ), ( 3 / 2 , 2), (2, 4)}.

Usuń pierwszy i przetwórz go.

Iteracja 5

 VAG(  x  3  − 7  x  + 7, (1,  3  /  2  )) 1  var  ← 1 // liczba  zmian znaku  w ciągu współczynników 2  3  (  x  + 1)  3  p  ( 
 3  /  2  x  + 1  /  x  + 1  ) =  x  3  + 2  x  2  − 8  x  − 8 3  POWRÓT  (1,  3  /  2  ) 

Lista odstępów izolacji: {(1, 3 / 2 )}.

Lista interwałów do przetworzenia: {( 3 / 2 , 2), (2, 4)}.

Usuń pierwszy i przetwórz go.

Iteracja 6

 VAG(  x  3  − 7  x  + 7, (  3  /  2  , 2)) 1  var  ← 1 // liczba  zmian znaku  w ciągu współczynników 2  3  (  x  + 1)  3  p  ( 
 2  x  +  3  /  2  /  x  + 1  ) = 8  x  3  + 4  x  2  - 4  x  - 1 3  POWRÓT  (  3  /  2  , 2) 

Lista przedziałów izolacji: {(1, 3 / 2 ), ( 3 / 2 , 2)}.

Lista interwałów do przetworzenia: {(2, 4)}.

Usuń pierwszy i przetwórz go.

Iteracja 7

 VAG(  x  3  − 7  x  + 7, (2, 4)) 1  var  ← 0 // liczba  zmian znaku  w ciągu współczynników (  x  + 1)  3  p  (  4  x  + 2  /  x  + 1  ) = 344  x  3  + 376  x  2  + 104  x  + 8 2  POWRÓT  ∅ 

Lista przedziałów izolacji: {(1, 3 / 2 ), ( 3 / 2 , 2)}.

Lista interwałów do przetworzenia: ∅.

Skończone.

Wniosek

Dlatego dwa dodatnie pierwiastki wielomianu p ( x ) = x ³ - 7 x + 7 leżą wewnątrz przedziałów izolacji (1, 3 / 2 ) i ( 3 / 2 , 2) }. Każdy pierwiastek można przybliżyć (na przykład) dzieląc na pół przedział izolacji 10-6 ^, w którym się znajduje, aż różnica punktów końcowych będzie mniejsza niż ; zgodnie z tym podejściem pierwiastki okazują się ρ ₁ = 1,3569 i ρ2 = _1,69202 .

Zobacz też

• Własności pierwiastków wielomianowych
• Algorytm znajdowania korzeni
• Formuły Viety
• Metoda Newtona

Linki zewnętrzne

• Berkakis, Antonis: RealRoots, bezpłatna aplikacja na urządzenia z systemem Android do porównywania metody Sturma i VAS
• https://play.google.com/store/apps/details?id=org.kde.necessitas.berkakis.realroots