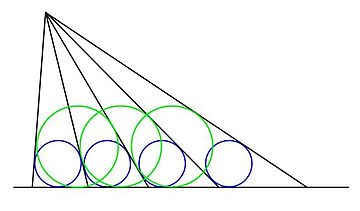
Twierdzenie o równych okręgach

Jeśli niebieskie kółka są równe, zielone kółka są również równe.

W geometrii twierdzenie o równych okręgach wywodzi się z japońskiego Sangaku i odnosi się do następującej konstrukcji: seria promieni jest rysowana od danego punktu do danej linii w taki sposób, że okręgi wpisane w trójkąty utworzone przez sąsiednie promienie i linię bazową są równe. Na ilustracji równe niebieskie kółka określają odstępy między promieniami, zgodnie z opisem.

Twierdzenie mówi, że okręgi trójkątów utworzone (zaczynając od dowolnego promienia) przez co drugi promień, co trzeci promień itd. oraz linię bazową są również równe. Przypadek każdego innego promienia jest zilustrowany powyżej zielonymi kółkami, które są równe.

Z faktu, że twierdzenie to nie zależy od kąta promienia początkowego, można zauważyć, że twierdzenie należy właściwie do analizy , a nie do geometrii, i musi odnosić się do ciągłej funkcji skalowania, która określa odstępy między promieniami. W rzeczywistości ta funkcja jest sinusem hiperbolicznym .

Twierdzenie jest bezpośrednim następstwem następującego lematu:

$,$ że n ty promień tworzy kąt normalną do linii bazowej. γ ${\ Displaystyle \ gamma _ {n}}$ jest sparametryzowany zgodnie z równaniem, $sinh \ theta _ {n}}$ ${\ Displaystyle \ theta _ {n} = a + nb}$ za $b}$ gdzie i $displaystyle$ rzeczywistymi stałymi, zdefiniuj sekwencję promieni, które spełniają warunek równych okręgów, a ponadto dowolną sekwencję promieni spełniającą warunek można utworzyć przez odpowiedni dobór stałych i za ${\ displaystyle a}$ $\ displaystyle b}$ .

Dowód lematu

$}$ diagramie linie PS i PT są sąsiednimi promieniami tworzącymi kąty i z linią PR, która jest prostopadła do $}$ linia bazowa, RST.

Linia QXOY jest równoległa do linii bazowej i przechodzi przez O , środek okręgu wpisanego w $PST$ , który jest styczny do promieni w punktach W i Z. Również linia PQ ma długość $\ displaystyle hr}$ , a linia QR ma długość ${\ displaystyle r}$ , promień okręgu.

Wtedy $△$ jest podobny do $displaystyle$ i OZY jest podobny do PQY, a z XY = XO + OY otrzymujemy △ {\ displaystyle \ trójkąt} OWX jest podobny do { $\$ $}$

{\ Displaystyle (hr) (\ tan \ gamma _ {n + 1} - \ tan \ gamma _ {n}) = r (\ sec \ gamma _ {n} + \ sec \ gamma _ {n + 1}) .}

$relacja$ na zbiorze kątów warunek

Aby udowodnić lemat, ustawiamy ${\ Displaystyle \ tan \ gamma _ {n} = \ sinh (a + nb)}$ , co daje ${\ Displaystyle \ sec \ gamma _ {n} = \ cosh (a + nb)}$ .

Za $\ Displaystyle a + (n + 1) b = (a + nb) + b}$ , stosujemy zasady dodawania dla ${\ displaystyle \ sinh }$ i ${\ displaystyle \ cosh}$ i sprawdź, czy równanie incircles jest spełnione przez ustawienie

{\ Displaystyle {\ Frac {r} {hr}} = \ tanh {\ Frac {b} {2}}.}

Daje to wyrażenie dla parametru $r}$ ${ \$ miar geometrycznych i $displaystyle$ . Dzięki tej definicji $następnie$ wyrażenie na promienie okręgów utworzonych przez przyjęcie każdego $N$ - tego promienia jako trójkątów

{\ Displaystyle {\ Frac {r_ {N}} {h-r_ {N}}} = \ tanh {\ Frac {Nb} {2}}.}

Zobacz też

Twierdzenie o równych okręgach przy przecięciu węzła
J. Tabow. Uwaga na temat twierdzenia o pięciu kołach. Magazyn Matematyka 63 (1989), 2, 92–94.