Układanka do nalewania wody

Stan początkowy standardowej układanki; dzban wypełniony 8 jednostkami wody i dwa puste dzbanki o rozmiarach 5 i 3. Rozwiązujący musi nalać wody tak, aby pierwszy i drugi dzban zawierały po 4 jednostki, a trzeci był pusty.

Zagadki z nalewaniem wody (zwane także problemami z dzbankami na wodę , problemami z przelewaniem , łamigłówkami z mierzeniem lub łamigłówkami Szklana Pułapka z Zemstą ) to klasa łamigłówek obejmująca skończony zbiór dzbanków na wodę o znanych pojemnościach całkowitych (pod względem miary cieczy , takiej jak litry lub galonów ). Początkowo każdy dzban zawiera znaną całkowitą objętość płynu, niekoniecznie równą jego pojemności.

Puzzle tego typu pytają, ile kroków trzeba przelać z jednego dzbanka do drugiego (aż jeden dzban będzie pusty, a drugi pełny), aby osiągnąć stan docelowy, określony objętością płynu, który musi się w nim znaleźć. jakiś dzban lub dzbanki.

Dzięki tożsamości Bézouta takie łamigłówki mają rozwiązanie wtedy i tylko wtedy, gdy pożądana objętość jest wielokrotnością największego wspólnego dzielnika wszystkich całkowitych objętości dzbanków.

Zasady

Powszechnym założeniem, wyrażonym jako część tych puzzli, jest to, że dzbanki w puzzlach mają nieregularny kształt i są nieoznaczone, tak że niemożliwe jest dokładne odmierzenie dowolnej ilości wody, która nie wypełnia całkowicie dzbanka. Inne założenia tych problemów mogą obejmować, że woda nie może się rozlać i że każdy etap nalewania wody z dzbanka źródłowego do dzbanka docelowego zatrzymuje się, gdy dzban źródłowy jest pusty lub dzban docelowy jest pełny, w zależności od tego, co nastąpi wcześniej.

Standardowy przykład

Standardowa układanka tego typu współpracuje z trzema dzbankami o pojemności 8, 5 i 3 litrów. Są one początkowo napełnione 8, 0 i 0 litrami. W stanie docelowym powinny być wypełnione 4, 4 i 0 litrami. Zagadkę można rozwiązać w siedmiu krokach, przechodząc przez następującą sekwencję stanów (oznaczoną jako potrójna trójka trzech objętości wody w trzech dzbankach):

[8,0,0] → [3,5,0] → [3,2,3] → [6,2,0] → [6,0,2] → [1,5,2] → [1 ,4,3] → [4,4,0].

Cowley (1926) pisze, że ta szczególna zagadka „pochodzi z czasów średniowiecza” i odnotowuje jej występowanie w XVII-wiecznym podręczniku matematyki Bacheta .

Odwracalność działań

Ponieważ zasady zezwalają tylko na zatrzymywanie/obracanie na granicach siatki kartezjańskiej (tj. przy pełnej pojemności każdego dzbanka), jedynymi działaniami odwracalnymi (odwracalnymi w jednym kroku) są:

Przelewanie wody z pełnego dzbanka do dowolnego dzbanka
Przelewanie wody z dowolnego dzbanka do pustego dzbanka

Jedynymi nieodwracalnymi działaniami, których nie można cofnąć w jednym kroku, są:

Przelewanie wody z częściowo pełnego dzbanka do innego częściowo pełnego dzbanka

Ograniczając się tylko do działań odwracalnych, możemy skonstruować rozwiązanie problemu z pożądanego wyniku. Z punktu [4,4,0] są tylko dwie czynności odwracalne: Przeniesienie 3 litrów z dzbanka 8-litrowego do pustego dzbanka 3-litrowego [1,4,3] lub przeniesienie 3 litrów z dzbanka 5-litrowego do pusty 3-litrowy dzbanek [4,1,3]. Dlatego istnieją tylko dwa rozwiązania tego problemu:

[4,4,0] ↔ [1,4,3] ↔ [1,5,2] ↔ [6,0,2] ↔ [6,2,0] ↔ [3,2,3] ↔ [3 ,5,0] ↔ [8,0,0]

[4,4,0] ↔ [4,1,3] ↔ [7,1,0] ↔ [7,0,1] ↔ [2,5, 1] ↔ [2,3,3] ↔ [5,3,0] ↔ [5,0,3] ↔ [8,0,0]

Wariant z kranami i umywalkami

Rozwiązanie zagadki z dzbankami 3 i 5 l, kranikiem i odpływem

Dwa rozwiązania na siatce kartezjańskiej, górne odpowiadające diagramowi po lewej stronie

Zasady są czasami formułowane przez dodanie kranu (źródłowego „dzbanka” z nieskończoną ilością wody) i zlewu („dzbanek” odpływowy, który przyjmuje dowolną ilość wody bez ograniczeń). Napełnienie dzbanka po brzegi z kranu lub wylanie całej zawartości dzbanka do odpływu liczy się jako jeden krok w rozwiązaniu problemu. Ta wersja układanki pojawiła się w scenie filmu Szklana pułapka z zemstą z 1995 roku . Wariant ten ma optymalne rozwiązanie, które można uzyskać za pomocą wykresu barycentrycznego w kształcie bilarda (lub bilarda matematycznego).

Wykres pokazuje dwa sposoby uzyskania 4 litrów przy użyciu 3-litrowych i 5-litrowych dzbanków oraz źródła wody i zlewu na siatce kartezjańskiej z ukośnymi liniami nachylenia −1 (takimi, że $x+y=const.$ na tych ukośnych liniach, które przedstawiają przelewanie wody z jednego dzbanka do drugiego). X i Y _ osie przedstawiają odpowiednio ilości w dzbankach 5 i 3 l. Zaczynając od (0, 0) przemierzamy siatkę wzdłuż odcinków linii, obracając się tylko na jej granicach, aż do czarnej linii oznaczającej 4 L w dzbanku 5 L. Linie ciągłe oznaczają nalewanie między dzbanami, linie przerywane oznaczają napełnianie dzbanka, a linie przerywane oznaczają opróżnianie dzbanka.

Łącząc oba rozwiązania, przejście przez linię 4 L i odwrotność drugiego rozwiązania powraca do (0, 0), dając wykres cyklu . Wtedy i tylko wtedy, gdy objętości dzbanków są względnie pierwsze , odwiedzany jest każdy punkt graniczny, dając algorytm do pomiaru dowolnej liczby całkowitej aż do sumy objętości.

Jak pokazano w poprzedniej sekcji, możemy skonstruować rozwiązanie problemu z pożądanego wyniku, używając tylko działań odwracalnych (opróżnianie pełnego dzbanka do zlewu i napełnianie pustego dzbanka z kranu są odwracalne). Aby otrzymać 4 litry z 3-litrowych i 5-litrowych dzbanów, chcemy dojść do punktu (4, 0). Od punktu (4, 0) są tylko dwie czynności odwracalne: napełnienie pustego 3-litrowego dzbanka do pełna z kranu (4,3) lub przelanie 1 litra wody z 5-litrowego dzbanka do 3-litrowego dzbanka litrowy dzbanek (1,3). Dlatego istnieją tylko dwa rozwiązania problemu:

(4, 0) ↔ (4, 3) ↔ (5, 2) ↔ (0, 2) ↔ (2, 0) ↔ (2, 3) ↔ (5, 0) ↔ (0, 0) (4

, 0) ↔ (1, 3) ↔ (1, 0) ↔ (0, 1) ↔ (5, 1) ↔ (3, 3) ↔ (3, 0) ↔ (0, 3) ↔ (0, 0)

Wykres cyklu można przedstawić za pomocą uporządkowanych par połączonych odwracalnymi działaniami:

(0, 0) ↔ (5, 0) ↔ (2, 3) ↔ (2, 0) ↔ (0, 2) ↔ (5, 2) ↔ (4, 3) ↔ (4, 0) ↔ (1 , 3) ↔ (1, 0) ↔ (0, 1) ↔ (5, 1) ↔ (3, 3) ↔ (3, 0) ↔ (0, 3) ↔ (0, 0)

który zawiera wszystkie możliwe stany osiągalne za pomocą 3-litrowego dzbanka i 5-litrowego dzbanka. Na przykład stan (1, 2) jest niemożliwy do osiągnięcia ze stanu początkowego (0, 0), ponieważ (1, 2) ma oba dzbanki częściowo pełne i z tego stanu nie jest możliwe żadne działanie odwracalne.

Dzbanek z wodą początkową

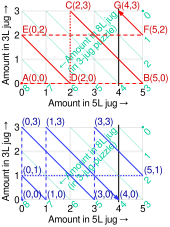
Rozpoczynając od 9 litrów w 12-litrowym dzbanku, po lewej stronie na czerwono zaznaczono roztwór na 5 litrów, a po prawej na niebiesko roztwór na 4 litry. Wszystkie ukośne linie mają to samo nachylenie -1, reprezentujące przelewanie wody z jednego dzbanka do drugiego.

Innym wariantem jest sytuacja, w której jeden z dzbanów ma na początku znaną objętość wody; W takim przypadku osiągalne objętości są albo wielokrotnością największego wspólnego dzielnika między dwoma pojemnikami od istniejącej znanej objętości, albo od zera. Na przykład, jeśli jeden dzban o pojemności 8 litrów jest pusty, a drugi o pojemności 12 litrów ma na początku 9 litrów wody, to przy źródle (kran) i odpływie (zlew) te dwa dzbanki mogą mierzyć pojemności 9 litrów, 5 litrów, 1 litr, a także 12 litrów, 8 litrów, 4 litry i 0 litrów. Najprostszym rozwiązaniem dla 5 litrów jest (9,0) → (9,8) → (12,5); Najprostszym rozwiązaniem dla 4 litrów jest (9,0) → (12,0) → (4,8). Rozwiązania te można zwizualizować za pomocą czerwonych i niebieskich strzałek w a $)$ kartezjańska z ukośnymi liniami (o nachyleniu takim, że oddalonych od siebie o 4 litry, zarówno w poziomie,

Ponownie, jeśli ograniczymy się tylko do działań odwracalnych, od pożądanego punktu (5,0) są tylko dwa działania odwracalne: przelanie 5 litrów wody z dzbanka 12-litrowego do dzbanka 8-litrowego (0,5) , lub napełnianie pustego 8-litrowego dzbanka do pełna z kranu (5,8). Dlatego istnieją tylko dwa rozwiązania problemu:

(5, 0) ↔ (0, 5) ↔ (12, 5) ↔ (9, 8) ↔ (9, 0) (5, 0) ↔ (5, 8) ↔ (12,

1) ↔ (0, 1) ↔ (1, 0) ↔ (1, 8) ↔ (9, 0)

W przypadku pytania o pojemności 4 litrów, ponieważ $na$ jest jedno nieodwracalne działanie Może to być po prostu wlanie całych 9 litrów wody z 12-litrowego dzbanka do zlewu (0,0) lub napełnienie do pełna do 12 litrów z kranu (12,0). Następnie możemy skonstruować nasze rozwiązania wstecz, jak poprzednio:

(4, 0) ↔ (4, 8) ↔ (12, 0) ← (9, 0)

(4, 0) ↔ (0, 4) ↔ (12, 4) ↔ (8, 8) ↔ (8, 0) ↔ (0, 8) ↔ (0, 0) ← (9, 0)

Rozwiązanie dla trzech dzbanków za pomocą wykresu barycentrycznego

Dwa rozwiązania standardowej układanki z wykorzystaniem wykresu barycentrycznego

Jeśli liczba dzbanków wynosi trzy, stan napełnienia po każdym kroku można opisać na diagramie współrzędnych barycentrycznych , ponieważ suma wszystkich trzech liczb całkowitych pozostaje taka sama we wszystkich krokach. W konsekwencji kroki można zobrazować jako ruchy bilarda w (przyciętym) układzie współrzędnych na trójkątnej siatce.

Wykres barycentryczny po prawej stronie daje dwa rozwiązania zagadki 8, 5 i 3 L. Żółty obszar oznacza kombinacje możliwe do osiągnięcia za pomocą dzbanków. Zaczynając od kwadratu, ciągłe czerwone i przerywane niebieskie ścieżki pokazują płynne przejścia. Kiedy wierzchołek ląduje na kropkowanym czarnym trójkącie, zmierzono 4 L. Kolejne nalanie do diamentu daje 4 litry w każdym 8 i 5 litrowym dzbanku.

Niebieska ścieżka jest o krok krótsza niż ścieżka układanki z dwoma dzbankami z kurkiem i odpływem, ponieważ w 8-litrowym dzbanku możemy zgromadzić 4 litry, których nie ma w wariancie z dwoma dzbankami.

Zobacz też

Układanka ze spalaniem liny , kolejna klasa łamigłówek polegająca na łączeniu pomiarów
Einstellung efekt

Literatura

Cowley, Elżbieta B. (1926). „Uwaga dotycząca liniowego równania diofantycznego”. Pytania i dyskusje. Amerykański miesięcznik matematyczny . 33 (7): 379–381. doi : 10.2307/2298647 . JSTOR 2298647 . MR 1520987 .
Tweedie, MCK (1939). „Graficzna metoda rozwiązywania Tartagliańskich zagadek pomiarowych”. Gazeta Matematyczna . Tom. 23, nie. 255. s. 278–282. JSTOR 3606420 .
Saksena, JP (1968). „Stochastyczne optymalne trasowanie”. Unternehmensforschung . Tom. 12, nie. 1. s. 173–177. doi : 10.1007/BF01918326 .
Atwood, Michael E.; Polson, Peter G. (1976). „Model procesu dla problemów z dzbanem na wodę”. Psychologia poznawcza . Tom. 8. s. 191–216. doi : 10.1016/0010-0285(76)90023-2 .
Rem, Marcin; Choo, młody il (1982). „Program o stałej przestrzeni o liniowej złożoności wyjściowej dla problemu trzech naczyń”. Nauka o programowaniu komputerowym . Tom. 2, nie. 2. s. 133–141. doi : 10.1016/0167-6423(82)90011-9 .
Thomas, Glanffrwd P. (1995). „Problem dzbanków na wodę: rozwiązania ze sztucznej inteligencji iz matematycznego punktu widzenia”. Matematyka w szkole . Tom. 24, nie. 2. s. 34–37. JSTOR 30215221 .
Murray-Lasso, MA (2003). „Zagadki matematyczne, potężne idee, algorytmy i komputery w nauczaniu rozwiązywania problemów” . Journal of Applied Research and Technology . Tom. 1, nie. 3. s. 215–234.
Lalczew, Zdrawko Woutow; Varbanova, Margarita Genova; Woutowa, Irirna Zdrawkowa (2009). „Geometryczna metoda Perlmana rozwiązywania problemów z nalewaniem cieczy” .
Goetschalckx, Marc (2011). „Routing pojedynczego przepływu przez sieć”. Międzynarodowa seria w badaniach operacyjnych i naukach o zarządzaniu. Tom. 161. s. 155–180. doi : 10.1007/978-1-4419-6512-7_6 .