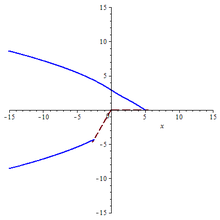
Uogólniony stożek

W matematyce uogólniony stożek jest obiektem geometrycznym określonym przez właściwość będącą uogólnieniem sum określających własność klasycznego stożka . Na przykład w geometrii elementarnej elipsę można zdefiniować jako miejsce geometryczne punktu, który porusza się po płaszczyźnie w taki sposób, że suma jego odległości od dwóch stałych punktów – ognisk – na płaszczyźnie jest stała. Krzywa uzyskana, gdy zestaw dwóch stałych punktów zostanie zastąpiony dowolnym, ale ustalonym, skończonym zbiorem punktów na płaszczyźnie, nazywana jest n-elipsą i można ją traktować jako elipsę uogólnioną. Ponieważ elipsa jest równoodległym zbiorem dwóch okręgów, równoodległy zbiór dwóch dowolnych zestawów punktów na płaszczyźnie można postrzegać jako uogólniony stożek. We współrzędnych prostokątnych kartezjańskich równanie y = x ² reprezentuje parabolę . Uogólnione równanie y = x ^r , dla r ≠ 0 i r ≠ 1, można traktować jako definiujące uogólnioną parabolę. Idea stożka uogólnionego znalazła zastosowanie w teorii aproksymacji i teorii optymalizacji .

Spośród kilku możliwych sposobów uogólnienia pojęcia stożka, najczęściej stosowanym podejściem jest zdefiniowanie go jako uogólnienia elipsy . Punktem wyjścia dla tego podejścia jest spojrzenie na elipsę jako krzywą spełniającą „właściwość dwóch ognisk”: elipsa to krzywa będąca miejscem geometrycznym punktów, których suma odległości od dwóch danych punktów jest stała. Te dwa punkty są ogniskami elipsy. Krzywą uzyskaną przez zastąpienie zestawu dwóch stałych punktów dowolnym, ale ustalonym, skończonym zbiorem punktów na płaszczyźnie można traktować jako uogólnioną elipsę. Uogólnione stożki z trzema ogniskami nazywane są elipsami trójogniskowymi. Można to dalej uogólnić na krzywe, które są otrzymywane jako loci punktów, tak że pewna ważona suma odległości od skończonego zbioru punktów jest stała. Dalsze uogólnienie jest możliwe przy założeniu, że wagi przypisane do odległości mogą mieć dowolny znak, a mianowicie plus lub minus. Wreszcie, można również usunąć ograniczenie, że zbiór punktów stałych, zwany zbiorem ognisk stożka uogólnionego, jest skończony. Można założyć, że zbiór jest skończony lub nieskończony. W przypadku nieskończonym ważoną średnią arytmetyczną należy zastąpić odpowiednią całką. Uogólnione stożki w tym sensie są również nazywane polielipsami , jajeczkami lub uogólnionymi elipsami . Ponieważ takie krzywe były rozważane przez niemieckiego matematyka Ehrenfrieda Walthera von Tschirnhausa (1651 – 1708), są one również znane jako Tschirnhaus'sche Eikurve . Również takie uogólnienia zostały omówione przez Rene Descartesa i Jamesa Clerka Maxwella.

Wieloogniskowe owalne krzywe

Konstrukcja owalu określona przez AP + 2 BP = c za pomocą szpilek, ołówka i sznurka, jak opisał James Clerk Maxwell.

Konstrukcja owalu określona przez AP + BP + CP = c za pomocą szpilek, ołówka i sznurka, jak opisał James Clerk Maxwell.

Rene Descartes (1596–1650), ojciec geometrii analitycznej, w swojej La Geometrie opublikowanej w 1637 r. Wydzielił około 15-stronicową sekcję, aby omówić to, co nazwał elipsami dwuogniskowymi. Dwuogniskowy owal $,$ jako miejsce punktu P , który porusza się w płaszczyźnie w taki sposób, że B są punktami stałymi na λ ic są stałymi, które mogą być dodatnie lub ujemne. Kartezjusz wprowadził te owale, które są obecnie znane jako owale kartezjańskie , aby określić powierzchnie szkła w taki sposób, że po załamaniu promienie spotykają się w tym samym punkcie. Kartezjusz również rozpoznał te owale jako uogólnienia stożków centralnych, ponieważ dla pewnych wartości λ owale te sprowadzają się do znanych stożków centralnych, a mianowicie koła, elipsy lub hiperboli.

Wieloogniskowe owale zostały ponownie odkryte przez Jamesa Clerka Maxwella (1831–1879), gdy był jeszcze uczniem. W wieku 15 lat Maxwell napisał pracę naukową na temat tych owali, zatytułowaną „Obserwacje figur opisanych z wieloma ogniskami i promieniami o różnych proporcjach”, którą przedstawił profesor JD Forbes na spotkaniu Royal Society w Edynburgu w 1846 r. Profesor JD Forbes opublikował również relację z artykułu w Proceedings of the Royal Society of Edinburgh. W swoim artykule, chociaż Maxwell nie użył terminu „uogólniony stożek”, rozważał krzywe zdefiniowane przez warunki, które były uogólnieniami warunku definiującego elipsę.

Definicja

Owal wieloogniskowy to krzywa zdefiniowana jako miejsce punktu poruszającego się w taki sposób

${\ Displaystyle \ lambda _ {1} A_ {1} P + \ lambda _ {2} A_ {2} P + \ cdots + \ lambda _{n}A_{n}P=c}$

gdzie A ₁ , A ₂ , . . . , An są punktami _stałymi na płaszczyźnie i λ ₁ , λ ₂ , . . . , λ _n to ustalone liczby wymierne, a c to stała. Podał proste metody rysowania takich owali za pomocą szpilki i ołówka.

Metoda rysowania owalu określonego równaniem $ilustruje$ przyjęte przez Zamocuj dwa kołki w ogniskach A i B . Weź sznurek o długości c + AB i przywiąż jeden koniec sznurka do szpilki w A . Ołówek jest przymocowany do drugiego końca sznurka, a sznurek przechodzi przez szpilkę w ognisku B. Ołówek jest następnie przesuwany, prowadzony przez zagięcie sznurka. Krzywa wykreślona ołówkiem to locus P . Jego pomysłowość jest bardziej widoczna w opisie metody rysowania trójogniskowego owalu określonego równaniem postaci ${\ Displaystyle AP + BP + CP = c}$ . Niech trzy szpilki będą zamocowane w trzech ogniskach A , B , C . Niech jeden koniec sznurka zostanie przymocowany do kołka w punkcie C i niech sznurek zostanie przeciągnięty wokół pozostałych kołków. Niech ołówek zostanie przymocowany do drugiego końca sznurka. Niech ołówek złapie zagięcie w sznurku między A i C , a następnie rozciągnij do P. Ołówek porusza się tak, że sznurek jest napięty. Wynikowa figura byłaby częścią trójogniskowej elipsy. Pozycje sznurka mogą wymagać dostosowania, aby uzyskać pełny owal.

W ciągu dwóch lat po tym, jak jego artykuł został przedstawiony Towarzystwu Królewskiemu w Edynburgu, Maxwell systematycznie rozwijał geometryczne i optyczne właściwości tych owali.

Specjalizacja i uogólnienie podejścia Maxwella

Jako szczególny przypadek podejścia Maxwella rozważ n-elipsę — miejsce punktu, który porusza się w taki sposób, że spełniony jest następujący warunek:

${\ Displaystyle A_ {1} P + A_ {2} P + \ cdots + A_ {n} P = c. \,}$

Dzieląc przez n i zastępując c / n przez c , ten warunek definiujący można określić jako

${\ Displaystyle {\ Frac {1} {n}} (A_ {1} P + A_ {2} P + \ cdots + A_ {n }P)=c}$

Sugeruje to prostą interpretację: uogólniony stożek jest krzywą taką, że średnia odległość każdego punktu P na krzywej od zbioru { A ₁ , A ₂ , . . . , An } ma taką samą stałą wartość _. To sformułowanie koncepcji uogólnionego stożka zostało dalej uogólnione na kilka różnych sposobów.

• Zmień definicję średniej . W sformułowaniu średnią zinterpretowano jako średnią arytmetyczną. Można to zastąpić innymi pojęciami średnich, takimi jak średnia geometryczna odległości. Jeśli średnia geometryczna jest używana do określenia średniej, otrzymane krzywe okazują się lemniskatami . „Lemniskaty to zbiory, których wszystkie punkty mają tę samą średnią geometryczną odległości (tj. ich iloczyn jest stały). Lemniskaty odgrywają centralną rolę w teorii aproksymacji. Aproksymacja wielomianowa funkcji holomorficznej może być interpretowana jako aproksymacja krzywe poziomów z lemniskatami. Iloczyn odległości odpowiada wartości bezwzględnej rozkładu pierwiastków wielomianów na płaszczyźnie zespolonej.
• Zmień kardynalność zbioru ogniskowego . Zmodyfikuj definicję tak, aby można było zastosować definicję nawet w przypadku, gdy ogniskowa jest nieskończona. Możliwość tę po raz pierwszy wprowadzili C. Gross i T.-K. Strempel [2] i postawili problem, czy które wyniki (klasycznego przypadku) można rozszerzyć na przypadek nieskończenie wielu ognisk, czy też na ciągły zbiór ognisk.
• Zmień wymiar przestrzeni bazowej . Można założyć, że punkty leżą w jakiejś d -wymiarowej przestrzeni.
• Zmień definicję odległości . Tradycyjnie stosowane są definicje euklidesowe. zamiast tego można zastosować inne pojęcia odległości, takie jak odległość taksówki . Uogólnione stożki z tym pojęciem odległości znalazły zastosowanie w tomografii geometrycznej .

Sformułowanie definicji stożka uogólnionego w najbardziej ogólnym przypadku, gdy liczność zbioru ogniskowego jest nieskończona, obejmuje pojęcia zbiorów mierzalnych i całki Lebesgue'a. Wszystkie one zostały wykorzystane przez różnych autorów, a uzyskane krzywe zostały zbadane ze szczególnym uwzględnieniem zastosowań.

Definicja

Niech $rightarrow R}$$\$ będzie metryką i na zbiorze zwartym ${\ Displaystyle K \ podzbiór R ^ {n}}$ z ${\ Displaystyle \ mu (K)> 0}$ . Nieważona uogólniona funkcja stożkowa ${\ displaystyle K}$ z jest ${\ displaystyle K}$

${\ Displaystyle f_ {K} (x) = \ int _ {K} g (x, y) d (x, y)\,d_{\mu }y}$

gdzie ${\ displaystyle g: R ^ {n} \ razy R ^ {n} \ rightarrow R}$ jest funkcją jądra powiązaną z ${\ displaystyle f_ {K}}$ . ${\ displaystyle K}$ to zbiór ognisk. $_$ poziomów _

Uogólnione stożki za pomocą równań biegunowych

Rysunek przedstawia położenie początkowe prawego okrągłego stożka wraz z płaskim przekrojem przed rozwinięciem go na płaszczyznę.

Rysunek przedstawia dowolne położenie prawego okrągłego stożka wraz z płaskim przekrojem podczas odwijania stożka na płaszczyznę. Rysunek pokazuje również uogólniony stożek (kropkowana krzywa na płaszczyźnie), do którego przekrój stożkowy na stożku jest rozwijany w płaszczyźnie.

Biorąc pod uwagę stożek, wybierając ognisko stożka jako biegun i linię przechodzącą przez biegun poprowadzoną równolegle do kierownicy stożka jako oś biegunową, równanie biegunowe stożka można zapisać w następującej postaci:

${\ Displaystyle R = {\ Frac {ed} {1 + e \ sin \ teta}}}$

Tutaj e jest ekscentrycznością stożka, a d jest odległością kierownicy od bieguna. Tom M. Apostol i Mamikon A. Mnatsakanian w swoich badaniach krzywych narysowanych na powierzchniach prawych okrągłych stożków wprowadzili nową klasę krzywych, które nazwali uogólnionymi stożkami. Są to krzywe, których równania biegunowe są podobne do równań biegunowych zwykłych stożków, a zwykłe stożki pojawiają się jako szczególne przypadki tych uogólnionych stożków.

Definicja

₀ Dla stałych r ≥ 0, λ ≥ 0 i rzeczywistych k , płaska krzywa opisana równaniem biegunowym

${\ Displaystyle R = {\ Frac {r_ {0}} {1 + \ lambda \ sin (k \ teta)}}}$

nazywamy stożkiem uogólnionym . Stożek nazywany jest uogólnioną elipsą, parabolą lub hiperbolą zgodnie z λ <1, λ = 1 lub λ > 1.

Przypadki specjalne

• W szczególnym przypadku, gdy k = 1, uogólniony stożek redukuje się do zwykłego stożka.
• W szczególnym przypadku, gdy k > 1, istnieje prosta geometryczna metoda generowania odpowiedniego uogólnionego stożka.

Niech α będzie takim kątem, że sin α = 1/ k . Rozważ prawy okrągły stożek o kącie pół-pionowym równym α . Rozważmy przecięcie tego stożka przez płaszczyznę taką, że to przecięcie jest stożkiem o mimośrodzie λ . Rozwiń stożek do samolotu. Wtedy krzywa w płaszczyźnie, do której odwijany jest stożkowy przekrój mimośrodu λ , jest uogólnionym stożkiem z równaniem biegunowym, jak określono w definicji.

• W szczególnym przypadku, gdy k <1, uogólnionego stożka nie można uzyskać przez rozwinięcie przekroju stożka. W tym przypadku istnieje inna interpretacja.

Rozważmy zwykły stożek narysowany na płaszczyźnie. Zawiń płaszczyznę, aby utworzyć prawy okrągły stożek, tak aby stożek stał się krzywą w przestrzeni trójwymiarowej. Rzut krzywej na płaszczyznę prostopadłą do osi stożka będzie stożkiem uogólnionym w sensie Apostola i Mnatsakana z k < 1.

Przykłady

0 r = 5, λ = 0,6, k = 1,5	0 r = 5, λ = 0,22, k = 5,5	0 r = 5, λ = 1, k = 1,5	0 r = 5, λ = 1, k = 1,15
0 r = 5, λ = 1,6, k = 1,5	0 r = 5, λ = 0,8, k = 0,5	0 r = 5, λ = 1,0, k = 0,5	0 r = 5, λ = 1,5, k = 0,5

Uogólnione stożki w aproksymacji krzywej

W 1996 Ruibin Qu wprowadził nowe pojęcie stożka uogólnionego jako narzędzia do generowania przybliżeń krzywych. Punktem wyjścia dla tego uogólnienia jest wynik, że sekwencja punktów ${\ Displaystyle \ {P_ {k}: k = 0,1,2, \ ldots \}}$ określony przez

${\ Displaystyle P_ {k + 1} = 2 \ alfa P_ {k} -P_ {k-1}}$

leżeć na stożku. W tym podejściu uogólniony stożek jest teraz zdefiniowany jak poniżej.

Definicja

$displaystyle$ dwa punkty i $P_$${1}}$ , to punkty te generowane przez relację rekurencyjną

${\ Displaystyle P_ {k + 1} = 2 \ alfa P_ {k} + \ beta P_ {k-1}}$

dla niektórych i spełniających relacje ${\ displaystyle \$$}$

${\ Displaystyle \ alfa \ beta \ neq 0, \ quad (\ alfa, \ beta) \ neq (\ pm 1, -1),\quad \alpha ^{2}+\beta \neq 0}$

też na nim są.

Uogólnione stożki jako zbiory równoodległe

Animacja przedstawiająca generowanie elipsy jako równoodległego zestawu dwóch okręgów.

Definicja

Niech ( X , d ) będzie przestrzenią metryczną i niech A będzie niepustym podzbiorem X . Jeśli x jest punktem w X , odległość x od A jest zdefiniowana jako d ( x , A ) = inf{ d ( x , a ): a w A }. Jeśli A i B są niepustymi podzbiorami X , to równoodległy zbiór określony przez A i B jest zdefiniowany jako zbiór { x w X : d ( x , A ) = d ( x , B )}. Ten równoodległy zestaw jest oznaczony przez { A = B }. Termin uogólniony stożek jest używany do określenia ogólnego zestawu równoodległych.

Przykłady

Klasyczne stożki mogą być realizowane jako zestawy równoodległe. Na przykład, jeśli A jest zbiorem singletonowym, a B jest linią prostą, to zbiór równoodległy { A = B } jest parabolą. Jeśli A i B są okręgami takimi, że A mieści się całkowicie w obrębie B , to równoodległy zbiór { A = B } jest elipsą. Z drugiej strony, jeśli A leży całkowicie poza B , równoodległy zbiór { A = B } jest hiperbolą.

Dalsza lektura

• Szczegółowe omówienie uogólnionych stożków z punktu widzenia geometrii różniczkowej można znaleźć w rozdziale dotyczącym uogólnionych stożków w książce Convex Geometry autorstwa Csaby Vincze, dostępnej online.