Współrzędne zejścia

Zejście współrzędnych to algorytm optymalizacji , który sukcesywnie minimalizuje wzdłuż kierunków współrzędnych, aby znaleźć minimum funkcji. W każdej iteracji algorytm określa współrzędne lub blok współrzędnych za pomocą reguły wyboru współrzędnych, a następnie dokładnie lub niedokładnie minimalizuje odpowiednią hiperpłaszczyznę współrzędnych, jednocześnie ustalając wszystkie inne współrzędne lub bloki współrzędnych. Wyszukiwanie linii wzdłuż kierunku współrzędnych można przeprowadzić w bieżącej iteracji, aby określić odpowiedni rozmiar kroku. Zejście współrzędnych ma zastosowanie zarówno w kontekstach różniczkowych, jak i pozbawionych pochodnych.

Opis

Zejście współrzędnych opiera się na założeniu, że minimalizację funkcji wielu zmiennych można osiągnąć minimalizując ją wzdłuż jednego kierunku na raz, tj. $w$ co najmniej dużo prostsze) problemy optymalizacyjne w pętli. W najprostszym przypadku cyklicznego opadania współrzędnych , cyklicznie iteruje się przez kierunki, po jednym na raz, minimalizując funkcję celu w odniesieniu do każdego kierunku współrzędnych w danym momencie. Oznacza to, że zaczynając od początkowych wartości zmiennych

${\ Displaystyle \ mathbf {x} ^ {0} = (x_ {1} ^ {0}, \ ldots, x_ {n} ^ {0})}$ ,

k $1$$^ {k + 1}}$$}$ { \ Displaystyle problemy optymalizacji pojedynczej zmiennej

${\ Displaystyle x_{i}^{k+1}={\underset {y\in \mathbb {R}}}{\operatorname {arg\,min}}}\;f(x_{1}^{k+1}, \dots ,x_{i-1}^{k+1},y,x_{i+1}^{k},\dots ,x_{n}^{k})}$

dla każdej zmiennej z ${\ displaystyle$$\ mathbf {x}}$ , dla ${\ displaystyle i}$ od 1 do $\ displaystyle n}$ .

$mathbf {$ od początkowego zgadywania $displaystyle \$ i x $^ {0}$ iteracyjnie.

Wykonując wyszukiwanie linii w każdej iteracji, automatycznie

${\ Displaystyle F (\ mathbf {x} ^ {0}) \ geq F (\ mathbf {x} ^ {1}) \ geq F (\ mathbf {x} ^ {2}) \ geq \ kropki.}$

Można wykazać, że ta sekwencja ma podobne właściwości zbieżności jak najbardziej strome zejście. Brak poprawy po jednym cyklu wyszukiwania linii wzdłuż kierunków współrzędnych oznacza osiągnięcie punktu stacjonarnego.

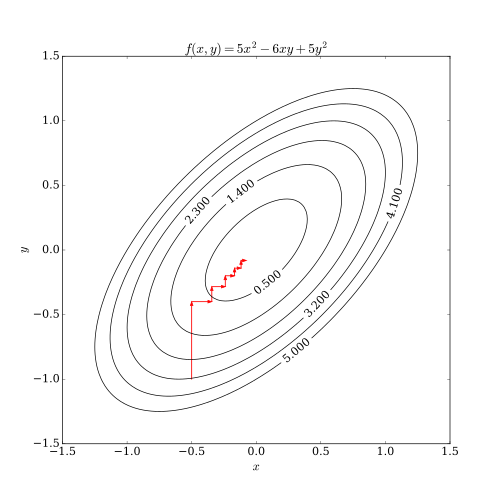
Ten proces jest zilustrowany poniżej.

Przypadek różniczkowalny

W przypadku funkcji różniczkowalnej w sposób ciągły F algorytm opadania współrzędnych można naszkicować jako:

• Wybierz początkowy wektor parametrów x .
• Do momentu osiągnięcia zbieżności lub dla pewnej ustalonej liczby iteracji:
  • Wybierz indeks i od 1 do n .
  • Wybierz wielkość kroku α .
  • Zaktualizuj x _ja do x _ja - α ∂ fa / ∂ x _ja ( x ) .

Wielkość kroku można wybrać na różne sposoby, np. przez znalezienie dokładnego minimalizatora f ( x _i ) = F ( x ) (tj. F ze wszystkimi zmiennymi z wyjątkiem x _i ustalonego) lub za pomocą tradycyjnych kryteriów wyszukiwania liniowego.

Ograniczenia

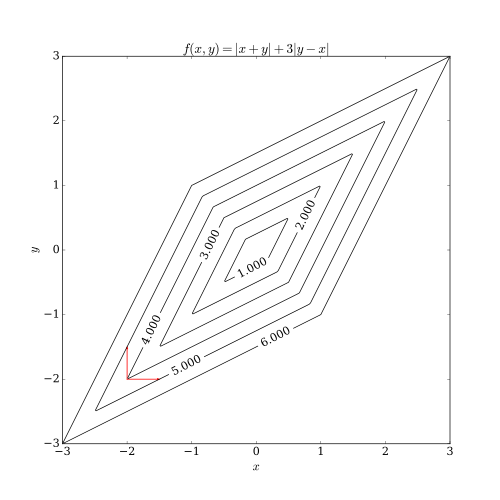
Zejście współrzędnych ma dwa problemy. Jednym z nich jest posiadanie niegładkiej funkcji wielu zmiennych. Poniższy rysunek pokazuje, że iteracja zejścia współrzędnych może utknąć w niestacjonarnym punkcie , jeśli krzywe poziomów funkcji nie są gładkie. Załóżmy, że algorytm znajduje się w punkcie (-2, -2) ; następnie istnieją dwa kierunki wyrównane do osi, które może wziąć pod uwagę przy wykonywaniu kroku, wskazane przez czerwone strzałki. Jednak każdy krok w tych dwóch kierunkach zwiększy wartość funkcji celu (zakładając problem minimalizacji), więc algorytm nie wykona żadnego kroku, mimo że oba kroki razem zbliżyłyby algorytm do optimum. Chociaż ten przykład pokazuje, że zejście współrzędnych niekoniecznie jest zbieżne do optimum, możliwe jest wykazanie zbieżności formalnej w rozsądnych warunkach.

Innym problemem jest trudność w równoległości. Ponieważ natura zejścia współrzędnych polega na cyklicznym przechodzeniu przez kierunki i minimalizowaniu funkcji celu w odniesieniu do każdego kierunku współrzędnych, zejście współrzędnych nie jest oczywistym kandydatem na masywną równoległość. Ostatnie prace badawcze wykazały, że masywna równoległość ma zastosowanie do opadania współrzędnych poprzez złagodzenie zmiany funkcji celu w odniesieniu do każdego kierunku współrzędnych.

Aplikacje

Algorytmy zejścia współrzędnych są popularne wśród praktyków ze względu na ich prostotę, ale ta sama właściwość skłoniła badaczy zajmujących się optymalizacją w dużej mierze ignorowania ich na rzecz bardziej interesujących (skomplikowanych) metod. Wczesne zastosowanie optymalizacji zejścia współrzędnych miało miejsce w dziedzinie tomografii komputerowej, gdzie stwierdzono szybką zbieżność, a następnie zostało użyte do klinicznej rekonstrukcji tomografii komputerowej metodą wielowarstwowego skanowania spiralnego. Algorytm cyklicznego opadania współrzędnych (CCD) został zastosowany do przewidywania struktury białek. Co więcej, wzrosło zainteresowanie wykorzystaniem zejścia współrzędnych wraz z pojawieniem się wielkoskalowych problemów w uczeniu maszynowym , gdzie zejście współrzędnych okazało się konkurencyjne w stosunku do innych metod w przypadku zastosowania do takich problemów, jak uczenie maszyn z liniowymi wektorami nośnymi (patrz LIBLINEAR ) i nieujemna faktoryzacja macierzy . Są atrakcyjne w przypadku problemów, w których obliczenie gradientów jest niewykonalne, być może dlatego, że wymagane do tego dane są rozproszone w sieciach komputerowych.

Zobacz też

• Adaptacyjne zejście współrzędnych
• Gradient sprzężony
• Zejście gradientowe
• Wyszukiwanie linii
• Optymalizacja matematyczna
• Metoda Newtona
• Stochastyczne zejście gradientowe - wykorzystuje jeden przykład na raz, a nie jedną współrzędną

•   Bezdek, JC; Hathaway, RJ; Howard, RE; Wilson, Kalifornia; Windham, MP (1987), „Analiza zbieżności lokalnej zgrupowanej wersji zmiennej współrzędnych”, Journal of Optimization Theory and Applications , Kluwer Academic/Plenum Publishers, tom. 54, nr. 3, s. 471–477, doi : 10.1007/BF00940196 , S2CID 120052975
•   Bertsekas, Dimitri P. (1999). Programowanie nieliniowe, wydanie drugie Athena Scientific, Belmont, Massachusetts. ISBN 1-886529-00-0 .
•   Luo, Zhiquan; Tseng, P. (1992), „O zbieżności metody zejścia współrzędnych dla minimalizacji różniczkowej wypukłej”, Journal of Optimization Theory and Applications , Kluwer Academic/Plenum Publishers, tom. 72, nr. 1, s. 7–35, doi : 10.1007/BF00939948 , hdl : 1721.1/3164 , S2CID 121091844 .
•   Wu, TongTong; Lange, Kenneth (2008), „Algorytmy zejścia współrzędnych dla regresji z karą Lasso”, The Annals of Applied Statistics , Instytut Statystyki Matematycznej, tom. 2, nie. 1, s. 224–244, arXiv : 0803.3876 , doi : 10.1214/07-AOAS147 , S2CID 16350311 .
•   Richtarik, Piotr; Takac, Martin (kwiecień 2011), „Złożoność iteracji losowych metod opadania współrzędnych bloków w celu minimalizacji funkcji złożonej”, Programowanie matematyczne , Springer, tom. 144, nr. 1–2, s. 1–38, arXiv : 1107.2848 , doi : 10.1007/s10107-012-0614-z , S2CID 16816638 .
• Richtarik, Piotr; Takac, Martin (grudzień 2012), „Metody równoległego opadania współrzędnych do optymalizacji dużych zbiorów danych”, ArXiv: 1212,0873 , arXiv : 1212,0873 .