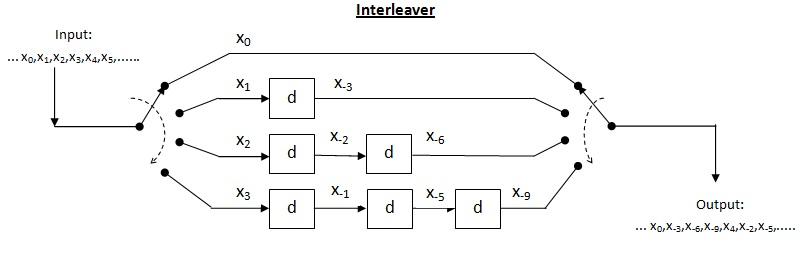
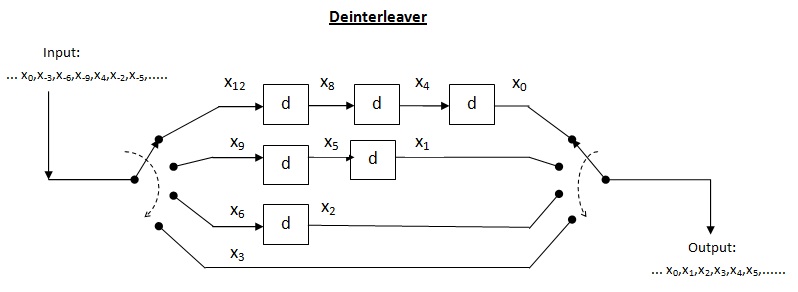
Wybuchowy kod korygujący błędy

W teorii kodowania kody korygujące błędy seryjne wykorzystują metody korekcji błędów seryjnych , które są błędami występującymi w wielu kolejnych bitach, a nie występującymi w bitach niezależnie od siebie .

Wiele kodów zostało zaprojektowanych w celu poprawiania przypadkowych błędów . Czasami jednak kanały mogą wprowadzać błędy, które są zlokalizowane w krótkim odstępie czasu. Takie błędy występują w serii (nazywanej błędami serii ), ponieważ występują w wielu kolejnych bitach. Przykłady błędów serii można znaleźć obszernie w nośnikach pamięci. Błędy te mogą być spowodowane fizycznym uszkodzeniem, takim jak rysa na płycie lub uderzenie pioruna w przypadku kanałów bezprzewodowych. Nie są niezależni; mają tendencję do koncentracji przestrzennej. Jeśli jeden bit ma błąd, prawdopodobne jest, że sąsiednie bity również mogą być uszkodzone. Metody stosowane do korygowania błędów przypadkowych są nieskuteczne w korygowaniu błędów serii.

Definicje

Wybuch długości 5

Wybuch długości ℓ

${\ Displaystyle Y = C + E.} Następnie$ że słowo kodowe $do$ przesyłane i odbierane jako $E$ błędu nazywany jest wybuchem długości, $\ displaystyle$ niezerowe składowe mi $}$ są ograniczone do $} \displaystyle \ell }$ kolejne komponenty. Na przykład ${\ Displaystyle E = (0 {\ textbf {1000011}} 0)}$ to seria o długości ${\ Displaystyle \ ell = 7.}$

Chociaż ta definicja jest wystarczająca do opisania, czym jest błąd serii, większość narzędzi opracowanych do korekcji błędów serii opiera się na kodach cyklicznych. To motywuje naszą następną definicję.

Cykliczny wybuch długości ℓ

$cyklicznie$ błędu nazywany $. Na przykład$ cyklicznym błędem serii o długości $jeśli$ jego niezerowe składowe są ograniczone do kolejnych składowych $Displaystyle \ ell =$ wcześniej wektor błędu jest cyklicznym impulsem o długości $}$ że błąd zaczyna się od ${\ Displaystyle 6}$ i kończąc na pozycji ${\ Displaystyle 1}$ . Zauważ, że indeksy są ${\ displaystyle 0}$ , to znaczy, że pierwszy element znajduje się na pozycji ${\ displaystyle 0}$ .

W pozostałej części tego artykułu będziemy używać terminu impuls w odniesieniu do cyklicznego wybuchu, o ile nie zaznaczono inaczej.

Opis wybuchu

Często przydatna jest zwięzła definicja błędu serii, która obejmuje nie tylko jego długość, ale także wzór i lokalizację takiego błędu. Definiujemy opis wybuchu jako krotkę, gdzie $P, L)$ wzorcem błędu (czyli ciągiem symboli rozpoczynającym się od pierwszego niezerowego wpisu w $\ Displaystyle$ wzorzec błędu i kończący się ostatnim niezerowym symbolem), a $.$ lokalizacja w słowie kodowym, w której można znaleźć serię

$\ Displaystyle D$ przykład opis serii wzorca błędu to re ${$ 1000011,1 $że$ , ponieważ błąd serii. Ogólnie rzecz biorąc, jeśli liczba niezerowych składników w $,$ to będzie miała różne opisy wybuchów $, z$ od innego niezerowego wpisu mi ${ \$$}$${\ Displaystyle E}$ . Aby zaradzić problemom wynikającym z niejednoznaczności opisów wybuchów za pomocą poniższego twierdzenia, jednak zanim to zrobimy, najpierw potrzebujemy definicji.

Definicja. Liczba symboli w danym wzorcu $oznaczona$ przez ${\ Displaystyle \ operatorname {długość} (y).}$

Twierdzenie (niepowtarzalność opisów wybuchów) $-$$\ Displaystyle (P_ {1}, L_ {1} })}$ , że jest wektorem błędu o długości $($ dwoma opisami wybuchów i ${\ Displaystyle (P_ {2}, L_ {2})}$ . l ${\ Displaystyle \ operatorname {długość} (P_ {1}) + \ operatorname {długość} (P_$ to oba opisy są identyczne, to znaczy ich składowe są równoważne.

Dowód

Niech będzie $displaystyle$ Hamminga (lub liczbą niezerowych wpisów) mi $E}$ . Wtedy ${\ displaystyle E}$$błędów$ dokładnie opisy . $_$ do _ Zakładamy więc, że $i$ są identyczne. Zauważamy, że każdy niezerowy wpis pojawi się we wzorcu, a więc składowe nieuwzględnione we wzorcu utworzą cykliczny ciąg zer, rozpoczynający się po ostatnim niezerowym wpisie mi { $E$$displaystyle$ i kontynuując tuż przed pierwszym niezerowym wpisem wzorca. Zbiór wskaźników odpowiadający temu przebiegowi nazywamy przebiegiem zerowym. Od razu zauważamy, że każdy opis sekwencji ma skojarzony z nim przebieg zerowy i że każdy przebieg zerowy jest rozłączny. Ponieważ mamy $przebiegi zerowe, a każdy$$nich jest rozłączny$ mamy w sumie we wszystkich przebiegach zerowych. Z drugiej strony mamy:

$${\ Displaystyle {\ rozpocząć {wyrównane} nw = {\ tekst {liczba zer w}} E & \ geqslant (n- \ operatorname {długość} (P_ {1})) + (n- \ operatorname { długość} (P_{2}))\\&=2n-\left(\mathrm {długość} (P_{1})+\mathrm {długość} (P_{2})\right)\\&\geqslant 2n -(n+1)&&\mathrm {długość} (P_{1})+\mathrm {długość} (P_{2})\leqslant n+1\\&=n-1\end{wyrównane}}}$$

Jest to sprzeczne z $są$ , że opisy błędów serii

Konsekwencją powyższego twierdzenia jest to, że nie możemy mieć dwóch różnych opisów wybuchów dla wybuchów o długości ${\ Displaystyle {\ tfrac {1} {2}} (n + 1).}$

Kody cykliczne do korekcji błędów serii

Kody cykliczne $displaystyle \ mathbb {F} _ {q}}$ zdefiniowane w następujący sposób: pomyśl o symbolach jako elementach w ${\$ . Teraz możemy myśleć o słowach jako wielomianach nad gdzie poszczególne symbole słowa odpowiadają $.$ Aby zdefiniować kod cykliczny, wybieramy ustalony wielomian, zwany wielomianem generatora . Słowa kodowe tego kodu cyklicznego to wszystkie wielomiany, które są podzielne przez ten wielomian generatora.

Słowa kodowe to wielomiany stopnia ${\ Displaystyle \ leqslant n-1}$ . Załóżmy, że wielomian generatora ma stopień $displaystyle$$g (x)}$ . Wielomiany stopnia ${\ Displaystyle \ leqslant n-1}$ , które są podzielne przez wielomiany $Displaystyle$$}$ stopień ${\ Displaystyle \ leqslant n-1-r}$ . Mamy $_$ . Każdemu z nich odpowiada słowo kodowe. Dlatego ${\ displaystyle k = nr}$ dla kodów cyklicznych.

Kody cykliczne mogą wykryć wszystkie serie długości do ${\ displaystyle \ ell = nk = r}$ . Zobaczymy później, że zdolność wykrywania błędów serii dowolnego $\$$}$ { . Kody cykliczne są uważane za optymalne do wykrywania błędów serii, ponieważ spełniają tę górną granicę:

Twierdzenie (zdolność do korekcji cyklu cyklicznego) - Każdy kod $cykliczny$ z wielomianem generatora stopnia wykryć wszystkie impulsy o długości ${\ Displaystyle \ leqslant r.}$

Dowód

$)$ że jeśli dodamy serię długości do $.$ do wielomianu podzielnego to nie będzie słowem kodowym (tj. odpowiedni wielomian nie jest podzielny przez ${\ Displaystyle g (x)}$ ). Wystarczy pokazać, że żaden wybuch długości nie $podzielny$ przez ${\ displaystyle g (x)$ . $postać$ wybuch ${\ Displaystyle \ deg (b (x)} <r.}$ gdzie Dlatego ${\ Displaystyle b (x)}$ nie jest podzielne przez ${\ Displaystyle g (x)}$ (ponieważ ten ostatni ma stopień ${\ displaystyle r}$ ). ${\ displaystyle g (x)}$ nie jest podzielna przez (w przeciwnym razie wszystkie słowa kodowe zaczynałyby się od {\ $displaystyle$$0}$ ) Dlatego $x$ nie jest podzielna przez $g (x)}$ Displaystyle

${\ Displaystyle \ leqslant n-1}$ wielomian stopnia ), oblicz resztę tego słowa po podzieleniu ⩽ przez ${\ Displaystyle g (x)}$ . Jeśli reszta $) ,$ zero (tj. jeśli słowo jest podzielne przez słowo kodowe. W przeciwnym razie zgłoś błąd. Aby poprawić ten błąd, odejmij tę resztę od transmitowanego słowa. Wynik odejmowania będzie podzielny przez $)$ będzie to poprawne słowo

Przez górną granicę wykrywania błędów serii ( $wiemy,$ cykliczny nie może wykryć serii długości $\ ell >r}$ . Jednak kody cykliczne mogą rzeczywiście wykryć większość serii o długości ${\ displaystyle > r}$ . Powodem jest to, że wykrywanie kończy się niepowodzeniem tylko wtedy, gdy seria jest podzielna przez ${\ Displaystyle g (x)}$ . Ponad alfabetami binarnymi istnieją serie długości ${\ Displaystyle 2 ^ {\ ell$ -2 $}$$)$ nich tylko $x)$ x } $.$ niepowodzenia wykrywania jest bardzo małe ( $przy$ założeniu jednolitego rozkładu we wszystkich

Rozważymy teraz fundamentalne twierdzenie dotyczące kodów cyklicznych, które pomoże w projektowaniu wydajnych kodów korygujących błędy serii poprzez kategoryzowanie serii według różnych cosetów.

$leżą$ ( odrębne Cosets ) - Kod liniowy jest $\ ell}$ korygującym błędy serii, jeśli wszystkie błędy serii długości w $\ Displaystyle$ odrębne zestawy . do ${\ displaystyle C$ .

Dowód

Niech ${\ Displaystyle \ mathbf {e} _ {1}, \ mathbf {e} _ {2}}$ będą odrębnymi błędami serii o długości ${\ Displaystyle \ leqslant \ ell},$ które leżą w tym samym zestawie kodu do ${\ displaystyle C$ . Wtedy ${\ Displaystyle \ mathbf {c} = \ mathbf {e} _ {1} - \ mathbf {e} _ {2}}$ jest słowem kodowym. Dlatego $do {\ displaystyle \ mathbf {$ zdekodować albo do ${\ displaystyle \ mathbf {0}}$ , albo $}}$ . W przeciwieństwie do tego, jeśli wszystkie błędy serii mi $Displaystyle \ mathbf {e} _ {1}}$$i$ nie leżą w tym samym zestawie, to każdy błąd jest określony przez jego syndrom. Błąd można następnie naprawić poprzez jego syndrom. Zatem kod liniowy $w$ kodem korygującym błędy wtedy i tylko wtedy, gdy wszystkie błędy serii o długości $\ ell}$ odrębnych $Displaystyle$ zestawy do . do $\ displaystyle C}$ .

Twierdzenie (klasyfikacja słowa kodowego błędu serii) $. Wtedy$$Niech$ będzie liniowym kodem korygującym błędy $nie$ długości może być słowem kodowym.

Dowód

Niech $będzie$ słowem kodowym z wybuchem długości $\ Displaystyle \ leqslant 2 \ ell}$ . Ma więc wzór ${\ Displaystyle (0,1, u, v, 1,0)}$ , gdzie i są słowami ${\ displaystyle u}$ i ${\ displaystyle v}$ długości ${\ Displaystyle \ leqslant \ ell -1.}$ Stąd słowa ${\ Displaystyle w = (0,1, u, 0,0,0 )}$ i ${\ Displaystyle cw = (0,0,0, v, 1,0)}$ to dwa serie długości ${\ Displaystyle \ leqslant \ ell}$ . W przypadku binarnych kodów liniowych należą one do tego samego zbioru. $może$ wybuch długości nie słowem kodowym.

Granice korekcji błędów wybuchu

Górne granice wykrywania i korekcji błędów serii

Przez górną granicę rozumiemy granicę naszej zdolności wykrywania błędów, której nigdy nie możemy przekroczyć. $,$ że chcemy zaprojektować kod, który błędy serii o ${\ displaystyle \ leqslant \ ell.}$ Naturalnym pytaniem, które należy zadać, jest: biorąc pod uwagę $,$ k $\ displaystyle k}$$jakie$ maksimum , którego nigdy nie możemy osiągnąć poza? Innymi słowy, jaka jest górna granica długości $}$ , które możemy wykryć za pomocą dowolnego kodu? ${\ displaystyle (n, k)$ Odpowiedzi na to pytanie dostarcza następujące twierdzenie.

$kodu$ wykrywania błędów serii) - Zdolność ${\ Displaystyle \ ell \ leqslant nk.}$ błędów serii

Dowód

Najpierw zauważamy, że kod może wykryć wszystkie serie długości wtedy i tylko wtedy $,$ gdy żadne dwa słowa kodowe nie różnią się serią długości $ell}$ . Załóżmy, że mamy dwa słowa kodowe $b$ różniące się serią $\ Displaystyle \ mathbf {c} _ {2}}$$\ Displaystyle \ mathbf { b} }$ długości ${\ Displaystyle \ leqslant \ ell}$ . Po otrzymaniu ${\ Displaystyle \ mathbf {c}$ możemy stwierdzić, czy przesłane słowo jest rzeczywiście bez błędów transmisji, czy też do $_$ jest to błąd $który$$.$ podczas transmisji Załóżmy teraz, że każde dwa słowa kodowe różnią się o więcej niż serię długości ${\ Displaystyle \ ell.}$ Nawet jeśli przesłane słowo kodowe zostanie trafione ${\ Displaystyle \ mathbf {b}}$ serię $c} _ {1}$ o długości $} }$ , nie zmieni się na inne poprawne słowo kodowe. Po otrzymaniu go możemy stwierdzić, że $jest$ wybuchem ${\ Displaystyle \ mathbf {b}.}$$pierwszych$ obserwacji wiemy, że żadne dwa słowa kodowe nie mogą dzielić . Powodem jest to, że nawet jeśli różnią się one wszystkimi innymi symbolami, nadal będą się różnić o serię długości ${\ Displaystyle \ ell.}$$\ displaystyle \ ell}$$Dlatego$ liczba ${\ Displaystyle q ^ {k} \ leqslant q ^ {n- \ ell}.}$ spełnia Stosując ${\ Displaystyle \ log _ {q}}$ po obu stronach i przestawiając, widzimy, że ${\ styl wyświetlania \ell \leqslant nk}$ .

Teraz powtarzamy to samo pytanie, ale dla korekty błędów: biorąc pod uwagę $displaystyle$ k {\ $k}$ , jaka jest górna granica długości serii, które możemy poprawić za pomocą dowolnego ${\ displaystyle \ ell$${\ Displaystyle (n, k)}$ kod? Wstępną odpowiedź na to pytanie daje następujące twierdzenie:

$\ Displaystyle \ell \leqslant nk-\log _{q}(n-\ell )+2}$ Zdolność korekcji błędów serii) Zdolność błędów $serii dowolnego$ kodu spełnia

Dowód

Najpierw zauważamy, że kod może poprawić wszystkie serie długości wtedy i tylko $nie$ różnią się sumą dwóch serii długości ${\ Displaystyle \ leqslant \ ell.}$$} \ Displaystyle \ mathbf {b} _ {1}}$ , że dwa słowa kodowe różnią się seriami ${\ Displaystyle \ mathbf {c} _ {1}}}$ i ${\ Displaystyle \ mathbf {c} _$ i ${\ Displaystyle \ mathbf {b} _ {2}}$ długości ${\ Displaystyle \ leqslant \ ell}$ każdy. Po otrzymaniu trafienia serią ${\ Displaystyle$$\ mathbf {b} _ {1}}$ zinterpretować to tak, jakby to było $displaystyle \mathbf {c} _ {2}}$ trafiony wybuchem ${\ Displaystyle - \ mathbf {b} _ {2}}$ . Nie możemy stwierdzić, czy przesłane słowo jest $}$$\ mathbf {c} _ {2}$ { . Załóżmy teraz, że każde dwa słowa kodowe różnią się o więcej niż dwa $serie$ . Nawet jeśli przesłane słowo kodowe zostanie trafione przez serię o długości $,$ nie będzie wyglądać jak inne słowo kodowe, które zostało trafione przez inne $\ displaystyle \ ell$ pękać. dla każdego słowa kodowego niech $c})}$$oznacza$ zestaw wszystkich słów, które różnią się od $}$${\ Displaystyle \ mathbf {c$ przez wybuch długości ${\ Displaystyle \ leqslant \ ell.}$${c})} .$ , że zawiera sam ${\ Displaystyle B (\ mathbf$ Z powyższej obserwacji wiemy, że dla dwóch różnych słów kodowych $\$$(\ mathbf {c} _ {i})}$ ) $_ {j},$ i ${\ Displaystyle B (\ mathbf {c} _ {j})}$ są rozłączne. Mamy słowa $_$ Dlatego możemy powiedzieć, że ${\ Displaystyle q ^ {k} | B (\ mathbf {c}) | \ leqslant q ^ {n}}$ . Ponadto mamy ${\ Displaystyle (n- \ ell) q ^ {\ ell -2} \ leqslant | B (\ mathbf {c}) |}$ . Podłączając drugą nierówność do pierwszej, a następnie biorąc logarytm podstawowy $.$ zmieniając układ, otrzymujemy powyższe twierdzenie

Silniejszy wynik daje granica Riegera:

Twierdzenie (związek Riegera) $Displaystyle 2\ell \leqslant nk}$$Jeśli$ jest zdolnością korygowania błędów serii $,$ blokowego .

Dowód

$jako$ może poprawić dowolny wzór serii o długości $mieć$ serii o długości słowa kodowego. Gdyby miał rozerwanie długości $kodowe$ , to rozerwanie długości mogłoby zmienić słowo kodowe na wzorzec rozerwania długości $ell }$$}$$\ displaystyle \$ , co również można uzyskać, popełniając błąd $serii o$ w całym zerowym słowie kodowym. Jeśli wektory są niezerowe w pierwszych $ℓ$ , to wektory powinny pochodzić z różnych podzbiorów tablicy, tak aby ich różnica nie była słowem kodowym serii o długości $Displaystyle 2 \ ell }$ . Spełniając ten warunek, liczba takich podzbiorów jest co najmniej równa liczbie wektorów. Zatem liczba podzbiorów wynosiłaby co najmniej ${\ displaystyle q ^ {2 \ ell}}$ . Stąd mamy co najmniej $symbole$ , w przeciwnym razie różnica dwóch takich wielomianów byłaby słowem kodowym będącym sumą dwóch serii o ${\ displaystyle \ leqslant \ ell.}$ Dowodzi to zatem związku Riegera.

Definicja. Liniowy kod korygujący błędy serii, osiągający powyższą granicę Riegera, nazywany jest optymalnym kodem korekcji błędów serii.

Dalsze ograniczenia korekcji błędów serii

Istnieje więcej niż jedna górna granica osiągalnej szybkości kodowania liniowych kodów blokowych dla wielofazowej korekcji serii (MPBC). Jedno takie ograniczenie jest ograniczone do maksymalnej możliwej do skorygowania długości impulsu cyklicznego w każdym podbloku lub równoważnie do ograniczenia minimalnej wolnej od błędów długości lub przerwy w każdym impulsie fazowym. To ograniczenie, zredukowane do szczególnego przypadku ograniczenia dla pojedynczej korekcji serii, jest wiązaniem Abramsona (następstwem wiązania Hamminga dla korekcji błędów serii), gdy cykliczna długość serii jest mniejsza niż połowa długości bloku.

Twierdzenie (liczba wybuchów) - dla binarnego ${\ Displaystyle 1 \ leqslant \ ell \ leqslant {\ tfrac {1} {2}} (n + 1)$ } alfabetu, istnieją wektory długości $^ {\ ell -1} + 1},$$które$ są seriami długości ${\ Displaystyle \ leqslant \ ell}$ .

Dowód

Ponieważ długość serii wynosi ${\ Displaystyle \ leqslant {\ tfrac {1} {2}} (n + 1)},$ istnieje unikalny opis serii związany z serią. Wybuch może rozpocząć się w dowolnej $pozycji$ . Każdy wzór zaczyna się od ${\ displaystyle 1}$ i zawiera długość ${\ displaystyle \ ell}$ . Możemy myśleć o tym jako o zbiorze wszystkich ciągów, które zaczynają się od $displaystyle$ mają długość $\ ell}$ . Tak więc w sumie możliwych jest $-1}}$ łącznie wybuchów ${ \ Displaystyle 2$ długość $\ Displaystyle \ leqslant \ ell.}$$wybuch$ całkowicie zerowy, mamy długości ${\ Displaystyle \ leqslant \ ell.}$

Twierdzenie (związane z liczbą słów kodowych) - Jeśli ${\ Displaystyle 1 \ leqslant \ ell \ leqslant {\ tfrac {1} {2}} (n + 1)}$ binarny ${\ Displaystyle \ ell}$ -burst kod korygujący błąd ma co najwyżej ${\ Displaystyle 2 ^ {n} / (n2 ^ {\ ell -1} + 1) }$ słowa kodowe.

Dowód

Ponieważ $+$ istnieje $_ ^ {\ ell -1} +1}$ wybuchy długości ${\ Displaystyle \ leqslant \ ell}$ . Powiedzmy $\ leqslant \ell }$ że kod ma słowa $kodowe$ , to są słowa kodowe, które różnią się od słowa kodowego serią długości $displaystyle \ \$ . Każde ze $słów musi$$być$ przeciwnym razie kod miałby . Dlatego ${\ Displaystyle M (2 ^ {\ ell -1} + 1) \ leqslant 2 ^ {n}}$ implikuje ${\ Displaystyle M \ leqslant 2 ^ {n} / (n2 ^ {\ ell -1} + 1).}$

Twierdzenie (granice Abramsona) - Jeśli jest binarną liniową ( ${\ Displaystyle (n, k), \ ell}$$ell \ leqslant {\ tfrac {1} {2}} (n + 1)}$ -burst kod korygujący błąd, jego długość bloku musi spełniać:

$${\ Displaystyle n \ leqslant 2 ^ {nk- \ ell + 1} -1.}$$

Dowód

Dla $kodu$ _ $_$ _ Wiemy to po naszym poprzednim wyniku

$${\ Displaystyle 2 ^ {k} \ leqslant {\ Frac {2 ^ {n}} {n2 ^ {\ ell -1} + 1}}.}$$

Izolując $+ 1}$$^ {- \ ell + 1}}$ 1 {\ Displaystyle n . Ponieważ i musi $liczbą$ całkowitą, mamy $nk-$$n \ leqslant 2$ .

Uwaga. ${\ Displaystyle r = nk}$ nazywa się redundancją kodu, aw alternatywnym sformułowaniu granic Abramsona jest ${\ displaystyle r \geqslant \lceil \log _{2}(n+1)\rceil +\ell -1.}$

Kody przeciwpożarowe

Chociaż ogólnie kody cykliczne są potężnymi narzędziami do wykrywania błędów serii, teraz rozważymy rodzinę binarnych kodów cyklicznych o nazwie Fire Codes, które mają dobre możliwości korekcji błędów pojedynczej serii. Przez pojedynczą serię, powiedzmy o długości $rozumiemy$ , że wszystkie błędy, które posiada odebrane słowo kodowe, mieszczą się w ustalonym $zakresie$ .

Niech ${\ Displaystyle p (x)}$ będzie nieredukowalnym wielomianem stopnia nad i $) {\$$Displaystyle \ mathbb {F} _ {2}}}$ i niech $\ displaystyle p}$ być okresem ${\ Displaystyle p (x)}$ . Okres $,$${\ Displaystyle p (x) | x ^ {r} -1.}$$zdefiniowany$ najmniej dodatnia liczba całkowita że $Displaystyle$ będzie dodatnią liczbą całkowitą spełniającą $\ ell \ leqslant m}$ i $-1}$$p (x)$ nie podzielne przez , gdzie $jest$ okresem $Displaystyle$ . Zdefiniuj kod przeciwpożarowy za pomocą następującego wielomianu generatora : ${\ displaystyle G}$

$${\ Displaystyle g (x) = \ lewo (x ^ {2 \ ell -1} + 1 \ prawo) p (x).}$$

Pokażemy, $że$$kodem$ korygującym błędy

Lemat 1 - ${\ Displaystyle \ gcd \ lewo (p (x), x ^ {2 \ ell -1} + 1 \ prawo) = 1 .}$

Dowód

Niech $dzielnikiem$ dwóch wielomianów Ponieważ ${\ Displaystyle p (x)}$ jest nieredukowalny, ${\ Displaystyle \ deg (d (x)) = 0}$ lub ${\ styl wyświetlania \deg(p(x))}$ . Załóżmy ${\ Displaystyle \ stopni (d (x)} \ neq 0,}$ wtedy $\ Displaystyle p (x) = cd (x) }$ dla pewnej stałej ${\ displaystyle c}$ . Ale ${\ Displaystyle (1/c) p (x)}$ jest dzielnikiem ${\ Displaystyle x ^ {2 \ ell -1} + 1}$ ponieważ ${\ Displaystyle d (x)}$ jest dzielnikiem ${\ Displaystyle x ^ {2 \ ell -1} + 1}$ . Jest to jednak sprzeczne z naszym założeniem, że ${\ Displaystyle p (x)}$ nie dzieli ${\ Displaystyle x ^ {2 \ ell -1} + 1.}$ Zatem ${\ Displaystyle \ stopień (d (x)) = 0,}$ udowadniając lemat.

Lemat 2 - Jeśli jest wielomianem okresu $\ Displaystyle p$$(x)}$${\ Displaystyle p (x) | x ^ {k} -1}$ wtedy i tylko wtedy, gdy ${\ displaystyle p | k.}$

Dowód

Jeśli ${\ Displaystyle p | k}$ , wtedy ${\ Displaystyle x ^ {k} -1 = ( x^{p}-1)(1+x^{p}+x^{2p}+\kropki +x^{k/p})}$ . Zatem ${\ Displaystyle p (x) | x ^ {k} -1.}$

Załóżmy teraz, że ${\ displaystyle p (x) | x ^ {k} -1}$ . Następnie ${\ Displaystyle k \ geqslant p}$ . Pokazujemy, że $k}$$displaystyle$ jest podzielna przez indukcję na $\ displaystyle k}$ . Następuje przypadek podstawowy ${\ displaystyle k = p}$ . Dlatego załóżmy, że ${\ displaystyle k> p}$ . Wiemy, że ${\ Displaystyle p ($ oba (ponieważ ma kropkę $x )$ }

$${\ Displaystyle x ^ {p} -1 = (x-1) \ lewo (1 + x + \ kropki + x ^ {p-1} \ prawo) \ quad {\ tekst {i}} \ quad x ^ {k }-1=(x-1)\lewo(1+x+\kropki +x^{k-1}\prawo).}$$

Ale ${\ Displaystyle p (x)}$ jest nieredukowalny, dlatego musi dzielić oba ${\ Displaystyle (1 + x + \ kropki + x ^ {p-1} )}$ i ${\ Displaystyle (1 + x + \ kropki + x ^ {k-1})}$ ; w ten sposób dzieli również różnicę dwóch ostatnich wielomianów, ${\ Displaystyle x ^ {p} (1 + x + \ kropki + x ^ {pk-1 })}$ . Wynika z tego, że ${\ Displaystyle p (x)}$ dzieli ${\ Displaystyle (1 + x + \ cdots + x ^ {pk-1}) }$ . Wreszcie dzieli również: ${\ Displaystyle x ^ {kp} -1 = (x-1) (1 +x+\kropki +x^{pk-1})}$ . Zgodnie z hipotezą indukcyjną, ${\ displaystyle p | kp}$ , a następnie ${\ displaystyle p | k}$ .

Konsekwencją lematu 2 jest to, że ponieważ ${\ Displaystyle p (x) = x ^ {p} -1}$ ma okres ${\ displaystyle p}$ , to ${\ displaystyle p (x)}$ dzieli ${\ Displaystyle x ^ {k} -1}$ wtedy i tylko wtedy, gdy ${\ displaystyle p | k}$ .

Twierdzenie - Kod przeciwpożarowy to $-burst$ błędów

Jeśli możemy pokazać, że wszystkie wybuchy o długości $mniejszej$ występują w różnych zestawach , możemy użyć ich jako liderów zestawu , które tworzą możliwe do skorygowania wzorce błędów. Powód jest prosty: wiemy, że z każdym cosetem związany jest unikalny syndrom dekodowania , a jeśli wszystkie impulsy o różnej długości występują w różnych cosetach, to wszystkie mają unikalne syndromy, ułatwiające korekcję błędów.

Dowód twierdzenia

Niech ${\ Displaystyle x ^ {i} a (x)}$ i ${\ Displaystyle x ^ {j} b (x)}$ będą wielomianami o stopniach ${\ displaystyle \ ell _ {1} -1}$ i ${\ Displaystyle \ ell _ {2} -1}$ , reprezentujące serie długości i ${\ Displaystyle \ ell _ {1}}$ i ${\ Displaystyle \ell _{2}}$ odpowiednio z ${\ Displaystyle \ ell _ {1}, \ ell _ {2} \ leqslant \ ell.}$ Liczby całkowite ${\ Displaystyle i, j}$ reprezentują pozycje początkowe impulsów i są mniejsze niż długość bloku kod. Ze względu na sprzeczność załóżmy, że $} a (x$ ja $x$ ) . Wtedy ${\ Displaystyle v (x) = x ^ {i} a (x) + x ^ {j} b (x)} jest$ a ważne słowo kodowe (ponieważ oba terminy znajdują się w tym samym zestawie). Bez utraty ogólności wybierz ${\ Displaystyle i \ leqslant j}$ . Z twierdzenia o dzieleniu możemy napisać: ${\ Displaystyle ji = g (2 \ ell -1) + r,}$ dla $całkowitych$ i ${\ Displaystyle r, 0 \ leqslant r <2 \ ell -1}$ . Przepisujemy wielomian w następujący sposób: ${\ displaystyle v (x)}$

$${\ Displaystyle v (x) = x ^{i}a(x)+x^{i+g(2\ell -1)+r}=x^{i}a(x)+x^{i+g(2\ell -1)+ r}+2x^{i+r}b(x)=x^{i}\left(a(x)+x^{b}b(x)\right)+x^{i+r}b( x)\left(x^{g(2\ell -1)}+1\right)}$$

Zauważ, że przy drugiej manipulacji wprowadziliśmy termin ${\ Displaystyle 2x ^ {i + r} b (x)}$ . Możemy to zrobić, ponieważ kody przeciwpożarowe działają na ${\ displaystyle \ mathbb {F} _ {2}}$ . Przy naszym założeniu, $x)}$ kodowym , a zatem $x$ być wielokrotnością $\ styl wyświetlania x^{2\ell -1}+1}$ ponieważ czynniki są względnie pierwsze, $Displaystyle v (x)}$$\$ muszą być podzielne przez . Przyglądając się uważnie ostatniemu wyrażeniu wyprowadzonemu dla $zauważamy$ , że ${\ Displaystyle x ^ {g (2 \ ell -1$ jest podzielna przez ${\ Displaystyle x ^ {2 \ ell -1} + 1}$ (zgodnie z Lematem 2). Dlatego ${\ Displaystyle a (x) + x ^ {b} b (x)}$ jest albo podzielne przez ${\ Displaystyle x ^ {2 \ ell -1} +1}$ lub jest ${\ Displaystyle 0}$ . Stosując ponownie twierdzenie o dzieleniu, widzimy, że istnieje wielomian $d (x)}$ takim stopniu, że : $Displaystyle$

$${\ Displaystyle a (x) + x ^ {b} b (x) = d (x) (x ^ {2\ell -1}+1)}$$

Wtedy możemy napisać:

$${\ Displaystyle {\ rozpocząć {wyrównane} \ delta + 2 \ ell -1 & = \ stopień \ lewo (d (x)\left(x^{2\ell -1}+1\right)\right)\\&=\deg \left(a(x)+x^{b}b(x)\right)\ \&=\deg \left(x^{b}b(x)\right)&&\deg(a(x))=\ell _{1}-1<2\ell -1\\&=b+\ ell _{2}-1\koniec{wyrównany}}}$$

Zrównując stopień obu boków, otrzymujemy ${\ Displaystyle b = 2 \ ell - \ ell _ {2} + \ delta.}$ Ponieważ ${\ Displaystyle \ ell _ {1}, \ ell _ {2} \ leqslant \ ell}$ my ${\ Displaystyle b \ geqslant \ ell + \ delta},$ ⩾ co implikuje $\ Displaystyle b> \ ell -1}$ i ${\ Displaystyle b> \ delta}$ . Zauważ, że w rozwinięciu:

$${\ Displaystyle a (x) + x ^ {b} b (x) = 1 + a_ {1} x + a_ {2} x ^ {2} + \ kropki + x ^ {\ ell _ {1} -1 }+x^{b}\left(1+b_{1}x+b_{2}x^{2}+\kropki +x^{\ell _{2}-1}\right).}$$

Termin pojawia $2$${\ Displaystyle \ delta <b <2 \ ell -1}$ ponieważ , wynikowe ${\ Displaystyle d (x) (x ^ {2 \ ell -1} + 1)}$ nie zawiera ${\ Displaystyle x ^ {b}}$ , więc ${\ displaystyle d (x) = 0}$ , a następnie ${\ Displaystyle a (x) + x ^ {b} b (x) = 0.}$ Wymaga to ${\ Displaystyle b = 0}$ i ${\ Displaystyle a (x) = b (x)}$ . Możemy dalej zrewidować nasz podział przez $\$$Displaystyle g (2 \ ell -1)},$ odzwierciedlić $= 0,}$ znaczy ${\ Displaystyle ji = g (2 \ ell -1)}$ . Podstawienie z powrotem do daje nam ${\ Displaystyle v (x)}$

$${\ Displaystyle v (x) = x ^ {i} b (x) \ lewo (x ^ {j-1} + 1 \ prawo).}$$

Ponieważ ${\ Displaystyle \ deg (b (x)) = \ ell _ {2} -1 <\ ell}$ , mamy ${\ Displaystyle \ stopień (b (x)) <\ stopień (p (x)) = m}$ . Ale $p (x)}$$}$ { \ $)$ muszą być względnie pierwsze. Ponieważ jest słowem kodowym, musi być podzielne przez ${\ Displaystyle p (x )$$)}$$^ {j-1} + 1$$x$ , ponieważ nie może być podzielna przez ${\ Displaystyle x ^ {2 \ ell -1} + 1}$ . Dlatego $ji}$ być wielokrotnością ${\ displaystyle$ . Ale musi to być również wielokrotność ${\ Displaystyle 2 \ ell -1}$ , co oznacza, że ​​musi to być wielokrotność ${\ Displaystyle n = {\ tekst { lcm}}(2\ell -1,p)}$ ale jest to dokładnie długość bloku kodu. Dlatego $\$ być wielokrotnością $displaystyle n},$ ponieważ oba są mniejsze niż $displaystyle n}$ . Zatem nasze założenie, że $a$$(x)}$ \ i $zestawach , z$ zespołami, a zatem możliwe do naprawienia.

Przykład: 5-burst error poprawiający kod pożaru

Korzystając z teorii przedstawionej w powyższej sekcji, rozważ konstrukcję kodu przeciwpożarowego korygującego błąd ${\ displaystyle 5} . Pamiętaj$$,$ że aby skonstruować kod przeciwpożarowy, potrzebujemy nieredukowalnego wielomianu $,$ całkowitej musimy $}$ właściwość, że podzielna przez okres $\ Displaystyle 2 \ ell -1$ { $_$ na i ${\ Displaystyle \ ell = 5}$ . Ponieważ $prymitywnym wielomianem$ , jego okres wynosi $\ Displaystyle 2 ^ {5} -1 =$ . Potwierdzamy, że $Displaystyle$ jest podzielna przez $2 \ ell -1 = 9}$ . Zatem,

$${\ Displaystyle g (x) = (x ^ {9 }+1)\left(1+x^{2}+x^{5}\right)=1+x^{2}+x^{5}+x^{9}+x^{11}+ x^{14}}$$

jest generatorem kodów pożarowych. Możemy obliczyć długość bloku kodu, oceniając najmniejszą wspólną wielokrotność $displaystyle$ 2 $2 \ ell -1}$ . Innymi słowy, ${\ Displaystyle n = {\ tekst {lcm}} (9,31) = 279}$ . Zatem powyższy $lub$ ogniowy jest kodem cyklicznym zdolnym do korygowania dowolnego wybuchu o długości mniejszej.

Binarne kody Reeda-Solomona

Niektóre rodziny kodów, takie jak Reed-Solomon , działają na rozmiarach alfabetu większych niż binarne. Ta właściwość przyznaje takim kodom potężne możliwości korekcji błędów serii. Rozważ kod działający na ${\ displaystyle \ mathbb {F} _ {2 ^ {m}}}$ . Każdy symbol alfabetu może być reprezentowany $przez$ . Jeśli jest to kod Reeda-Solomona na $\ mathbb {F} _ {2 ^ {m}}} , do ($${\ Displaystyle$$n$ } $mn, mk] _$ myśleć o ${2}}$ nad kodem do $Displaystyle$ [

Powodem, dla którego takie kody są skuteczne w korekcji błędów serii, jest to, że każdy symbol jest reprezentowany przez $ogólnie$$i$ ma znaczenia, ile z tych bitów jest błędnych; niezależnie od tego $, czy$ bit, czy wszystkie bity zawierają błędy, z perspektywy dekodowania jest to nadal błąd pojedynczego symbolu. Innymi słowy, ponieważ błędy seryjne zwykle występują w klastrach, istnieje duże prawdopodobieństwo, że kilka błędów binarnych przyczyni się do błędu pojedynczego symbolu.

Zauważ, że seria błędów może mieć wpływ co najwyżej na $+ 1} może$${$ m $2m$ na większość symboli ${\ displaystyle 3}$ . $_$ wybuch $na$ co _ oznacza to, że $symboli$ może co najwyżej poprawić serię długości $\ displaystyle (t-1) m + 1}$ .

Ogólnie rzecz biorąc, $}$$displaystyle t$ -Solomona w ciągu poprawić dowolną kombinację t

$${\ Displaystyle {\ Frac {t} {1 + \ lfloor (l + m-2) / m \ rfloor}}}$$

$mniej$ wybuchów o długości $.$ oprócz możliwości korygowania przypadkowych błędów w najgorszym przypadku

Przykład binarnego kodu RS

Niech $będzie$ za ${\ Displaystyle [255,223,33]}$ RS code over $\ Displaystyle \ mathbb {F} _ {2 ^ {8}}}$ . Kod ten został zastosowany przez NASA w ich statku kosmicznym Cassini-Huygens . Jest $_$ _ Teraz konstruujemy Binarny kod RS z $G'}$$displaystyle$ . Każdy symbol zostanie zapisany przy użyciu bitów ${\ Displaystyle \ lceil \ log _ {2} (255) \ rceil = 8}$ Dlatego binarny kod RS będzie miał parametry jako ${\ displaystyle [2040,1784,33] _ {2}} .$ Jest w stanie skorygować każdą pojedynczą serię o długości ${\ displaystyle l = 121}$ .

Kody przeplatane

Przeplot służy do konwersji kodów splotowych z losowych korektorów błędów na korektory błędów serii. Podstawową ideą stosowania kodów z przeplotem jest pomieszanie symboli w nadajniku. Prowadzi to do randomizacji serii odebranych błędów, które są blisko siebie i możemy następnie zastosować analizę dla losowego kanału. Zatem główną funkcją wykonywaną przez element przeplotu w nadajniku jest zmiana wejściowej sekwencji symboli. W odbiorniku element rozplatający zmieni odebraną sekwencję, aby odzyskać pierwotną niezmienioną sekwencję w nadajniku.

Wydajność korygowania błędów serii przeplotu

Ilustracja kolejności głównych wierszy i kolumn

Twierdzenie - Jeśli zdolność korygowania błędów serii jakiegoś kodu wynosi ${\ Displaystyle \ lambda \ ell.}$$\ ell,},$$displaystyle$ to zdolność korygowania błędów serii jego -way przeplotu wynosi

Dowód

$,$ że mamy kod ${\ Displaystyle \ leqslant \ ell.}$ serie Przeplot może dostarczyć nam kodu, który może poprawić wszystkie serie długości $\ leqslant \ lambda \ ell,}$$(\ lambda n, \ lambda k$$Displaystyle$ dla dowolnego danego ${\ displaystyle \ lambda}$ . Jeśli chcemy zakodować wiadomość o dowolnej długości za pomocą przeplotu, najpierw dzielimy ją na bloki o długości ${\ displaystyle \ lambda k}$ . $Wpisy$ każdego bloku w $użyciu$ głównych Następnie kodujemy każdy wiersz za pomocą kodu ${\ displaystyle (n, k)}$ . Otrzymamy macierz ${\ displaystyle \ lambda \ razy n}$ . Teraz ta macierz jest odczytywana i przesyłana w kolejności kolumnowej. $, że jeśli$ w przesłanym słowie wystąpi seria długości, to każdy wiersz będzie zawierał w kolejne $($ dokładniej ⌊ ${\ Displaystyle \ lfloor {\ tfrac {h} {\ lambda}} \ rfloor}$ i co najwyżej $\ Displaystyle \ lceil {\ tfrac { h}{\lambda}}\rceil}$ ). h ${\ Displaystyle h \ leqslant \ lambda \ ell,}$ to $Displaystyle {\ tfrac {h} {\ lambda}} \ leqslant \ ell}$ i ${ \displaystyle (n,k)}$ może poprawić każdy wiersz. Dlatego kod $_$$_$ _ I odwrotnie, jeśli $> \ lambda \ ell,}$$Displaystyle$ to co najmniej jeden wiersz będzie zawierał więcej niż błędy, a ${\ displaystyle (n, k)}$ kod może ich nie poprawić. Dlatego $}$ korygowania błędów przeplatanego kodu wynosi dokładnie $\ Displaystyle (\ lambda n, \ lambda k)$$lambda \ ell$ Wydajność BEC kodu z przeplotem pozostaje taka sama jak . To prawda, ponieważ:

$${\ Displaystyle {\ Frac {2 \ lambda \ ell}} {\ lambda n- \ lambda k}} = {\ Frac {2 \ ell} {nk}} }$$

Blok przeplotu

Poniższy rysunek przedstawia układ przeplotu 4 na 3.

Przykład przeplotu bloków

Powyższy układ przeplotu nazywany jest układem przeplotu blokowego . Tutaj symbole wejściowe są zapisywane sekwencyjnie w wierszach, a symbole wyjściowe są uzyskiwane przez sekwencyjne odczytywanie kolumn. Zatem ma to postać tablicy ${\ displaystyle M \ razy N}$ . $biorąc$ , to długość słowa kodowego.

Pojemność elementu przeplatającego bloki : dla elementu $serii$ długości $ell}$${\ displaystyle {\ tfrac {\ ell} {M}}.}$ górna granica liczby błędów Jest to oczywiste z faktu, że czytamy mądrze kolumnę wyjściową, a liczba wierszy to ${\ displaystyle M}$ . Zgodnie z powyższym twierdzeniem dotyczącym zdolności korekcji błędów do $wynosi$ dozwolonej długości ${\ Displaystyle Mt.}$ Dla długości serii ${\ Displaystyle Mt + 1}$ dekoder może zawieść.

Wydajność elementu przeplatającego bloki ( $:$ Można ją znaleźć, biorąc stosunek długości serii, w której dekoder może zawieść do pamięci elementu przeplatającego. W ten sposób możemy sformułować jako ${\ displaystyle \ gamma}$

$${\ Displaystyle \ gamma = {\ Frac {Mt + 1} {MN}} \ około {\ Frac {t} {N}}.}$$

Wady mechanizmu przeplotu bloków: Jak wynika z rysunku, kolumny są odczytywane sekwencyjnie, odbiorca może zinterpretować pojedynczy wiersz dopiero po odebraniu całej wiadomości, a nie wcześniej. Ponadto odbiornik wymaga znacznej ilości pamięci w celu przechowywania odebranych symboli i musi przechowywać całą wiadomość. Zatem czynniki te powodują dwie wady, jedną jest opóźnienie, a drugą jest pamięć (dość duża ilość pamięci). Tych wad można uniknąć, stosując splotowy element przeplatający opisany poniżej.

Przeplot splotowy

Cross Interleaver jest rodzajem systemu multipleksera-demultipleksera. W tym systemie linie opóźniające służą do stopniowego zwiększania długości. Linia opóźniająca jest w zasadzie obwodem elektronicznym służącym do opóźnienia sygnału o określony czas. Niech ${\ displaystyle n}$ będzie liczbą linii opóźniających i $będzie$ liczbą symboli wprowadzonych przez każdą linię opóźniającą Zatem separacja między kolejnymi symbolami wejść = ${\ displaystyle nd}$ . Niech długość słowa kodowego ${\ displaystyle \ leqslant n.}$ Zatem każdy symbol w wejściowym słowie kodowym będzie znajdować się na odrębnej linii opóźniającej. Niech wystąpi błąd serii o długości ${\ displaystyle \ ell}$ . Ponieważ separacja między kolejnymi symbolami wynosi ${\ displaystyle nd,}$ liczba błędów, które może zawierać przepleciony wynik, wynosi ${\ Displaystyle {\ tfrac {\ ell} {nd + 1}}.} Zgodnie z$$powyższym$ twierdzeniem, dla zdolności korekcji błędów do maksymalna dozwolona długość serii to ${\ Displaystyle (nd + 1) (t-1).}$ Dla długości serii ${\ Displaystyle (nd + 1) (t-1) + 1,}$ dekoder może ulec awarii.

Przykład splotowego elementu przeplotowego

Przykład narzędzia do usuwania przeplotu

Wydajność elementu przeplatającego krzyżowo ( $:$ Można ją znaleźć, biorąc stosunek długości serii, w której dekoder może zawieść, do pamięci elementu przeplatającego. W takim przypadku pamięć układu przeplotu można obliczyć jako

$${\ Displaystyle (0 + 1 + 2 + 3 + \ cdots + (n-1)) d = {\ Frac {n (n-1)} {2}} re.}$$

Zatem możemy sformułować w następujący sposób: ${\ displaystyle \ gamma}$

$${\ Displaystyle \ gamma = {\ Frac {(nd + 1) (t-1) + 1} {{\ Frac {n (n-1)} {2}} d}}.}$$

Wydajność układu przeplotu krzyżowego: Jak pokazano na powyższym rysunku układu przeplotu, dane wyjściowe to nic innego jak ukośne symbole generowane na końcu każdej linii opóźniającej. W tym przypadku, gdy przełącznik multipleksera wejściowego zakończy około połowy przełączania, możemy odczytać pierwszy wiersz w odbiorniku. W związku z tym musimy przechowywać maksymalnie około połowy wiadomości u odbiorcy, aby przeczytać pierwszy wiersz. To drastycznie zmniejsza zapotrzebowanie na pamięć o połowę. Ponieważ do odczytania pierwszego wiersza wymagana jest teraz tylko połowa wiadomości, opóźnienie jest również zmniejszone o połowę, co jest dobrą poprawą w stosunku do mechanizmu przeplotu bloków. W ten sposób cała pamięć układu przeplotu jest dzielona między nadajnik i odbiornik.

Aplikacje

Płyta CD

Bez kodów korekcji błędów dźwięk cyfrowy nie byłby technicznie wykonalny. Kody Reeda -Solomona mogą poprawić uszkodzony symbol z błędem pojedynczego bitu tak samo łatwo, jak mogą poprawić symbol z błędnymi wszystkimi bitami. To sprawia, że ​​kody RS są szczególnie odpowiednie do korygowania błędów serii. Zdecydowanie najpowszechniejszym zastosowaniem kodów RS są płyty kompaktowe. Oprócz podstawowej korekcji błędów zapewnianej przez kody RS, ochronę przed błędami serii wynikającymi z zadrapań na dysku zapewnia układ przeplotu krzyżowego.

Obecny cyfrowy system audio na płytach kompaktowych został opracowany przez NV Philips z Holandii i Sony Corporation z Japonii (umowa podpisana w 1979 r.).

Płyta kompaktowa zawiera aluminiowaną płytę o średnicy 120 mm pokrytą przezroczystą powłoką z tworzywa sztucznego, ze spiralną ścieżką o długości około 5 km, która jest skanowana optycznie za pomocą lasera o długości fali ~0,8 μm, ze stałą prędkością ~1,25 m/s. Aby osiągnąć tę stałą prędkość, obroty dysku zmieniają się od ~ 8 obr./s podczas skanowania wewnętrznej części toru do ~ 3,5 obr./s w części zewnętrznej. Wgłębienia i ziemie to zagłębienia (głębokość 0,12 μm) oraz płaskie segmenty stanowiące dane binarne wzdłuż toru (szerokość 0,6 μm).

Proces CD można wyabstrahować jako sekwencję następujących podprocesów:

• Kodowanie kanałów źródła sygnałów
• Mechaniczne podprocesy przygotowania płyty wzorcowej, tworzenia płyt użytkownika i wykrywania sygnałów osadzonych na płytach użytkownika podczas odtwarzania – kanał
• Dekodowanie sygnałów wykrytych z płyt użytkownika

Proces podlega zarówno błędom serii, jak i przypadkowym błędom. Błędy związane z rozerwaniem obejmują błędy związane z materiałem dysku (wady odblaskowej folii aluminiowej, słaby współczynnik odbicia przezroczystego materiału dysku), produkcją dysku (błędy podczas formowania dysku i cięcia dysku itp.), obchodzeniem się z dyskiem (zadrapania – zazwyczaj cienkie, promieniowe i prostopadłe do kierunek nagrywania) i różnice w mechanizmie odtwarzania. Błędy losowe obejmują te spowodowane jitterem zrekonstruowanej fali sygnału oraz zakłóceniami w sygnale. CIRC ( ang. Cross-Interleaved Reed–Solomon code ) jest podstawą wykrywania i korygowania błędów w procesie CD. Koryguje serie błędów do 3500 bitów w sekwencji (długość 2,4 mm, jak widać na powierzchni płyty CD) i kompensuje serie błędów do 12 000 bitów (8,5 mm), które mogą być spowodowane drobnymi zarysowaniami.

Kodowanie: Fale dźwiękowe są próbkowane i konwertowane do postaci cyfrowej przez przetwornik A/D. Fala dźwiękowa jest próbkowana pod kątem amplitudy (przy 44,1 kHz lub 44 100 parach, po jednej dla lewego i prawego kanału dźwięku stereo). Amplituda w instancji jest przypisywana do ciągu binarnego o długości 16. Zatem każda próbka wytwarza dwa wektory binarne z lub 4 $} displaystyle \mathbb {F} _{2}^{8}}$${\ Displaystyle \ mathbb {F} _$ bajtów danych. Każda sekunda zarejestrowanego dźwięku to 44 100 × 32 = 1 411 200 bitów (176 400 bajtów) danych. Próbkowany strumień danych o szybkości 1,41 Mbit/s przechodzi przez system korekcji błędów i ostatecznie zostaje przekształcony w strumień o szybkości 1,88 Mbit/s.

Wejście dla enkodera składa się z ramek wejściowych, z których każda zawiera 24 8-bitowe symbole (12 16-bitowych próbek z przetwornika A/D, po 6 z lewego i prawego źródła danych (dźwięku). Ramkę można przedstawić za pomocą ${\ Displaystyle L_ {1} R_ {1} L_ {2} R_ {2} \ ldots L_ {6} R_ {6}$ } $L_ {i}$${ \$$}$ i są z lewego i prawego kanału ramki

Początkowo bajty są permutowane w celu utworzenia nowych ramek reprezentowanych przez ${\ Displaystyle L_ {1} L_ {3} L_ {5 } R_ {1} R_ {3} R_ {5} L_ {2} L_ {4} L_ {6} R_ {2} R_ {4} R_ {6}}$ gdzie ${\ Displaystyle L_ {i }, R_ {i}}$ reprezentują $lewą$ i prawą próbkę z klatki po 2 interweniujących klatkach.

Następnie te 24 symbole wiadomości są kodowane przy użyciu kodu C2 (28,24,5) Reeda-Solomona, który jest skróconym kodem RS na ${\ displaystyle \ mathbb {F} _ {256}}$ . Jest to korekcja dwóch błędów, mająca minimalną odległość 5. Dodaje to 4 bajty nadmiarowości, ${\ Displaystyle L_ {1} L_ {3} L_ {5} R_ {1} R_ {3} R_ {5} P_ {1} }P_{2}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}}$ P ${1} P_ {2}$ . Otrzymane 28-symbolowe słowo kodowe jest przepuszczane przez (28,4) element przeplatający krzyżowo, co prowadzi do 28 przeplatanych symboli. Są one następnie przepuszczane przez kod RS C1 (32,28,5), w wyniku czego powstają słowa kodowe składające się z 32 zakodowanych symboli wyjściowych. Dalsze przegrupowywanie nieparzystych symboli słowa kodowego z parzystymi symbolami następnego słowa kodowego jest przeprowadzane w celu rozbicia wszelkich krótkich serii, które mogą nadal występować po powyższym 4-ramkowym przeplocie opóźniającym. Zatem na każde 24 symbole wejściowe będą 32 symbole wyjściowe, co daje ${\ displaystyle R = 24/32}$ . Na koniec dodawany jest jeden bajt informacji kontrolnych i wyświetlających. Każdy z 33 bajtów jest następnie konwertowany na 17 bitów poprzez EFM (modulacja od ośmiu do czternastu) i dodanie 3 bitów scalających. Dlatego ramka sześciu próbek daje w wyniku 33 bajty × 17 bitów (561 bitów), do których dodaje się 24 bity synchronizacji i 3 bity scalające, co daje łącznie 588 bitów.

Dekodowanie: Odtwarzacz CD (dekoder CIRC) odbiera 32 wyjściowy strumień danych symboli. Strumień ten przechodzi najpierw przez dekoder D1. Indywidualni projektanci systemów CD decydują o metodach dekodowania i optymalizacji wydajności swoich produktów. Mając minimalną odległość 5 Dekodery D1, D2 mogą korygować kombinację $\$ i $wymazań$ tak, że $displaystyle 2e + f <5$ . W większości rozwiązań dekodujących D1 jest przeznaczony do korygowania pojedynczego błędu. A w przypadku więcej niż 1 błędu ten dekoder wyprowadza 28 wymazań. Element usuwający przeplot na kolejnym etapie rozdziela te wymazywania na 28 słów kodowych D2. Ponownie w większości rozwiązań D2 ma zajmować się tylko wymazywaniem (prostsze i tańsze rozwiązanie). W przypadku wystąpienia więcej niż 4 wymazań, D2 wyprowadza 24 wymazań. Następnie system ukrywania błędów próbuje interpolować (z sąsiednich symboli) w przypadku niepoprawnych symboli, w przeciwnym razie dźwięki odpowiadające takim błędnym symbolom zostają wyciszone.

Wydajność CIRC: CIRC ukrywa błędy długich popiersi poprzez prostą interpolację liniową. 2,5 mm długości ścieżki (4000 bitów) to maksymalna całkowicie korygowana długość serii. Długość ścieżki 7,7 mm (12 300 bitów) to maksymalna długość serii, którą można interpolować. Częstotliwość interpolacji próbek to jedna na 10 godzin przy współczynniku błędów bitowych (BER) ${\ displaystyle = 10 ^ {-4}}$ i 1000 próbek na minutę przy BER = ${\ displaystyle 10 ^ {- 3} }$ Niewykrywalne próbki błędów (kliknięcia): mniej niż jedna na 750 godzin przy BER = ${\ Displaystyle 10 ^ {- 3}}$ i pomijalne przy BER = ${\ Displaystyle 10 ^ {- 4}}$ .

Zobacz też

• Wykrywanie i korygowanie błędów
• Kody korygujące błędy z informacją zwrotną
• Szybkość kodowania
• Korekcja błędów Reeda-Solomona