Wygładzanie jądra

Wygładzanie jądra to technika statystyczna $jako$ do oszacowania funkcji rzeczywistych ważonej sąsiednich zaobserwowanych Waga jest określana przez jądro , tak że bliższe punkty mają większą wagę. Oszacowana funkcja jest gładka, a poziom gładkości jest ustalany przez jeden parametr. Wygładzanie jądra jest rodzajem ważonej średniej kroczącej .

Definicje

Niech ${\ Displaystyle K_ {h_ {\ lambda}} (X_ {0}, X)}$ będzie jądrem zdefiniowanym przez

{\ Displaystyle K_ {h_ {\ lambda}} (X_ {0}, X) = D \ lewo ({\ Frac { \left\|X-X_{0}\right\|}{h_{\lambda }(X_{0})}}\right)}

Gdzie:

${\ Displaystyle X, X_ {0} \ w \ mathbb {R} ^ {p}}$
${\ Displaystyle \ lewo \|\ cdot \ prawo \|}$ jest normą euklidesową
${\ Displaystyle h _ {\ lambda} (X_ {0})}$ jest parametrem (promień jądra)
₀ D ( t ) jest zazwyczaj dodatnią funkcją o wartościach rzeczywistych, której wartość maleje (lub nie rośnie) wraz ze wzrostem odległości między X a X .

Popularne jądra używane do wygładzania obejmują jądra paraboliczne (Epanechnikov), Tricube i Gaussa .

Niech ${\ Displaystyle Y (X): \ mathbb {R} ^ {p} \ do \ mathbb {R}}$ będzie ciągłą funkcją X . Dla każdego średnia ważona jądrem Nadarayi-Watsona (gładkie oszacowanie Y ( X )) jest zdefiniowana przez ${\ Displaystyle X_ {0} \ in \ mathbb {R} ^ {p}}$

{\ Displaystyle {\ kapelusz {Y}} ( X_{0})={\frac {\sum \limits _{i=1}^{N}{K_{h_{\lambda}}(X_{0},X_{i})Y(X_{i} )}}{\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})}}}}

Gdzie:

N to liczba obserwowanych punktów
Y ( X _i ) to obserwacje w punktach X _i .

W poniższych sekcjach opisujemy niektóre szczególne przypadki wygładzania jądra.

Wygładzanie jądra Gaussa

Jądro Gaussa jest jednym z najczęściej używanych jąder i jest wyrażone za pomocą poniższego równania.

{\ Displaystyle K (x ^ {*}, x_ {i}) = \ exp \ lewo (- {\ frac {(x^{*}-x_{i})^{2}}{2b^{2}}}\right)}

Tutaj b jest skalą długości dla przestrzeni wejściowej.

Najbliższy sąsiad gładszy

₀₀ Idea wygładzania najbliższego sąsiada jest następująca. Dla każdego punktu X weź m najbliższych sąsiadów i oszacuj wartość Y ( X ) przez uśrednienie wartości tych sąsiadów.

Formalnie ${\ Displaystyle h_ {m} (X_ {0}) = \ lewo \| X_ {0} -X_ {[m]} \ prawo \ |}$ , gdzie jest m- tym najbliższym X sąsiadem i ${\ Displaystyle X_ {[m]}}$ ₀

{\ Displaystyle D (t) = {\ rozpocząć {przypadki} 1/m & {\ tekst {jeśli}} | t | \ równoważnik 1 \\ 0 & {\ tekst {w przeciwnym razie}} \ koniec {przypadków}}}

Przykład:

₀₀ W tym przykładzie X jest jednowymiarowe. Dla każdego X $.$ średnią 16 najbliższych X punktów (oznaczonych Wynik nie jest wystarczająco gładki.

Jądro średnio płynniejsze

₀₀₀ Idea przeciętnego wygładzenia jądra jest następująca. Dla każdego punktu danych X wybierz stały rozmiar odległości λ ( promień jądra lub szerokość okna dla p = 1 wymiar) $i$ oblicz średnią ważoną dla wszystkich punktów danych, które są bliżej niż ( bliżej X punktów uzyskują wyższe wagi).

Formalnie ${\ Displaystyle h _ {\ lambda} (X_ {0}) = \ lambda = {\ tekst {stała}},}$ i D ( t ) jest jednym z popularnych jąder .

Przykład:

₀₀₀ Dla każdego X szerokość okna jest stała, a waga każdego punktu w oknie jest schematycznie oznaczona żółtą cyfrą na wykresie. Można zauważyć, że estymacja jest gładka, ale punkty brzegowe są obciążone. Powodem tego jest nierówna liczba punktów (od prawej i od lewej do X ) w oknie, gdy X jest wystarczająco blisko granicy.

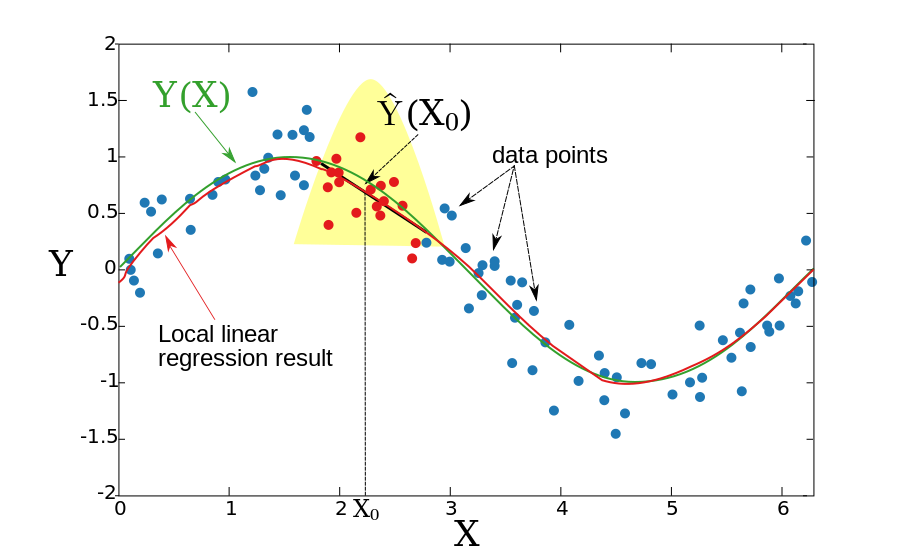
Lokalna regresja liniowa

₀₀ W dwóch poprzednich sekcjach założyliśmy, że podstawowa funkcja Y(X) jest lokalnie stała, dlatego mogliśmy użyć średniej ważonej do oszacowania. Ideą lokalnej regresji liniowej jest dopasowanie lokalnie linii prostej (lub hiperpłaszczyzny dla większych wymiarów), a nie stałej (linia pozioma). $zapewnione$ linii oszacowanie tej linii w X. Powtarzając tę procedurę dla każdego X , można otrzymać funkcję estymacji ${\ Displaystyle {\ kapelusz {Y}} (X)}$ . Podobnie jak w poprzedniej sekcji, szerokość okna jest stała ${\ Displaystyle h_ {\ lambda} (X_ {0}) = \ lambda = {\ tekst {stała}}.$ Formalnie lokalna regresja liniowa jest obliczana przez rozwiązanie ważonego problemu najmniejszych kwadratów.

Dla jednego wymiaru ( p = 1):

${\ Displaystyle {\ rozpocząć {wyrównane} & \ min _ {\ alfa (X_ {0}), \ beta (X_ {0})} \ suma \ limity _ {i = 1} ^{N}{K_{h_{\lambda}}(X_{0},X_{i})\left(Y(X_{i})-\alfa (X_{0})-\beta (X_{0 })X_{i}\right)^{2}}\\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\Strzałka w dół \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,{\kapelusz {Y}}(X_{0})=\alfa (X_{0})+\beta (X_{0} )X_{0}\\\koniec{wyrównany}}}$

Rozwiązanie w postaci zamkniętej jest podane przez:

{\ Displaystyle {\ kapelusz {Y}} (X_ {0}) = \ lewo (1 ,X_{0}\right)\left(B^{T}W(X_{0})B\right)^{-1}B^{T}W(X_{0})y}

Gdzie:

${\ Displaystyle y = \ lewo (Y (X_ {1}), \ kropki, Y (X_ {N}) \ prawo) ^ {T }}$
${\ Displaystyle W (X_ {0}) = \ operatorname {diag} \ lewo (K_ {h_ {\ lambda}} (X_ {0},X_{i})\prawo)_{N\razy N}}$
${\ Displaystyle B ^ {T} = \ lewo ({\ rozpocząć {macierz} 1 i 1 i \ kropki i 1 \\ X_ {1} i X_ {2} i \ kropki &X_{N}\\\koniec{macierzy}}\prawo)}$

Przykład:

Wynikowa funkcja jest gładka, a problem z obciążonymi punktami granicznymi jest zmniejszony.

Lokalną regresję liniową można zastosować do przestrzeni dowolnej wymiarowej, chociaż pytanie, czym jest lokalne sąsiedztwo, staje się bardziej skomplikowane. Często stosuje się k punktów treningowych najbliższych punktowi testowemu, aby dopasować lokalną regresję liniową. Może to prowadzić do dużej zmienności dopasowanej funkcji. Aby ograniczyć wariancję, zestaw punktów treningowych powinien zawierać punkt testowy w ich wypukłym kadłubie (patrz odnośnik Gupta i in.).

Lokalna regresja wielomianowa

Zamiast dopasowywać lokalnie funkcje liniowe, można dopasować funkcje wielomianowe.

Dla p=1 należy zminimalizować:

${\ Displaystyle {\ underset {\ alfa (X_ {0}), \ beta _ {j} (X_ {0}), j = 1, ..., d} {\ mathop {\min }}}\,\sum \limits_{i=1}^{N}{K_{h_{\lambda}}(X_{0},X_{i})\left(Y(X_{ i})-\alpha (X_{0})-\sum \limits _{j=1}^{d}{\beta _{j}(X_{0})X_{i}^{j}}\ dobrze)^{2}}}$

z ${\ Displaystyle {\ kapelusz {Y}} (X_ {0}) = \ alfa (X_ {0}) + \sum \limits _{j=1}^{d}{\beta _{j}(X_{0})X_{0}^{j}}}$

W przypadku ogólnym (p>1) należy minimalizować:

${\ Displaystyle {\ rozpocząć {wyrównane} i {\ kapelusz {\ beta}} (X_ {0}) = {\ underset {\ beta (X_ {0})} {\ mathop {\ arg \ min}}} \ ,\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-b(X_{ i})^{T}\beta (X_{0})\right)}^{2}\\&b(X)=\left({\begin{matrix}1,&X_{1},&X_{2} ,...&X_{1}^{2},&X_{2}^{2},...&X_{1}X_{2}\,\,\,...\\\koniec{macierzy}} \right)\\&{\kapelusz {Y}}(X_{0})=b(X_{0})^{T}{\kapelusz {\beta}}(X_{0})\\\koniec{ wyrównany}}}$

Zobacz też

Li, Q. i JS Racine. Ekonometria nieparametryczna: teoria i praktyka . Princeton University Press, 2007, ISBN 0-691-12161-3 .
T. Hastie, R. Tibshirani i J. Friedman, Elementy uczenia się statystycznego , rozdział 6, Springer, 2001. ISBN 0-387-95284-5 ( strona z książką towarzyszącą ).
M. Gupta, E. Garcia i E. Chin, „Adaptive Local Linear Regression with Application to Printer Color Management”, IEEE Trans. Przetwarzanie obrazu 2008.