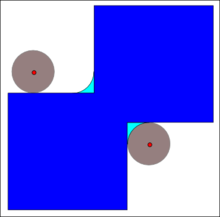
Zamknięcie (morfologia)

Zamknięcie ciemnoniebieskiego kształtu (połączenie dwóch kwadratów) krążkiem, co skutkuje połączeniem ciemnoniebieskiego kształtu i jasnoniebieskich obszarów.

W morfologii matematycznej zamknięcie zbioru ( obrazu binarnego ) A przez element konstruujący B jest erozją dylatacji tego zbioru ,

{\ Displaystyle A \ punktor B = (A \ oplus B) \ ominus B \,}

gdzie $}$ $oplus$ i oznaczają rozszerzenie i erozję.

W przetwarzaniu obrazu zamykanie jest, obok otwierania , podstawowym narzędziem usuwania szumu morfologicznego . Otwieranie usuwa małe przedmioty, a zamykanie usuwa małe dziury.

Nieruchomości

Jest idempotentny , to znaczy ${\ Displaystyle (A \ punktor B) \ punktor B = A \ punktor B}$ .
Rośnie , to znaczy, jeśli , to $Displaystyle$ $A \ punktor B \ subseteq C$ do }
Jest obszerny , tj. $\ Displaystyle A \ subseteq A \ punktor B}$ .
Jest niezmiennikiem translacji .

Zobacz też

Bibliografia

Analiza obrazu i morfologia matematyczna Jean Serra, ISBN 0-12-637240-3 (1982)
Analiza obrazu i morfologia matematyczna, tom 2: Postępy teoretyczne, Jean Serra, ISBN 0-12-637241-1 (1988)
Wprowadzenie do przetwarzania obrazu morfologicznego autorstwa Edwarda R. Dougherty'ego, ISBN 0-8194-0845-X (1992)

Linki zewnętrzne

Wprowadzenie do morfologii matematycznej