Algebra relacyjna

Nie mylić z algebrą relacji .

W teorii baz danych algebra relacyjna jest teorią, która wykorzystuje struktury algebraiczne do modelowania danych i definiowania na ich podstawie zapytań z dobrze ugruntowaną semantyką . Teoria została wprowadzona przez Edgara F. Codda .

Głównym zastosowaniem algebry relacyjnej jest zapewnienie teoretycznych podstaw relacyjnych baz danych , w szczególności języków zapytań dla takich baz danych, wśród których głównym jest SQL . Relacyjne bazy danych przechowują dane tabelaryczne reprezentowane jako relacje . Zapytania dotyczące relacyjnych baz danych również często zwracają dane tabelaryczne reprezentowane jako relacje .

Głównym celem algebry relacyjnej jest zdefiniowanie operatorów, które przekształcają jedną lub więcej relacji wejściowych w relację wyjściową. Biorąc pod uwagę, że operatory te akceptują relacje jako dane wejściowe i tworzą relacje jako dane wyjściowe, można je łączyć i wykorzystywać do wyrażania potencjalnie złożonych zapytań, które przekształcają potencjalnie wiele relacji wejściowych (których dane są przechowywane w bazie danych) w pojedynczą relację wyjściową (wyniki zapytania) .

Operatory jednoargumentowe akceptują jako dane wejściowe pojedynczą relację; przykłady obejmują operatory filtrujące określone atrybuty (kolumny) lub krotki (wiersze) z relacji wejściowej.

Operatory binarne akceptują jako dane wejściowe dwie relacje; takie operatory łączą dwie relacje wejściowe w jedną relację wyjściową, na przykład biorąc wszystkie krotki znalezione w jednej relacji, usuwając krotki z pierwszej relacji znalezionej w drugiej relacji, rozszerzając krotki pierwszej relacji o krotki drugiej relacji spełnienia określonych warunków itp.

Można również uwzględnić inne, bardziej zaawansowane operatory, gdzie włączenie lub wykluczenie niektórych operatorów prowadzi do powstania rodziny algebr.

Wstęp

Algebrze relacyjnej poświęcono niewiele uwagi poza czystą matematyką aż do opublikowania relacyjnego modelu danych EF Codda w 1970 r. Codd zaproponował taką algebrę jako podstawę dla języków zapytań do baz danych. (Zobacz sekcję Implementacje .)

Pięć prymitywnych operatorów algebry Codda to wybór , rzut , iloczyn kartezjański (zwany także iloczynem krzyżowym lub łączeniem krzyżowym ), suma zbiorów i różnica zbiorów .

Ustaw operatorów

Algebra relacyjna używa sumy zbiorów , różnicy zbiorów i iloczynu kartezjańskiego z teorii mnogości , ale dodaje dodatkowe ograniczenia do tych operatorów.

W przypadku unii zestawów i różnicy zestawów obie zaangażowane relacje muszą być zgodne ze związkami — to znaczy, że dwie relacje muszą mieć ten sam zestaw atrybutów. Ponieważ przecięcie zbioru jest zdefiniowane w kategoriach sumy zbiorów i różnicy zbiorów, dwie relacje zaangażowane w przecięcie zbioru również muszą być zgodne z sumą.

Aby można było zdefiniować iloczyn kartezjański, dwie zaangażowane relacje muszą mieć rozłączne nagłówki — to znaczy nie mogą mieć wspólnej nazwy atrybutu.

Ponadto iloczyn kartezjański jest definiowany inaczej niż w teorii mnogości w tym sensie, że krotki są uważane za „płytkie” dla celów operacji. Oznacza to, że iloczyn kartezjański zbioru n -krotek ze zbiorem m -krotek daje zbiór „spłaszczonych” ( n + m ) -krotek (podczas gdy podstawowa teoria mnogości zalecałaby zbiór 2-krotek, z których każda zawierający n -krotkę i m -krotkę). Bardziej formalnie R × S jest zdefiniowany w następujący sposób:

$${\ Displaystyle R \ razy S: = \ {(r_ {1}, r_ {2}, \ kropki, r_ {n}, s_ {1}, s_ {2}, \ kropki, s_ {m})|(r_{1},r_{2},\kropki ,r_{n})\w R,(s_{1},s_{2},\kropki ,s_{m})\w S \}}$$

Liczność iloczynu kartezjańskiego jest iloczynem liczności jego czynników, czyli | R × S | = | R | × | S |.

projekcja ( Π )

Główny artykuł: Projekcja (algebra relacyjna)

Projekcja jest $_$ operacją jako a _ ${\ displaystyle a_ {1}, \ ldots, a_ {n}}$ to zestaw nazw atrybutów. Wynik takiej projekcji definiuje się jako zbiór , który otrzymuje się, gdy wszystkie krotki w R są ograniczone do zbioru ${\ Displaystyle \ {a_ {1}, \ ldots, a_ {n} \}}$ .

Uwaga: po zaimplementowaniu w standardzie SQL „projekcja domyślna” zwraca multiset zamiast zestawu, a projekcja Π w celu wyeliminowania zduplikowanych danych jest uzyskiwana przez dodanie słowa kluczowego DISTINCT .

Wybór ( σ )

Główny artykuł: Wybór (algebra relacyjna)

Uogólniony wybór to jednoargumentowa operacja zapisana jako ${\ Displaystyle \ sigma _ {\ varphi} (R)}$ gdzie φ jest formułą zdaniową , która składa się z atomów dozwolonych w selekcji normalnej i operatorów logicznych ${ \ Displaystyle \ klin}$ ( i ), ${\ Displaystyle \ lor}$ ( lub ) i ${\ Displaystyle \ neg}$ ( negacja ). Ten wybór wybiera wszystkie te krotki w R , dla których zachodzi φ .

$lub współpracowników$ , wybór można zapisać . Wynikiem byłaby relacja zawierająca każdy atrybut każdego unikalnego rekordu, gdzie isFriend jest prawdą lub gdzie isBusinessContact jest prawdą.

Zmień nazwę ( ρ )

Główny artykuł: Zmień nazwę (algebra relacyjna)

Zmiana nazwy to operacja jednoargumentowa $że$ jako , gdzie wynik jest identyczny z R , z wyjątkiem atrybutu wszystkich krotkach została zmieniona a atrybut. Jest to po prostu używane do zmiany nazwy atrybutu relacji lub samej relacji.

$isBusinessContact$ ” w relacji , .

Istnieje również notacja ${\ Displaystyle \ rho _ {x (A_ {1}, \ ldots, A_ {n})} (R$ ) } nazwę na x a nazwy atrybutów na $}}$${\ Displaystyle \ {A_ {1}, \ ldots, A_ {n} \}}$ .

Łączenia i operatory podobne do łączników

Połączenie naturalne (⋈)

„Naturalne łączenie” przekierowuje tutaj. Aby zapoznać się z implementacją języka SQL, zobacz Łączenie naturalne (SQL) .

„⋈” przekierowuje tutaj. Aby zapoznać się z zespołem czasami reprezentowanym przez ten symbol, zobacz The Armed .

Złączenie naturalne (⋈) to operator binarny zapisany jako ( R ⋈ S ), gdzie R i S to relacje . Wynikiem łączenia naturalnego jest zbiór wszystkich kombinacji krotek w R i S , które są równe pod względem wspólnych nazw atrybutów. Jako przykład rozważmy tabele Pracownik i Dział oraz ich naturalne połączenie:

Pracownik

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Wypad	2241	Obroty
Jerzy	3401	Finanse
Harriet	2202	Obroty
Maryja	1257	Zasoby ludzkie

Dział

NazwaDepartamentu	Menedżer
Finanse	Jerzy
Obroty	Harriet
Produkcja	Karol

Pracownik ⋈ Dział

Nazwa	Identyfikator Empl	NazwaDepartamentu	Menedżer
Złupić	3415	Finanse	Jerzy
Wypad	2241	Obroty	Harriet
Jerzy	3401	Finanse	Jerzy
Harriet	2202	Obroty	Harriet

Zwróć uwagę, że w wyniku nie pojawia się ani pracownik o imieniu Mary, ani dział produkcji.

Można to również wykorzystać do zdefiniowania składu relacji . Na przykład skład Pracownika i Działu to ich połączenie, jak pokazano powyżej, rzutowane na wszystkie oprócz wspólnego atrybutu NazwaDepartamentu . W teorii kategorii połączeniem jest właśnie produkt włóknisty .

Złączenie naturalne jest prawdopodobnie jednym z najważniejszych operatorów, ponieważ jest relacyjnym odpowiednikiem operatora logicznego AND. Zauważ, że jeśli ta sama zmienna występuje w każdym z dwóch predykatów połączonych operatorem AND, to ta zmienna oznacza to samo i oba wystąpienia muszą być zawsze zastąpione tą samą wartością (jest to konsekwencja idempotencji logicznego AND ) . W szczególności łączenie naturalne umożliwia łączenie relacji powiązanych kluczem obcym . Na przykład w powyższym przykładzie klucz obcy prawdopodobnie przechowuje od Employee . Nazwa działu do Dział _ NazwaDepartamentu , a następnie naturalne połączenie Pracownika i Działu łączy wszystkich pracowników z ich działami. Działa to, ponieważ klucz obcy jest przechowywany między atrybutami o tej samej nazwie. Jeśli tak nie jest, na przykład w kluczu obcym z Dept. Menedżer do pracownika . Nazwij, a następnie należy zmienić nazwy tych kolumn przed wykonaniem łączenia naturalnego. Takie połączenie jest czasem nazywane równorzędnym ( patrz θ -join).

Bardziej formalnie semantyka łączenia naturalnego jest zdefiniowana w następujący sposób:

${\ Displaystyle R \ muszka S = \ lewo \ {r \ kubek s \ \ vert \ r \ w R \ \ ziemia \ s \ w S \ \ ziemia \ {\ mathit {zabawa}} (r \ kubek s) \ prawo \}}$

 

 

 

 

()

gdzie Fun(t) jest predykatem , który jest prawdziwy dla relacji t (w sensie matematycznym), jeśli t jest funkcją (tj. t nie odwzorowuje żadnego atrybutu na wiele wartości). Zwykle wymagane jest, aby R i S miały co najmniej jeden wspólny atrybut, ale jeśli to ograniczenie zostanie pominięte, a R i S nie mają wspólnych atrybutów, wówczas połączenie naturalne staje się dokładnie iloczynem kartezjańskim.

Naturalne łączenie można symulować za pomocą prymitywów Codda w następujący sposób. Załóżmy, że c ₁ ,..., cm to nazwy atrybutów wspólne dla R i S , r ₁ ,..., r _n to nazwy atrybutów unikalne dla R i s ₁ ,..., s _{k to} atrybuty nazwy unikalne dla S. Ponadto załóżmy, że nazwy atrybutów x ₁ ,..., x _m nie są ani w R , ani w S. W pierwszym kroku wspólne nazwy atrybutów w S mogą zostać zmienione:

${\ Displaystyle T = \ rho _ {x_ {1} / c_ {1}, \ ldots, x_ {m} / c_ {m}} (S) = \ rho _ {x_ {1} / c_ {1}} (\rho _{x_{2}/c_{2}}(\ldots \rho _{x_{m}/c_{m}}(S)\ldots ))}$

 

 

 

 

()

Następnie bierzemy iloczyn kartezjański i wybieramy krotki, które mają zostać połączone:

${\ Displaystyle P = \ sigma _ {c_ {1} = x_ {1}, \ ldots, c_ {m} = x_ {m}} (R \ razy T) = \ sigma _ {c_ {1} = x_ { 1}}(\sigma _{c_{2}=x_{2}}(\ldots \sigma _{c_{m}=x_{m}}(R\razy T)\ldots ))}$

 

 

 

 

()

Na koniec wykonujemy projekcję, aby pozbyć się atrybutów o zmienionych nazwach:

${\ Displaystyle U = \ Pi _ {r_ {1}, \ ldots, r_ {n} ,c_{1},\ldots,c_{m},s_{1},\ldots,s_{k}}(P)}$

 

 

 

 

()

θ -łączenie i równorzędne łączenie

Rozważ tabele Samochód i Łódź , które zawierają modele samochodów i łodzi oraz ich ceny. Załóżmy, że klient chce kupić samochód i łódź, ale nie chce wydawać więcej pieniędzy na łódź niż na samochód. Połączenie θ (⋈ _θ ) na predykacie CarPrice ≥ BoatPrice tworzy spłaszczone pary wierszy, które spełniają predykat. W przypadku użycia warunku, w którym atrybuty są równe, na przykład Cena, warunek można określić jako Cena = Cena lub alternatywnie ( Cena ) sama.

Samochód

Model samochodu	Cena samochodu
Samochód A	20 000
Węglowodany	30 000
Samochód C	50 000

Łódź

Model łodzi	Cena łodzi
Łódź1	10 000
Łódź2	40 000
Łódź3	60 000

$\ muszka Boat \ na szczycie \ scriptstyle CarPrice \ geq BoatPrice}$

Model samochodu	Cena samochodu	Model łodzi	Cena łodzi
Samochód A	20 000	Łódź1	10 000
Węglowodany	30 000	Łódź1	10 000
Samochód C	50 000	Łódź1	10 000
Samochód C	50 000	Łódź2	40 000

Aby połączyć krotki z dwóch relacji, gdzie warunkiem połączenia nie jest po prostu równość wspólnych atrybutów, wygodnie jest mieć bardziej ogólną postać operatora łączenia, którym jest θ -join ( lub theta-join). θ -join to operator binarny zapisany jako $theta \ b}}$ \ lub $v}}$${\ Displaystyle {R \ \$ bowtie \ S \atop a\ \theta \ gdzie aib to nazwy atrybutów, θ to binarny operator relacyjny w zbiorze {<, ≤, =, ≠, >, ≥} , υ to stała wartości, a R i S to relacje. Wynik tej operacji składa się ze wszystkich kombinacji krotek w R i S , które spełniają θ . Wynik połączenia θ jest zdefiniowany tylko wtedy, gdy nagłówki S i R są rozłączne, to znaczy nie zawierają wspólnego atrybutu.

Symulacja tej operacji w operacjach podstawowych jest zatem następująca:

R ⋈ _θ S = σ _θ ( R × S )

W przypadku, gdy operator θ jest operatorem równości (=), to łączenie jest również nazywane łączeniem równym .

Należy jednak zauważyć, że język komputerowy, który obsługuje operatory łączenia naturalnego i selekcji, nie potrzebuje również θ -join, ponieważ można to osiągnąć poprzez wybór z wyniku łączenia naturalnego (które degeneruje się do iloczynu kartezjańskiego, gdy nie ma wspólnych atrybuty).

W implementacjach języka SQL łączenie na podstawie predykatu jest zwykle nazywane łączeniem wewnętrznym , a słowo kluczowe on umożliwia określenie predykatu używanego do filtrowania wierszy. Należy zauważyć, że utworzenie spłaszczonego iloczynu kartezjańskiego, a następnie filtrowanie wierszy jest koncepcyjnie poprawne, ale implementacja używałaby bardziej wyrafinowanych struktur danych, aby przyspieszyć zapytanie łączące.

Semijoin (⋉ i ⋊)

Lewe $semijoin$$to$ połączenie podobne do naturalnego zapisane gdzie i $.$ Rezultatem jest zbiór wszystkich krotek w, $równa$ których istnieje krotka w, $jest$ ich wspólnym nazwom atrybutów. Różnica w stosunku do łączenia naturalnego polega na tym, że inne kolumny ${\ displaystyle S}$ nie pojawiają się. Rozważmy na przykład tabele Pracownik i Dział oraz ich semijoin:

Pracownik

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Wypad	2241	Obroty
Jerzy	3401	Finanse
Harriet	2202	Produkcja

Dział

NazwaDepartamentu	Menedżer
Obroty	Wypad
Produkcja	Harriet

Pracownik ⋉ Dział

Nazwa	Identyfikator Empl	NazwaDepartamentu
Wypad	2241	Obroty
Harriet	2202	Produkcja

Bardziej formalnie semantykę semijoin można zdefiniować w następujący sposób:

${\ Displaystyle R \ ltimes S = \ {t: t \ w R \ ziemia \ istnieje s \ w S ( \operatorname {zabawa} (t\cup s))\}}$

gdzie ${\ Displaystyle \ operatorname {Zabawa} (r)}$ jest taka, jak w definicji łączenia naturalnego.

Semijoin można symulować za pomocą naturalnego łączenia w następujący sposób. Jeśli $\ displaystyle a_ {1}, \ ldots, a_ {n}}$ są nazwami atrybutów ${\ displaystyle R}$ , to

${\ Displaystyle R \ ltimes S = \ Pi _ {a_ {1}, \ ldots, a_ {n}} (R \ muszka S).}$

Ponieważ możemy symulować naturalne łączenie za pomocą podstawowych operatorów, wynika z tego, że dotyczy to również semijoin.

W artykule Codda z 1970 roku semijoin nazywa się ograniczeniem.

Antijoin (▷)

Sprzężenie przeciwstawne, zapisane jako R ▷ S , gdzie R i S są relacjami , jest podobne do sprzężenia półprzewodnikowego, ale wynikiem połączenia przeciwstawnego są tylko te krotki w R , dla których nie ma krotki w S równej ich wspólnym nazwom atrybutów.

Jako przykład rozważmy tabele Pracownik i Dział oraz ich antijoin:

Pracownik

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Wypad	2241	Obroty
Jerzy	3401	Finanse
Harriet	2202	Produkcja

Dział

NazwaDepartamentu	Menedżer
Obroty	Wypad
Produkcja	Harriet

Pracownik ▷ Dział

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Jerzy	3401	Finanse

Antijoin jest formalnie zdefiniowany w następujący sposób:

R ▷ S = { t : t ∈ R ∧ ¬∃ s ∈ S ( Zabawa ( t ∪ s )) }

Lub

R ▷ S = { t : t ∈ R , nie ma krotki s z S , która spełnia Fun ( t ∪ s ) }

gdzie Fun ( t ∪ s ) jest jak w definicji łączenia naturalnego.

Antijoin można również zdefiniować jako uzupełnienie semijoin w następujący sposób:

R ▷ S = R - R ⋉ S

 

 

 

 

()

Biorąc to pod uwagę, antijoin jest czasami nazywany anti-semijoin, a operator antijoin jest czasami zapisywany jako symbol semijoin z kreską nad nim, zamiast ▷.

Podział (÷)

Dzielenie jest operacją binarną zapisaną jako R ÷ S . Dzielenie nie jest realizowane bezpośrednio w SQL. Wynik składa się z ograniczeń krotek w R do nazw atrybutów unikalnych dla R , tj. w nagłówku R , ale nie w nagłówku S , co oznacza, że ​​wszystkie ich kombinacje z krotkami w S są obecne w R . Dla przykładu zobacz tabele Completed , DBProject i ich podział:

Zakończony

Student	Zadanie	Identyfikator pokoju
Fred	Baza danych1	174
Fred	Baza danych2	123
Fred	Kompilator1	234
Eugeniusz	Baza danych1	671
Eugeniusz	Kompilator1	829
Sara	Baza danych1	246
Sara	Baza danych2	934

DBProjekt

Zadanie	Identyfikator zadania
Baza danych1	42
Baza danych2	91

Ukończono ÷ DBProject

Student
Fred
Sarah

Jeśli DBProject zawiera wszystkie zadania projektu Baza danych, to wynik powyższego podziału zawiera dokładnie uczniów, którzy wykonali oba zadania w projekcie Baza danych. Bardziej formalnie semantyka podziału jest zdefiniowana w następujący sposób:

R ÷ S = { t [ za ₁ ,..., za _n ] : t ∈ R ∧ ∀ s ∈ S ( ( t [ za ₁ ,..., za _n ] ∪ s ) ∈ R ) }

 

 

 

 

()

gdzie { a ₁ ,..., a _n } jest zbiorem nazw atrybutów unikalnych dla R , a t [ a ₁ ,..., a _n ] jest ograniczeniem t do tego zbioru. Zwykle wymagane jest, aby nazwy atrybutów w nagłówku S były podzbiorem nazw atrybutów R , ponieważ w przeciwnym razie wynik operacji będzie zawsze pusty.

Symulacja dzielenia z podstawowymi operacjami jest następująca. Zakładamy, że a ₁ ,..., a _n to nazwy atrybutów unikalne dla R , a b ₁ ,..., b _m to nazwy atrybutów S . W pierwszym kroku projektujemy R na jego unikalne nazwy atrybutów i konstruujemy wszystkie kombinacje z krotkami w S :

T := π _{za 1 ,..., za n} ( R ) × S

W poprzednim przykładzie T oznaczałoby taką tabelę, w której każdy Uczeń (ponieważ Uczeń jest unikalnym kluczem/atrybutem tabeli Ukończone) jest łączony z każdym danym Zadaniem. Na przykład Eugene miałby dwa wiersze, Eugene → Database1 i Eugene → Database2 w T.

EG: Najpierw udawajmy, że „Completed” ma trzeci atrybut o nazwie „stopień”. To niechciany bagaż tutaj, więc musimy go zawsze projektować. W rzeczywistości w tym kroku możemy również usunąć „Zadanie” z R; mnożenie stawia go z powrotem.

T := π _Student ( R ) × S // To daje nam każdą możliwą pożądaną kombinację, w tym te, które w rzeczywistości nie istnieją w R i wyklucza inne (np. Fred | kompilator1, który nie jest kombinacją pożądaną)

T

Student	Zadanie
Fred	Baza danych1
Fred	Baza danych2
Eugeniusz	Baza danych1
Eugeniusz	Baza danych2
Sara	Baza danych1
Sara	Baza danych2

W kolejnym kroku odejmujemy R od T

związek :

U := T − R

W U mamy możliwe kombinacje, które „mogły” być w R , ale nie były.

EG: Ponownie z projekcjami — T i R muszą mieć identyczne nazwy/nagłówki atrybutów.

U := T − π _Student,Task ( R ) // To daje nam listę „czego brakuje”.

T

Student	Zadanie
Fred	Baza danych1
Fred	Baza danych2
Eugeniusz	Baza danych1
Eugeniusz	Baza danych2
Sara	Baza danych1
Sara	Baza danych2

Raka Ukończono _

Student	Zadanie
Fred	Baza danych1
Fred	Baza danych2
Fred	Kompilator1
Eugeniusz	Baza danych1
Eugeniusz	Kompilator1
Sara	Baza danych1
Sara	Baza danych2

U

aka

T − R

czyli

czego brakuje

Student	Zadanie
Eugeniusz	Baza danych2

Więc jeśli weźmiemy teraz projekcję na nazwy atrybutów unikalne dla R

wtedy mamy ograniczenia krotek w R , dla których nie wszystkie kombinacje z krotkami w S były obecne w R :

V := π _{a 1 ,..., a n} ( U )

EG: Rzut U w dół tylko do danych atrybutów (Student)

V := π _Student ( U )

V

uczeń
Eugeniusz

Więc co pozostaje do zrobienia, to wziąć projekcję R na jej unikalne nazwy atrybutów i odjąć te w V :

W := π _{za 1 ,..., za n} ( R ) - V

EG: W := π _Student ( R ) - V .

π _Student ( R )

Student
Fred
Eugene
Sarah

V

uczeń
Eugeniusz

Waka

(π _Student ( R − V )

czyli

pożądany wynik

Student

)
Fred
Sarah

Wspólne rozszerzenia

W praktyce opisana powyżej klasyczna algebra relacyjna jest rozszerzana o różne operacje, takie jak łączenia zewnętrzne, funkcje agregujące, a nawet domknięcie przechodnie.

Łączenia zewnętrzne

Zobacz też: Łączenie (SQL) § Łączenie zewnętrzne

Podczas gdy wynik złączenia (lub złączenia wewnętrznego) składa się z krotek utworzonych przez połączenie pasujących krotek w dwóch operandach, złączenie zewnętrzne zawiera te krotki i dodatkowo kilka krotek utworzonych przez rozszerzenie niedopasowanej krotki w jednym z operandów o wartości „wypełnij” dla każdego z atrybutów drugiego operandu. Złączenia zewnętrzne nie są uważane za część omówionej dotychczas klasycznej algebry relacyjnej.

Operatory zdefiniowane w tej sekcji zakładają istnienie wartości pustej ω , której nie definiujemy, która ma być używana jako wartości wypełnienia; w praktyce odpowiada to NULL w SQL. Aby kolejne operacje selekcji na wynikowej tabeli miały sens, wartościom zerowym należy przypisać znaczenie semantyczne; w podejściu Codda logika zdaniowa używana przez wybór jest rozszerzona na logikę trójwartościową , chociaż pomijamy te szczegóły w tym artykule.

Zdefiniowane są trzy operatory łączenia zewnętrznego: lewe łączenie zewnętrzne, prawe łączenie zewnętrzne i pełne łączenie zewnętrzne. (Słowo „zewnętrzny” jest czasami pomijane).

Lewe sprzężenie zewnętrzne (⟕)

Lewe sprzężenie zewnętrzne jest zapisywane jako R⟕S , gdzie R i S to relacje . Wynikiem lewego sprzężenia zewnętrznego jest zestaw wszystkich kombinacji krotek w R i S , które są równe pod względem ich wspólnych nazw atrybutów, oprócz (luźno mówiąc) krotek w R , które nie mają pasujących krotek w S .

Jako przykład rozważmy tabele Pracownik i Dział oraz ich lewe sprzężenie zewnętrzne:

Pracownik

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Wypad	2241	Obroty
Jerzy	3401	Finanse
Harriet	2202	Obroty
Tim	1123	Wykonawczy

Dział

NazwaDepartamentu	Menedżer
Obroty	Harriet
Produkcja	Karol

Pracownik ⟕ Dział

Nazwa	Identyfikator Empl	NazwaDepartamentu	Menedżer
Złupić	3415	Finanse	ω
Wypad	2241	Obroty	Harriet
Jerzy	3401	Finanse	ω
Harriet	2202	Obroty	Harriet
Tim	1123	Wykonawczy	ω

W wynikowej relacji krotki w S , które nie mają wspólnych wartości we wspólnych nazwach atrybutów z krotkami w R , przyjmują wartość pustą , ω .

Dept nie ma krotek o nazwie DeptName Finance lub Executive , w wynikowej relacji występują ω , w których krotki w Employee mają DeptName of Finance lub Executive .

Niech r ₁ , r ₂ , ..., r _n będą atrybutami relacji R i niech {( ω , ..., ω )} będą pojedynczą relacją na atrybutach, które są unikalne dla relacji S (te, które nie są atrybutami R ). Wtedy lewe sprzężenie zewnętrzne można opisać w kategoriach łączenia naturalnego (a zatem przy użyciu podstawowych operatorów) w następujący sposób:

${\ Displaystyle (R \ muszka S) \ puchar ( (R-\pi _{r_{1},r_{2},\kropki,r_{n}}(R\muszka S))\razy \{(\omega,\kropki,\omega)\})}$

Prawe sprzężenie zewnętrzne (⟖)

Prawe sprzężenie zewnętrzne zachowuje się prawie identycznie jak lewe sprzężenie zewnętrzne, ale role tabel są zamienione.

Prawe sprzężenie zewnętrzne relacji R i S jest zapisywane jako R ⟖ S . Wynikiem prawego sprzężenia zewnętrznego jest zestaw wszystkich kombinacji krotek w R i S , które są równe pod względem ich wspólnych nazw atrybutów, oprócz krotek w S , które nie mają pasujących krotek w R .

Rozważmy na przykład tabele Pracownik i Dział oraz ich prawe sprzężenie zewnętrzne:

Pracownik

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Wypad	2241	Obroty
Jerzy	3401	Finanse
Harriet	2202	Obroty
Tim	1123	Wykonawczy

Dział

NazwaDepartamentu	Menedżer
Obroty	Harriet
Produkcja	Karol

Pracownik ⟖ Dział

Nazwa	Identyfikator Empl	NazwaDepartamentu	Menedżer
Wypad	2241	Obroty	Harriet
Harriet	2202	Obroty	Harriet
ω	ω	Produkcja	Karol

W wynikowej relacji krotki w R , które nie mają wspólnych wartości we wspólnych nazwach atrybutów z krotkami w S , przyjmują wartość pustą , ω .

Ponieważ nie ma krotek w pracowniku z nazwą działu produkcji , w atrybutach Name i EmpId wynikowej relacji występują ω , w których krotki w dziale miały nazwę działu produkcji .

Niech s ₁ , s ₂ , ..., s _n będą atrybutami relacji S i niech {( ω , ..., ω )} będą pojedynczą relacją na atrybutach, które są unikalne dla relacji R (tych, które nie są atrybutami S ). Następnie, podobnie jak w przypadku lewego łączenia zewnętrznego, prawe łączenie zewnętrzne można symulować za pomocą naturalnego łączenia w następujący sposób:

${\ Displaystyle (R \ muszka S) \ puchar ( \{(\omega,\kropki,\omega)\}\razy (S-\pi _{s_{1},s_{2},\dots,s_{n}}(R\muszka S)))}$

Pełne sprzężenie zewnętrzne (⟗)

Łączenie zewnętrzne lub pełne łączenie zewnętrzne w efekcie łączy wyniki lewego i prawego łączenia zewnętrznego.

Pełne sprzężenie zewnętrzne jest zapisywane jako R⟗S , gdzie R i S to relacje . Wynikiem pełnego sprzężenia zewnętrznego jest zestaw wszystkich kombinacji krotek w R i S , które są równe pod względem ich wspólnych nazw atrybutów, oprócz krotek w S , które nie mają pasujących krotek w R i krotek w R , które nie mają pasujących krotek w S w ich wspólnych nazwach atrybutów.

Jako przykład rozważmy tabele Pracownik i Dział oraz ich pełne sprzężenie zewnętrzne:

Pracownik

Nazwa	Identyfikator Empl	NazwaDepartamentu
Złupić	3415	Finanse
Wypad	2241	Obroty
Jerzy	3401	Finanse
Harriet	2202	Obroty
Tim	1123	Wykonawczy

Dział

NazwaDepartamentu	Menedżer
Obroty	Harriet
Produkcja	Karol

Pracownik ⟗ Dział

Nazwa	Identyfikator Empl	NazwaDepartamentu	Menedżer
Złupić	3415	Finanse	ω
Wypad	2241	Obroty	Harriet
Jerzy	3401	Finanse	ω
Harriet	2202	Obroty	Harriet
Tim	1123	Wykonawczy	ω
ω	ω	Produkcja	Karol

W wynikowej relacji krotki w R , które nie mają wspólnych wartości we wspólnych nazwach atrybutów z krotkami w S , przyjmują wartość pustą , ω . Krotki w S , które nie mają wspólnych wartości we wspólnych nazwach atrybutów z krotkami w R , również przyjmują wartość pustą , ω .

Pełne łączenie zewnętrzne można symulować za pomocą lewego i prawego łączenia zewnętrznego (a tym samym naturalnego łączenia i łączenia zestawów) w następujący sposób:

R ⟗ S = ( R ⟕ S ) ∪ ( R ⟖ S )

Operacje dla obliczeń dziedzinowych

Do tej pory w algebrze relacyjnej nie wprowadzono niczego, co pozwoliłoby na obliczenia w domenach danych (poza oceną wyrażeń zdaniowych obejmujących równość). Nie da się np. za pomocą samej algebry wprowadzonej do tej pory napisać wyrażenia, które mnoży liczby z dwóch kolumn, np. cenę jednostkową przez ilość, aby otrzymać cenę całkowitą. Praktyczne języki zapytań mają takie ułatwienia, np. SQL SELECT pozwala operacjom arytmetycznym definiować nowe kolumny w wyniku SELECT cena_jednostkowa * ilość AS cena_całkowita FROM t , a podobne ułatwienie jest wyraźniej zapewniane przez słowo kluczowe EXTEND Samouczka D. W teorii baz danych nazywa się to projekcją rozszerzoną .

Zbiór

Co więcej, obliczanie różnych funkcji na kolumnie, takich jak sumowanie jej elementów, również nie jest możliwe przy użyciu wprowadzonej do tej pory algebry relacyjnej. Istnieje pięć funkcji agregujących , które są dołączone do większości systemów relacyjnych baz danych. Operacje te to suma, liczba, średnia, maksimum i minimum. _W algebrze relacji operacja agregacji na schemacie ( A ₁ , A ₂ , ... An ) jest zapisana w następujący sposób:

${\ Displaystyle G_ {1}, G_ {2 },\ldots,G_{m}\ g_{f_{1}({A_{1}}'),f_{2}({A_{2}}'),\ldots,f_{k}({A_ {k}}')}\ (r)}$

gdzie każdy A _j ', 1 ≤ j ≤ k , jest jednym z pierwotnych atrybutów A _i , 1 ≤ i ≤ n .

Atrybuty poprzedzające g to atrybuty grupujące, które działają jak klauzula „grupuj według” w SQL. Następnie istnieje dowolna liczba funkcji agregujących zastosowanych do poszczególnych atrybutów. Operacja jest stosowana do dowolnej relacji r . Atrybuty grupowania są opcjonalne, a jeśli nie są podane, funkcje agregacji są stosowane w całej relacji, do której stosowana jest operacja.

Załóżmy, że mamy tabelę o nazwie Konto z trzema kolumnami, a mianowicie Numer_konta, Nazwa_oddziału i Saldo . Chcemy znaleźć maksymalne saldo każdej gałęzi. Jest to realizowane przez _{Branch_Name} G _{Max( Balance )} ( Account ). Aby znaleźć najwyższe saldo wszystkich rachunków, niezależnie od oddziału, możemy po prostu napisać G _{Max( Saldo )} ( Konto ).

Grupowanie jest często zapisywane jako _{Branch_Name} ɣ _{Max( Balance )} ( Account ).

Zamknięcie przejściowe

Chociaż algebra relacyjna wydaje się wystarczająco potężna do większości praktycznych celów, istnieje kilka prostych i naturalnych operatorów relacji , których nie można wyrazić za pomocą algebry relacyjnej. Jednym z nich jest domknięcie przechodnie relacji binarnej. Mając dziedzinę D , niech relacja binarna R będzie podzbiorem D × D . Domknięcie przechodnie R ⁺ R jest najmniejszym podzbiorem D × D , który zawiera R i spełnia następujący warunek:

${\ Displaystyle \ forall x \ forall y \ forall z \ lewo ((( x,y)\in R^{+}\klin (y,z)\in R^{+}\Strzałka w prawo (x,z)\in R^{+}\right)}$

Można to udowodnić na podstawie faktu, że nie istnieje wyrażenie algebry relacyjnej E ( R ) przyjmujące R jako argument zmienny, który daje R ⁺ .

Jednak SQL oficjalnie obsługuje takie zapytania o punkty stałe od 1999 roku i miał rozszerzenia specyficzne dla dostawcy w tym kierunku na długo przedtem.

Wykorzystanie właściwości algebraicznych do optymalizacji zapytań

Dwa możliwe plany zapytań dla zapytania trójkątnego R(A, B) ⋈ S(B, C) ⋈ T(A, C) ; pierwsze jioins S i T i łączy wynik z R , drugie łączy najpierw R i S i łączy wynik z T

Systemy zarządzania relacyjnymi bazami danych często zawierają optymalizator zapytań , który próbuje określić najbardziej efektywny sposób wykonania danego zapytania. Optymalizatory zapytań wyliczają możliwe plany zapytań , szacują ich koszt i wybierają plan o najniższym szacowanym koszcie. Jeśli zapytania są reprezentowane przez operatory z algebry relacyjnej, optymalizator zapytań może wyliczyć możliwe plany zapytań, przepisując początkowe zapytanie przy użyciu właściwości algebraicznych tych operatorów.

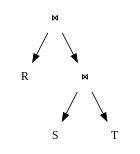
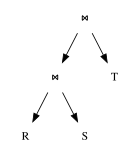
Zapytania mogą być reprezentowane jako drzewo , gdzie

• węzły wewnętrzne są operatorami,
• liście to relacje ,
• poddrzewa są podwyrażeniami.

Podstawowym celem optymalizatora zapytań jest przekształcenie drzew wyrażeń w równoważne drzewa wyrażeń, w których średni rozmiar relacji uzyskanych przez podwyrażenia w drzewie jest mniejszy niż przed optymalizacją . Celem drugorzędnym jest próba utworzenia wspólnych wyrażeń podrzędnych w ramach pojedynczego zapytania lub, jeśli w tym samym czasie ocenianych jest więcej niż jedno zapytanie, we wszystkich tych zapytaniach. Uzasadnieniem drugiego celu jest to, że wystarczy raz obliczyć wspólne podwyrażenia, a wyniki mogą być używane we wszystkich zapytaniach zawierających to podwyrażenie.

Oto zestaw reguł, które można zastosować w takich przekształceniach.

Wybór

Reguły dotyczące operatorów wyboru odgrywają najważniejszą rolę w optymalizacji zapytań. Selection jest operatorem, który bardzo skutecznie zmniejsza liczbę wierszy w swoim argumencie, więc jeśli selekcje w drzewie wyrażeń zostaną przesunięte w kierunku liści, wewnętrzne relacje (wytworzone przez podwyrażenia) prawdopodobnie się zmniejszą.

Podstawowe właściwości selekcji

Wybór jest idempotentny (wiele zastosowań tego samego wyboru nie ma dodatkowego efektu poza pierwszym) i przemienny (kolejność wyboru nie ma wpływu na ostateczny wynik).

1. ${\ Displaystyle \ sigma _ {A} (R) = \ sigma _ {A} \ sigma _ {A} (R) \, \!}$
2. ${\ Displaystyle \ sigma _ {A} \ sigma _ {B} (R) = \ sigma _ {B} \ sigma _ {A} (R) \ ,\!}$

Rozbijanie selekcji ze złożonymi warunkami

Wybór, którego warunkiem jest koniunkcja prostszych warunków, jest równoważny z sekwencją wyborów z tymi samymi indywidualnymi warunkami, a wybór, którego warunkiem jest dysjunkcja, jest równoważny zsumowaniu wyborów. Tożsamości te mogą być używane do łączenia selekcji, tak aby mniej selekcji wymagało oceny, lub do ich dzielenia, tak aby selekcje komponentów mogły być przenoszone lub optymalizowane oddzielnie.

1. ${\ Displaystyle \ sigma _ {A \ ziemia B} (R) = \ sigma _ {A} ( \sigma _{B}(R))=\sigma _{B}(\sigma _{A}(R))}$
2. ${\ Displaystyle \ sigma _ {A \ lor B} (R) = \ sigma _ {A} (R) \ kubek \ sigma _ { B}(R)}$

Selekcja i produkt krzyżowy

Produkt krzyżowy jest najbardziej kosztownym operatorem do oceny. Jeśli relacje wejściowe mają N i M $wiersze$ wynik będzie zawierał . Dlatego ważne jest, aby zmniejszyć rozmiar obu operandów przed zastosowaniem operatora iloczynu krzyżowego.

Można to skutecznie zrobić, jeśli po iloczynie krzyżowym następuje operator wyboru, np. ${\ Displaystyle \ sigma _ {A} (R \ razy P)}$ . Biorąc pod uwagę definicję złączenia, jest to najbardziej prawdopodobny przypadek. Jeśli po iloczynie krzyżowym nie występuje operator wyboru, możemy spróbować przesunąć wybór z wyższych poziomów drzewa wyrażeń, korzystając z innych reguł wyboru.

$selekcji$ warunek A podzielony na warunki B , C i D przy reguł podziału dotyczących złożonych że B zawiera atrybuty tylko z R , C zawiera atrybuty tylko z P , a D zawiera część A zawierającą atrybuty z obu R i P. _ Zauważ, że B , C lub D są prawdopodobnie puste. Wtedy obowiązuje:

${\ Displaystyle \ sigma _ {A} (R \ razy P) =\sigma _{B\klin C\klin D}(R\razy P)=\sigma _{D}(\sigma _{B}(R)\czasy \sigma _{C}(P))}$

Operatory wyboru i zbioru

Selekcja jest rozdzielna względem ustalonych operatorów różnicy, przecięcia i sumy. Poniższe trzy reguły są używane do wypychania zaznaczenia poniżej operacji na zbiorach w drzewie wyrażeń. W przypadku operatorów różnicy zestawów i operatorów przecięcia możliwe jest zastosowanie operatora wyboru tylko do jednego z operandów następujących po transformacji. Może to być korzystne, gdy jeden z operandów jest mały, a narzut związany z oceną operatora wyboru przewyższa korzyści wynikające z zastosowania mniejszej relacji jako operandu.

1. ${\ Displaystyle \ sigma _ {A} (R \ setminus P) = \ sigma _ {A} ( R)\setminus \sigma _{A}(P)=\sigma _{A}(R)\setminus P}$
2. ${\ Displaystyle \ sigma _ {A} (R \ kubek P) = \ sigma _ {A} (R) \ kubek \ sigma _ { A}(P)}$
3. ${\ Displaystyle \ sigma _ {A} (R \ nasadka P) =\sigma _{A}(R)\cap \sigma _{A}(P)=\sigma _{A}(R)\cap P=R\cap \sigma _{A}(P)}$

Selekcja i projekcja

Selekcja zmienia się z projekcją wtedy i tylko wtedy, gdy pola, do których odwołuje się warunek selekcji, są podzbiorem zmiennych w projekcji. Wykonywanie selekcji przed projekcją może być przydatne, jeśli operand jest iloczynem krzyżowym lub połączeniem. W innych przypadkach, jeśli obliczenie warunku selekcji jest stosunkowo drogie, przeniesienie selekcji poza projekcję może zmniejszyć liczbę krotek, które należy przetestować (ponieważ projekcja może generować mniej krotek ze względu na eliminację duplikatów wynikających z pominiętych pól).

${\ Displaystyle \ pi _ {a_ {1}, \ ldots, a_ {n}} (\ sigma _ {A} (R)) = \ sigma _ {A} (\ pi _ {a_ {1}, \ ldots ,a_{n}}(R)){\text{ gdzie pola w }}A\subseteq \{a_{1},\ldots ,a_{n}\}}$

Występ

Podstawowe właściwości rzutowania

Projekcja jest idempotentna, więc seria (prawidłowych) projekcji jest równoważna najbardziej zewnętrznej projekcji.

${\ Displaystyle \ pi _ {a_ {1}, \ ldots, a_ {n}} (\ pi _ {b_ {1}, \ ldots, b_ {m}} (R)) = \ pi _ {a_ {1 },\ldots,a_{n}}(R){\text{gdzie }}\{a_{1},\ldots,a_{n}\}\subseteq \{b_{1},\ldots,b_{ M}\}}$

Operatory projekcji i zbiorów

Projekcja jest rozdzielcza w stosunku do ustalonej unii.

${\ Displaystyle \ pi _ {a_ {1}, \ ldots, a_ {n}} (R \ kubek P) = \ pi _ {a_ {1}, \ ldots, a_ {n}} (R) \ kubek \ pi _{a_{1},\ldots ,a_{n}}(P).\,}$

Projekcja nie rozkłada się na przecięciu i ustawionej różnicy. Kontrprzykłady podaje:

${\ Displaystyle \ pi _ {A} (\ {\ langle A = a, B = b\rangle \}\cap \{\langle A=a,B=b'\rangle \})=\pusty zbiór }$

${\ Displaystyle \ pi _ {A} (\ {\ langle A = a, B = b \ rangle \} )\cap \pi _{A}(\{\langle A=a,B=b'\rangle \})=\{\langle A=a\rangle \}}$

I

$\ Displaystyle \ pi _ {A} (\ {\ langle A=a,B=b\rangle \}\setminus \{\langle A=a,B=b'\rangle \})=\{\langle A=a\rangle \}}$

${\ Displaystyle \ pi _ {A} (\ {\ langle A = a, B = b \ rangle \})\setminus \pi _{A}(\{\langle A=a,B=b'\rangle \})=\pustyzbiór \,,}$

gdzie zakłada się, że b jest różne od b' .

Przemianować

Podstawowe właściwości zmiany nazwy

Kolejne zmiany nazw zmiennych można zwinąć w jedną zmianę nazwy. Operacje zmiany nazw, które nie mają wspólnych zmiennych, można dowolnie zmieniać względem siebie, co można wykorzystać do tego, aby kolejne zmiany nazw sąsiadowały ze sobą, aby można je było zwinąć.

1. $(R)) = \ rho _ { a/c}(R)\,\!}$
2. $\ Displaystyle \ rho _ {a/b} (\ rho _ {c/d} (R) )=\rho _{c/d}(\rho _{a/b}(R))\,\!}$

Zmień nazwę i ustaw operatorów

Zmiana nazwy jest rozdzielna względem ustalonej różnicy, sumy i przecięcia.

1. ${\ Displaystyle \ rho _ {a/b} (R \ setminus P) = \ rho _ {a/b }(R)\setminus \rho _{a/b}(P)}$
2. ${\ Displaystyle \ rho _ {a/b} (R \ kubek P) = \ rho _ {a/b }(R)\kielich \rho _{a/b}(P)}$
3. ${\ Displaystyle \ rho _ {a/b} (R \ czapka P) = \ rho _ {a/b }(R)\cap \rho _{a/b}(P)}$

Produkt i związek

Produkt kartezjański jest rozdzielny względem unii.

1. ${\ Displaystyle (A \ razy B) \ kubek (A \ razy C) = A \ razy (B \ kubek C)}$

Implementacje

Pierwszym językiem zapytań opartym na algebrze Codda była Alpha, opracowana przez samego dr Codda. Następnie ISBL , a ta pionierska praca została uznana przez wiele autorytetów za wskazującą drogę do przekształcenia pomysłu Codda w użyteczny język. Business System 12 był krótkotrwałym relacyjnym DBMS o sile branżowej, który wzorował się na ISBL.

W 1998 roku Chris Date i Hugh Darwen zaproponowali język o nazwie Tutorial D przeznaczony do nauczania teorii relacyjnych baz danych, a jego język zapytań również czerpie z pomysłów ISBL. Rel jest implementacją Tutorial D .

Nawet język zapytań SQL jest luźno oparty na algebrze relacyjnej, chociaż operandy w SQL ( tabele ) nie są dokładnie relacjami , a kilka użytecznych twierdzeń dotyczących algebry relacyjnej nie obowiązuje w odpowiedniku SQL (prawdopodobnie ze szkodą dla optymalizatorów i/ lub użytkowników). Model tabeli SQL to worek ( wielozbiór ), a nie zestaw. Na przykład wyrażenie jest twierdzeniem dla algebry relacyjnej na zbiorach, ale nie dla algebry relacyjnej $na$ omówienie algebry relacyjnej na torbach można znaleźć w rozdziale 5 podręcznika „Complete” autorstwa Garcii-Moliny , Ullmana i Widoma .

Zobacz też

• Produkt kartezjański
• D4 (język programowania) (implementacja D)
• Baza danych
• Logika krewnych
• Modelowanie roli obiektu
• Projekcja (matematyka)
• Projekcja (algebra relacyjna)
• Projekcja (teoria mnogości)
• Relacja
• Relacja (baza danych)
• Algebra relacji
• Skład relacji
• Budowa relacji
• Rachunek relacyjny
• Relacyjna baza danych
• Model relacyjny
• Teoria relacji
• Relacja triadyczna
• Krotkowy rachunek relacyjny
• SQL
• Dziennik danych
• Twierdzenie Codda

Dalsza lektura

Praktycznie każdy podręcznik akademicki dotyczący baz danych zawiera szczegółowe omówienie klasycznej algebry relacyjnej.

• Imieliński T. ; Lipski W. (1984). „Relacyjny model danych i algebry cylindryczne” . Journal of Computer and System Sciences . 28 : 80–102. doi : 10.1016/0022-0000(84)90077-1 . (Dla związku z algebrami cylindrycznymi ).

Linki zewnętrzne

• SZCZUR. Programowy tłumacz algebry relacyjnej na język SQL
• Filmy z wykładami: Przetwarzanie algebry relacyjnej — wprowadzenie do przetwarzania algebry relacyjnej w systemach baz danych
• Notatki do wykładu: Algebra relacyjna — Szybki samouczek dotyczący adaptacji zapytań SQL do algebry relacyjnej
• Relational – Graficzna implementacja algebry relacyjnej
• Query Optimization (Strona usunięta; Najbliższe alternatywy: Standford Query Optimization 2 , badania firmy Microsoft Query Optimization in relacial systems , artykuł Stanforda: Query Optimization ) Ten artykuł jest wprowadzeniem do wykorzystania algebry relacyjnej w optymalizacji zapytań i zawiera liczne cytaty dotyczące bardziej dogłębne badanie.
• Relacyjny system algebry dla Oracle i Microsoft SQL Server
• Pireal — eksperymentalne narzędzie edukacyjne do pracy z algebrą relacyjną
• DES – narzędzie edukacyjne do pracy z algebrą relacyjną i innymi językami formalnymi
• RelaX - Relational Algebra Calculator (oprogramowanie typu open source dostępne jako usługa online bez rejestracji)
• RA: tłumacz algebry relacyjnej
• Tłumaczenie języka SQL na algebrę relacyjną