Algorytm Marzullo

Algorytm Marzullo , wymyślony przez Keitha Marzullo na potrzeby jego doktoratu. rozprawa doktorska z 1984 r., to algorytm zgodności używany do wybierania źródeł do szacowania dokładnego czasu z wielu hałaśliwych źródeł czasu. Jego udoskonalona wersja, przemianowana na „ algorytm skrzyżowania ”, stanowi część nowoczesnego protokołu Network Time Protocol . Algorytm Marzullo jest również używany do obliczania swobodnego przecięcia n pudełek (lub bardziej ogólnie n podzbiorów R ⁿ ), zgodnie z wymaganiami kilku solidne metody estymacji zbiorów .

Zamiar

Algorytm Marzullo jest wydajny pod względem czasu do uzyskania optymalnej wartości ze zbioru oszacowań z przedziałami ufności , gdzie rzeczywista wartość może być poza przedziałem ufności dla niektórych źródeł. W tym przypadku za najlepsze oszacowanie przyjmuje się najmniejszy przedział zgodny z największą liczbą źródeł.

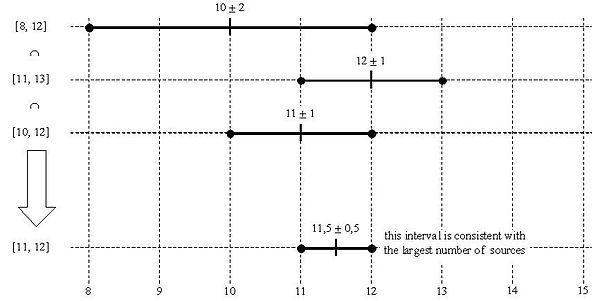
Jeśli mamy oszacowania 10 ± 2, 12 ± 1 i 11 ± 1, to te przedziały to [8,12], [11,13] i [10,12], które przecinają się, tworząc [11,12] lub 11,5 ± 0,5 jako zgodne ze wszystkimi trzema wartościami.

Jeśli zamiast tego zakresy to [8,12], [11,13] i [14,15], to nie ma przedziału zgodnego ze wszystkimi tymi wartościami, ale [11,12] jest zgodne z największą liczbą źródeł — mianowicie dwoma z nich.

Wreszcie, jeśli zakresy to [8,9], [8,12] i [10,12], to oba przedziały [8,9] i [10,12] są zgodne z największą liczbą źródeł.

Ta procedura określa interwał. Jeśli pożądanym wynikiem jest najlepsza wartość z tego przedziału, naiwnym podejściem byłoby przyjęcie środka przedziału jako wartości, co zostało określone w oryginalnym algorytmie Marzullo. Bardziej wyrafinowane podejście pozwoliłoby rozpoznać, że może to oznaczać odrzucanie użytecznych informacji z przedziałów ufności źródeł i że probabilistyczny model źródeł może zwrócić wartość inną niż środek.

Należy zauważyć, że obliczona wartość jest prawdopodobnie lepiej opisana jako „optymistyczna”, a nie „optymalna”. Rozważmy na przykład trzy przedziały [10,12], [11, 13] i [11,99,13]. Algorytm opisany poniżej oblicza [11,99, 12] lub 11,995 ± 0,005, co jest wartością bardzo precyzyjną. Jeśli podejrzewamy, że jedno z oszacowań może być błędne, to co najmniej dwa oszacowania muszą być poprawne. W tych warunkach najlepszym oszacowaniem jest [11,13], ponieważ jest to największy przedział, który zawsze przecina co najmniej dwa oszacowania. Algorytm opisany poniżej można łatwo sparametryzować z maksymalną liczbą błędnych oszacowań.

metoda

Algorytm Marzullo rozpoczyna się od przygotowania tabeli źródeł, posortowania jej, a następnie (efektywnego) wyszukania przecięć przedziałów. Dla każdego źródła istnieje przedział [c−r,c+r] określony przez c ± r. Dla każdego zakresu tabela będzie miała dwie krotki w postaci ⟨offset,type⟩. Jedna krotka będzie reprezentować początek zakresu, oznaczony typem −1 jako ⟨c−r,−1⟩, a druga będzie reprezentować koniec zakresu typem +1 jako ⟨c+r,+1⟩.

W opisie algorytmu wykorzystywane są zmienne: best (największa liczba znalezionych nachodzących na siebie interwałów), cnt (bieżąca liczba nachodzących na siebie interwałów), beststart i bestend (początek i koniec najlepszego dotychczas znalezionego interwału), i (indeks) i tabela krotek.

0. Zbuduj tabelę krotek.
1. Posortuj tabelę według przesunięcia. (Jeśli istnieją dwie krotki o tym samym przesunięciu, ale przeciwnych typach, wskazujące, że jeden interwał kończy się tak samo, jak zaczyna się inny, wówczas konieczna jest metoda decydowania, która z nich jest pierwsza. Takie zdarzenie można uznać za nakładanie się bez czasu trwania, które można znaleźć przez algorytm, umieszczając typ -1 przed typem + 1. Jeśli takie patologiczne nakładanie się zostanie uznane za niewłaściwe, można ich uniknąć, umieszczając w tym przypadku typ +1 przed -1.)
2. [inicjalizuj] best=0 cnt=0
3. [pętla] przechodzi przez każdą krotkę w tabeli w porządku rosnącym

4. [bieżąca liczba nakładających się przedziałów] cnt=cnt−type[i]
5. jeśli cnt>najlepiej, to najlepiej=cnt beststart=offset[i] bestend=offset[i+1]

komentarz: następna krotka w [i+1] będzie albo końcem przedziału (typ=+1) i wtedy zakończy ten najlepszy przedział, albo będzie początkiem przedziału (typ=−1 ) iw następnym kroku zastąpi najlepsze.

dwuznaczność: nieokreślona jest to, co zrobić, jeśli best=cnt. Jest to warunek remisu dla największego nakładania się. Można podjąć decyzję o wybraniu mniejszego spośród bestend-beststart i offset[i+1]-offset[i] lub po prostu wybrać dowolny z dwóch równie dobrych wpisów. Ta decyzja jest istotna tylko wtedy, gdy type[i+1]=+1.

6. [końcowa pętla] zwraca [beststart,bestend] jako optymalny interwał. Liczba fałszywych źródła (które nie pokrywają się zwróconego przedziału optymalnego) to liczba źródeł pomniejszona o wartość najlepszego.

Efektywność

Algorytm Marzullo jest wydajny zarówno w czasie, jak iw przestrzeni. Asymptotyczne wykorzystanie przestrzeni to O(n) , gdzie n to liczba źródeł. Rozważając asymptotyczne wymagania czasowe, można uznać, że algorytm polega na budowaniu tablicy, sortowaniu jej i przeszukiwaniu. Sortowanie można przeprowadzić w czasie O(n log n), co dominuje w fazach budowy i wyszukiwania, które można przeprowadzić w liniowym . Dlatego efektywność czasowa algorytmu Marzullo wynosi O(n log n) .

Po zbudowaniu i posortowaniu tablicy istnieje możliwość aktualizacji interwału dla jednego źródła (po otrzymaniu nowych informacji) w czasie liniowym. W związku z tym aktualizacja danych dla jednego źródła i znalezienie najlepszego interwału może odbywać się w czasie O(n).

•    Marzullo, KA (luty 1984). Utrzymywanie czasu w systemie rozproszonym: przykład luźno powiązanej usługi rozproszonej . doktorat rozprawa (rozprawa). Departament inżynierii elektrycznej. Uniwersytet Stanford. ASIN B000710CSC . OCLC 38621764 . DDC 3781.1984 M.

Linki zewnętrzne

• Mills, David L. (5 sierpnia 2000). „Krótka historia czasu NTP: wyznania internetowego chronometrażysty” (PDF) . EECIS . UDEL.
• „Keith Marzullo” . CSE . UCSD.