Spokojne skrzyżowanie

Zrelaksowane przecięcie m zbiorów odpowiada klasycznemu przecięciu między zbiorami, z tą różnicą , że można rozluźnić kilka zbiorów, aby uniknąć pustego przecięcia. Pojęcie to można zastosować do rozwiązywania problemów z spełnianiem ograniczeń , które są niespójne, poprzez złagodzenie niewielkiej liczby ograniczeń . Kiedy estymacji parametrów rozważane jest podejście z ograniczonym błędem , rozluźnione przecięcie umożliwia odporność na niektóre wartości odstające .

Definicja

q -zrelaksowane przecięcie m podzbiorów $}$ oznaczone przez ${1}, \ kropki, X_$${\ Displaystyle X ^ {\ {q \}} = \ bigcap ^ {\ {q \}} X_ {i}} jest$ \ displaystyle { zbiorem wszystkich ${\ displaystyle x\ w R^{n}}$ , które należą do wszystkich ${\ displaystyle X_ {i}}$ , z wyjątkiem $najwyżej$ . Definicję tę ilustruje rysunek 1.

Rysunek 1. q - przecięcie 6 zbiorów dla q =2 (czerwony), q =3 (zielony), q = 4 (niebieski), q = 5 (żółty).

Zdefiniuj ${\ Displaystyle \ lambda (x) = {\ tekst {karta}} \ lewo \ {i \ |\ x \ w X_ {i} \ prawo \}.}$

Mamy ${\ Displaystyle X ^ {\ {q \}} = \ lambda ^ {- 1} ([mq, m]).}$

Charakteryzowanie przecięcia q-zrelaksowanego jest zatem problemem inwersji zbiorów .

Przykład

Rozważ 8 przedziałów: ${\ Displaystyle X_ {1} = [1,4],}$${\ Displaystyle X_ {2} = \ [2,4 ],}$${\ Displaystyle X_ {3} = [2,7],}$${\ Displaystyle X_ {4} = [6,9], }$ ${\ Displaystyle X_ {5} = [3,4],}$${\ displaystyle X_ {6} = [3,7].}$

Mamy

${\ Displaystyle X ^ {\ {0 \}} = \ pusty zestaw,}$${\ Displaystyle X ^ {\ {1 \}} = [3, 4],}$${\ Displaystyle X ^ {\ {2 \}} = [3,4],}$ ${\ Displaystyle X ^ {\ {3 \}} = [2,4] \ Puchar [6,7],}$${\ Displaystyle X ^ {\ {4 \ }} = [2,7],}$${\ Displaystyle X ^ {\ {5 \}} = [1,9],}$${\ Displaystyle X ^ {\ {6 \}} =] - \ infty, \ infty [.}$

Spokojne przecięcie interwałów

Zrelaksowane przecięcie interwałów nie jest koniecznym interwałem. W ten sposób bierzemy kadłub interwałowy wyniku. Jeśli $obliczyć$ ze złożonością m .log ( ) pomocą algorytmu Marzullo . $przedstawić$ posortować wszystkie dolne i górne granice m przedziałów, aby funkcję . Wtedy bez problemu otrzymamy komplet

${\ Displaystyle X ^ {\ {q \}} = \ lambda ^ {- 1} ([mq, m])}$

co odpowiada sumie przedziałów. Następnie zwracamy najmniejszy przedział zawierający tę sumę.

$.$ funkcję poprzednim przykładem

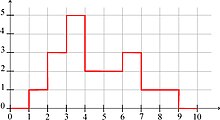
Rysunek 2. Funkcja przynależności do zbioru powiązana z 6 przedziałami.

Zrelaksowane skrzyżowanie pudełek

Aby obliczyć $q$ -zrelaksowane przecięcie m pudełek , rzutujemy wszystkie pudełek względem n osi Dla każdej z n grup m przedziałów obliczamy przecięcie q -zrelaksowane. Zwracamy iloczyn kartezjański n wynikowych przedziałów. Rysunek 3 przedstawia ilustrację 4-zrelaksowanego przecięcia 6 pudełek. Każdy punkt czerwonego pola należy do 4 z 6 pól.

Rysunek 3. Czerwona ramka odpowiada 4-zrelaksowanemu przecięciu 6 ramek

Zrelaksowana Unia

q -zrelaksowany związek $\ kropki, X_ {m}}$ X_ {1} ,

${\ Displaystyle {\ overset {\ {q \}} {\ bigcup}} X_ {i} = \ bigcap ^ {\ {m-1- q\}}X_{i}}$

Należy zauważyć, że gdy q =0, rozluźniony związek/przecięcie odpowiada klasycznemu złączu/przecięciu. Dokładniej, mamy

${\ Displaystyle \ bigcap ^ {\ {0 \}} X_ {i} = \ bigcap X_ {i}}$

I

${\ Displaystyle {\ overset {\ {0 \}} {\ bigcup}} X_ {i} = \ bigcup X_ {i}}$

Prawo De Morgana

Jeśli oznacza komplementarny zbiór , mamy $\$$displaystyle {\ overline {X}$

${\ Displaystyle {\ overline {\ bigcap ^ {\ {q \}} X_ {i}}} = {\ overset {\ {q \}} \bigcup }}{\overline {X_{i}}}}$

${\ Displaystyle {\ overline {{\ overset {\ {q \}} {\ bigcup}} X_ {i}} = \ bigcap ^ {\ {q \}} {\ overline {X_ {i}}}. }$

W konsekwencji

${\ Displaystyle {\ overline {\ bigcap \ granice ^ {\ {q \}} X_{i}}}={\overline {{\overset {\{mq-1\}}{\bigcup }}X_{i}}}=\bigcap ^{\{mq-1\}}{\overline {X_{i}}}}$

Odprężenie wykonawców

Niech $\ displaystyle C_ {1}, \ kropek, C_ {m}}$ będą m wykonawcami zbiorów ${\ displaystyle X_ {1}, \ kropek, X_ { m}}$ , następnie

${\ Displaystyle C ([x]) = \ bigcap ^ {\ {q \}} C_ {i} ([x]).}$

jest wykonawcą dla i . ${\ displaystyle X ^ {\ {q \}}}$

${\ Displaystyle {\ overline {C}} ([x]) = \ bigcap ^ {\ {mq-1 \ }}{\overline {C}}_{i}([x])}$

jest wykonawcą dla , gdzie ${\ displaystyle {\ overline {X}} ^ {\ {q \}}}$

${\ Displaystyle {\ overline {C}} _ ​​{1}, \ kropki, {\ overline {C}} _ ​​{m}}$

są wykonawcami

${\ Displaystyle {\ overline {X}} _ {1}, \ kropki, {\ overline {X}} _ {m}.}$

W połączeniu z algorytmem rozgałęzionym, $takim$ jak SIVIA (Inwersja zbiorów poprzez przedziałową), można obliczyć q -zrelaksowane przecięcie m podzbiorów zbioru

Zastosowanie do estymacji błędów ograniczonych

Przecięcie q -zrelaksowane można wykorzystać do niezawodnej lokalizacji lub śledzenia.

Odpornych obserwatorów można również wdrożyć przy użyciu rozluźnionych przecięć, aby byli odporni na wartości odstające.

Proponujemy tutaj prosty przykład ilustrujący tę metodę. Rozważmy model, którego i- ty wynik modelu jest dany przez

${\ Displaystyle f_ {i} (p) = {\ Frac {1} {\ sqrt {2 \ pi p_{2}}}}\exp(-{\frac {(t_{i}-p_{1})^{2}}{2p_{2}}})}$

gdzie ${\ Displaystyle p \ w R ^ {2}$ } Załóżmy, że tak

${\ Displaystyle f_ {i} (p) \ w [y_ {i}]}$

gdzie ${\ displaystyle t_ {i}}$ i ${\ displaystyle [y_ {i}]}$ są podane na poniższej liście

${\ Displaystyle \ {(1, [0; 0,2]), (2, [0,3; 2]), (3, [0,3; 2]), (4, [0,1; 0,2]), ( 5,[0,4;2]),(6,[-1;0,1])\}}$

Zestawy dla różnych $}$ na rysunku 4. ${\ displaystyle \ lambda ^ {- 1} (q)$

Rysunek 4. Zbiór wszystkich wektorów parametrów zgodnych z dokładnie 6-q słupkami danych (pomalowanymi na czerwono), dla q=1,2,3,4,5.