Ciężki materiał fermionowy

W fizyce ciała stałego ciężkie materiały fermionowe są szczególnym rodzajem związków międzymetalicznych , zawierających pierwiastki z elektronami 4f lub 5f w niewypełnionych pasmach elektronowych . Elektrony są jednym z rodzajów fermionów , a kiedy znajdują się w takich materiałach, są czasami określane jako ciężkie elektrony . Ciężkie materiały fermionowe mają ciepło właściwe w niskiej temperaturze, którego wyraz liniowy jest do 1000 razy większy niż wartość oczekiwana z modelu elektronów swobodnych . Właściwości ciężkich związków fermionowych często wynikają z częściowo wypełnionych orbitali f metali ziem rzadkich lub aktynowców , które zachowują się jak zlokalizowane momenty magnetyczne . Nazwa „ciężki fermion” pochodzi od faktu, że fermion zachowuje się tak, jakby miał masę efektywną większą niż jego masa spoczynkowa. W przypadku elektronów, poniżej charakterystycznej temperatury (zwykle 10 K), elektrony przewodnictwa w tych związkach metali zachowują się tak, jakby miały efektywną masę do 1000 razy większą od cząstki swobodnej masa. Ta duża masa efektywna znajduje również odzwierciedlenie w dużym udziale w rezystywności rozpraszania elektron-elektron poprzez stosunek Kadowakiego – Woodsa . Zachowanie ciężkich fermionów stwierdzono w wielu różnych stanach, w tym w stanach metalicznych, nadprzewodzących , izolujących i magnetycznych. Charakterystycznymi przykładami są CeCu ₆ , CeAl ₃ , CeCu ₂ Si ₂ , YbAl ₃ , UBe ₁₃ i UPt ₃ .

Przegląd Historyczny

Zachowanie ciężkich fermionów zostało odkryte przez K. Andresa, JE Graebnera i HR Otta w 1975 r., którzy zaobserwowali ogromne wielkości liniowego ciepła właściwego w CeAl ₃ .

Podczas gdy badania domieszkowanych nadprzewodników doprowadziły do wniosku, że istnienie zlokalizowanych momentów magnetycznych i nadprzewodnictwa w jednym materiale jest niekompatybilne, wykazano coś przeciwnego, kiedy w 1979 roku Frank Steglich i in. odkrył nadprzewodnictwo ciężkiego fermionu w materiale CeCu ₂ Si ₂ .

Odkrycie kwantowego punktu krytycznego i zachowania cieczy innej niż Fermi na diagramie fazowym ciężkich związków fermionowych przez H. von Löhneysena i in. w 1994 roku spowodowały nowy wzrost zainteresowania badaniami tych związków. Kolejnym eksperymentalnym przełomem było wykazanie (przez grupę Gila Lonzaricha ), że krytyczność kwantowa w ciężkich fermionach może być przyczyną niekonwencjonalnego nadprzewodnictwa.

Ciężkie materiały fermionowe odgrywają ważną rolę w bieżących badaniach naukowych, działając jako prototypowe materiały do niekonwencjonalnego nadprzewodnictwa, zachowania cieczy innych niż Fermi i krytyczności kwantowej. Rzeczywista interakcja między zlokalizowanymi momentami magnetycznymi a elektronami przewodzącymi w ciężkich związkach fermionowych wciąż nie jest w pełni poznana i jest przedmiotem trwających badań.

Nieruchomości

Ciężkie materiały fermionowe należą do grupy silnie skorelowanych układów elektronowych .

Kilku członków grupy ciężkich materiałów fermionowych staje się nadprzewodnikami poniżej temperatury krytycznej. Nadprzewodnictwo jest niekonwencjonalne .

W wysokich temperaturach ciężkie związki fermionowe zachowują się jak normalne metale, a elektrony można opisać jako gaz Fermiego , w którym przyjmuje się, że elektrony są nieoddziałującymi fermionami. W tym przypadku można pominąć interakcję między elektronami f , które mają lokalny moment magnetyczny, a elektronami przewodzącymi.

Teoria cieczy Fermiego Leva Landaua zapewnia dobry model opisujący właściwości większości ciężkich materiałów fermionowych w niskich temperaturach. W tej teorii elektrony opisywane są kwazicząstkami , które mają takie same liczby kwantowe i ładunek, ale oddziaływanie elektronów uwzględnia się wprowadzając masę efektywną , która różni się od rzeczywistej masy swobodnego elektronu.

Właściwości optyczne

Typowe przewodnictwo optyczne zależne od częstotliwości ciężkiego związku fermionowego. Niebieska linia: T > T _coh . Czerwona linia: T < T _coh .

W celu uzyskania właściwości optycznych ciężkich układów fermionowych materiały te zostały zbadane za pomocą pomiarów spektroskopii optycznej . W tych eksperymentach próbka jest naświetlana falami elektromagnetycznymi o regulowanej długości fali . Pomiar odbitego lub przechodzącego światła ujawnia charakterystyczne energie próbki.

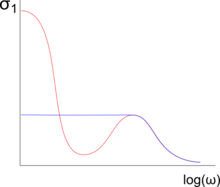
Powyżej charakterystycznej temperatury koherencji $jak$ materiały fermionowe zachowują się tj. ich odpowiedź optyczna jest opisana przez model Drude'a . Jednak w porównaniu z dobrym metalem, ciężkie związki fermionów w wysokich temperaturach mają wysoki współczynnik rozpraszania ze względu na dużą gęstość lokalnych momentów magnetycznych (co najmniej jeden elektron f na komórkę elementarną), które powodują (niespójne) Kondo rozpraszanie. Ze względu na dużą szybkość rozpraszania, przewodność prądu stałego i przy niskich częstotliwościach jest raczej niska. Spadek przewodnictwa (spadek Drude'a) występuje przy częstotliwości odpowiadającej szybkości relaksacji.

Poniżej $hybrydyzują$ elektrony f . Prowadzi to do zwiększonej masy efektywnej i rozwija się luka hybrydyzacyjna. W przeciwieństwie do izolatorów Kondo , potencjał chemiczny ciężkich związków fermionowych leży w paśmie przewodnictwa. Zmiany te prowadzą do dwóch ważnych cech w odpowiedzi optycznej ciężkich fermionów.

Zależną od częstotliwości przewodność materiałów ciężkich fermionów można wyrazić wzorem ${\ Displaystyle \ sigma (\ omega) = {\ Frac {ne ^ { 2}}{m^{*}}}{\frac {\tau ^{*}}{1+\omega ^{2}\tau ^{*2}}}} , zawierające efektywną masę$ m $\ styl wyświetlania m^{*}}$ i renormalizowana szybkość relaksacji ${\ Displaystyle {\ Frac {1} {\ tau ^ {*}}} = {\ Frac {m} {m ^ {*}}} {\ Frac {1} {\ tau}}}$ . Ze względu na dużą masę efektywną, renormalizowany czas relaksacji jest również zwiększony, co prowadzi do wąskiego spadku Drude'a przy bardzo niskich częstotliwościach w porównaniu do zwykłych metali. Najniższą taką szybkość relaksacji Drude'a obserwowaną dotychczas w ciężkich fermionach, w zakresie niskich GHz , stwierdzono w UPd ₂ Al ₃ .

Cecha podobna do przerwy w przewodnictwie optycznym reprezentuje bezpośrednio przerwę hybrydyzacyjną, która otwiera się w wyniku interakcji zlokalizowanych elektronów f i elektronów przewodzących. Ponieważ przewodnictwo nie zanika całkowicie, obserwowana przerwa jest w rzeczywistości pseudoprzerwą . Przy jeszcze wyższych częstotliwościach możemy zaobserwować lokalne maksimum przewodności optycznej spowodowane normalnymi wzbudzeniami międzypasmowymi.

Pojemność cieplna

Ciepło właściwe dla normalnych metali

W niskiej temperaturze i dla normalnych metali ciepło właściwe składa się z ciepła właściwego elektronów do $Displaystyle$ $\ rm {el}}}}$ która zależy liniowo od temperatury $}$ ciepła właściwego drgań sieci krystalicznej ( ${\ Displaystyle C_ {P, {\ rm {ph}}}},$ ) do która zależy sześciennie od temperatury T {\

{\ Displaystyle C_ {P} = C_ {P, {\ rm {el}}} + C_ {P, {\ rm { ph}}}=\gamma T+\beta T^{3}\ }

ze stałymi proporcjonalności i $displaystyle$ $\ gamma}$ .

We wspomnianym zakresie temperatur wkład elektroniczny stanowi większą część ciepła właściwego. W modelu swobodnych elektronów — prostym systemie modelowym, który pomija interakcję elektronów — lub metali, które można by nim opisać, ciepło właściwe elektronu jest wyrażone wzorem

\ Displaystyle C_ {P, {\ rm {el}}} = \ gamma T = {\ Frac {\ pi ^

ze stałą $,$ $najwyższą$ elektronów i Fermiego $_$ _ energia pojedynczej cząstki zajętych stanów elektronowych). $.$ proporcjonalności nazywana jest współczynnikiem Sommerfelda

Zależność między pojemnością cieplną a „efektywną masą termiczną”

Dla elektronów o kwadratowym stosunku dyspersji (jak dla gazu swobodnych elektronów) energia Fermiego ε _F jest odwrotnie proporcjonalna do masy cząstki m :

{\ Displaystyle \ epsilon _ {\ rm {F}} = {\ Frac {\ hbar ^ {2} k_ {\ rm {F}} ^ {2}} {2m} }}

gdzie oznacza liczbę falową Fermiego, która zależy od gęstości elektronów $jest wartością$ liczby falowej najwyższego zajętego stanu elektronowego. Tak $}$ , ponieważ parametr Sommerfelda $,$ odwrotnie proporcjonalny do jest proporcjonalny do masy cząstki i dla wysokiej $\ Displaystyle \ gamma$ wartości ${\ displaystyle \ gamma}$ , metal zachowuje się jak gaz Fermiego, w którym elektrony przewodzące mają wysoką termiczną masę efektywną.

Przykład: UBe ₁₃ w niskich temperaturach

Wyniki eksperymentalne dotyczące ciepła właściwego związku ciężkiego fermionu UBe ₁₃ pokazują pik w temperaturze około 0,75 K, który spada do zera z dużym nachyleniem, jeśli temperatura zbliża się do 0 K. Ze względu na ten pik, γ {\ displaystyle $gamma }$ jest znacznie wyższy niż w modelu elektronów swobodnych w tym zakresie temperatur. Natomiast powyżej 6 K ciepło właściwe tego ciężkiego fermionu zbliża się do wartości oczekiwanej z teorii swobodnych elektronów.

Krytyczność kwantowa

Obecność lokalnego momentu i zdelokalizowanych elektronów przewodzących prowadzi do współzawodnictwa oddziaływania Kondo (które faworyzuje niemagnetyczny stan podstawowy) i oddziaływania RKKY (które generuje stany uporządkowane magnetycznie, zazwyczaj antyferromagnetyczne dla ciężkich fermionów). Tłumiąc temperaturę Néela antyferromagnesu ciężkiego fermionu do zera (np. przez przyłożenie ciśnienia lub pola magnetycznego lub poprzez zmianę składu materiału), kwantowe przejście fazowe można wywołać. W przypadku kilku ciężkich materiałów fermionowych wykazano, że takie kwantowe przejście fazowe może generować bardzo wyraźne właściwości cieczy innych niż Fermi w skończonych temperaturach. Takie kwantowo-krytyczne zachowanie jest również szczegółowo badane w kontekście niekonwencjonalnego nadprzewodnictwa .

Przykładami ciężkich fermionów o dobrze zbadanych właściwościach krytycznych kwantowo są CeCu _6−x Au, CeIn ₃ , CePd ₂ Si ₂ , YbRh ₂ Si ₂ i CeCoIn ₅ .

Niektóre ciężkie związki fermionowe

Dalsza lektura

Kittel, Charles (1996) Wprowadzenie do fizyki ciała stałego , wyd. 7, John Wiley and Sons, Inc.
Marder, MP (2000), Condensed Matter Physics, John Wiley & Sons, Nowy Jork.
Hewson, AC (1993), The Kondo Problem to Heavy Fermions, Cambridge University Press.
Fulde, P. (1995), Electron Correlations in Molecules and Solids, Springer, Berlin.
Amusia, M., Popov, K., Shaginyan, V., Stephanovich, V. (2015). Teoria ciężkich związków fermionowych - Teoria silnie skorelowanych systemów Fermiego . Seria Springera w naukach o ciele stałym. Tom. 182. Springera. doi : 10.1007/978-3-319-10825-4 . ISBN 978-3-319-10824-7 . {{ cite book }} : CS1 maint: wiele nazwisk: lista autorów ( link )