Dwudziestościan Pentakisa

Dwudziestościan Pentakisa
Pentakis icosidodecahedron.png
Typ Wielościan geodezyjny (2,0)
Twarze
80 trójkątów (20 równobocznych ; 60 równoramiennych )
Krawędzie 120 (2 rodzaje)
Wierzchołki 42 (2 rodzaje)
Konfiguracja wierzchołków
(12) 3 5 (30) 3 6
Notacja Conwaya k5aD = dcD = uI
Grupa symetrii Dwudziestościan ( I h )
Podwójny wielościan Fazowany dwunastościan
Nieruchomości wypukły
Internet
Pentakis icosidodecahedron net.png

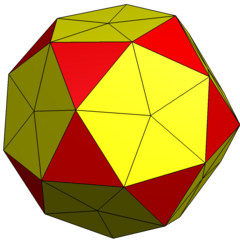
W geometrii pentakis dwudziestościan lub podzielony dwudziestościan jest wypukłym wielościanem z 80 trójkątnymi ścianami , 120 krawędziami i 42 wierzchołkami . Jest to podwójny rombowy triacontahedron ( dwunastościan fazowany ).

Budowa

Jego nazwa pochodzi od konstrukcji topologicznej dwudziestościanu z operatorem kis zastosowanym do ścian pięciokątnych. W tej konstrukcji zakłada się, że wszystkie wierzchołki znajdują się w tej samej odległości od środka, podczas gdy ogólnie symetria dwudziestościanu może być zachowana nawet przy 12 wierzchołkach rzędu 5 w innej odległości od środka niż pozostałe 30.

Można go również zbudować topologicznie z dwudziestościanu , dzieląc każdą trójkątną ścianę na 4 trójkąty, dodając wierzchołki środkowej krawędzi. Z tej konstrukcji wszystkie 80 trójkątów będzie równobocznych, ale twarze będą współpłaszczyznowe .

Conway (u 2 ) I (k5)aI
Obraz Icosahedron subdivided.png Conway polyhedron flat k5aI.png
Formularz Dwudziestościan podzielony na 2 częstotliwości Dwudziestościan Pentakisa

Powiązane wielościany

  • Pentakis dodecahedron is a slightly smaller Catalan solid which has 60 isosceles triangle faces, 90 edges (2 types), and 32 vertices (2 types).

    Pentakis dwunastościan to nieco mniejsza bryła katalońska , która ma 60 ścian trójkąta równoramiennego, 90 krawędzi (2 typy) i 32 wierzchołki (2 typy).

  • Tripentakis icosidodecahedron, the Kleetope of the icosidodecahedron, can be obtained by raising low pyramids on each equilateral triangular face on a pentakis icosidodecahedron. It has 120 isosceles triangle faces (2 types), 180 edges (3 types) and 62 vertices (3 types).

    Tripentakis icosidodecahedron, Kleetope dwudziestościanu dwudziestościanu, można uzyskać, wznosząc niskie piramidy na każdej trójkątnej ścianie równobocznej na pentakis dwudziestościanu. Ma 120 trójkątów równoramiennych (2 typy), 180 krawędzi (3 typy) i 62 wierzchołki (3 typy).

  • The nonconvex small icosihemidodecahedron looks like a pentakis icosidodecahedron with inverted pentagonal pyramids meeting at the polyhedron center.

    Niewypukły mały dwudziestościan wygląda jak dwudziestościan pentakis z odwróconymi pięciokątnymi piramidami spotykającymi się w środku wielościanu.

Powiązane polytopy

Reprezentuje zewnętrzną obwiednię prostopadłej projekcji 600-komorowej wyśrodkowanej na wierzchołkach , jednej z sześciu wypukłych regularnych 4-polytopów , w 3 wymiarach.

Zobacz też

  • George W. Hart , Rzeźba oparta na wielościanach napędowych , Proceedings of MOSAIC 2000, Seattle, WA, sierpień 2000, s. 61–70 [1]
  •   John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
    • Rozdział 21: Nazewnictwo wielościanów archimedesowych i katalońskich oraz Tilings (s. 284)
  •     Wenninger, Magnus (1979), modele sferyczne , Cambridge University Press , ISBN 978-0-521-29432-4 , MR 0552023 Dover 1999 ISBN 978-0-486-40921-4

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Pentakis_icosidodecahedron&oldid=1093695085 ”