Fale jagnięce

Fale jagnięce rozchodzą się w pełnych płytach lub kulach. Są to fale sprężyste , których ruch cząstek leży w płaszczyźnie zawierającej kierunek rozchodzenia się fali i kierunek prostopadły do płyty. W 1917 roku angielski matematyk Horace Lamb opublikował swoją klasyczną analizę i opis fal akustycznych tego typu. Ich właściwości okazały się dość złożone. Nieskończony ośrodek obsługuje tylko dwa tryby fal poruszające się z unikalnymi prędkościami; ale płyty obsługują dwa nieskończone zestawy modów fal Lamb, których prędkości zależą od związku między długością fali a grubością płyty.

Od lat 90. zrozumienie i wykorzystanie fal Lamb znacznie się rozwinęło dzięki szybkiemu wzrostowi dostępności mocy obliczeniowej. Teoretyczne sformułowania Lamba znalazły praktyczne zastosowanie, zwłaszcza w dziedzinie badań nieniszczących.

Termin fale Rayleigha-Lamba obejmuje falę Rayleigha , rodzaj fali, która rozchodzi się wzdłuż jednej powierzchni. Zarówno fale Rayleigha, jak i Lamba są ograniczone przez sprężyste właściwości powierzchni (powierzchni), które nimi kierują.

₀
₀
Rysunek 1: odpowiednio górny i dolny: tryb ekstensjonalny ( S ) z

{\ Displaystyle d / \ lambda = 0,6}

. Tryb zginania (A ) z

{\ Displaystyle d / \ lambda = 0,3}

. (To jest uproszczona grafika. Opiera się tylko na składowej ruchu Z , więc nie oddaje dokładnie zniekształcenia płyty.)

Równania charakterystyczne Lamba

Ogólnie rzecz biorąc, fale sprężyste w materiałach stałych są kierowane przez granice ośrodków, w których się rozchodzą. Podejście do propagacji fal kierowanych, szeroko stosowane w akustyce fizycznej, polega na poszukiwaniu sinusoidalnych rozwiązań równania falowego dla liniowych fal sprężystych podlegających warunkom brzegowym reprezentującym geometrię strukturalną. Jest to klasyczny z wartością własną .

Fale w płytach były jednymi z pierwszych fal kierowanych analizowanych w ten sposób. Analiza została opracowana i opublikowana w 1917 roku przez Horace'a Lamba , ówczesnego lidera fizyki matematycznej.

Równania Lamba zostały wyprowadzone przez utworzenie formalizmu dla litej płyty o nieskończonej rozpiętości w kierunkach x i y oraz grubości d w kierunku z . Postulowano sinusoidalne rozwiązania równania falowego o przesunięciach postaci x i z

{\ Displaystyle \ xi = A_ {x} f_ {x} (z) e ^ {i (\ omega t-kx)} \quad \quad (1)}

{\ Displaystyle \ zeta = A_ {z} f_ {z} (z) e ^ {i (\ omega t-kx)} \ quad \ quad (2)}

Postać ta reprezentuje fale sinusoidalne rozchodzące się w kierunku x o długości fali 2π/k i częstotliwości ω/2π. Przemieszczenie jest funkcją x , z , t ; nie ma przesunięcia w y ani zmiany jakichkolwiek wielkości fizycznych w kierunku y .

Fizycznym warunkiem brzegowym dla swobodnych powierzchni płyty jest to, że składowa naprężenia w kierunku z w punkcie z = +/- d /2 wynosi zero. Stosując te dwa warunki do wyżej sformalizowanych rozwiązań równania falowego, można znaleźć parę charakterystycznych równań. To są:

{\ Displaystyle {\ Frac {\ tanh (\ beta d/2)} {\tanh(\alpha d/2)}}={\frac {4\alpha \beta k^{2}}{(k^{2}+\beta ^{2})^{2}}}\ \quad \quad \quad \quad (3)}

dla modów symetrycznych i

{\ Displaystyle {\ Frac {\ tanh (\ beta d/2)} {\tanh(\alpha d/2)}}={\frac {(k^{2}+\beta ^{2})^{2}}{4\alpha \beta k^{2}}}\ \quad \quad \quad \quad (4)}

dla modów asymetrycznych, gdzie

{\ Displaystyle \ alfa ^ {2} = k ^ {2} - {\ Frac {\ omega ^ {2}} {c_ {l} ^ {2}}} \ quad \ quad {\ tekst {i}} \ quad \quad \beta ^{2}=k^{2}-{\frac {\omega ^{2}}{c_{t}^{2}}}.}

Nieodłącznym elementem tych równań jest zależność między częstotliwością kątową ω a liczbą falową k. Do znalezienia prędkości fazowej _fd cp = fλ = ω/k i prędkości grupowej c _g = dω / dk , jako funkcji d / λ lub , stosuje się metody numeryczne . c _l i c _t to odpowiednio prędkości fali podłużnej i poprzecznej .

Rozwiązanie tych równań ujawnia również dokładną postać ruchu cząstki, którą równania (1) i (2) przedstawiają jedynie w postaci ogólnej. Stwierdzono, że równanie (3) daje początek rodzinie fal, których ruch jest symetryczny względem płaszczyzny środkowej płyty (płaszczyźnie z = 0), podczas gdy równanie (4) daje początek rodzinie fal, których ruch jest antysymetryczny wokół płaszczyzna środkowa. Rycina 1 przedstawia członka każdej rodziny.

Równania charakterystyczne Lamba zostały ustalone dla fal rozchodzących się w nieskończonej płycie - jednorodnej, izotropowej bryle ograniczonej dwiema równoległymi płaszczyznami, poza którymi energia fal nie może się rozchodzić. Formułując swój problem, Lamb ograniczył składowe ruchu cząstek do kierunku normalnej płyty ( z ) i kierunku rozchodzenia się fali ( kierunek x ). Z definicji fale Lamb nie mają ruchu cząstek w kierunku y . Ruch w y w płytach występuje w tak zwanych trybach SH lub poziomej fali ścinającej. Te nie mają ruchu w x - lub z -kierunki, a zatem są uzupełnieniem trybów fali Lamb. Te dwa są jedynymi typami fal, które mogą rozchodzić się z prostymi, nieskończonymi czołami fal w płycie, jak zdefiniowano powyżej.

Dyspersja prędkości zawarta w równaniach charakterystycznych

Krzywe dyspersji swobodnych fal Lamba dla dwóch różnych współczynników Poissona

{\ displaystyle \ sigma}

. Oś

przez

przedstawia

iloczyn częstotliwości kątowej grubości płyty

prędkość

ścinającej . Oś y pokazuje prędkość fazową

.

Lamba znormalizowaną przez prędkość fali poprzecznej Dla wysokich częstotliwości i

{\ displaystyle S_ {0}}

Rayleigha

, około 92% prędkości fali poprzecznej.

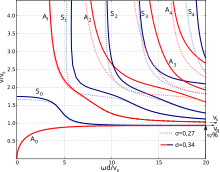
Fale jagnięce wykazują dyspersję prędkości; to znaczy ich prędkość propagacji c zależy od częstotliwości (lub długości fali), a także od stałych sprężystości i gęstości materiału. Zjawisko to ma kluczowe znaczenie dla badania i zrozumienia zachowania fal w płytach. Fizycznie kluczowym parametrem jest stosunek grubości płyty d do $fali$ . Ten stosunek określa efektywną sztywność płyty, a tym samym prędkość fali. W zastosowaniach technologicznych stosuje się bardziej praktyczny parametr, który łatwo z tego wyprowadzić, a mianowicie iloczyn grubości i częstotliwości:

{\ Displaystyle f \ cdot d = {\ Frac {d \ cdot c} {\ lambda}}}

ponieważ dla wszystkich fal

{\ displaystyle c = f \ lambda.}

Zależność między prędkością a częstotliwością (lub długością fali) jest nieodłącznym elementem charakterystycznych równań. W przypadku płytki równania te nie są proste, a ich rozwiązanie wymaga metod numerycznych. Był to nierozwiązywalny problem aż do pojawienia się komputera cyfrowego czterdzieści lat po oryginalnej pracy Lamb. Publikacja wygenerowanych komputerowo „krzywych dyspersji” przez Viktorova w byłym Związku Radzieckim, Firestone'a, a następnie Worltona w Stanach Zjednoczonych i ostatecznie wielu innych, wprowadziła teorię fal Lamba do sfery praktycznego zastosowania. Bezpłatne oprogramowanie „Kalkulator dyspersji” (DC) umożliwia obliczanie wykresów dyspersji dla płyt izotropowych i wielowarstwowych próbek anizotropowych. Eksperymentalne przebiegi obserwowane na płytkach można zrozumieć poprzez interpretację w odniesieniu do krzywych dyspersji.

Krzywe dyspersji – wykresy przedstawiające zależności między prędkością fali, długością fali i częstotliwością w układach dyspersyjnych – można przedstawić w różnych formach. Forma, która daje największy wgląd w podstawową fizykę, ma $)$ na osi y i k (liczbę fal na osi x . Forma użyta przez Viktorova, która wprowadziła fale Lamba do praktycznego użytku, ma prędkość fali na osi y i ${\ Displaystyle d / \ lambda}$ , stosunek grubości do długości fali na osi x . Najbardziej praktyczna ze wszystkich postaci, za którą zawdzięczamy J. i H. Krautkrämerów, jak również Floyda Firestone'a (który, nawiasem mówiąc, ukuł wyrażenie „fale jagnięcia”), ma prędkość fali na osi y i fd , iloczyn częstotliwości i grubości na osi x .

Charakterystyczne równania Lamba wskazują na istnienie dwóch całych rodzin modów fali sinusoidalnej w nieskończonych płytach $szerokości$ . Kontrastuje to z sytuacją w ośrodkach nieograniczonych, w których istnieją tylko dwa tryby fal, fala podłużna i fala poprzeczna lub poprzeczna . Podobnie jak w falach Rayleigha , które rozchodzą się wzdłuż pojedynczych swobodnych powierzchni, ruch cząstek w falach Lamba jest eliptyczny ze swoimi x i z elementy w zależności od głębokości w płycie. W jednej rodzinie modów ruch jest symetryczny względem płaszczyzny średniej grubości. W drugiej rodzinie jest antysymetryczny. Zjawisko dyspersji prędkości prowadzi do bogatej różnorodności obserwowalnych eksperymentalnie przebiegów fal akustycznych rozchodzących się w płytach. Jest to prędkość grupowa c _g , a nie wspomniana powyżej prędkość fazowa c lub c _p , który określa modulacje widoczne w obserwowanym przebiegu. Wygląd przebiegów zależy krytycznie od zakresu częstotliwości wybranego do obserwacji. Tryby zginania i rozciągania są stosunkowo łatwe do rozpoznania i zaleca się to jako technikę badań nieniszczących .

Tryby rzędu zerowego

Na szczególną uwagę zasługują symetryczne i antysymetryczne tryby zerowego rzędu. Tryby te mają „powstające częstotliwości” równe zero. Tak więc są to jedyne mody, które istnieją w całym spektrum częstotliwości od zera do nieskończenie wysokich częstotliwości. W zakresie niskich częstotliwości (tj. gdy długość fali jest większa niż grubość płyty) mody te są często nazywane odpowiednio „trybem rozciągania” i „modem zginania”. prędkości propagacji.Eliptyczny ruch cząstek odbywa się głównie w płaszczyźnie płyty dla trybu symetrycznego, ekstensyjnego i prostopadłego do płaszczyzny płyty dla trybu antysymetrycznego, giętnego.Charakterystyki te zmieniają się przy wyższych częstotliwościach.

Te dwa mody są najważniejsze, ponieważ (a) występują na wszystkich częstotliwościach i (b) w większości praktycznych sytuacji przenoszą więcej energii niż mody wyższego rzędu.

₀ Symetryczny mod zerowego rzędu (oznaczony S ) porusza się z „prędkością płyty” w reżimie niskich częstotliwości, gdzie jest właściwie nazywany „modem rozszerzonym”. W tym reżimie płyta rozciąga się w kierunku propagacji i odpowiednio kurczy się w kierunku grubości. Gdy częstotliwość wzrasta, a długość fali staje się porównywalna z grubością płyty, zakrzywienie płyty zaczyna mieć znaczący wpływ na jej efektywną sztywność. Prędkość fazowa spada płynnie, podczas gdy prędkość grupowa spada nieco gwałtownie w kierunku minimum. Jeszcze przy wyższych częstotliwościach zarówno prędkość fazowa, jak i prędkość grupowa zbiegają się w kierunku prędkości fali Rayleigha - prędkości fazowej z góry i prędkości grupowej z dołu.

W granicy niskiej częstotliwości dla trybu ekstensyjnego składowe z i x przemieszczenia powierzchniowego są kwadraturowe, a stosunek ich amplitud jest określony wzorem:

{\ Displaystyle {\ Frac {a_ {z}} {a_ {x}}} = {\ Frac {\ pi \ nu} {(1-\ nu)}}. {\ Frac {d} {\ lambda }}}

gdzie

jest

Poissona.

₀ Tryb antysymetryczny rzędu zerowego (oznaczony jako A ) jest wysoce dyspersyjny w reżimie niskich częstotliwości, gdzie jest właściwie nazywany „trybem zginania” lub „modem zginania”. W przypadku bardzo niskich częstotliwości (bardzo cienkie płytki) prędkości fazowe i grupowe są proporcjonalne do pierwiastka kwadratowego z częstotliwości; prędkość grupowa jest dwukrotnie większa od prędkości fazowej. Ta prosta zależność jest konsekwencją zależności sztywność/grubość cienkich blach podczas zginania. Przy wyższych częstotliwościach, gdzie długość fali nie jest już dużo większa niż grubość płyty, zależności te załamują się. Prędkość fazowa rośnie coraz wolniej i zbliża się do prędkości fali Rayleigha w górnej granicy częstotliwości. Prędkość grupowa przechodzi przez maksimum, nieco szybciej niż prędkość fali poprzecznej, gdy długość fali jest w przybliżeniu równa grubości płyty. Następnie zbiega się z góry do prędkości fali Rayleigha w górnej granicy częstotliwości.

W eksperymentach, które umożliwiają wzbudzanie i wykrywanie zarówno modów rozciągających, jak i zginających, tryb rozciągający często pojawia się jako prekursor trybu zginania o większej prędkości i niższej amplitudzie. Tryb zginania jest łatwiejszy do wzbudzenia z tych dwóch i często przenosi większość energii.

Tryby wyższego rzędu

Wraz ze wzrostem częstotliwości pojawiają się tryby fal wyższego rzędu oprócz trybów zerowego rzędu. Każdy mod wyższego rzędu „rodzi się” przy częstotliwości rezonansowej płyty i istnieje tylko powyżej tej częstotliwości. Na przykład w 3 ⁄ 4 cala (19 mm) przy częstotliwości 200 kHz obecne są pierwsze cztery tryby fali Lamb, a przy 300 kHz pierwsze sześć. Kilka pierwszych modów wyższego rzędu można wyraźnie zaobserwować w sprzyjających warunkach eksperymentalnych. W mniej niż sprzyjających warunkach nakładają się na siebie i nie można ich rozróżnić.

Tryby Lamb wyższego rzędu charakteryzują się płaszczyznami węzłowymi w płycie, równoległymi do powierzchni płyty. Każdy z tych modów istnieje tylko powyżej pewnej częstotliwości, którą można nazwać jego "częstotliwością rodzącą się". Nie ma górnej granicy częstotliwości dla żadnego z trybów. Powstające częstotliwości można zobrazować jako częstotliwości rezonansowe dla fal podłużnych lub poprzecznych rozchodzących się prostopadle do płaszczyzny płyty, tj.

{\ Displaystyle d = {\ Frac {n \ lambda} {2}} \ quad \ quad {\ tekst {lub}} \ quad \ quad f = {\ Frac { nc}{2d}}}

gdzie n jest dowolną dodatnią liczbą całkowitą. Tutaj c może być albo prędkością fali podłużnej, albo prędkością fali ścinającej, a dla każdego wynikowego zestawu rezonansów odpowiednie tryby fali Lamba są na przemian symetryczne i antysymetryczne. Wzajemne oddziaływanie tych dwóch zestawów daje w efekcie wzór rodzących się częstotliwości, który na pierwszy rzut oka wydaje się nieregularny. Na przykład w stalowej płycie o grubości 3/4 cala (19 mm) mającej prędkości wzdłużne i ścinające odpowiednio 5890 m/s i 3260 m/s, powstające częstotliwości modów antysymetrycznych A 1 _i A ₂ wynoszą odpowiednio 86 kHz i 310 kHz, podczas gdy powstające częstotliwości modów symetrycznych S1 _, S2 _i S3 _wynoszą odpowiednio 155 kHz, 172 kHz i 343 kHz.

Przy powstającej częstotliwości każdy z tych modów ma nieskończoną prędkość fazową i prędkość grupową równą zero. W górnej granicy częstotliwości prędkości fazowe i grupowe wszystkich tych modów zbiegają się z prędkością fali poprzecznej. Ze względu na te zbieżności prędkości Rayleigha i prędkości ścinania (które są bardzo blisko siebie) mają duże znaczenie w grubych płytach. Mówiąc najprościej, jeśli chodzi o materiał o największym znaczeniu inżynieryjnym, większość energii fal o wysokiej częstotliwości, która rozchodzi się na duże odległości w płytach stalowych, przemieszcza się z prędkością 3000–3300 m/s.

Ruch cząstek w trybach fali Lamba jest na ogół eliptyczny i ma składowe zarówno prostopadłe, jak i równoległe do płaszczyzny płytki. Te składowe są kwadraturowe, tzn. mają różnicę faz 90°. Względna wielkość składowych jest funkcją częstotliwości. W przypadku pewnych iloczynów częstotliwości i grubości amplituda jednej składowej przechodzi przez zero, tak że ruch jest całkowicie prostopadły lub równoległy do płaszczyzny płyty. Dla cząstek na powierzchni płyty warunki te występują, gdy prędkość fazowa fali Lamba wynosi √ 2 c _t lub tylko dla modów symetrycznych c _l odpowiednio. Te rozważania dotyczące kierunkowości są ważne przy rozważaniu promieniowania energii akustycznej z płyt do sąsiednich płynów.

Ruch cząstek jest również całkowicie prostopadły lub całkowicie równoległy do płaszczyzny płyty, przy powstającej częstotliwości modu. W pobliżu powstających częstotliwości modów odpowiadających rezonansom podłużnym płyty, ich ruch cząstek będzie prawie całkowicie prostopadły do płaszczyzny płyty; iw pobliżu rezonansów fali ścinającej, równolegle.

J. i H. Krautkrämer wskazali, że fale Lamba można sobie wyobrazić jako układ fal podłużnych i poprzecznych rozchodzących się pod odpowiednimi kątami w poprzek i wzdłuż płyty. Fale te odbijają się i przekształcają w tryby, a następnie łączą się, tworząc trwały, spójny wzór fal. Aby powstał spójny wzór fal, grubość płyty musi być dokładnie dopasowana do kątów propagacji i długości fal leżących pod spodem fal podłużnych i poprzecznych; wymaganie to prowadzi do zależności dyspersji prędkości.

Fale jagnięce o cylindrycznej symetrii; fale płytowe ze źródeł punktowych

Podczas gdy analiza Lamba zakładała proste czoło fali, wykazano, że te same równania charakterystyczne odnoszą się do fal cylindrycznych (tj. fal rozchodzących się na zewnątrz od źródła liniowego, którego linia leży prostopadle do płyty). Różnica polega na tym, że podczas gdy „nośną” dla prostego czoła fali jest sinusoida, „nośną” dla fali osiowosymetrycznej jest funkcja Bessela. Funkcja Bessela dba o osobliwość u źródła, a następnie zbiega się w kierunku zachowania sinusoidalnego na dużych odległościach.

Te cylindryczne fale są funkcjami własnymi, z których można skomponować odpowiedź płyty na zakłócenia punktowe. Zatem odpowiedź płytki na zakłócenie punktowe można wyrazić jako kombinację fal Lamba oraz zanikających składników w polu bliskim. Ogólny wynik można luźno zobrazować jako wzór okrągłych frontów falowych, takich jak zmarszczki po kamieniu wrzuconym do stawu, ale zmieniające się głębiej w miarę przemieszczania się na zewnątrz. Teoria fal jagnięcych odnosi się tylko do ruchu w kierunku (r, z); ruch poprzeczny to inny temat.

Prowadzone fale jagnięce

To sformułowanie jest dość często spotykane w badaniach nieniszczących. „Guided Lamb Waves” można zdefiniować jako fale podobne do Lamb, które są kierowane przez skończone wymiary rzeczywistych obiektów testowych. Dodanie przedrostka „kierowany” do wyrażenia „fala Baranka” oznacza zatem uznanie, że nieskończonej płyty Baranka w rzeczywistości nigdzie nie można znaleźć.

W rzeczywistości mamy do czynienia z skończonymi płytami lub płytami owiniętymi w cylindryczne rury lub naczynia, lub płytami pociętymi na cienkie paski itp. Teoria fal Lamb często bardzo dobrze opisuje zachowanie falowe takich struktur. Nie da to idealnego opisu i dlatego wyrażenie „Guided Lamb Waves” jest bardziej praktyczne niż „Lamb Waves”. Jedno pytanie dotyczy tego, w jaki sposób rzeczywista geometria części wpłynie na prędkości i kształty modów fal podobnych do Baranka. Na przykład prędkość fali podobnej do Baranka w cienkim cylindrze będzie nieco zależeć od promienia cylindra i od tego, czy fala porusza się wzdłuż osi, czy wokół obwodu. Innym pytaniem jest, jakie zupełnie inne zachowania akustyczne i tryby fal mogą występować w rzeczywistej geometrii części. Na przykład rura cylindryczna ma tryby zginania związane z ruchem ciała całej rury, zupełnie różne od trybu zginania ścianki rury podobnego do Baranka.

Fale jagnięce w badaniach ultradźwiękowych

Celem badań ultradźwiękowych jest zwykle znalezienie i scharakteryzowanie poszczególnych wad badanego obiektu. Takie wady są wykrywane, gdy odbijają lub rozpraszają uderzającą falę, a odbita lub rozproszona fala dociera do jednostki poszukiwawczej z wystarczającą amplitudą.

Tradycyjnie badania ultradźwiękowe były przeprowadzane za pomocą fal, których długość fali jest znacznie krótsza niż wymiar kontrolowanej części. W tym reżimie wysokich częstotliwości inspektor ultradźwiękowy wykorzystuje fale zbliżone do trybów fali podłużnej i ścinającej o nieskończoności średniej, zygzakowate do iz całej grubości płyty. Chociaż pionierzy fal jagnięcych pracowali nad nieniszczącymi aplikacjami do testowania i zwrócili uwagę na teorię, powszechne zastosowanie pojawiło się dopiero w latach 90. XX wieku, kiedy programy komputerowe do obliczania krzywych dyspersji i odnoszenia ich do sygnałów obserwowalnych eksperymentalnie stały się znacznie szerzej dostępne. Te narzędzia obliczeniowe, wraz z szerszym zrozumieniem natury fal Lamba, umożliwiły opracowanie technik badań nieniszczących przy użyciu długości fal, które są porównywalne lub większe od grubości płytki. Przy tych dłuższych długościach fal tłumienie fali jest mniejsze, dzięki czemu można wykrywać wady z większej odległości.

Głównym wyzwaniem i umiejętnością wykorzystania fal Lamb do badań ultradźwiękowych jest generowanie określonych modów przy określonych częstotliwościach, które będą się dobrze propagować i dawać czyste „echo” powrotne. Wymaga to starannej kontroli wzbudzenia. Techniki do tego celu obejmują zastosowanie przetworników grzebieniowych, klinów, fal z płynnych mediów i elektromagnetycznych przetworników akustycznych ( EMAT ).

Fale jagnięce w badaniach akustyczno-ultradźwiękowych

Testy akustyczno-ultradźwiękowe różnią się od testów ultradźwiękowych tym, że zostały pomyślane jako sposób oceny uszkodzeń (i innych właściwości materiału) rozłożonych na znacznych obszarach, zamiast charakteryzowania wad indywidualnie. Fale jagnięce dobrze pasują do tej koncepcji, ponieważ napromieniowują całą grubość płyty i rozchodzą się na znaczne odległości ze spójnymi wzorcami ruchu.

Fale jagnięce w badaniach emisji akustycznej

Emisja akustyczna wykorzystuje znacznie niższe częstotliwości niż tradycyjne testy ultradźwiękowe, a zwykle oczekuje się, że czujnik wykryje aktywne defekty z odległości do kilku metrów. Duża część konstrukcji zwykle testowanych z emisją akustyczną jest wytwarzana z blachy stalowej - zbiorniki, zbiorniki ciśnieniowe, rury i tak dalej. Teoria fal jagnięcych jest zatem podstawową teorią wyjaśniającą formy sygnału i prędkości propagacji obserwowane podczas przeprowadzania testów emisji akustycznej. Znaczącą poprawę dokładności lokalizacji źródła AE (główna technika testowania AE) można osiągnąć dzięki dobremu zrozumieniu i umiejętnemu wykorzystaniu wiedzy o falach Lamba.

Porównanie badań emisji ultradźwiękowej i akustycznej

Dowolne mechaniczne wzbudzenie przyłożone do płytki wygeneruje wiele fal Lamb przenoszących energię w całym zakresie częstotliwości. Tak jest w przypadku fali emisji akustycznej. W testach emisji akustycznej wyzwaniem jest rozpoznanie wielu składowych fali Lamba w odebranym kształcie fali i zinterpretowanie ich w kategoriach ruchu źródła. Kontrastuje to z sytuacją w testach ultradźwiękowych, gdzie pierwszym wyzwaniem jest wygenerowanie pojedynczego, dobrze kontrolowanego trybu fali Lamb na jednej częstotliwości. Ale nawet w testach ultradźwiękowych konwersja modów ma miejsce, gdy generowana fala Lamb oddziałuje z wadami, więc interpretacja odbitych sygnałów złożonych z wielu modów staje się sposobem na scharakteryzowanie wad.

Zobacz też

^ Baranek, Horacy (1881). „O wibracjach elastycznej kuli” . Proceedings of London Mathematical Society . s1-13 (1): 189-212. doi : 10.1112/plms/s1-13.1.189 . ISSN 1460-244X .
^ Achenbach, JD „Rozprzestrzenianie się fal w elastycznych ciałach stałych”. Nowy Jork: Elsevier, 1984.
^ Lamb, H. „O falach w elastycznej płycie”. proc. Roya. soc. Londyn, ser. A 93, 114-128, 1917.
^ Viktorov, IA „Rayleigh i Lamb Waves: teoria fizyczna i zastosowania”, Plenum Press, Nowy Jork, 1967.
^ Huber, A. „Kalkulator dyspersji” . Strona główna DLR . Niemieckie Centrum Lotnictwa i Kosmonautyki (DLR) . Źródło 13 marca 2021 r .
^ Ten link pokazuje wideo ruchu cząstek.
^ J. i H. Krautkrämer, „Ultrasonic Testing of Materials”, wydanie 4, American Society for Testing and Materials, ISBN 0-318-21482-2 , kwiecień 1990.
^ Claes, S., "La forme des signaux d'émission acoustique et leur rola dans les essais de localisation", Journées d'Etudes sur l'Emission Acoustique, Institut National des Sciences Appliquées, Lyon (Francja), 17-18 marca , P. 215-257, 1975.

Róża, JL; „Fale ultradźwiękowe w ośrodkach stałych”, Cambridge University Press, 1999.

Linki zewnętrzne

Tryby propagacji fali dźwiękowej w Centrum Zasobów NDT
Fala Baranka w Encyklopedii Badań Nieniszczących
Analiza Lamb Wave of Acousto-Ultrasonic Signals in Plate autorstwa Liu Zhenqing: artykuł, który zawiera pełne równania fal Lamb.

[1] Baranek, Horacy (1881). „O wibracjach elastycznej kuli” . Proceedings of London Mathematical Society . s1-13 (1): 189-212. doi : 10.1112/plms/s1-13.1.189 . ISSN 1460-244X .

[2] Achenbach, JD „Rozprzestrzenianie się fal w elastycznych ciałach stałych”. Nowy Jork: Elsevier, 1984.

[3] Lamb, H. „O falach w elastycznej płycie”. proc. Roya. soc. Londyn, ser. A 93, 114-128, 1917.

[4] Viktorov, IA „Rayleigh i Lamb Waves: teoria fizyczna i zastosowania”, Plenum Press, Nowy Jork, 1967.

[5] Huber, A. „Kalkulator dyspersji” . Strona główna DLR . Niemieckie Centrum Lotnictwa i Kosmonautyki (DLR) . Źródło 13 marca 2021 r .

[6] Ten link pokazuje wideo ruchu cząstek.

[7] J. i H. Krautkrämer, „Ultrasonic Testing of Materials”, wydanie 4, American Society for Testing and Materials, ISBN 0-318-21482-2 , kwiecień 1990.

[8] Claes, S., "La forme des signaux d'émission acoustique et leur rola dans les essais de localisation", Journées d'Etudes sur l'Emission Acoustique, Institut National des Sciences Appliquées, Lyon (Francja), 17-18 marca , P. 215-257, 1975.