Filtr (symulacja dużych wirów)

Filtrowanie w kontekście symulacji dużych wirów (LES) to operacja matematyczna mająca na celu usunięcie zakresu małych skal z rozwiązania równań Naviera-Stokesa . Ponieważ główna trudność w symulowaniu przepływów turbulentnych wynika z szerokiego zakresu skal długości i czasu, ta operacja sprawia, że ​​symulacja przepływu turbulentnego jest tańsza, ponieważ zmniejsza zakres skal, które należy rozwiązać. Działanie filtra LES jest dolnoprzepustowe, co oznacza, że ​​odfiltrowuje skale związane z wysokimi częstotliwościami.

Filtry jednorodne

Pole prędkości wytworzone przez bezpośrednią symulację numeryczną (DNS) jednorodnej zanikającej turbulencji . Rozmiar domeny to L ³ .

To samo pole prędkości DNS filtrowane przy użyciu filtra pudełkowego i Δ = L /32

To samo pole prędkości DNS filtrowane przy użyciu filtra pudełkowego i Δ = L /16

Definicja w przestrzeni fizycznej

$.$ dolnoprzepustowego używaną w LES można zastosować do pola przestrzennego , Działanie filtra LES może być przestrzenne, czasowe lub jedno i drugie. Filtrowane pole, oznaczone kreską, jest zdefiniowane jako:

${\ Displaystyle {\ overline {\ phi ( {\ boldsymbol {x}}, t)}} = \ Displaystyle {\ int _ {- \ infty} ^ {\ infty}} \ int _ {- \ infty} ^ {\ infty} \ phi ({\ boldsymbol { r}},t^{\prime})G({\boldsymbol {x}}-{\boldsymbol {r}},tt^{\prime})dt^{\prime}d{\boldsymbol {r}} ,}$

gdzie jest $splotu$ unikalnym dla używanego typu filtra. Można to zapisać jako operację splotu:

${\ Displaystyle {\ overline {\ fi}} = G \ gwiazda \ fi.}$

${$ filtra wykorzystuje długość odcięcia i skale czasowe, oznaczone odpowiednio i $c}}$$displaystyle \ tau _$ Skale mniejsze od tych są eliminowane z $phi}}.}$$\$ Korzystając z tej definicji, dowolne pole podzielić na część filtrowaną i podfiltrowaną (oznaczoną liczbą pierwszą), jak

${\ Displaystyle \ phi = {\ bar {\ phi}} + \ phi ^ {\ pierwsza}.}$

Można to również zapisać jako operację splotu,

${\ Displaystyle \ fi ^ {\ pierwsza} = \ lewo (1-G \ prawo) \ gwiazda \ fi.}$

Definicja w przestrzeni widmowej

Operacja filtrowania usuwa skale związane z wysokimi częstotliwościami, a operacja może być odpowiednio interpretowana w przestrzeni Fouriera . Dla pola skalarnego transformata Fouriera z wynosi ϕ $\ Displaystyle \ phi} ϕ ^ ( k , ω ) ϕ ( x , t ) ,$${$${$$\ Displaystyle {\ hat {\ phi}} ({\ boldsymbol {k}}, \ omega),}$ funkcja ${\ Displaystyle {\ boldsymbol {k}}}$ przestrzennej liczby fal i ${ \displaystyle \omega ,}$ częstotliwość czasowa. ${\ Displaystyle {\ hat {\ phi}}}$ może być filtrowane przez odpowiednią transformatę Fouriera jądra filtra, oznaczoną ${\ Displaystyle {\ hat {G}} ({\ boldsymbol {k}},\omega):}$

${\ Displaystyle {\ overline {\ kapelusz {\ fi}}} ({\ pogrubiony symbol {k}}, \ omega) = {\ kapelusz {\ fi}} ({\ pogrubiony symbol {k}}, \ omega) {\ kapelusz {G}} ({\ pogrubiony symbol {k}}, \ omega)}$

Lub,

${\ Displaystyle {\ overline {\ kapelusz {\ fi}}} = {\ kapelusz {G}} {\ kapelusz {\ fi}}.}$

$a$ filtra ma powiązany numer fali odcięcia $\$ szerokość filtra $Delta}$ również powiązany punkt odcięcia częstotliwość ${\ Displaystyle \ omega _ {c}.}$ Niefiltrowana część ${\ Displaystyle {\ hat {\ phi}}}$ to:

${\ Displaystyle {\ kapelusz {\ fi ^ {\ pierwsza}}} = (1- {\ kapelusz {G}}) {\ kapelusz {\ fi}}.}$

Widmowa interpretacja operacji filtrowania ma zasadnicze znaczenie dla operacji filtrowania w symulacji dużych wirów, ponieważ widma przepływów turbulentnych mają kluczowe znaczenie dla modeli w skali podsiatki LES, które rekonstruują wpływ skal podfiltra (najwyższe częstotliwości). Jednym z wyzwań w modelowaniu podsieci jest skuteczne naśladowanie kaskady energii kinetycznej od niskich do wysokich częstotliwości. To sprawia, że ​​właściwości widmowe zaimplementowanego filtra LES są bardzo ważne w modelowaniu podsieci.

Jednorodne właściwości filtra

Homogeniczne filtry LES muszą spełniać następujący zestaw właściwości po zastosowaniu do równań Naviera-Stokesa.

$oznacza$

Zachowanie stałych Wartość filtrowanej

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} G ({\ boldsymbol {\ xi }},t^{\prime })d^{3}{\boldsymbol {\xi }}dt^{\prime }=1.} 2.$

być równa stałej,

,

Liniowość

${\ Displaystyle {\ overline {\ phi + \ psi}} = {\ overline {\ phi}} + {\ overline {\ psi}}.} 3. Komutacja z$

pochodnymi

$}$

${\ Displaystyle {\ overline {\ Frac {\ częściowe \ phi} {\ częściowe s}}} = {\ frac {\ częściowe {\ overline {\ phi}}} {\ częściowe s}}, \ qquad s = { \boldsymbol {x}}, t$

Jeśli wprowadzono notację dla komutacji operatora $\$ dwóch dowolnych operatorów i ${\ displaystyle g$ } $sol$ sol

${\ Displaystyle [f, g] \ phi = f \ circ g(\phi )-g\circ f(\phi )=f(g(\phi ))-g(f(\phi )),} wtedy ta$

trzecia własność może być wyrażona jako

${\ Displaystyle \ lewo [G \ gwiazda, {\ Frac {\ częściowe} {\ częściowe s}} \ prawej] = 0.}$

Filtry spełniające te właściwości generalnie nie są operatorami Reynoldsa , co oznacza po pierwsze:

${\ Displaystyle {\ rozpocząć {tablica}} {rcl} {\ overline {\ overline {\ phi}}} & \ neq & {\overline {\phi}},\\G\star G\star \phi =G^{2}\star \phi &\neq &G\star \phi,\end{tablica}}}$

i drugi,

${\ Displaystyle {\ overline {\ phi ^ {\ pierwsza}}} = G \ gwiazda (1-G) \ gwiazda \ phi \ neq 0.}$

Filtry niejednorodne

Implementacje operacji filtrowania dla wszystkich przepływów oprócz najprostszych są niejednorodnymi operacjami filtrowania. Oznacza to, że przepływ albo $co$ powoduje problemy z niektórymi typami filtrów, albo ma niestałą szerokość filtra , albo jedno i drugie. Zapobiega to komutacji filtra z pochodnymi, a operacja komutacji prowadzi do kilku dodatkowych błędów:

${ \ Displaystyle {\ rozpocząć {tablica} {rcl} \ lewo [{\ Frac {\ częściowe}} {\ częściowe {\ pogrubiony symbol {x}}}}, G \ gwiazda \ po prawej] \ phi & = & {\ frac {\ częściowy }{\częściowy {\boldsymbol {x}}}}\left(G\star \phi \right)-G\star {\frac {\częściowy \phi}}{\częściowy {\boldsymbol {x}}}} \\&=&{\frac {\częściowy}}{\częściowy {\boldsymbol {x}}}}\int _{\Omega}G({\boldsymbol {x}}-{\boldsymbol {r}},\ Delta ({\boldsymbol {x}},t))\phi ({\boldsymbol {r}},t)d{\boldsymbol {r}}-G\star {\frac {\częściowy \phi}}{\częściowy {\boldsymbol {x}}}}\\&=&\left({\frac {\częściowe G}{\częściowe \Delta}}\star \phi \right){\frac {\częściowe \Delta}}{\ częściowe x}}+\int _{d\Omega }G(xr,\Delta (x,t))\phi (r,t){\boldsymbol {n}}dS\end{tablica}},}$

gdzie $jest wektorem$${\ Displaystyle d \ Omega.}$ powierzchni $re$ Ω

Oba terminy pojawiają się z powodu niejednorodności. Pierwsza wynika z przestrzennej zmienności rozmiaru filtra $druga$ z powodu granicy domeny. Podobnie komutacja filtra z pochodną czasową prowadzi do składnika błędu wynikającego z czasowej zmiany rozmiaru filtra, ${\ displaystyle G}$

${\ Displaystyle \ lewo [{\ Frac {\ częściowe} {\ częściowe t}}, G \ gwiazda \ po prawej] = \ lewo ({\ Frac {\ częściowe G} {\ częściowe \ Delta}} \ gwiazda \ phi \ dobrze) {\ frac {\ częściowe \ Delta } {\ częściowe t}}.}$

Zaproponowano kilka operacji filtrowania, które eliminują lub minimalizują te składniki błędów.

Klasyczne filtry symulacji dużych wirów

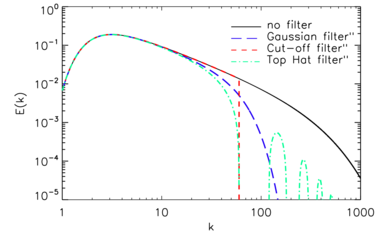
Widmo energii turbulentnej i efekty operacji filtracyjnych

Istnieją trzy filtry zwykle używane do filtrowania przestrzennego w symulacji dużych wirów. Definicja ${\ Displaystyle G ({\ boldsymbol {x}}, t)}$ i ${\ Displaystyle {\ kapelusz {G}} ({\ boldsymbol {k }},\omega )}$ i omówienie ważnych właściwości.

Filtr pudełkowy

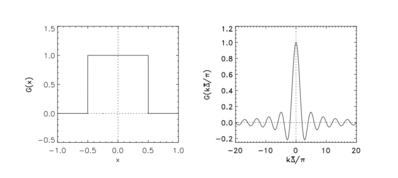
Filtr pudełkowy w przestrzeni fizycznej i widmowej

Jądro filtra w przestrzeni fizycznej jest określone przez:

${\ Displaystyle G ({\ boldsymbol {x}} - {\ boldsymbol {r}}) = {\ rozpocząć {przypadki} {\ Frac {1} {\ Delta}}, & {\ tekst {jeśli}} \ lewo |{\boldsymbol {x}}-{\boldsymbol {r}}\right|\leq {\frac {\Delta }{2}},\\0,&{\text{inaczej}}.\end{cases }}}$

Jądro filtra w przestrzeni widmowej jest określone przez:

${\ Displaystyle {\ kapelusz {G}} ({\ boldsymbol {k}}) = {\ Frac {\ sin {({\ Frac {1} {2}} k \ Delta)}} {{\ Frac {1 }{2}}k\Delta }}.}$

Filtr Gaussa w przestrzeni fizycznej i widmowej

Filtr Gaussa

Jądro filtra w przestrzeni fizycznej jest określone przez:

${\ Displaystyle G ({\ boldsymbol {x}} - {\ boldsymbol {r}}) = \ lewo ({\ Frac {6} {\ pi \ Delta ^ {2}}} \ prawej) ^ {\ frac { 1}{2}}\exp {\left(-{\frac {6({\boldsymbol {xr}})^{2}}{\Delta ^{2}}}\right)}.}$

Jądro filtra w przestrzeni widmowej jest określone przez:

${\ Displaystyle {\ kapelusz {G}} ({\ boldsymbol {k}}) = \ exp {\ lewo (- {\ Frac {{\ boldsymbol {k}} ^ {2} \ Delta ^ {2}} 24}}\prawo)}.}$

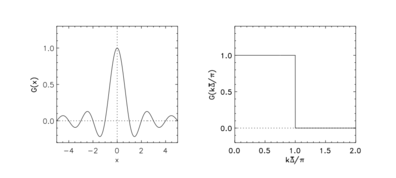
Ostry filtr widmowy w przestrzeni fizycznej i widmowej

Ostry filtr widmowy

Jądro filtra w przestrzeni fizycznej jest określone przez:

${\ Displaystyle G ({\ boldsymbol {x}} - {\ boldsymbol {r}}) = {\ Frac {\ sin {(\ pi ({\ boldsymbol {xr}}) / \ Delta)}} {\ pi ({\boldsymbol {xr}})}}.}$

Jądro filtra w przestrzeni widmowej jest określone przez:

${\ Displaystyle {\ kapelusz {G}} ({\ boldsymbol {k}}) = H \ lewo (k_ {c} - \ lewo | k \ prawo | \ prawo), \ qquad k_ {c} = {\ frac {\pi} {\Delta}}.}$

Zobacz też

• Obliczeniowa dynamika płynów
• Filtr (przetwarzanie sygnału)
• Mechanika płynów
• Transformata Fouriera
• Domena częstotliwości
• Symulacja dużych wirów
• Turbulencja