Funkcja totient Eulera

„φ (n)” przekierowuje tutaj. W przypadku innych zastosowań zobacz Phi .

Nie mylić z funkcją Eulera .

Pierwszy tysiąc wartości φ ( n ) . Punkty na górnym wierszu reprezentują φ ( p ), gdy p jest liczbą pierwszą, czyli p − 1.

W teorii liczb funkcja totient Eulera zlicza dodatnie liczby całkowite do danej liczby całkowitej n , które są względnie pierwsze od n . Jest napisany $użyciu$ litery $phi$ jako lub i również Eulera Innymi słowy, jest to liczba liczb całkowitych k z zakresu 1 ≤ k ≤ n , dla których największy wspólny dzielnik gcd( n , k ) jest równy 1. Liczby całkowite k tej postaci są czasami określane jako sumy n .

Na przykład sumy n = 9 to sześć liczb 1, 2, 4, 5, 7 i 8. Wszystkie są względnie pierwsze do 9, ale pozostałe trzy liczby z tego zakresu, 3, 6 i 9, nie są , ponieważ wcd(9, 3) = wcd(9, 6) = 3 i wcd(9, 9) = 9 . Dlatego φ (9) = 6 . Jako inny przykład, φ (1) = 1 , ponieważ dla n = 1 jedyną liczbą całkowitą w zakresie od 1 do n jest sama 1, a gcd(1, 1) = 1 .

Funkcja totient Eulera jest funkcją multiplikatywną , co oznacza, że ​​jeśli dwie liczby m i n są względnie pierwsze, to φ ( mn ) = φ ( m ) φ ( n ) . $_$ funkcja podaje rząd multiplikatywnej grupy n liczb całkowitych ( grupa jednostek pierścienia Służy również do definiowania systemu szyfrowania RSA .

Historia, terminologia i notacja

Leonhard Euler wprowadził tę funkcję w 1763 r. Nie wybrał jednak wówczas żadnego konkretnego symbolu, który by ją oznaczał. W publikacji z 1784 roku Euler zbadał tę funkcję dalej, wybierając grecką literę π do jej oznaczenia: napisał πD dla „mnóstwa liczb mniejszych niż D i które nie mają z nią wspólnego dzielnika”. Ta definicja różni się od obecnej definicji funkcji totient przy D = 1 , ale poza tym jest taka sama. Obecnie standardowa notacja φ ( A ) pochodzi z traktatu Gaussa z 1801 r. Disquisitiones Arithmeticae , chociaż Gauss nie użył nawiasów wokół argumentu i napisał φA . Dlatego jest często nazywana funkcją phi Eulera lub po prostu funkcją phi .

W 1879 roku JJ Sylvester ukuł termin totient dla tej funkcji, dlatego jest on również określany jako funkcja totient Eulera , totient Eulera lub totient Eulera . Totient Jordana jest uogólnieniem Eulera.

Współczynnik n n - φ ( n jest zdefiniowany jako ) . Zlicza liczbę dodatnich liczb całkowitych mniejszych lub równych n , które mają co najmniej jeden wspólny czynnik pierwszy z n .

Obliczanie funkcji totient Eulera

Istnieje kilka wzorów obliczania φ ( n ) .

Formuła produktu Eulera

W Stanach

${\ Displaystyle \ varphi (n) = n \ prod _ {p \ środkowy n} \ lewo (1 - {\ Frac {1} {p} }\Prawidłowy),}$

gdzie iloczyn jest nad różnymi liczbami pierwszymi dzielącymi n . (Aby zapoznać się z notacją, zobacz Funkcja arytmetyczna ).

Równoważne sformułowanie dla ${\ Displaystyle n = p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} \ cdots p_ { r} ^ {k_ {r}}}$ , gdzie ${\ Displaystyle p_ {1}, p_ {2}, \ ldots, p_ {r}}$ to różne liczby pierwsze dzielące n , Jest:

$${\ Displaystyle \ varphi (n) = p_ {1} ^ {k_ {1} -1} (p_ {1} {-} 1) \, p_ {2} ^ {k_ {2} -1} (p_ { 2}{-}1)\cdots p_{r}^{k_{r}-1}(p_{r}{-}1).}$$

Dowód tych wzorów zależy od dwóch ważnych faktów.

Phi jest funkcją multiplikatywną

Oznacza to, że jeśli gcd( m , n ) = 1 , to φ ( m ) φ ( n ) = φ ( mn ) . Zarys dowodu: Niech A , B , C będą zbiorami dodatnich liczb całkowitych, które są odpowiednio pierwsze i mniejsze od m , n , mn , tak że | | _ = φ ( m ) itd. Wtedy istnieje bijekcja między A × B i C według chińskiego twierdzenia o resztach .

Wartość phi dla argumentu potęgi pierwszej

Jeśli p jest liczbą pierwszą i k ≥ 1 , to

${\ Displaystyle \ varphi \ lewo (p ^ {k} \ prawej) = p ^ {k} - p ^ {k-1} = p ^ {k-1} (p-1) = p ^ {k} \ lewo(1-{\tfrac {1}{p}}\prawo).}$

Dowód : Ponieważ p jest liczbą pierwszą, jedynymi możliwymi wartościami gcd( p ^k , m ) są 1, p , p ² , ..., p ^k i jedynym sposobem, aby gcd( p ^k , m ) > 1 jest wtedy, gdy m jest wielokrotnością p , to znaczy m ∈ { p , 2 p , 3 p , ..., p ^{k − 1} p = p ^k } , a są p ^{k − 1} takie wielokrotności nie większe niż pk ^_ . Dlatego wszystkie inne liczby p ^k − p ^{k − 1} są względnie pierwsze względem p ^k .

Dowód formuły produktu Eulera

Podstawowe twierdzenie arytmetyki mówi, że jeśli n > 1 istnieje unikalne wyrażenie ${\ Displaystyle n = p_ {1} ^ {k_ {1}} p_ { 2}^{k_{2}}\cdots p_{r}^{k_{r}},}$ gdzie p ₁ < p ₂ < ... < p _r są liczbami pierwszymi i każdy k _i ≥ 1 . (Przypadek n = 1 odpowiada pustemu iloczynowi.) Wielokrotne użycie multiplikatywnej właściwości φ i wzoru na φ ( p ^k ) daje

${\ Displaystyle {\ rozpocząć {tablica} {rcl} \ varphi (n) & = & \ varphi (p_ {1} ^ {k_ {1}}) \ \ varphi (p_ {2} ^ {k_ {2} })\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}-1}(p_{1}-1)\, p_{2}^{k_{2}-1}(p_{2}-1)\cdots p_{r}^{k_{r}-1}(p_{r}-1)\\[.1em] &=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1- {\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right) \\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\ frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_ {r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{ p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}}$

Daje to obie wersje formuły produktu Eulera.

$.$ nie wymaga właściwości multiplikatywnej, zamiast tego wykorzystuje do z zbiorów liczb całkowitych podzielnych przez pierwsze dzielniki.

Przykład

${\ Displaystyle \ varphi (20) = \ varphi (2 ^ {2}5)=20\,(1-{\tfrac {1}{2}})\,(1-{\tfrac {1}{5}})=20\cdot {\tfrac {1}{ 2}}\cdot {\tfrac {4}{5}}=8.}$

Innymi słowy: różne czynniki pierwsze liczby 20 to 2 i 5; połowa z dwudziestu liczb całkowitych od 1 do 20 jest podzielna przez 2, pozostawiając dziesięć; jedna piąta z nich jest podzielna przez 5, pozostawiając osiem liczb względnie pierwszych do 20; są to: 1, 3, 7, 9, 11, 13, 17, 19.

Alternatywna formuła używa tylko liczb całkowitych:

$${\ Displaystyle \ varphi (20) =\varphi (2^{2}5^{1})=2^{2-1}(2{-}1)\,5^{1-1}(5{-}1)=2\cdot 1\ckropka 1\ckropka 4=8.}$$

Transformata Fouriera

Totient jest dyskretną transformatą Fouriera gcd , ocenianą na 1. Niech

${\ Displaystyle {\ mathcal {F}} \ {\ mathbf {x} \} [m] = \ suma \ granice _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}}}$

gdzie x _k = gcd( k , n ) dla k ∈ {1, ..., n } . Następnie

${\ Displaystyle \ varphi (n) = {\ mathcal {F}} \ {\ mathbf {x} \} [1] = \ suma \ limity _ {k = 1} ^ {n} \ gcd (k, n) e^{-2\pi i {\frac {k}{n}}}.}$

Prawdziwa część tej formuły to

${\ Displaystyle \ varphi (n) = \ suma \ limity _ {k = 1} ^ {n} \ gcd (k, n) \ cos {\ tfrac {2 \ pi k} {n}}.}$

Na przykład za pomocą i ${\ Displaystyle \ cos {\ tfrac {\ pi}}$ } ${\ Displaystyle \ sałata {\ tfrac {2 \ pi}} {5}} = {\ tfrac {{\ sqrt {5}} -1} {4}}}$ :

$${\ Displaystyle { \begin{array}{rcl}\varphi (10)&=&\gcd(1,10)\cos {\tfrac {2\pi}}{10}}+\gcd(2,10)\cos {\tfrac {4\pi }{10}}+\gcd(3,10)\cos {\tfrac {6\pi }{10}}+\cdots +\gcd(10,10)\cos {\tfrac {20\ pi }{10}}\\&=&1\cdot ({\tfrac {{\sqrt {5}}+1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}- 1}{4}})+1\cdot (-{\tfrac {{\sqrt {5}}-1}{4}})+2\cdot (-{\tfrac {{\sqrt {5}}+ 1}{4}})+5\cdot (-1)\\&&+\ 2\cdot (-{\tfrac {{\sqrt {5}}+1}{4}})+1\cdot (- {\tfrac {{\sqrt {5}}-1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}-1}{4}})+1\cdot ({\ tfrac {{\sqrt {5}}+1}{4}})+10\cdot (1)\\&=&4.\end{tablica}}}$$

W przeciwieństwie do iloczynu Eulera i wzoru na sumę dzielników, ten nie wymaga znajomości czynników n . Wymaga to jednak obliczenia największego wspólnego dzielnika n i każdej dodatniej liczby całkowitej mniejszej niż n , co i tak wystarcza do rozłożenia na czynniki.

Suma dzielnika

Właściwość ustalona przez Gaussa, tj

${\ Displaystyle \ suma _ {d \ mid n} \ varphi (d) = n,}$

gdzie suma jest po wszystkich dodatnich dzielnikach d od n , można udowodnić na kilka sposobów. (Zobacz Funkcja arytmetyczna , aby zapoznać się z konwencjami notacji).

Jednym z dowodów jest zauważenie, że φ ( d ) jest również równe liczbie możliwych generatorów grupy cyklicznej C _d ; konkretnie, jeśli C _d = ⟨ g ⟩ z g ^d = 1 , to g ^k jest generatorem dla każdego k liczb względnie pierwszych do d . Ponieważ każdy element C _n generuje cykliczną podgrupę , a wszystkie podgrupy C _d ⊆ C _n są generowane przez dokładnie φ ( d ) elementy C _n , wzór jest następujący. Równoważnie, wzór można wyprowadzić za pomocą tego samego argumentu, który zastosowano do multiplikatywnej grupy n -tych pierwiastków jedności i pierwiastków pierwotnych d- tych jedności .

Formułę można również wyprowadzić z elementarnej arytmetyki. Na przykład niech n = 20 i rozważ dodatnie ułamki do 1 z mianownikiem 20:

${\ Displaystyle {\ tfrac {1} {20}}, \, {\ tfrac {2} {20}}, \, {\ tfrac {3} {20}}, \, {\ tfrac {4} {20} }},\,{\tfrac {5}{20}},\,{\tfrac {6}{20}},\,{\tfrac {7}{20}},\,{\tfrac {8} {20}},\,{\tfrac {9}{20}},\,{\tfrac {10}{20}},\,{\tfrac {11}{20}},\,{\tfrac { 12}{20}},\,{\tfrac {13}{20}},\,{\tfrac {14}{20}},\,{\tfrac {15}{20}},\,{\ tfrac {16}{20}},\,{\tfrac {17}{20}},\,{\tfrac {18}{20}},\,{\tfrac {19}{20}},\, {\tfrac {20}{20}}.}$

Umieść je w najniższych kategoriach:

${\ Displaystyle {\ tfrac {1} {20}}, \, {\ tfrac {1} {10}}, \, {\ tfrac {3} {20}}, \ ,{\tfrac {1}{5}},\,{\tfrac {1}{4}},\,{\tfrac {3}{10}},\,{\tfrac {7}{20}} ,\,{\tfrac {2}{5}},\,{\tfrac {9}{20}},\,{\tfrac {1}{2}},\,{\tfrac {11}{20 }},\,{\tfrac {3}{5}},\,{\tfrac {13}{20}},\,{\tfrac {7}{10}},\,{\tfrac {3} {4}},\,{\tfrac {4}{5}},\,{\tfrac {17}{20}},\,{\tfrac {9}{10}},\,{\tfrac { 19}{20}},\,{\tfrac {1}{1}}}$

Te dwadzieścia ułamków to wszystkie dodatnie k / d ≤ 1, których mianownikami są dzielniki d = 1, 2, 4, 5, 10, 20 . Ułamki z 20 jako mianownikiem , 7/20 to są pierwsze do te , , ; 9/20 względnie których 11/20 liczniki a 20 mianowicie 1/20 , 3/20 , , , 13/20 19/20 17/20 , , z definicji są to ułamki φ (20) . Podobnie istnieją φ (10) o mianowniku 10 i φ (5) o mianowniku 5 itd. Zatem zbiór dwudziestu ułamków jest dzielony na podzbiory o rozmiarze φ ( d ) dla każdego d dzielącego 20. Podobny argument dotyczy dowolnego n.

inwersja Möbiusa zastosowana do wzoru na sumę dzielników

${\ Displaystyle \ varphi (n) = \ suma _ {d \ mid n} \ mu \ lewo (d\right)\cdot {\frac {n}{d}}=n\sum _{d\mid n}{\frac {\mu (d)}{d}},}$

gdzie μ jest funkcją Möbiusa , funkcją multiplikatywną zdefiniowaną przez ${\ Displaystyle \ mu (p) = -1}$ i ${\ Displaystyle \ mu (p ^ {k}) =0}$ dla każdej liczby pierwszej p i k ≥ 2 . $przez$ wyprowadzić otrzymać ${\ textstyle \ suma _ {d \ mid n} {\ frac {\ mu (d)} {d}}.}$

Przykład:

$${\ Displaystyle {\ rozpocząć {wyrównane} \ varphi (20) i = \ mu (1) \ cdot 20 + \ mu (2 )\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\ cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{wyrównane}}}$$

Niektóre wartości

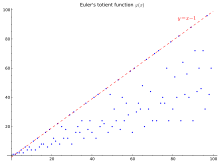
Pierwsze 100 wartości (sekwencja A000010 w OEIS ) przedstawiono w tabeli i na poniższym wykresie:

Wykres pierwszych 100 wartości

φ ( n ) dla 1 ≤ n ≤ 100

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

Na wykresie po prawej górna linia y = n - 1 jest górną granicą obowiązującą dla wszystkich n innych niż jeden i osiąganą wtedy i tylko wtedy, gdy n jest liczbą pierwszą. Prosta dolna granica to , $:$ jest raczej dolna do n / log log n .

Twierdzenie Eulera

Główny artykuł: twierdzenie Eulera

Stwierdza to, że jeśli a i n są względnie pierwsze, to

${\ Displaystyle a ^ {\ varphi (n)} \ równoważnik 1 \ mod n.}$

Szczególny przypadek, w którym n jest liczbą pierwszą, jest znany jako małe twierdzenie Fermata .

Wynika to z twierdzenia Lagrange'a oraz faktu, że φ ( n ) jest rzędem multiplikatywnej grupy liczb całkowitych modulo n .

Kryptosystem RSA opiera się na tym twierdzeniu: implikuje ono, że odwrotność b ↦ bd ^jest mod funkcji a ↦ ae mod n ^, gdzie n e jest (publicznym) wykładnikiem szyfrowania, funkcją , gdzie d , (prywatny ) wykładnik deszyfrowania, jest φ ( n multiplikatywną odwrotnością e modulo ) . Trudność obliczenia φ ( n ) bez znajomości faktoryzacji n jest zatem trudnością obliczenia d : jest to znane jako problem RSA , który można rozwiązać przez faktoring n . Właściciel klucza prywatnego zna rozkład na czynniki, ponieważ klucz prywatny RSA jest konstruowany poprzez wybranie n jako iloczynu dwóch (losowo wybranych) dużych liczb pierwszych p i q . Tylko n jest publicznie ujawniane, a biorąc pod uwagę trudność rozkładania dużych liczb na czynniki, mamy gwarancję, że nikt inny nie zna rozkładu na czynniki.

Inne formuły

• $\ Displaystyle a \ mid b \ implikuje \ varphi (a) \ mid \ varphi (b)}$
• ${\ Displaystyle m \ mid \ varphi (a ^ {m} -1)}$
• ${\ Displaystyle \ varphi (mn) = \ varphi (m) \ varphi (n) \ cdot {\frac {d}{\varphi (d)}}\quad {\text{gdzie}}d=\operatorname {gcd} (m,n)}$

  W szczególności:

  • ${\ Displaystyle \ varphi (2m) = {\ rozpocząć {przypadki} 2 \ varphi (m) i {\ tekst { if }}m{\text{ jest parzyste}}\\\varphi (m)&{\text{ if }}m{\text{ jest nieparzyste}}\end{przypadków}}}$
  • ${\ Displaystyle \ varphi \ lewo (n ^ {m} \ prawej) = n ^ {m-1} \ varphi (n)}$
• ${\ Displaystyle \ varphi (\ nazwa operatora {lcm} (m, n)} \ cdot \varphi (\operatorname {gcd} (m,n))=\varphi (m)\cdot \varphi (n)}$

  Porównaj to ze wzorem ${\ textstyle \ operatorname {lcm} (m, n) \ cdot \ operatorname {gcd} (m, n) = m\cdot n}$ (patrz najmniejsza wspólna wielokrotność ).

• φ ( n ) jest parzyste dla n ≥ 3 .

  Ponadto, jeśli n ma r różnych nieparzystych czynników pierwszych, 2 ^r | φ ( n )

• Dla dowolnych a > 1 i n > 6 takich, że 4 ∤ n istnieje l ≥ 2 n takie, że l | φ ( za ⁿ - 1) .
• ${\ Displaystyle {\ Frac {\ varphi (n)}} {n}} = {\ Frac {\ varphi (\ operatorname {rad} ( n))}{\nazwa_operatora {rad} (n)}}}$

  gdzie rad( n ) jest rodnikiem n (iloczynem wszystkich różnych liczb pierwszych dzielących n ).

• ${\ Displaystyle \ suma _ {d \ mid n} {\ Frac {\ mu ^ {2} (d)}} {\ varphi (d )}}={\frac {n}{\varphi (n)}}}$ 
• ${\ Displaystyle \ suma _ {1 \ równoważnik k \ równoważnik n \ na szczycie (k, n) = 1} \!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\text{dla }}n>1}$
• ${\ Displaystyle \ suma _ {k = 1} ^ {n} \ varphi (k) = {\ tfrac {1} {2}} \ lewo (1 + \ suma _ {k = 1 }^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi ^{2}} }n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}$ ( cytowany w)
• ${\ Displaystyle \ suma _ {k = 1} ^ {n} {\ Frac {\ varphi (k)}} {k}} = \ suma _ {k = 1} ^ {n} {\ Frac {\ mu (k )}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n )^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}$ 
• ${\ Displaystyle \ suma _ {k = 1} ^ {n }{\frac {k}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{ 2}}+O\left((\log n)^{\frac {2}{3}}\right)}$ 
• ${\ Displaystyle \ suma _ {k = 1} ^ {n} {\ Frac {1} {\ varphi (k)}} = {\ Frac {315 \, \ zeta (3)} {2 \ pi ^ { 4}}}\left(\log n+\gamma -\sum _{p{\text{prim}}}{\frac {\log p}{p^{2}-p+1}}\right)+ O\left({\frac {(\log n)^{\frac {2}{3}}}{n}}\right)}$ 

  (gdzie γ jest stałą Eulera – Mascheroniego ).

• ${\ Displaystyle \ suma _ {\ stackrel {1 \ równoważnik k \ równoważnik n} {\operatorname {gcd} (k,m)=1}}\!\!\!\!1=n{\frac {\varphi (m)}{m}}+O\left(2^{\omega (m)}\prawo)}$

  gdzie m > 1 jest dodatnią liczbą całkowitą, a ω ( m ) jest liczbą różnych czynników pierwszych m .

Tożsamość Menona

Główny artykuł: tożsamość Menona

W 1965 P. Keśawa Menon udowodnił

${\ Displaystyle \ suma _ {\ stackrel {1 \ równoważnik k \ równoważnik n} {\gcd(k,n)=1}}\!\!\!\!\gcd(k-1,n)=\varphi (n)d(n)}$

gdzie ₀ d ( n ) = σ ( n ) jest liczbą dzielników n .

Funkcje generujące

Szereg Dirichleta dla φ ( n ) można zapisać w kategoriach funkcji zeta Riemanna jako:

${\ Displaystyle \ suma _ {n = 1} ^ {\ infty} {\ Frac {\ varphi (n)}} {n ^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}}$

gdzie lewa strona zbiega się dla ${\ Displaystyle \ Re (s)> 2}$ .

Funkcja generująca szereg Lamberta to

${\ Displaystyle \ suma _ {n = 1} ^ {\ infty} {\ Frac {\ varphi (n) q ^ {n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}}$

który jest zbieżny dla | q | < 1 .

Oba są udowodnione przez elementarne manipulacje szeregami i wzory na φ ( n ) .

Tempo wzrostu

Mówiąc słowami Hardy'ego i Wrighta, kolejność φ ( n ) to „zawsze„ prawie n ”.

Pierwszy

${\ Displaystyle \ lim \ sup {\ Frac {\ varphi (n)} {n}} = 1,}$

ale gdy n dąży do nieskończoności, dla wszystkich δ > 0

${\ Displaystyle {\ Frac {\ varphi (n)} {n ^ {1-\ delta}}} \ rightarrow \ infty.}$

Te dwa wzory można udowodnić, używając niewiele więcej niż wzorów na φ ( n ) i funkcji sumy dzielników σ ( n ) .

W rzeczywistości podczas dowodu drugiej formuły nierówność

${\ Displaystyle {\ Frac {6} {\ pi ^ {2}}} < {\ Frac {\ varphi (n) \ sigma (n) }{n^{2}}}<1,}$

prawdziwe dla n > 1 , jest udowodnione.

Mamy też

${\ Displaystyle \ lim \ inf {\ Frac {\ varphi (n)}} {n}} \ log \ log n = e ^ {- \ gamma}.}$

Tutaj γ jest stałą Eulera γ e = 0,577215665... , ^{- γ} = 0,56145948... więc e ^γ = 1,7810724... i .

Udowodnienie tego nie wymaga twierdzenia o liczbach pierwszych . Ponieważ log log n dąży do nieskończoności, ta formuła to pokazuje

${\ Displaystyle \ lim \ inf {\ Frac {\ varphi (n)} {n}} = 0.}$

W rzeczywistości więcej jest prawdą.

${\ Displaystyle \ varphi (n)> {\ Frac {n} {e ^ {\ gamma} \; \ log \log n+{\frac {3}{\log \log n}}}}\quad {\text{dla }}n>2}$

I

${\ Displaystyle \ varphi (n) <{\ Frac {n} {e ^ {\ gamma} \ log \ log n}} \ quad {\ tekst {dla nieskończenie wielu}} n.}$

Drugą nierówność pokazał Jean-Louis Nicolas . Ribenboim mówi: „Metoda dowodu jest interesująca, ponieważ nierówność jest pokazana najpierw przy założeniu, że hipoteza Riemanna jest prawdziwa, a po drugie przy założeniu przeciwnym”.

Dla średniego zamówienia mamy

${\ styl wyświetlania \varphi (1)+\varphi (2)+\cdots +\varphi (n)={\frac {3n^{2}}{\pi ^{2}}}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)\quad {\text{as}}n\rightarrow \infty ,}$

dzięki Arnoldowi Walfiszowi , dowód wykorzystujący oszacowania na sumach wykładniczych należnych IM Vinogradovowi i NM Korobovowi . Dzięki połączeniu metod van der Corputa i Vinogradova, H.-Q. Liu (O funkcji Eulera. Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), nr 4, 769–775) poprawił składnik błędu do

${\ Displaystyle O \ lewo (n (\ log n) ^ {\ Frac {2} {3}} (\ log \ log n )^{\frac {1}{3}}\right)}$

(jest to obecnie najbardziej znane oszacowanie tego typu). „Duże ” oznacza O wielkość ograniczoną przez stałą pomnożoną przez funkcję n wewnątrz nawiasów (która jest mała w porównaniu z n ² ).

Wynik ten można wykorzystać do udowodnienia, że ​​prawdopodobieństwo, że dwie losowo wybrane liczby są względnie pierwsze, wynosi 6 / π ² .

Stosunek kolejnych wartości

W 1950 Somayajulu udowodnił

${\ Displaystyle {\ rozpocząć {wyrównane} \ lim \ inf {\ Frac {\ varphi (n + 1)} {\ varphi (n)}} & = 0 \ quad {\ tekst {i}} \\ [5px] \lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}&=\infty .\end{wyrównane}}}$

W 1954 roku Schinzel i Sierpiński wzmocnili to, udowadniając, że zestaw

${\ Displaystyle \ lewo \ {{\ Frac {\ varphi (n + 1)} {\ varphi (n)}} \; \;n=1,2,\ldkropki \po prawej\}}$

jest gęsty w dodatnich liczbach rzeczywistych. Udowodnili również, że zestaw

${\ Displaystyle \ lewo \ {{\ Frac {\ varphi (n)} {n}}, \; \; n = 1,2 \ ldots \ Prawidłowy\}}$

jest gęsty w przedziale (0,1).

Liczby totientne

Liczba totient jest wartością funkcji totient Eulera, to znaczy m , dla którego istnieje co najmniej jeden n , dla którego φ ( n ) = m . Wartościowością lub krotnością totientu m jest liczba rozwiązań tego równania . Nontotient to liczba naturalna , która nie jest liczbą totient. Każda nieparzysta liczba całkowita przekraczająca 1 jest trywialnie nontotientem. Istnieje również nieskończenie wiele parzystych nontotientów i rzeczywiście każda dodatnia liczba całkowita ma wielokrotność, która jest parzystym nontotiantem.

Liczba totientów do określonej granicy x wynosi

${\ Displaystyle {\ Frac {x} {\ log x}} e ^ {{\ duży (} C + o ( 1){\big )}(\log \log \log x)^{2}}}$

dla stałej C = 0,8178146... .

Jeśli liczyć zgodnie z krotnością, liczba totientów do danej granicy x wynosi

${\ Displaystyle {\ duży \ vert} \ {n: \ varphi (n) \ równoważnik x \} {\ duży \ vert} = {\frac {\zeta (2)\zeta (3)}{\zeta (6)}}\cdot x+R(x)}$

gdzie składnik błędu R jest rzędu co najwyżej x / (log x ) ^k dla dowolnego dodatniego k .

Wiadomo, że krotność m przekracza m ^δ nieskończenie często dla dowolnego δ < 0,55655 .

Twierdzenie Forda

Ford (1999) udowodnił, że dla każdej liczby całkowitej k ≥ 2 istnieje liczba totient m o krotności k : to znaczy dla której równanie φ ( n ) = m ma dokładnie k rozwiązań; wynik ten przypuszczał wcześniej Wacław Sierpiński , a uzyskano go w konsekwencji hipotezy Schinzela H. Rzeczywiście, każda wielość, która się pojawia, dzieje się tak nieskończenie często.

Jednak żadna liczba m nie jest znana z krotnością k = 1 . Hipoteza funkcji totient Carmichaela jest stwierdzeniem, że nie ma takiego m .

Doskonałe liczby totientów

Główny artykuł: Idealna liczba totientów

Doskonała liczba totientów to liczba całkowita równa sumie iterowanych totientów. Oznacza to, że stosujemy funkcję totient do liczby n , stosujemy ją ponownie do wynikowej totient i tak dalej, aż do osiągnięcia liczby 1, i dodajemy wynikową sekwencję liczb; jeśli suma jest równa n , to n jest doskonałą totientną liczbą.

Aplikacje

cyklotomia

Główny artykuł: konstruowalny wielokąt

W ostatniej części Disquisitiones Gauss udowadnia, że ​​n -gon foremny można zbudować za pomocą liniału i kompasu, jeśli φ ( n ) jest potęgą liczby 2. Jeśli n jest potęgą nieparzystej liczby pierwszej, wzór na totient mówi, że totient może być potęgą dwójki tylko wtedy, gdy n jest pierwszą potęgą, a n − 1 jest potęgą 2. Liczby pierwsze, które są o jeden większe niż potęga 2, nazywane są liczbami pierwszymi Fermata i tylko pięć jest znanych: 3, 5, 17, 257 i 65537. Fermat i Gauss wiedzieli o nich. Nikt nie był w stanie udowodnić, czy jest ich więcej.

Zatem regularny n -gon ma konstrukcję prostoliniowo-kompasową, jeśli n jest iloczynem różnych liczb pierwszych Fermata i dowolnej potęgi liczby 2. Kilka pierwszych takich n to

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (sekwencja A003401 w OEIS ) .

Twierdzenie o liczbach pierwszych dla postępów arytmetycznych

Główny artykuł: Twierdzenie o liczbach pierwszych § Twierdzenie o liczbach pierwszych dla postępów arytmetycznych

Kryptosystem RSA

Główny artykuł: RSA (algorytm)

Konfiguracja systemu RSA polega na wybraniu dużych liczb pierwszych p i q , obliczeniu n = pq i k = φ ( n ) oraz znalezieniu dwóch liczb e i d takich , że ed ≡ 1 ( mod k ) . Liczby n i e („klucz szyfrujący”) są udostępniane publicznie, a d („klucz deszyfrujący”) pozostaje prywatny.

Wiadomość reprezentowana przez liczbę całkowitą m , gdzie 0 < m < n , jest szyfrowana przez obliczenie S = m ^e (mod n ) .

Jest odszyfrowywany przez obliczenie t = S ^d (mod n ) . Twierdzenie Eulera można wykorzystać do pokazania, że ​​jeśli 0 < t < n , to t = m .

Bezpieczeństwo systemu RSA byłoby zagrożone, gdyby liczbę n można było skutecznie rozłożyć na czynniki lub gdyby φ ( n ) można było skutecznie obliczyć bez faktoryzacji n .

Nierozwiązane problemy

przypuszczenie Lehmera

Główny artykuł: problem totienta Lehmera

Jeśli p jest liczbą pierwszą, to φ ( p ) = p - 1 . W 1932 roku DH Lehmer zapytał, czy istnieją liczby złożone n takie, że φ ( n ) dzieli n − 1 . Żadne nie są znane.

W 1933 roku udowodnił, że jeśli takie n istnieje, to musi być nieparzyste, pozbawione kwadratów i podzielne przez co najmniej siedem liczb pierwszych (tj. ω ( n ) ≥ 7 ). W 1980 roku Cohen i Hagis udowodnili, że n > 10 ²⁰ i że ω ( n ) ≥ 14 . Ponadto Hagis wykazał, że jeśli 3 dzieli n , to n > 10 ^1937042 i ω ( n ) ≥ 298848 .

Przypuszczenie Carmichaela

Główny artykuł: hipoteza funkcji totient Carmichaela

Stwierdza to, że nie ma liczby n o takiej własności, jak dla wszystkich innych liczb m , m ≠ n , φ ( m ) ≠ φ ( n ) . Zobacz twierdzenie Forda powyżej.

Jak stwierdzono w głównym artykule, jeśli istnieje jeden kontrprzykład na to przypuszczenie, musi istnieć nieskończenie wiele kontrprzykładów, a najmniejszy z nich ma co najmniej dziesięć miliardów cyfr o podstawie 10.

Hipoteza Riemanna

Hipoteza Riemanna jest prawdziwa wtedy i tylko wtedy, gdy nierówność

${\ Displaystyle {\ Frac {n} {\ varphi (n)} <e ^ { \gamma }\log \log n+{\frac {e^{\gamma }(4+\gamma -\log 4\pi )}{\sqrt {\log n}}}}$

jest prawdziwe dla wszystkich n ≥ p ₁₂₀₅₆₉ # gdzie γ jest stałą Eulera , a p ₁₂₀₅₆₉ # jest iloczynem pierwszych 120569 liczb pierwszych.

Zobacz też

• Funkcja Carmichaela
• Hipoteza Duffina-Schaeffera
• Uogólnienia małego twierdzenia Fermata
• Wysoce złożona liczba
• Multiplikatywna grupa liczb całkowitych modulo n
• Suma Ramanujana
• Funkcja podsumowująca totient
• Funkcja psi Dedekinda

Notatki

Disquisitiones Arithmeticae został przetłumaczony z łaciny na angielski i niemiecki. Wydanie niemieckie zawiera wszystkie prace Gaussa dotyczące teorii liczb: wszystkie dowody wzajemności kwadratowej, wyznaczenie znaku sumy Gaussa, badania wzajemności dwukwadratowej oraz niepublikowane notatki.

Odniesienia do Disquisitiones mają formę Gauss, DA, art. nnn .

•   Abramowitz M. ; Stegun, IA (1964), Podręcznik funkcji matematycznych , Nowy Jork: Dover Publications , ISBN 0-486-61272-4 . Patrz paragraf 24.3.2.
•    Bacha, Erica ; Shallit, Jeffrey (1996), Algorytmiczna teoria liczb (tom I: wydajne algorytmy) , MIT Press Series in the Foundations of Computing , Cambridge, MA: The MIT Press , ISBN 0-262-02405-5 , Zbl 0873.11070
• Dickson, Leonard Eugene, „Historia teorii liczb”, tom 1, rozdział 5 „Funkcja Eulera, uogólnienia; seria Farey”, Chelsea Publishing 1952
•      Ford, Kevin (1999), „Liczba rozwiązań φ ( x ) = m ”, Annals of Mathematics , 150 (1): 283–311, doi : 10,2307/121103 , ISSN 0003-486X , JSTOR 121103 , MR 1715326 , Zbl 0978.11053 .
•   Gauss, Carl Friedrich (1986), Disquisitiones Arithmeticae (drugie, poprawione wydanie) , przekład Clarke, Arthur A., ​​New York: Springer , ISBN 0-387-96254-9
•   Gauss, Carl Friedrich (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae i inne artykuły z teorii liczb) (wydanie drugie) , przekład Maser, H., New York: Chelsea, ISBN 0-8284-0191-8
•    Graham, Ronald ; Knut, Donald ; Patashnik, Oren (1994), Matematyka konkretna : podstawa informatyki (wyd. 2), Reading, MA: Addison-Wesley, ISBN 0-201-55802-5 , Zbl 0836.00001
•    Guy, Richard K. (2004), Unsolved Problems in Number Theory , Problem Books in Mathematics (3rd ed.), New York, NY: Springer-Verlag , ISBN 0-387-20860-7 , Zbl 1058.11001
•   Hardy, GH ; Wright, EM (1979), Wprowadzenie do teorii liczb (wyd. Piąte), Oxford: Oxford University Press , ISBN 978-0-19-853171-5
•   Long, Calvin T. (1972), Podstawowe wprowadzenie do teorii liczb (wyd. 2), Lexington: DC Heath and Company , LCCN 77-171950
•   Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elementy teorii liczb , Englewood Cliffs: Prentice Hall , LCCN 77-81766
•    Ribenboim, Paulo (1996), The New Book of Prime Number Records (3rd ed.), New York: Springer , ISBN 0-387-94457-5 , Zbl 0856.11001
•   Sandifer, Charles (2007), Wczesna matematyka Leonharda Eulera , MAA, ISBN 978-0-88385-559-1
•    Sandor, József; Mitrinović, Dragoslav S.; Crstici, Borysław, wyd. (2006), Podręcznik teorii liczb I , Dordrecht: Springer-Verlag , s. 9–36, ISBN 1-4020-4215-9 , Zbl 1151.11300
•    Sandor, Jozsef; Crstici, Borysław (2004). Podręcznik teorii liczb II . Dordrecht: Kluwer Academic. s. 179 –327. ISBN 1-4020-2546-7 . Zbl 1079.11001 .
• Schramm, Wolfgang (2008), „Transformata Fouriera funkcji największego wspólnego dzielnika” , Electronic Journal of Combinatorial Number Theory , A50 (8 (1)) .

Linki zewnętrzne

• „Funkcja totienta” , Encyklopedia matematyki , EMS Press , 2001 [1994]
• Funkcja Phi Eulera i chińskie twierdzenie o resztach — dowód, że φ ( n ) jest multiplikatywne
• Kalkulator funkcji totient Eulera w JavaScript — do 20 cyfr
• Dineva, Rosica, Totient Eulera, Möbius i funkcje dzielnika
• Plytage, Loomis, Polhill Podsumowanie funkcji Eulera Phi