Gruby przedmiot (geometria)

W geometrii gruby obiekt to obiekt w dwóch lub więcej wymiarach, którego długości w różnych wymiarach są podobne. Na przykład kwadrat jest gruby, ponieważ jego długość i szerokość są identyczne. Prostokąt 2 na 1 jest cieńszy niż kwadrat, ale jest grubszy w porównaniu z prostokątem 10 na 1. Podobnie koło jest grubsze niż elipsa 1 na 10, a trójkąt równoboczny jest grubszy niż bardzo rozwarty trójkąt .

Grube obiekty są szczególnie ważne w geometrii obliczeniowej . Wiele algorytmów w geometrii obliczeniowej może działać znacznie lepiej, jeśli ich dane wejściowe składają się tylko z grubych obiektów; patrz aplikacji poniżej.

Globalna otyłość

Biorąc pod uwagę stałą R ≥ 1, obiekt o nazywany jest R -tłuszczem , jeśli jego „współczynnik smukłości” wynosi co najwyżej R . „Współczynnik szczupłości” ma różne definicje w różnych artykułach. Powszechna definicja to:

${\ Displaystyle {\ Frac {{\ tekst {bok najmniejszego sześcianu obejmujący}} \ o} {{\ tekst {bok największego sześcianu zawarty w}} \ o} }}$

gdzie o i sześciany są d -wymiarowe. Dwuwymiarowy sześcian to kwadrat , więc współczynnik grubości kwadratu wynosi 1 (ponieważ jego najmniejszy otaczający kwadrat jest taki sam, jak największy zamknięty dysk). Współczynnik smukłości prostokąta o wymiarach 10 na 1 wynosi 10. Współczynnik smukłości koła wynosi √2. Stąd, zgodnie z tą definicją, kwadrat jest 1-tłuszczowy, ale krążek i prostokąt 10 × 1 nie są 1-tłuszczowe. Kwadrat jest również 2-tłuszczowy (ponieważ jego współczynnik smukłości jest mniejszy niż 2), 3-tłuszczowy itp. Dysk jest również 2-tłuszczowy (a także 3-tłuszczowy itp.), Ale prostokąt 10 × 1 nie jest 2 -tłuszcz. Każdy kształt jest ∞-gruby, ponieważ z definicji współczynnik szczupłości wynosi zawsze co najwyżej ∞.

Powyższą definicję można nazwać otłuszczeniem dwóch kostek, ponieważ opiera się ona na stosunku długości boków dwóch kostek. Podobnie można zdefiniować dwukulowe , w którym zamiast tego używana jest kula d-wymiarowa . Kula dwuwymiarowa jest dyskiem . Zgodnie z tą alternatywną definicją dysk jest 1-tłuszczowy, ale kwadrat nie jest 1-tłuszczowy, ponieważ jego smukłość dwóch kul wynosi √ 2.

Alternatywna definicja, którą można nazwać grubością kuli otaczającej (zwaną także „grubością”), opiera się na następującym współczynniku smukłości:

${\ Displaystyle \ lewo ({\ Frac {{\ tekst {objętość najmniejszej otaczającej piłki}} \ o} {{\ tekst {objętość}} \ o} }\prawo)^{1/d}}$

Wykładnik 1/ d czyni tę definicję stosunkiem dwóch długości, tak że jest ona porównywalna z grubością dwóch kul.

Tutaj również zamiast piłki można użyć kostki.

Podobnie możliwe jest zdefiniowanie otłuszczenia kuli zamkniętej na podstawie następującego współczynnika smukłości:

${\ Displaystyle \ lewo ({\ Frac {{\ tekst {objętość}} \ o} {{\ tekst {objętość największej kuli zawartej w}} \ o}}\prawo)^{1/d}}$

Tłuszcz zamknięty vs. tłuszcz zamknięty

Szczupłość otaczającej kuli/sześcianu może bardzo różnić się od szczupłości zamkniętej kuli/sześcianu.

Weźmy na przykład lizaka z cukierkiem w kształcie kwadratu 1×1 i patykiem w kształcie prostokąta b ×(1/ b ) (gdzie b >1>(1/ b )). Wraz ze b zwiększa się pole otaczającego sześcianu (≈ b ² ), ale pole zamkniętego sześcianu pozostaje stałe (=1), a całkowita powierzchnia kształtu również pozostaje stała (=2). W ten sposób szczupłość sześcianu otaczającego może rosnąć dowolnie, podczas gdy szczupłość zamkniętego sześcianu pozostaje stała (= √ 2). Zobacz tę stronę GeoGebra , aby zobaczyć demonstrację.

Z drugiej strony, rozważmy prostoliniowego „węża” o szerokości 1/b i długości b , który jest całkowicie złożony w kwadracie o boku 1. Gdy b rośnie, pole zamkniętego sześcianu (≈1/ b ² ) maleje , ale całkowite pola węża i otaczającego go sześcianu pozostają stałe (=1). Zatem szczupłość zamkniętego sześcianu może rosnąć dowolnie, podczas gdy szczupłość otaczającego sześcianu pozostaje stała (= 1).

Zarówno w przypadku lizaka, jak i węża, szczupłość dwóch kostek rośnie dowolnie, ponieważ ogólnie:

otaczająca-kula-szczupłość ⋅ zamknięta-kula-szczupłość = dwie kule-szczupłość

otaczająca-sześcian-szczupłość ⋅ zamknięta-sześcian-szczupłość = dwie-sześciany-szczupłość

Ponieważ wszystkie współczynniki smukłości wynoszą co najmniej 1, wynika z tego, że jeśli obiekt o jest R-tłuszczowy zgodnie z definicją dwóch kul/sześcianów, to jest również R-tłuszczowy zgodnie z otaczającą-kulą/sześcianem i zamkniętą-kulą/sześcianem definicje (ale nie jest odwrotnie, jak pokazano powyżej).

Kulki kontra kostki

Objętość d - wymiarowej kuli o promieniu r wynosi : V $\ Displaystyle V_ {d} \ cdot r ^ {d}}$ , gdzie V _d jest stałą zależną od wymiaru:

${\ Displaystyle V_ {d} = {\ Frac {\ pi ^ {d/2}} {\ Gamma ({\ Frac {d} {2}} + 1)}}}$

D -wymiarowy sześcian o boku długości 2 a ma objętość (2 a ) ^d . Jest on zamknięty w d -wymiarowej kuli o promieniu a√d , której objętość wynosi V _d ( a√ d ) ^d . Stąd dla każdego d -wymiarowego obiektu:

szczupłość obejmująca piłkę ≤ szczupłość obejmująca sześcian ⋅ ${\ Displaystyle {V_ {d}} ^ {1/d} \ cdot {\ sqrt {d}}/2}$ .

Dla parzystych wymiarów ( re = 2 k ) współczynnik upraszcza się do: ${\ Displaystyle {\ sqrt {0,5 \ pi k}} / {{(k!)} ^ { 1/2k}}}$ . W szczególności dla kształtów dwuwymiarowych V ₂ = π i współczynnik wynosi: √(0,5 π)≈1,25, więc:

otaczająca-smukłość-dysku ≤ otaczająca-kwadratowa-szczupłość ⋅ 1,25

Z podobnych rozważań:

zamknięta-sześcian-szczupłość ≤ zamknięta-kula-szczupłość ⋅ ${\ Displaystyle {V_ {d}} ^ {1/d} \ cdot {\ sqrt {d}}/2}$

zamknięty- smukłość kwadratowa ≤ smukłość zamkniętego dysku ⋅ 1,25

D -wymiarowa kula o promieniu a jest zamknięta w d -wymiarowym sześcianie o boku długości 2 a . Stąd dla każdego d -wymiarowego obiektu:

szczupłość obejmująca sześcian ≤ szczupłość obejmująca piłkę ⋅ ${\ Displaystyle 2 / {V_ {d}} ^ {1 / d}}$

Dla parzystych wymiarów ( d = 2 k ) współczynnik upraszcza się do: ${\ Displaystyle 2/ {(k!)} ^ {1/2 k} / {\ sqrt {\ pi }}}$ . W szczególności dla kształtów dwuwymiarowych współczynnik ten wynosi: 2/√π≈1,13, więc:

otaczająca-kwadrat-szczupłość ≤ otaczająca-smukłość-dysku ⋅ 1,13

Z podobnych rozważań:

szczupłość zamkniętej kuli ≤ szczupłość zamkniętego sześcianu ⋅ ${\ Displaystyle 2 / {V_ {d}} ^ {1/d}}$

szczupłość zamkniętego dysku ≤ szczupłość zamkniętego kwadratu ⋅ 1,13

Mnożenie powyższych relacji daje następujące proste zależności:

szczupłość-dwóch kul ≤ szczupłość-dwóch kostek ⋅ √ d

szczupłość-dwóch kostek ≤ szczupłość-dwóch kul ⋅ √ d

Zatem obiekt R -tłuszczowy zgodnie z definicją dwóch kul lub dwóch sześcianów jest co najwyżej R √ d -tłuszczem zgodnie z definicją alternatywną.

Lokalne otłuszczenie

Wszystkie powyższe definicje są globalne w tym sensie, że nie dotyczą małych, cienkich obszarów, które są częścią dużego grubego obiektu.

Weźmy na przykład lizaka z cukierkiem w kształcie kwadratu 1×1 i patykiem w kształcie prostokąta 1×(1/ b ) (gdzie b >1>(1/ b )). Gdy b rośnie, pole otaczającego sześcianu (=4) i pole zamkniętego sześcianu (=1) pozostają stałe, podczas gdy całkowite pole kształtu zmienia się tylko nieznacznie (=1+1/b ) . Zatem wszystkie trzy współczynniki szczupłości są ograniczone: szczupłość-otaczającego sześcianu ≤2, szczupłość-obudowy-sześcianu ≤2, szczupłość-dwóch sześcianów=2. Tak więc według wszystkich definicji lizak jest 2-tłuszczowy. Jednak część patyczka lizaka oczywiście staje się cieńsza i cieńsza.

W niektórych zastosowaniach takie cienkie części są niedopuszczalne, dlatego bardziej odpowiednie może być miejscowe otłuszczenie oparte na lokalnym współczynniku smukłości. Dla każdego globalnego współczynnika smukłości istnieje możliwość zdefiniowania wersji lokalnej. Na przykład dla smukłości otaczającej kuli możliwe jest zdefiniowanie lokalnej kuli otaczającej obiektu o , biorąc pod uwagę zbiór B wszystkich piłek, których środek znajduje się wewnątrz o i których granica przecina granicę o ( tj. nie zawiera całkowicie o ). Lokalny współczynnik szczupłości kuli definiuje się jako:

${\ Displaystyle {\ Frac {1} {2}} \ cdot \ sup _ {b \ w B} \ lewo ({\ Frac {{\text{objętość}}\ B}{{\text{objętość}}\ B\cap o}}\right)^{1/d}}$

1/2 jest współczynnikiem normalizacji, który sprawia, że ​​lokalna-otaczająca-kula-szczupłość piłki jest równa 1. Lokalnie-otaczająca-kula-smukłość opisanego powyżej kształtu lizaka jest zdominowana przez 1×(1/ b ) trzyma się i przechodzi do ∞, gdy b rośnie. Zatem zgodnie z lokalną definicją powyższy lizak nie jest 2-tłuszczowy.

Definicje globalne a lokalne

Otłuszczenie lokalne implikuje otłuszczenie globalne. Oto szkic próbny dla otłuszczenia oparty na otaczających kulach. Z definicji objętość najmniejszej otaczającej kuli jest ≤ objętość dowolnej innej otaczającej kuli. W szczególności jest to ≤ objętość dowolnej otaczającej kuli, której środek znajduje się wewnątrz o i której brzeg styka się z brzegiem o . Ale każda taka otaczająca kula jest w zbiorze B rozważanym przez definicję szczupłości lokalnej kuli otaczającej. Stąd:

otaczająca-kula-szczupłość ^d =

= objętość(najmniejsza-obejmująca-kula)/objętość( o )

≤ objętość(obejmująca-kulę- b -w- B )/objętość( o )

= objętość(obejmująca-kulę- b -w- B )/objętość( b ∩ o )

≤ (2 lokalne-obejmujące-kulę-szczupłość) ^d

Stąd:

otaczająca-kula-szczupłość ≤ 2⋅lokalna-otaczająca-kula-szczupłość

W przypadku wypukłego ciała jest również odwrotnie: lokalna-tłustość implikuje globalną-tłustość. Dowód opiera się na następującym lemacie. Niech o będzie przedmiotem wypukłym. Niech P będzie punktem w o . Niech b i B będą dwiema kulami o środku w punkcie P takimi, że b jest mniejsze od B . Wtedy o przecina większą część b niż B , tj.:

${\ Displaystyle {\ Frac {{\ tekst {objętość}} \ (b \ cap o)} {{\ tekst {tom} }\ (b)}}\geq {\frac {{\text{tom}}\ (B\cap o)}{{\text{tom}}\ (B)}}}$

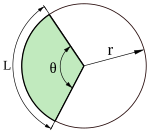
Szkic dowodowy: stojąc w punkcie P , możemy spojrzeć pod różnymi kątami θ i zmierzyć odległość do granicy o . Ponieważ o jest wypukłe, ta odległość jest funkcją, powiedzmy r ( θ ). Możemy obliczyć lewą stronę nierówności, całkując następującą funkcję (pomnożoną przez pewną funkcję wyznacznikową) dla wszystkich kątów:

${\ Displaystyle f (\ teta) = \ min {({\ Frac {r (\ teta)} {{\ tekst {promień}} \ (b)}},1)}}$

Podobnie możemy obliczyć prawą stronę nierówności, całkując następującą funkcję:

${\ Displaystyle F (\ teta) = \ min {({\ Frac {r (\ teta)} {{\ tekst {promień}} \ (B)}},1)}}$

Sprawdzając wszystkie 3 możliwe przypadki, można pokazać, że zawsze ${\ Displaystyle f (\ theta) \ geq F (\ theta)}$ . Zatem całka z f jest co najmniej całką z F i wynika z tego lemat.

Definicja szczupłości kul lokalnych obejmuje wszystkie kule, które są wyśrodkowane w punkcie w o i przecinają granicę o . Jednakże, gdy o jest wypukłe, powyższy lemat pozwala nam rozważać dla każdego punktu w o tylko kule o maksymalnym rozmiarze, tj. tylko kule, które w całości zawierają o (i których granica przecina granicę o ) . Dla każdej takiej kuli b :

${\ Displaystyle {\ tekst {objętość}} \ (b) \ równoważnik C_ {d} \ cdot {\ tekst {średnica}} \ (o) ^ {d$

gdzie $stałą$ zależną od wymiaru.

Średnica o jest co najwyżej średnicą najmniejszej kuli otaczającej o , a objętość tej kuli wynosi: ${\ Displaystyle C_ {d} \ cdot ({{ \text{średnica(najmniejsza otaczająca kulka}}\ o)/2)^{d}}$ . Połączenie wszystkich nierówności daje dla każdego wypukłego obiektu:

lokalna-otaczająca-kula-szczupłość ≤ otaczająca-kula-szczupłość

W przypadku obiektów niewypukłych ta nierówność oczywiście nie zachodzi, czego przykładem jest powyższy lizak.

Przykłady

Poniższa tabela przedstawia współczynnik smukłości różnych kształtów w oparciu o różne definicje. Dwie kolumny lokalnych definicji są wypełnione „*”, gdy kształt jest wypukły (w tym przypadku wartość lokalnej smukłości jest równa wartości odpowiedniej globalnej smukłości):

Kształt	dwie kule	dwa sześciany	otaczająca piłka	otaczający sześcian	zamknięta piłka	zamknięty sześcian	lokalna-otaczająca-piłka	lokalny-otaczający-sześcian
kwadrat	√2	1	√(π/2)≈1,25	1	√(4/π) ≈ 1,13	1	*	*
b × prostokąt z b > a	√(1+b^2/a^2)	b/a	0,5√π(a/b+b/a)	√ (b/a)	2√(b/aπ)	√ (b/a)	*	*
dysk	1	√2	1	√(4/π)≈1,13	1	√(π/2)≈1,25	*	*
elipsa o promieniach b > a	b / a	> b / a	√ ( b / za )	>√( b /2π za )	√ ( b / za )	>√(π b / a )	*	*
półelipsa o promieniach b > a , przepołowiona równolegle do b	2b / a _	>2 b / a	√(2 b / za )	>√(4 b /π za )	√(2 b / za )	>√(2π b / a )	*	*
półdysk	2	√5	√2	√(8/π)≈1,6	√2	√(5π/8)≈1,4	*	*
trójkąt równoboczny		1+2/√3≈2,15	√(π/√3)≈1,35	√(4/√3)≈1,52		√√3/2+1/√√3≈1,42	*	*
trójkąt prostokątny równoramienny	1/(√2-1)≈2,4	2		√2		√2	*	*
„lizak” złożony z kwadratu jednostkowego i b × patyczka , b >1> a		b +1		√(( b +1)^2/( ab +1))		√( ab +1)		√ (b/a)

Grubość trójkąta

Szczupłość jest niezmienna dla skali, więc współczynnik szczupłości trójkąta (podobnie jak każdego innego wielokąta) można przedstawić tylko jako funkcję jego kątów. Trzy współczynniki szczupłości oparte na piłce można obliczyć przy użyciu dobrze znanych tożsamości trygonometrycznych.

Szczupłość zamkniętej kuli

Największy okrąg zawarty w trójkącie nazywamy jego okręgiem . Wiadomo, że :

${\ Displaystyle \ Delta = r ^ {2} \ cdot (\ łóżeczko {\ Frac {\ kąt A} {2 }} + \ łóżeczko {\ frac {\ kąt B} {2}} + \ łóżeczko {\ frac {\ kąt C} {2}})}$

gdzie Δ to pole trójkąta, a r to promień okręgu. Stąd smukłość zamkniętej kuli trójkąta wynosi:

${\ Displaystyle {\ sqrt {\ Frac {\ łóżeczko {\ Frac {\ kąt A} {2}} + \ łóżeczko {\ Frac {\ kąt B}{2}}+\cot {\frac {\kąt C}{2}}}{\pi}}}}$

Szczupłość obejmująca kulę

Najmniejszym okręgiem zawierającym dla trójkąta ostrego jest jego okrąg , podczas gdy dla trójkąta rozwartego jest to okrąg, którego średnicą jest najdłuższy bok trójkąta.

Wiadomo, że :

${\ Displaystyle \ Delta = R ^ {2} \ cdot 2 \ sin A \ sin B \ sin C}$

gdzie ponownie Δ jest polem trójkąta, a R jest promieniem okręgu opisanego. Stąd dla trójkąta ostrego współczynnik smukłości otaczającej kuli wynosi:

${\ Displaystyle {\ sqrt {\ Frac {\ pi} {2 \ grzech A \ grzech B \ grzech C}}}}$

Wiadomo również, że:

${\ Displaystyle \ Delta = {\ Frac {c^{2}}{2(\cot \angle {A}+\cot \angle {B})}}={\frac {c^{2}(\sin \angle {A})(\sin \angle {B})}{2\sin(\angle {A}+\angle {B})}}}$

gdzie c jest dowolnym bokiem trójkąta, a A , B są sąsiednimi kątami. Stąd dla trójkąta rozwartokątnego o kątach ostrych A i B (oraz najdłuższym boku c ) współczynnik smukłości otaczającej kuli wynosi:

${\ Displaystyle {\ sqrt {\ Frac {\ pi \cdot (\cot \angle {A}+\cot \angle {B})}{2}}}={\sqrt {\frac {\pi \cdot \sin(\angle {A}+\angle { B})}{2(\sin \angle {A})(\sin \angle {B})}}}}$

, że w trójkącie prostokątnym ${\ Displaystyle \ sin {\ kąt {C}} = \ sin {\ kąt {A} + \ kąt {B}}$ , więc oba wyrażenia pokrywają się.

Szczupłość na dwie kulki

Promień wewnętrzny r i promień obwodowy R są połączone za pomocą kilku wzorów, które dostarczają dwóch alternatywnych wyrażeń dla smukłości dwóch kul trójkąta ostrego:

${\ Displaystyle {\ Frac {R}{r}}={\frac {1}{4\sin({\frac {\angle {A}}{2}})\sin({\frac {\angle {B}}{2} })\sin({\frac {\angle {C}}{2}})}}={\frac {1}{\cos \angle {A}+\cos \angle {B}+\cos \angle {C}-1}}}$

W przypadku trójkąta rozwartokątnego należy użyć c /2 zamiast R . Z prawa sinusów :

${\ Displaystyle {\ Frac {c} {2}} = R \ sin {\ kąt {C}}}$

Stąd współczynnik smukłości trójkąta rozwartokątnego o kącie rozwartym C wynosi:

${\ Displaystyle {\ Frac {c / 2} {r}} = {\ Frac {\ sin {\ kąt {C}}} {4 \ sin ({\ Frac {\ kąt {A}} {2} })\sin({\frac {\angle {B}}{2}})\sin({\frac {\angle {C}}{2}})}}={\frac {\sin {\angle {C}}}{\cos \angle {A}+\cos \angle {B}+\cos \angle {C}-1}}}$

$.$ , w trójkącie prostokątnym więc oba

Te dwa wyrażenia można połączyć w następujący sposób, aby uzyskać jedno wyrażenie na smukłość dwóch kul dowolnego trójkąta o mniejszych kątach A i B :

${\ Displaystyle {\ Frac {\ sin {\ max (\ kąt {A },\angle {B},\angle {C},\pi /2)}}{4\sin({\frac {\angle {A}}{2}})\sin({\frac {\angle {B}}{2}})\sin({\frac {\pi -\angle {A}-\angle {B}}{2}})}}={\frac {\sin {\max(\ kąt {A},\kąt {B},\kąt {C},\pi /2)}}{\cos \kąt {A}+\cos \kąt {B}-\cos(\kąt {A}+ \angle {B})-1}}}$

Aby poczuć tempo zmian otłuszczenia, rozważ, co daje ten wzór dla trójkąta równoramiennego o kącie główki θ , gdy θ jest małe :

${\ Displaystyle {\ Frac {\ sin {\ max(\theta ,\pi /2)}}{4\sin ^{2}({\frac {\pi -\theta}{4}})\sin({\frac {\theta}{2}} )}}\około {\frac {1}{4{\sqrt {1/2}}^{2}\theta /2}}={\frac {1}{\theta }}}$

Poniższe wykresy przedstawiają współczynnik smukłości trójkąta z dwoma kulkami:

• Szczupłość trójkąta ogólnego , gdy jeden kąt ( a ) jest stałym parametrem, a drugi kąt ( x ) się zmienia .
• Smukłość trójkąta równoramiennego jako funkcja kąta jego główki ( x ) .

Tłustość okręgów, elips i ich części

Kulkowa smukłość koła to oczywiście 1 - najmniejsza możliwa wartość.

W przypadku odcinka kołowego o kącie środkowym θ średnica okręgu opisanego jest długością cięciwy, a średnica okręgu jest wysokością odcinka, więc smukłość dwóch kul (i jej przybliżenie, gdy θ jest małe ) wynosi:

${\ Displaystyle {\ frac {\text{długość cięciwy}}{\text{wysokość odcinka}}}={\frac {2R\sin {\frac {\theta}}{2}}}{R\left(1-\cos { \frac {\theta }{2}}\right)}}={\frac {2\sin {\frac {\theta}}{2}}}{\left(1-\cos {\frac {\theta} {2}}\right)}}\około {\frac {\theta}}{\theta ^{2}/8}}={\frac {8}{\theta}}}$

W przypadku wycinka koła o kącie środkowym θ (gdy θ jest małe), średnica okręgu opisanego jest promieniem okręgu, a średnica okręgu jest długością cięciwy, więc smukłość dwóch kul wynosi:

${\ Displaystyle {\ Frac {\ tekst {promień okręgu}}} {\ tekst {długość akordu}}} = {\ Frac {R} {2R \ sin {\ Frac {\ teta }{2}}}} = {\ frac {1} {2} sin {\ frac {\ teta} {2} }}}\około {\frac {1}{2\theta /2}}={\frac {1}{\theta}}}$

W przypadku elipsy współczynniki smukłości są różne w różnych miejscach. Weźmy na przykład elipsę z krótką osią a i długą osią b . długość cięciwy waha się między ${\ Displaystyle 2a \ sin {\ Frac {\ theta} {2}}}$ na węższej stronie elipsy a ${\ Displaystyle 2b \ sin {\ frac {\ theta }{2}}}$ na jego szerszym boku; $_$ wysokość _ ${\ Displaystyle a \ lewo (1- \ sałata {\ Frac {\ theta} {2}} \ prawej)}$ na jego szerszym boku. Tak więc szczupłość dwóch kul waha się między:

${\ Displaystyle {\ Frac {2a \ sin {\ Frac {\ teta} {2}}} {b \ lewo (1- \ sałata {\frac {\theta}}{2}}\right)}}\około {\frac {8a}{b\theta}}}$

I:

${\ Displaystyle {\ Frac {2b \ sin {\ Frac {\ teta} {2}}} {a \ lewo (1- \ sałata {\frac {\theta}{2}}\right)}}\około {\frac {8b}{a\theta}}}$

Ogólnie rzecz biorąc, gdy sieczna zaczyna się pod kątem Θ, współczynnik smukłości można przybliżyć za pomocą:

${\ Displaystyle {\ Frac {2 \ sin {\ Frac {\ teta} {2}}} {\ lewo (1- \ sałata {\ Frac {\ teta} {2}} \ prawej)}}}$${\ Displaystyle \ lewo ({\ Frac {b} {a} }\cos ^{2}(\Theta +{\frac {\theta}{2}})+{\frac {a}{b}}\sin ^{2}(\Theta +{\frac {\theta }{2}})\prawo)}$

Grubość wypukłego wielokąta

Wielokąt wypukły nazywany jest r -rozdzielonym , jeśli kąt między każdą parą krawędzi (niekoniecznie sąsiadujących) wynosi co najmniej r .

Lemat: szczupłość otaczającej kulki wielokąta wypukłego oddzielonego od siebie wynosi co najwyżej ${\ Displaystyle O (1/r)}$ .

Wielokąt wypukły nazywamy k,r -rozdzielony, jeśli:

1. Nie ma równoległych krawędzi, może z wyjątkiem dwóch poziomych i dwóch pionowych.
2. Każda krawędź nierównoległa do osi tworzy kąt co najmniej r z dowolną inną krawędzią oraz z osiami x i y.
3. Jeśli istnieją dwie poziome krawędzie, to średnica/wysokość wynosi co najwyżej k .
4. Jeśli istnieją dwie pionowe krawędzie, to średnica/szerokość wynosi co najwyżej k .

Lemat: szczupłość otaczającej kulki wielokąta wypukłego oddzielonego k, r wynosi co najwyżej ${\ Displaystyle O (\ max (k, 1 / r))}$ . popraw górną granicę do ${\ Displaystyle O (d)}$ .

Liczenie grubych przedmiotów

Jeśli obiekt o V _d ad ^ma średnicę 2 a , to każda kula zawierająca o musi mieć promień co najmniej a i objętość co najmniej . Stąd, zgodnie z definicją tłustości obejmującej kulkę, objętość obiektu R o średnicy 2 a musi wynosić co najmniej: V _d a ^d / R ^d . Stąd:

Lemat 1 : Niech R ≥1 i C ≥0 będą dwiema stałymi. Rozważmy kolekcję nienakładających się d -wymiarowych obiektów, z których wszystkie są globalnie R -tłuste (tj. o smukłości obejmującej kulę ≤ R ). Liczba takich obiektów o średnicy co najmniej 2 a , zawartych w kuli o promieniu C⋅a , wynosi co najwyżej:

${\ Displaystyle V_ {d} \ cdot (Ca) ^ {d} / (V_ {d} \ cdot a ^ {d} / R ^ {d}) = (RC) ^ {d}}$

Na przykład (biorąc d = 2, R = 1 i C = 3): Liczba nienachodzących na siebie dysków o promieniu co najmniej 1 zawartych w okręgu o promieniu 3 wynosi co najwyżej 3 ² = 9. (W rzeczywistości jest to co najwyżej 7).

Jeśli weźmiemy pod uwagę lokalną tłustość zamiast globalnej tłustości, możemy otrzymać mocniejszy lemat:

Lemat 2 : Niech R ≥1 i C ≥0 będą dwiema stałymi. Rozważ zbiór nienakładających się d -wymiarowych obiektów, z których wszystkie są lokalnie R -tłuste (tj. mają lokalnie otaczającą-kulę-smukłość ≤ R ). Niech o będzie pojedynczym obiektem w tym zbiorze o średnicy 2 a . Wtedy liczba obiektów w zbiorze o średnicy większej niż 2 a leżących w odległości 2C⋅a od obiektu o wynosi co najwyżej:

${\ Displaystyle (4R \ cdot (C + 1 ))^{d}}$

Na przykład (biorąc d = 2, R = 1 i C = 0): liczba nienachodzących na siebie dysków o promieniu większym niż 1, które dotykają danego dysku jednostkowego, wynosi co najwyżej 4 ² = 16 (nie jest to ścisłe ograniczenie, ponieważ w tym przypadku łatwo jest udowodnić górną granicę 5).

Uogólnienia

Poniższe uogólnienia otłuszczenia badano dla obiektów dwuwymiarowych.

Trójkąt ∆ jest (β, δ)-trójkątem płaskiego obiektu o (0<β≤π/3, 0<δ< 1), jeśli ∆ ⊆ o , to każdy z kątów ∆ wynosi co najmniej β, oraz długość każdej z jego krawędzi wynosi co najmniej δ·średnica ( o ). Obiekt o na płaszczyźnie jest (β,δ)-pokryty , jeśli dla każdego punktu P ∈ o istnieje (β, δ)-trójkąt ∆ z o , który zawiera P.

Dla obiektów wypukłych te dwie definicje są równoważne w tym sensie, że jeśli o jest α-tłuszczem dla pewnej stałej α, to jest ono również pokryte (β,δ) dla odpowiednich stałych β i δ i odwrotnie. Jednak w przypadku obiektów niewypukłych definicja bycia grubym jest bardziej ogólna niż definicja bycia pokrytym (β, δ).

Aplikacje

Grube przedmioty są używane w różnych problemach, na przykład:

• Planowanie ruchu - planowanie ścieżki dla robota poruszającego się pośród przeszkód staje się łatwiejsze, gdy przeszkodami są grube przedmioty.
• Sprawiedliwe krojenie ciasta - dzielenie ciasta staje się trudniejsze, gdy kawałki muszą być grubymi przedmiotami. Wymóg ten jest powszechny, na przykład, gdy „ciastem” do podziału jest majątek ziemski.
• Więcej zastosowań można znaleźć w poniższych referencjach.